 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
練習問題27 極限 はさみうちの原理

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0\lt a\lt b$とする.
$\displaystyle \lim_{x\to\infty}(a^x+b^x)^{\frac{1}{x}}$を求めよ.
この動画を見る
$0\lt a\lt b$とする.
$\displaystyle \lim_{x\to\infty}(a^x+b^x)^{\frac{1}{x}}$を求めよ.
高校入試だけど3次方程式 動画内に誘導あり! 徳島文理(改)

単元:
#数学(中学生)#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
この動画を見る
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
数学「大学入試良問集」【8−1 三角関数の最大・最小】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$0 \leqq x \leqq 2\pi$のとき、関数
$y=\sin^2x+\sqrt{ 3 }\ \sin\ x\ \cos\ x-2\cos^2x$の最大値と最小値、および、そのときの$x$の値を求めよ。
(2)
点$(x,y)$が原点を中心とする半径1の円周上を動くとき、$xy(x+y-1)$の最大値と最小値を求めよ。
この動画を見る
次の問いに答えよ。
(1)
$0 \leqq x \leqq 2\pi$のとき、関数
$y=\sin^2x+\sqrt{ 3 }\ \sin\ x\ \cos\ x-2\cos^2x$の最大値と最小値、および、そのときの$x$の値を求めよ。
(2)
点$(x,y)$が原点を中心とする半径1の円周上を動くとき、$xy(x+y-1)$の最大値と最小値を求めよ。
方程式を解け。
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x^{2}}=2x^2$を解け
(x:実数)
この動画を見る
$2^{x^{2}}=2x^2$を解け
(x:実数)
福田のわかった数学〜高校3年生理系010〜極限(10)解けない漸化式の極限

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(10)
$a_1=2, a_{n+1}=\sqrt{a_n+30}$ のとき、
$\lim_{n \to \infty}a_n$ を調べよ。
この動画を見る
数学$\textrm{III}$ 極限(10)
$a_1=2, a_{n+1}=\sqrt{a_n+30}$ のとき、
$\lim_{n \to \infty}a_n$ を調べよ。
福田のわかった数学〜高校2年生016〜折れ線の長さの最小値

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 直線の方程式
2点$A(5,1),B(2,8)$と$x$軸上、$y$軸上に
それぞれ2点$P,Q$がある。
$AP+PQ+QB$を最小にする点$P,Q$は?
この動画を見る
数学$\textrm{II}$ 直線の方程式
2点$A(5,1),B(2,8)$と$x$軸上、$y$軸上に
それぞれ2点$P,Q$がある。
$AP+PQ+QB$を最小にする点$P,Q$は?
平方根の小数部分

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 2$の小数部分をaとする
$\sqrt{32}$の小数部分を$\sqrt{\quad}$を用いず、aを用いて表せ。
この動画を見る
$\sqrt 2$の小数部分をaとする
$\sqrt{32}$の小数部分を$\sqrt{\quad}$を用いず、aを用いて表せ。
20和歌山県教員採用試験(数学:3番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$S_1=3$
$S_{n+1}-5S_n=3・2^{n+1}-3$
一般項$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$S_1=3$
$S_{n+1}-5S_n=3・2^{n+1}-3$
一般項$a_n$を求めよ.
背景を見破れ!
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{1}{2!9!}+\dfrac{1}{3!8!}+\dfrac{1}{4!7!}+\dfrac{1}{5!6!}=\dfrac{n}{10!}$
$\displaystyle \sum_{k=1}^{6}\dfrac{1}{k!(13-k)!}=\dfrac{n}{12!}$
この動画を見る
これを解け.
$\dfrac{1}{2!9!}+\dfrac{1}{3!8!}+\dfrac{1}{4!7!}+\dfrac{1}{5!6!}=\dfrac{n}{10!}$
$\displaystyle \sum_{k=1}^{6}\dfrac{1}{k!(13-k)!}=\dfrac{n}{12!}$
数学ができる/できないを分ける、たった1つのポイント~これで偏差値84.9!【篠原好】

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
これで偏差値84.9!
「数学ができる/できないを分ける、たった1つのポイント」についてお話しています。
この動画を見る
これで偏差値84.9!
「数学ができる/できないを分ける、たった1つのポイント」についてお話しています。
整数問題 早稲田実業

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$c^2+4a^2+b^2 =65$を満たす正の整数a,b,cの組を求めよ。
早稲田実業学校
この動画を見る
$c^2+4a^2+b^2 =65$を満たす正の整数a,b,cの組を求めよ。
早稲田実業学校
福田のわかった数学〜高校1年生016〜絶対不等式(4)

単元:
#数Ⅰ#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対不等式(4)
$0 \leqq x \leqq 4$のある$x$について
$x^2-2ax+12a+3 \gt 0$
が成り立つような$a$の値の範囲は?
この動画を見る
数学$\textrm{I}$ 絶対不等式(4)
$0 \leqq x \leqq 4$のある$x$について
$x^2-2ax+12a+3 \gt 0$
が成り立つような$a$の値の範囲は?
20和歌山県教員採用試験(数学:5番 整数問題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$x^2-7x+5=0$の2つの解を$\alpha,\beta$とする.
$\alpha^n+\beta^n-7^n$は
5の倍数であることを示せ.
この動画を見る
$\boxed{5}$
$x^2-7x+5=0$の2つの解を$\alpha,\beta$とする.
$\alpha^n+\beta^n-7^n$は
5の倍数であることを示せ.
どっちがでかい?

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$\dfrac{10^{2019}+1}{10^{2020}+1}$ VS $\dfrac{10^{2020}+1}{10^{2021}+1}$
この動画を見る
どちらが大きいか?
$\dfrac{10^{2019}+1}{10^{2020}+1}$ VS $\dfrac{10^{2020}+1}{10^{2021}+1}$
算数オリンピック 角度 C
単元:
#算数(中学受験)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#その他#算数オリンピック
指導講師:
数学を数楽に
問題文全文(内容文):
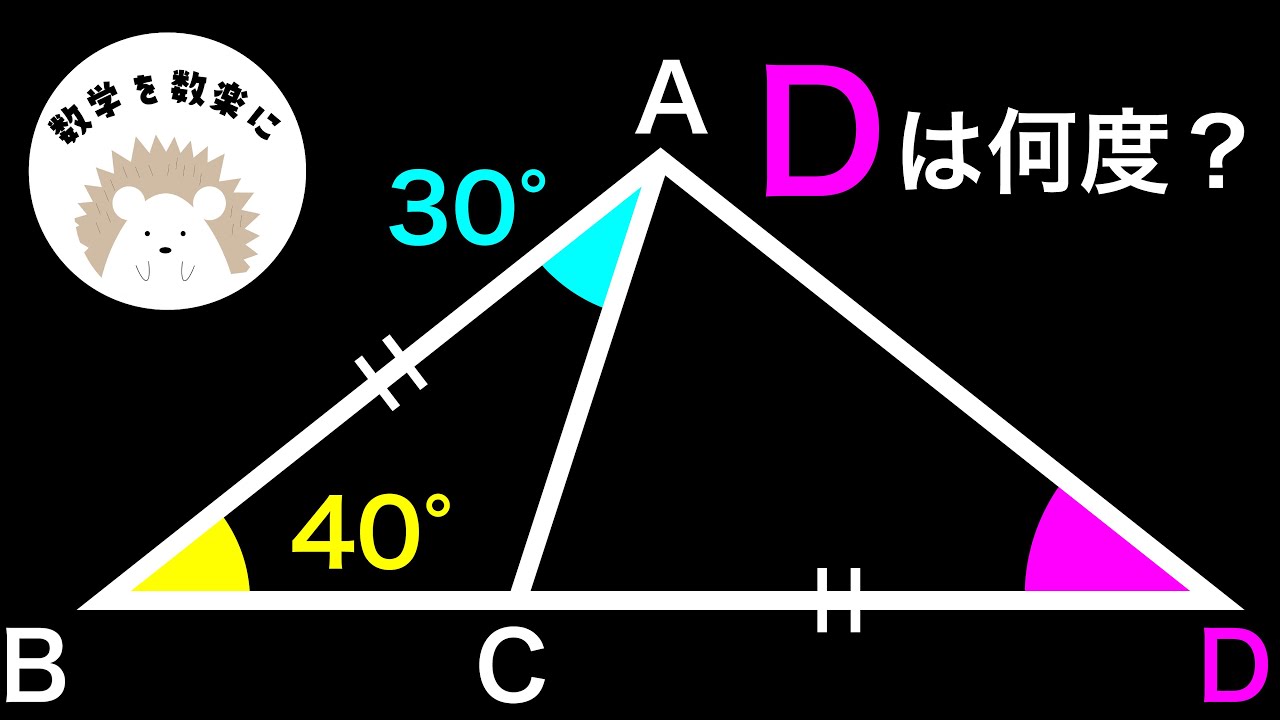
$\angle D=?$
*図は動画内参照
算数オリンピック
この動画を見る
$\angle D=?$
*図は動画内参照
算数オリンピック
数学「大学入試良問集」【7−6 正方形と長方形の共有面積】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
座標平面上に4点$O(0,0),A(2,0),B(2,1),C(0,1)$がある。
実数$a$に対して4点$P(a+1,a),Q(a,a+1),R(a-1,a),S(a,a-1)$をとる。
このとき、次の問いに答えよ。
(1)
長方形$QABC$と正方形$PQRS$が共有点をもつような$a$の範囲を求めよ。
(2)
長方形$OABC$と正方形$PQRS$の共通部分の面積が最大となる$a$の値と、そのときの共通部分の面積を求めよ。
この動画を見る
座標平面上に4点$O(0,0),A(2,0),B(2,1),C(0,1)$がある。
実数$a$に対して4点$P(a+1,a),Q(a,a+1),R(a-1,a),S(a,a-1)$をとる。
このとき、次の問いに答えよ。
(1)
長方形$QABC$と正方形$PQRS$が共有点をもつような$a$の範囲を求めよ。
(2)
長方形$OABC$と正方形$PQRS$の共通部分の面積が最大となる$a$の値と、そのときの共通部分の面積を求めよ。
京都大学大学院の合格法【ヨビノリとジャンケンで成功】

単元:
#その他#英語(高校生)#勉強法・その他#勉強法#勉強法#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
ポイズン松本さんとの対談動画です。
京都大学大学院に合格するための勉強法に迫ります!
受験の際の参考にしましょう!
この動画を見る
ポイズン松本さんとの対談動画です。
京都大学大学院に合格するための勉強法に迫ります!
受験の際の参考にしましょう!
【高校数学】1次不定方程式~どこよりも丁寧に教える~ 5-8【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1次不定方程式の分かりやすい解説動画です
この動画を見る
1次不定方程式の分かりやすい解説動画です
福田のわかった数学〜高校3年生理系009〜極限(9)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(9)
(1)$|x| \lt 1$のとき、$\lim_{n \to \infty}nx^n=0$を示せ。
(2)$\displaystyle \sum_{n=1}^{\infty}nx^{n-1}$の収束・発散を調べよ。
この動画を見る
数学$\textrm{III}$ 極限(9)
(1)$|x| \lt 1$のとき、$\lim_{n \to \infty}nx^n=0$を示せ。
(2)$\displaystyle \sum_{n=1}^{\infty}nx^{n-1}$の収束・発散を調べよ。
福田のわかった数学〜高校2年生015〜直線の方程式と内心

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 直線の方程式
$y=-\displaystyle \frac{3}{4}x+9, y=\displaystyle \frac{4}{3}x+9, $$y=\displaystyle \frac{3}{4}x-5$
で囲まれた三角形の内心の座標を求めよ。
この動画を見る
数学$\textrm{II}$ 直線の方程式
$y=-\displaystyle \frac{3}{4}x+9, y=\displaystyle \frac{4}{3}x+9, $$y=\displaystyle \frac{3}{4}x-5$
で囲まれた三角形の内心の座標を求めよ。
18和歌山県教員採用試験(数学:5番 定積分)

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$\displaystyle \int_{0}^{1}\dfrac{2x-1}{x^2+x+1}-dx$を解け.
この動画を見る
$\boxed{5}$
$\displaystyle \int_{0}^{1}\dfrac{2x-1}{x^2+x+1}-dx$を解け.
部分積分の基本 信州大

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\displaystyle \int_{}^{} e^{-x}\sin x dx$
信州大過去問
この動画を見る
これを解け.
$\displaystyle \int_{}^{} e^{-x}\sin x dx$
信州大過去問
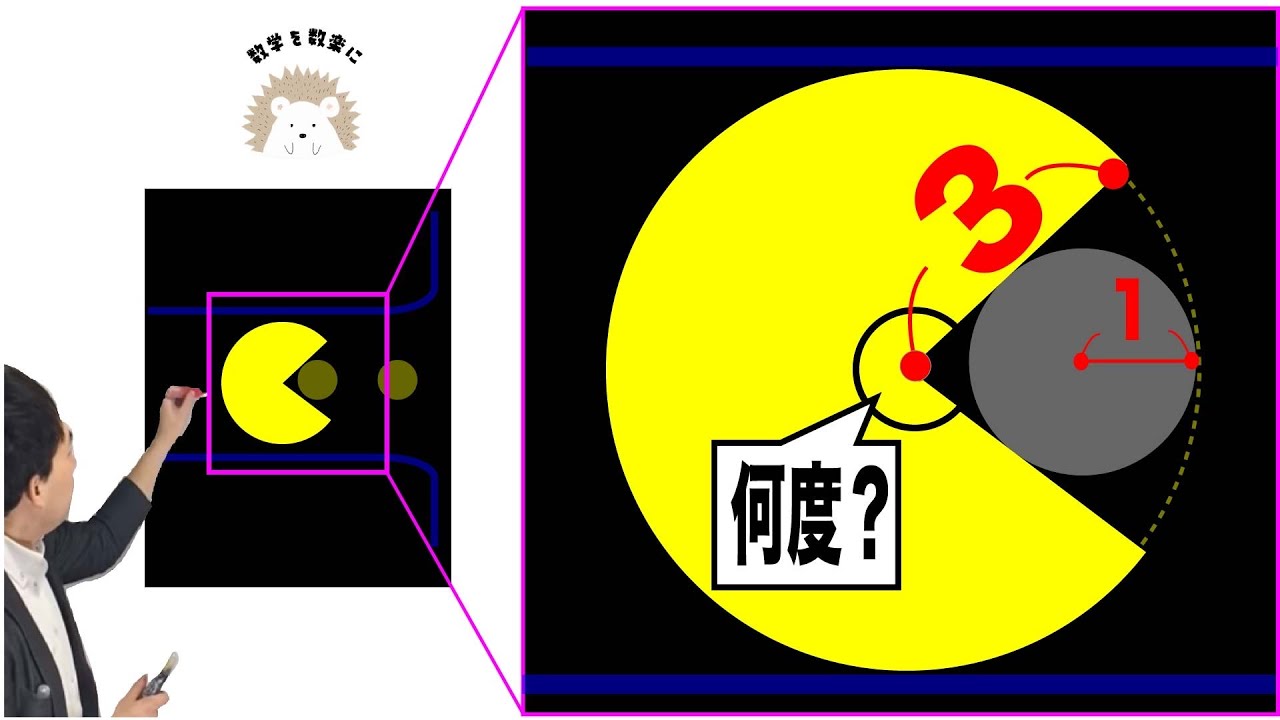
X=❓ パックマン再び
福田のわかった数学〜高校1年生015〜絶対不等式(3)

単元:
#数Ⅰ#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対不等式(3)
$0 \leqq x \leqq 4$ の全ての$x$について
$x^2-2ax+2a+3 \gt 0$
が成り立つような$a$の値の範囲は?
この動画を見る
数学$\textrm{I}$ 絶対不等式(3)
$0 \leqq x \leqq 4$ の全ての$x$について
$x^2-2ax+2a+3 \gt 0$
が成り立つような$a$の値の範囲は?
頭を柔らかく!動画内にヒントあり
練習問題25 2変数の最大値 教採 数検準1級
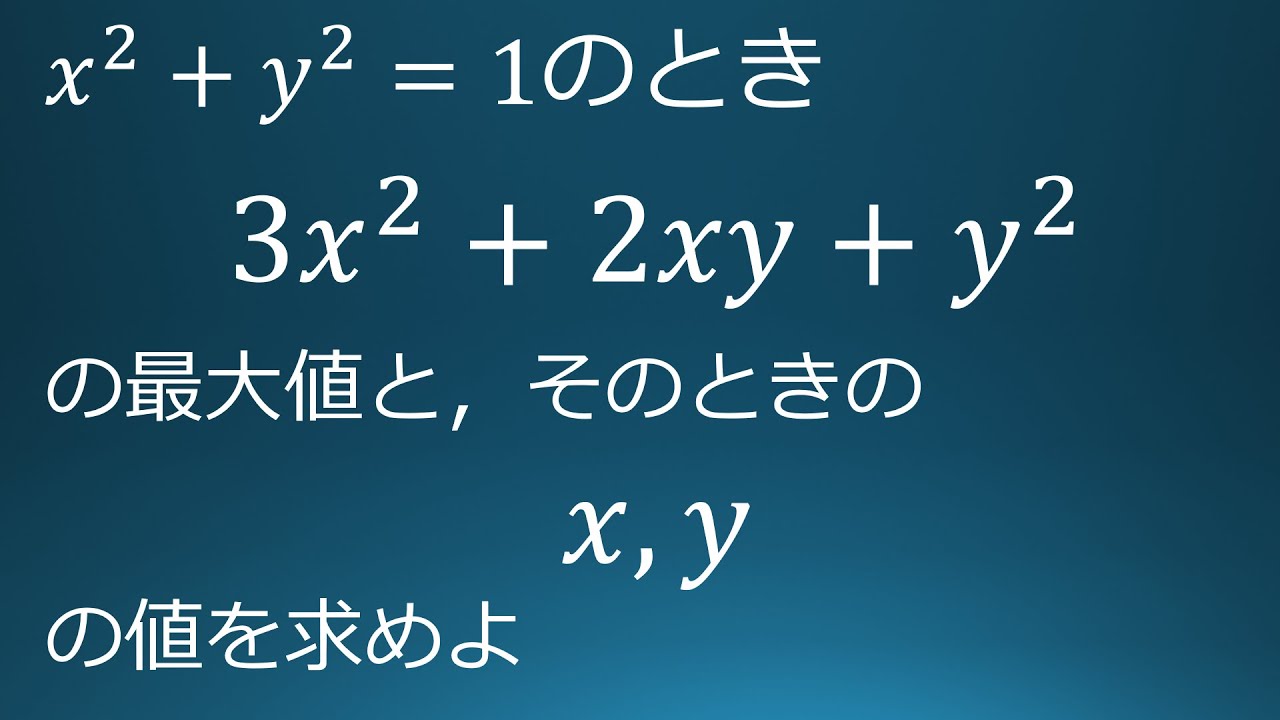
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#接線と増減表・最大値・最小値#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$x^2+y^2=1$のとき,
$3x^2+2xy+y^2$の最大値とそのときの
$x,y$の値を求めよ.
この動画を見る
$x^2+y^2=1$のとき,
$3x^2+2xy+y^2$の最大値とそのときの
$x,y$の値を求めよ.
6次式の因数分解 広島市立大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数の範囲で$x^6+1$を因数分解せよ.
2020広島市立大(類)過去問
この動画を見る
実数の範囲で$x^6+1$を因数分解せよ.
2020広島市立大(類)過去問
数学「大学入試良問集」【7−5 実数解と領域図示】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#大阪市立大学#大阪市立大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
実数$a,b$に対し、$x$についての2次方程式
$x^2-2ax+b=0$
は、$0 \leqq x \leqq 1$の範囲に少なくとも1つの実数解をもつとする。
このとき、$a,b$が満たす条件を求め、点$(a,b)$の存在する範囲を図示せよ。
この動画を見る
実数$a,b$に対し、$x$についての2次方程式
$x^2-2ax+b=0$
は、$0 \leqq x \leqq 1$の範囲に少なくとも1つの実数解をもつとする。
このとき、$a,b$が満たす条件を求め、点$(a,b)$の存在する範囲を図示せよ。
【裏ワザ?5分間!】二次関数:鹿児島県公立高等学校~全国入試問題解法【神授業】
単元:
#数学(中学生)#2次関数#高校入試過去問(数学)#鹿児島県公立高校入試#鹿児島県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
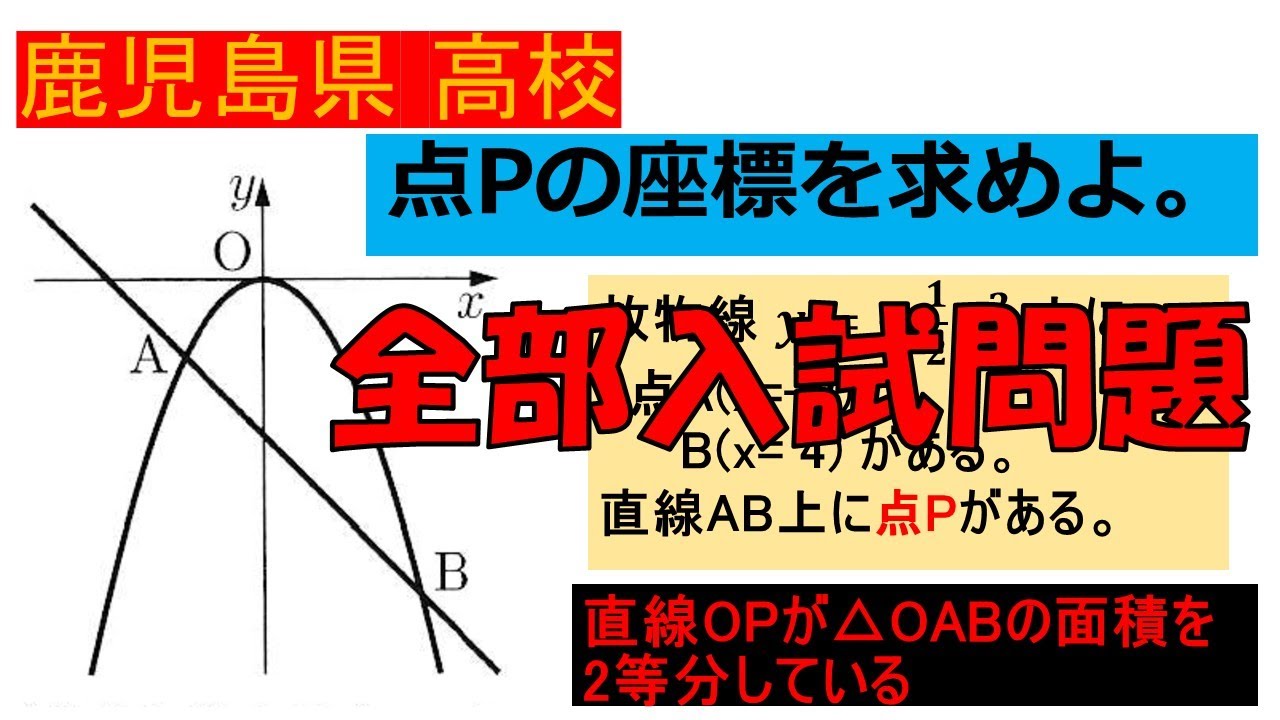
入試問題 鹿児島県の公立高等学校
点Pの座標を求めよ。
放物線 $y=\displaystyle \frac{1}{2}x^2$上に
2点$A(x=-2) B(x= 4)$がある。
直線$AB$上に点$P$がある。
直線$OP$が$\triangle OAB$の面積を 2等分している。
※図は動画内参照
この動画を見る
入試問題 鹿児島県の公立高等学校
点Pの座標を求めよ。
放物線 $y=\displaystyle \frac{1}{2}x^2$上に
2点$A(x=-2) B(x= 4)$がある。
直線$AB$上に点$P$がある。
直線$OP$が$\triangle OAB$の面積を 2等分している。
※図は動画内参照
福田のわかった数学〜高校3年生理系008〜極限(8)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(8)
自然数$N$は$n$桁の数とする。
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{\log_{10}N}{n}$を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(8)
自然数$N$は$n$桁の数とする。
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{\log_{10}N}{n}$を求めよ。
