 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅰ】中高一貫校問題集3(論理・確率編)19:集合と命題:命題と条件:必要条件、十分条件の見分け方

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
「x=2」ならば「x²=2x」であるための○○条件である 【集合と命題】【必要十分条件】
この動画を見る
「x=2」ならば「x²=2x」であるための○○条件である 【集合と命題】【必要十分条件】
数学「大学入試良問集」【2−6 相反方程式】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
実数$x \neq 0$に対して$|x+\displaystyle \frac{1}{x}|$のとり得る値の範囲を求めよ。
(2)
$a,b$を実数の定数とする。
方程式$x^4+ax^3+bx^2+ax+1=0$が実数解をもたないとき、点$(a,b)$の存在範囲を図示せよ。
この動画を見る
次の問いに答えよ。
(1)
実数$x \neq 0$に対して$|x+\displaystyle \frac{1}{x}|$のとり得る値の範囲を求めよ。
(2)
$a,b$を実数の定数とする。
方程式$x^4+ax^3+bx^2+ax+1=0$が実数解をもたないとき、点$(a,b)$の存在範囲を図示せよ。
07岡山県教員採用試験(数学:5番 行列)

単元:
#数Ⅱ#図形と方程式#円と方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$A=\begin{pmatrix}
p & 2 \\
-6 & -p-1
\end{pmatrix}$が
逆行列を持たないとする.$(p\gt 0)$
(1)$A^{2006}$を求めよ.
(2)一次変換$f=A$によって,楕円$\dfrac{x^2}{4}+y^2=1$を
うつした図形を求めよ.
この動画を見る
$\boxed{5}$
$A=\begin{pmatrix}
p & 2 \\
-6 & -p-1
\end{pmatrix}$が
逆行列を持たないとする.$(p\gt 0)$
(1)$A^{2006}$を求めよ.
(2)一次変換$f=A$によって,楕円$\dfrac{x^2}{4}+y^2=1$を
うつした図形を求めよ.
横浜市立(医)ド・モアブルと7倍角

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
この動画を見る
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
【なにこれ????】確率でよく出てくる言葉、解説します。【確率】【数学】

数学「大学入試良問集」【2−5 相加平均・相乗平均】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
以下の問いに答えよ。
(1)
正の実数$x,y$に対して
$\displaystyle \frac{y}{x}+\displaystyle \frac{x}{y} \geqq 2$
が成り立つことを示し、等号が成立するための条件を求めよ。
(2)
$n$を自然数とする。
$n$個の正の実数$a_1,a_2,・・・,a_n$に対して
$(a_1+・・・+a_n)\left[ \dfrac{ 1 }{ a_1 }+・・・+\displaystyle \frac{1}{a_n} \right] \geqq n^2$
が成り立つことを示し、等号が成立するための条件を求めよ。
この動画を見る
以下の問いに答えよ。
(1)
正の実数$x,y$に対して
$\displaystyle \frac{y}{x}+\displaystyle \frac{x}{y} \geqq 2$
が成り立つことを示し、等号が成立するための条件を求めよ。
(2)
$n$を自然数とする。
$n$個の正の実数$a_1,a_2,・・・,a_n$に対して
$(a_1+・・・+a_n)\left[ \dfrac{ 1 }{ a_1 }+・・・+\displaystyle \frac{1}{a_n} \right] \geqq n^2$
が成り立つことを示し、等号が成立するための条件を求めよ。
新高1生へ 失敗しないたすきがけ因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$48x^2+5x-18$
$(ax+b)(cx+d)$
この動画を見る
因数分解せよ.
$48x^2+5x-18$
$(ax+b)(cx+d)$
12岡山県教員採用試験(数学:1-6 微分方程式)

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(6)$
$f`(x)=x\sqrt{f(x)}$である.
$f(2)=1$を満たす関数$f(x)$を求めよ.
この動画を見る
$\boxed{1}-(6)$
$f`(x)=x\sqrt{f(x)}$である.
$f(2)=1$を満たす関数$f(x)$を求めよ.
【数Ⅲ】微分法の応用:接線と法線 関数 x²/2 + y²/8 =1 上の点P(1,2)における接線の方程式を求めよう。

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$\dfrac{x^2}{2}+\dfrac{y^2}{8}=1$上の点P(1,2)における接線の方程式を求めよう。
この動画を見る
曲線$\dfrac{x^2}{2}+\dfrac{y^2}{8}=1$上の点P(1,2)における接線の方程式を求めよう。
【数Ⅲ】微分法の応用:接線と法線 曲線 y=√x²+1 に点(1,0)から引いた接線と法線の方程式を求めよう。

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線 $y=\sqrt{x²+1}$ に点($1,0$)から引いた接線と法線の方程式を求めよう。
この動画を見る
曲線 $y=\sqrt{x²+1}$ に点($1,0$)から引いた接線と法線の方程式を求めよう。
【数Ⅲ】微分法の応用:接線と法線 媒介変数θで表された曲線について、( )内のθの値に対応する点における接線の方程式を求めよう。x=sinθ, y=sin2θ (θ=2π/3)

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
媒介変数$\theta$で表された曲線について、( )内の$\theta$の値に対応する点における接線の方程式を求めよう。
$x=\sin\theta, y=\sin2\theta (\theta=\dfrac{2\pi}{3})$
この動画を見る
媒介変数$\theta$で表された曲線について、( )内の$\theta$の値に対応する点における接線の方程式を求めよう。
$x=\sin\theta, y=\sin2\theta (\theta=\dfrac{2\pi}{3})$
【数Ⅲ】微分法の応用:接線と法線 関数 y=log(x-1) のグラフ上の点P(-2,0)における接線と法線の方程式を求めよう。

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数 $y=\log(x-1)$ のグラフ上の点P($-2,0$)における接線と法線の方程式を求めよう。
この動画を見る
関数 $y=\log(x-1)$ のグラフ上の点P($-2,0$)における接線と法線の方程式を求めよう。
【数Ⅲ】微分法の応用:接線と法線 放物線 y²=8x 上の点P(1,-2√2)における接線の方程式を求めよう。

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 $y^2=8x$ 上の点P($1,-2\sqrt2$)における接線の方程式を求めよう。
この動画を見る
放物線 $y^2=8x$ 上の点P($1,-2\sqrt2$)における接線の方程式を求めよう。
北海道大 微分積分

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4+6x^3-24x^2$の変曲点を$P(\alpha,f(\alpha)),Q(\beta,f(\beta))とする.(\alpha \gt \beta)$
$f(x)$の$P$における接線と$f(x)$で囲まれる面積を求めよ.
2021北海道大過去問
この動画を見る
$f(x)=x^4+6x^3-24x^2$の変曲点を$P(\alpha,f(\alpha)),Q(\beta,f(\beta))とする.(\alpha \gt \beta)$
$f(x)$の$P$における接線と$f(x)$で囲まれる面積を求めよ.
2021北海道大過去問
【数Ⅲ】微分法の応用:接線と法線 放物線 y²=8x 上の点P(1,-2√2)における接線の方程式を求めよう。

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y²=8x 上の点P(1,-2√2)における接線の方程式を求めよう。
この動画を見る
放物線 y²=8x 上の点P(1,-2√2)における接線の方程式を求めよう。
トーナメント表の対戦の組み合わせ (勝ち上がりの対戦は考慮しません!!)B

単元:
#数学(中学生)#数A#場合の数と確率#場合の数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A,B,C,D,Eの5チームがトーナメント表をもとに対戦する組み合わせは何通り?
*図は動画内参照
この動画を見る
A,B,C,D,Eの5チームがトーナメント表をもとに対戦する組み合わせは何通り?
*図は動画内参照
【知らなきゃ損!!】因数分解の応用例。これすぐ解けますか?【高校数学】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
以下を因数分解してください
$(2x-1)^2-(2x-1)-2$
この動画を見る
以下を因数分解してください
$(2x-1)^2-(2x-1)-2$
数学「大学入試良問集」【2−4 剰余の定理•商と余り】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の問いに答えよ。
(1)
$x$の整式$p(x)$を$x-3$で割った余りは$2,(x-2)^2$で割った余りは$x+1$である。
$p(x)$を$(x-2)^2$で割った商は$q(x)$とするとき、$q(x)$を$x-3$で割った余りを求めよ。
(2)
$p(x)$は(1)と同じ条件を満たすものとする。
このとき、$xp(x)$を$(x-3)(x-2)^2$で割った余りを求めよ。
この動画を見る
次の問いに答えよ。
(1)
$x$の整式$p(x)$を$x-3$で割った余りは$2,(x-2)^2$で割った余りは$x+1$である。
$p(x)$を$(x-2)^2$で割った商は$q(x)$とするとき、$q(x)$を$x-3$で割った余りを求めよ。
(2)
$p(x)$は(1)と同じ条件を満たすものとする。
このとき、$xp(x)$を$(x-3)(x-2)^2$で割った余りを求めよ。
兵庫県教員採用試験(数学練習問題1 y軸回転体)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$n$を自然数とする.
$y=\sin nx,y=1,y$軸で囲まれた部分を
$y$軸を中心に回転した体積$V$を求めよ.
この動画を見る
$n$を自然数とする.
$y=\sin nx,y=1,y$軸で囲まれた部分を
$y$軸を中心に回転した体積$V$を求めよ.
【数Ⅰ】2次関数:放物線とx軸との交点の位置 その1+その2

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学Ⅰ 二次関数】
$y=x^2+mx+2$が次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)このグラフとx軸の正の部分が異なる2点で交わる。
(2)グラフとx軸のx<-1の部分が異なる2点で交わる。
この動画を見る
【高校数学 数学Ⅰ 二次関数】
$y=x^2+mx+2$が次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)このグラフとx軸の正の部分が異なる2点で交わる。
(2)グラフとx軸のx<-1の部分が異なる2点で交わる。
札幌医科大2021 三角関数 複数解法

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\triangle ABC$で$\sin C=2\cos A\sin B$である.
$\triangle ABC$の形を求めよ.
2021札幌医大過去問
この動画を見る
$\triangle ABC$で$\sin C=2\cos A\sin B$である.
$\triangle ABC$の形を求めよ.
2021札幌医大過去問
【中学数学・数C】1次関数・平面ベクトル:座標平面上の三角形の面積

単元:
#数学(中学生)#中2数学#平面上のベクトル#1次関数#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は?
この動画を見る
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は?
たすきがけは、もう焦らない。これ見たらカンペキです【高校数学】

数学「大学入試良問集」【2−3 方程式と整数解】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#愛媛大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$p,q$を整数とし、$f(x)=x^2+px+q$とおく。
(1)
有理数$a$が方程式$f(x)=0$の一つの解ならば、$a$は整数であることを示せ。
(2)
$f(1)$も$f(2)$も$2$で割り切れないとき、方程式$f(x)=0$は整数の解を持たないことを示せ。
この動画を見る
$p,q$を整数とし、$f(x)=x^2+px+q$とおく。
(1)
有理数$a$が方程式$f(x)=0$の一つの解ならば、$a$は整数であることを示せ。
(2)
$f(1)$も$f(2)$も$2$で割り切れないとき、方程式$f(x)=0$は整数の解を持たないことを示せ。
【数B】数列:Σ計算、公式暗記の「前」に、「意味」を理解しよう!

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \sum_{k=1}^{n}(2k+3)$の値を求めなさい。
$\displaystyle \sum_{k=3}^{10}(k^2)$の値を求めなさい。
この動画を見る
$\displaystyle \sum_{k=1}^{n}(2k+3)$の値を求めなさい。
$\displaystyle \sum_{k=3}^{10}(k^2)$の値を求めなさい。
複素関数論⑭ 高専数学*5(1)(2) 複素積分の性質
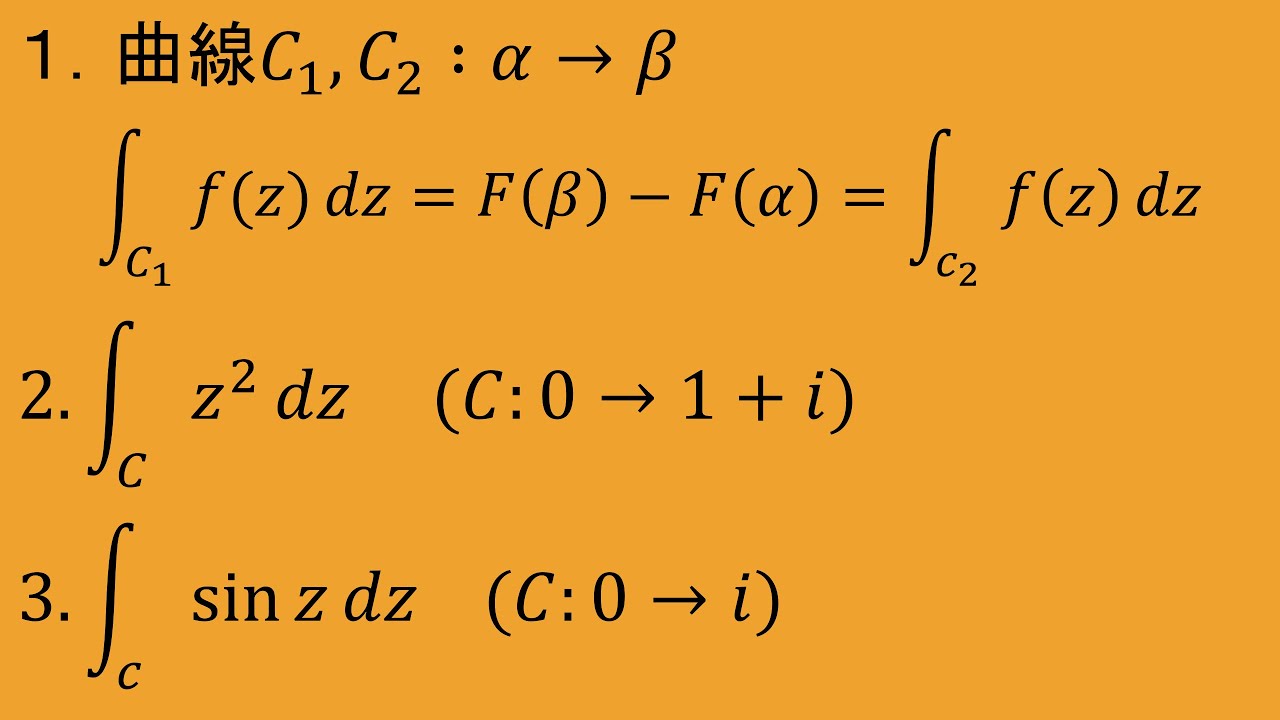
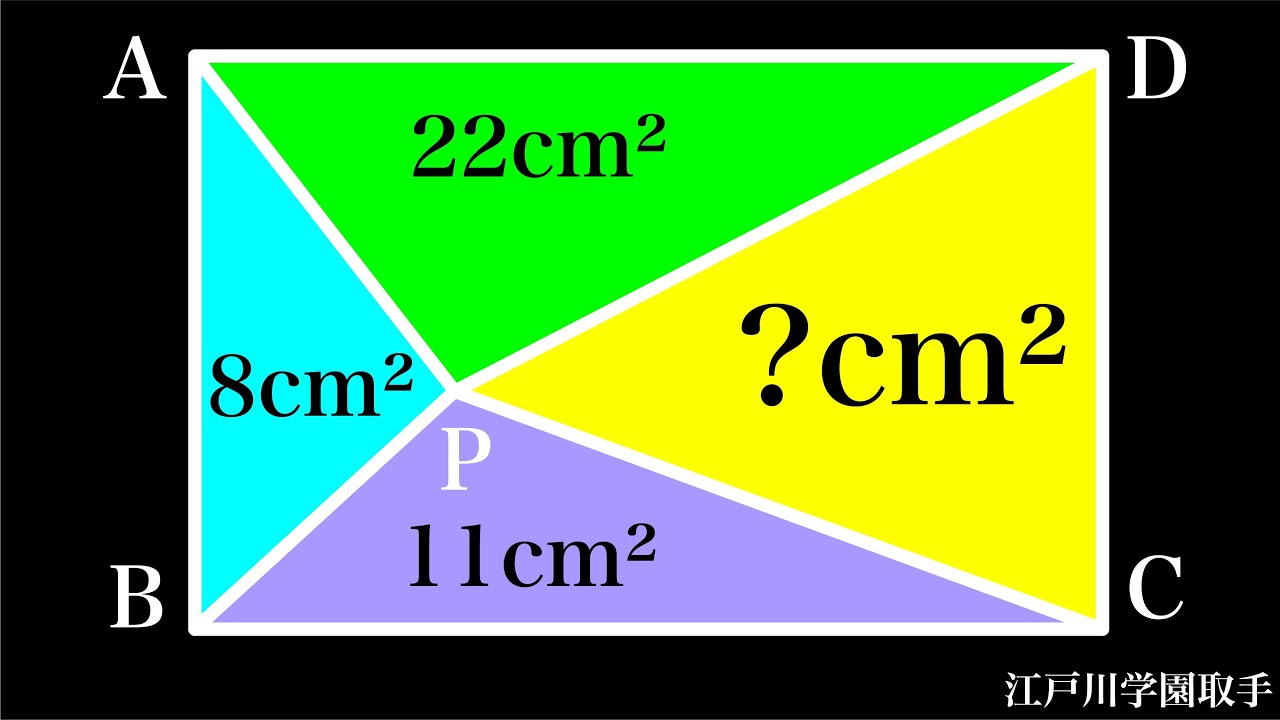
長方形の分割 江戸川学園取手
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
三角形CDPの面積=?
*図は動画内参照
この動画を見る
三角形CDPの面積=?
*図は動画内参照
03兵庫県教員採用試験(数学:5番 交点の個数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$0\lt a\neq 1$とする.
$y=x$と$y-\log_a x$の
交点の個数を調べよ.
この動画を見る
$\boxed{5}$
$0\lt a\neq 1$とする.
$y=x$と$y-\log_a x$の
交点の個数を調べよ.
札幌医科大学2021 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$n$に対し$N=(n+2)^3-n(n+1)(n+2)$が$36$の倍数になるような$n$をすべて求めよ.
2021札幌医大過去問
この動画を見る
自然数$n$に対し$N=(n+2)^3-n(n+1)(n+2)$が$36$の倍数になるような$n$をすべて求めよ.
2021札幌医大過去問
良問!!整数問題
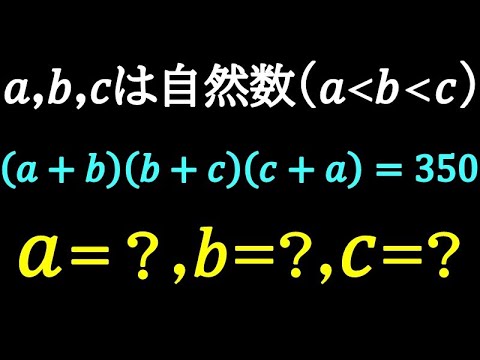
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a=? b=? c=?
a,b,cは自然数でa<b<c
(a+b)(b+c)(c+a)=350
この動画を見る
a=? b=? c=?
a,b,cは自然数でa<b<c
(a+b)(b+c)(c+a)=350
