 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
北海道大 整数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^2+n+14$が平方数となるような$n$(自然数)をすべて求めよ
出典:北海道大学 過去問
この動画を見る
$n^2+n+14$が平方数となるような$n$(自然数)をすべて求めよ
出典:北海道大学 過去問
中央大(法)ガウス記号 対数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[log_2(x+50)]=[log_2x]+3$を満たす$x$の範囲を求めよ
出典:2015年中央大学法学部 過去問
この動画を見る
$[log_2(x+50)]=[log_2x]+3$を満たす$x$の範囲を求めよ
出典:2015年中央大学法学部 過去問
順列と組合せを組み合わせてみました

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
5人の中から3人を選ぶ。
(1)全部で何通り?
(2)横1列に並べるとき何通り?
この動画を見る
5人の中から3人を選ぶ。
(1)全部で何通り?
(2)横1列に並べるとき何通り?
【裏技】ベクトルと面積比、これ知らない奴来い!
数列の和
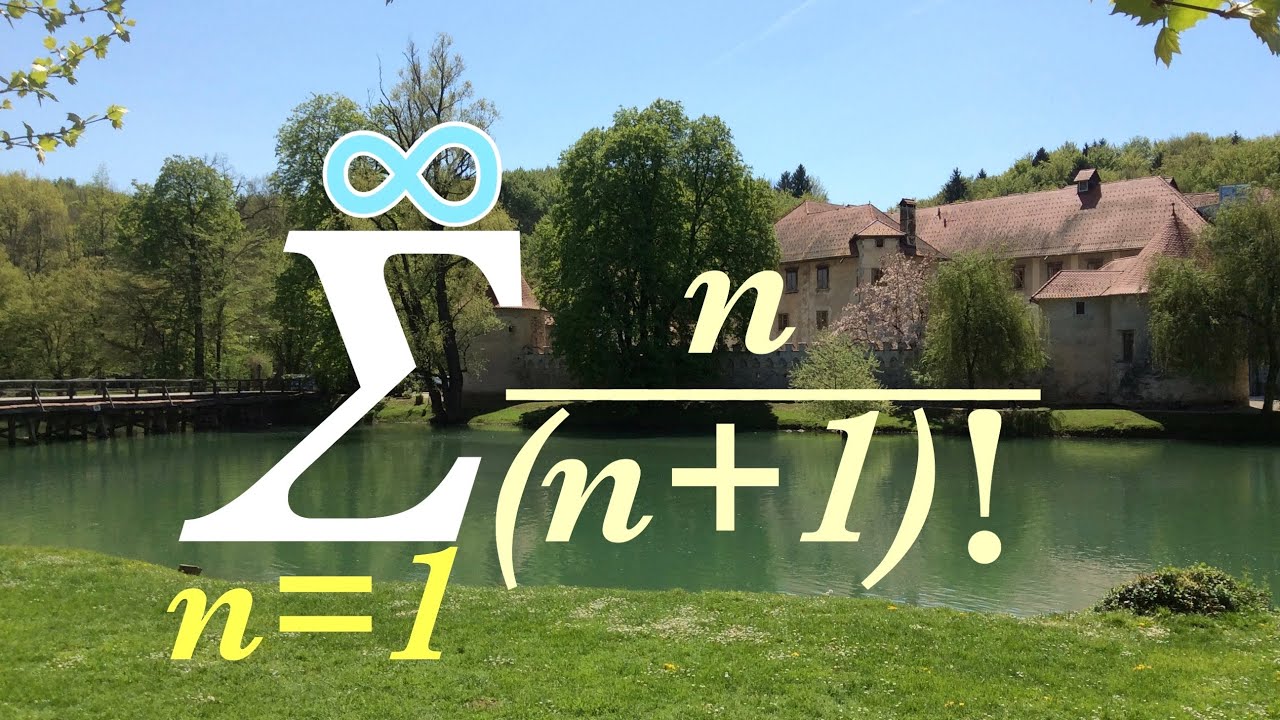
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{n}{(n+1)!}$
この動画を見る
$\displaystyle \sum_{n=1}^\infty \displaystyle \frac{n}{(n+1)!}$
福井大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
一般項を求めよ$(n$自然数$)$
$a_1=1$
$a_{n+1}=\displaystyle \frac{3}{n}S_n$
出典:福井大学 過去問
この動画を見る
一般項を求めよ$(n$自然数$)$
$a_1=1$
$a_{n+1}=\displaystyle \frac{3}{n}S_n$
出典:福井大学 過去問
2019 都立共通問題の最後の一問

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)#東京都立大学
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、$\textrm{R-APQ}$の体積は?
出典:東京都立大学
この動画を見る
動画内の図を参照し、$\textrm{R-APQ}$の体積は?
出典:東京都立大学
ゆく年くる年問題 2019~2020

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(2019+2020)(2019^2+2020^2)(2019^4+2020^4)$
$\times(2019^8+2020^8)(2019^{16}+2020^{16})$
$(2019^{32}+2020^{32})=2020^x-2019^x$
これを解け.
この動画を見る
$(2019+2020)(2019^2+2020^2)(2019^4+2020^4)$
$\times(2019^8+2020^8)(2019^{16}+2020^{16})$
$(2019^{32}+2020^{32})=2020^x-2019^x$
これを解け.
【数学B】漸化式6パターンを20分でまとめてみた!【まとめ動画】

横浜国大 複雑な漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_0=1$一般項を求めよ$(n$自然数$)$
$a_n=\displaystyle \sum_{k=1}^n 3^ka_{n-k}$
出典:2000年横浜国立大学 過去問
この動画を見る
$a_0=1$一般項を求めよ$(n$自然数$)$
$a_n=\displaystyle \sum_{k=1}^n 3^ka_{n-k}$
出典:2000年横浜国立大学 過去問
【特性方程式】どういう意味?←解説します
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$a_{n}=1,a_{n+1}=2a_{n}-3$のように定義される数列の一般項$a_{n}$は?
この動画を見る
$a_{n}=1,a_{n+1}=2a_{n}-3$のように定義される数列の一般項$a_{n}$は?
1の虚数3乗根ω(数II)

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1の虚数3乗根$\omega$についての解説動画です
以下を求めよ
(1)$\omega^{99}=?$
(2)$\omega^6+\omega^5+\omega^4=?$
この動画を見る
1の虚数3乗根$\omega$についての解説動画です
以下を求めよ
(1)$\omega^{99}=?$
(2)$\omega^6+\omega^5+\omega^4=?$
東工大 整数問題 合同式

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=19^n+(-1)^{n-1}2^{4n-3}$のすべてを割り切る素数を求めよ。
$(n$自然数$)$
出典:1986年東京工業大学 過去問
この動画を見る
$a_n=19^n+(-1)^{n-1}2^{4n-3}$のすべてを割り切る素数を求めよ。
$(n$自然数$)$
出典:1986年東京工業大学 過去問
【数学】ベクトル内積の成分表示ってどうしてこうなるの?

共通テストの記述が無くなる件について~高2生以下必見【篠原好】

単元:
#センター試験・共通テスト関連#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
高2生以下必見!
「共通テストの国語・数学の記述が無くなる件」についてお話しています。
この動画を見る
高2生以下必見!
「共通テストの国語・数学の記述が無くなる件」についてお話しています。
福岡教育大 連立漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2,b_1=1$
$a_{n+1}=a_n-8b_n$
$b_{n+1}=a_n+7b_n$
出典:1989年福岡教育大学 過去問
この動画を見る
$a_1=2,b_1=1$
$a_{n+1}=a_n-8b_n$
$b_{n+1}=a_n+7b_n$
出典:1989年福岡教育大学 過去問
鳴門教育大 2直線のなす角

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3$上の異なる2点$(a,a^3),(b,b^3)$における接線のなす角が$60^{ \circ }$である。
$a$と$b$の関係を式で表せ
出典:鳴門教育大学 過去問
この動画を見る
$y=x^3$上の異なる2点$(a,a^3),(b,b^3)$における接線のなす角が$60^{ \circ }$である。
$a$と$b$の関係を式で表せ
出典:鳴門教育大学 過去問
【高校数学】データの分析(分散、共分散など)

【数学A】外心・内心・チェバとかが誰でも嫌でも頭に入る動画
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学A】外心・内心・チェバなど 解説動画です
この動画を見る
【数学A】外心・内心・チェバなど 解説動画です
東京都立大

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z^4-2(\cos\displaystyle \frac{3}{7}\pi)z^3+2z^2-2(\cos\displaystyle \frac{3}{7}\pi)z+1=0$
(1)
$z+\displaystyle \frac{1}{z}$の値を求めよ
(2)
$z^n+\displaystyle \frac{1}{z^n}$の実部の最大値とそれを与える自然数$n$を求めよ
出典:東京都立大学 過去問
この動画を見る
$z^4-2(\cos\displaystyle \frac{3}{7}\pi)z^3+2z^2-2(\cos\displaystyle \frac{3}{7}\pi)z+1=0$
(1)
$z+\displaystyle \frac{1}{z}$の値を求めよ
(2)
$z^n+\displaystyle \frac{1}{z^n}$の実部の最大値とそれを与える自然数$n$を求めよ
出典:東京都立大学 過去問
【数学】点と直線の距離 公式の覚え方・導出

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学】点と直線の距離 公式の覚え方・導出の解説動画です
この動画を見る
【数学】点と直線の距離 公式の覚え方・導出の解説動画です
中央大(法)正多角形の内角

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1つの内角の比が$4:5$となる正多角形の組を求めよ
出典:2001年中央大学法学部 過去問
この動画を見る
1つの内角の比が$4:5$となる正多角形の組を求めよ
出典:2001年中央大学法学部 過去問
指数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
以下を解け
$9^x+15^x=25^x$
この動画を見る
以下を解け
$9^x+15^x=25^x$
成城大 ド・モアブル証明 6倍角の公式?

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#式と証明#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\cos\theta+i\sin\theta$
(1)
$n$整数
$z^n=\cos n \theta + i \sin n \theta$を示せ
(2)
$z+\displaystyle \frac{1}{z}$を$\cos \theta$を用いて表せ
(3)
$\cos^6\theta$を$\cos2\theta,\cos4\theta,\cos6\theta$を用いて表せ
出典:2005年成城大学 過去問
この動画を見る
$z=\cos\theta+i\sin\theta$
(1)
$n$整数
$z^n=\cos n \theta + i \sin n \theta$を示せ
(2)
$z+\displaystyle \frac{1}{z}$を$\cos \theta$を用いて表せ
(3)
$\cos^6\theta$を$\cos2\theta,\cos4\theta,\cos6\theta$を用いて表せ
出典:2005年成城大学 過去問
【合格体験記】宅浪で電通大に合格したFくん&シノハラの戦略立案の話【篠原好】
単元:
#その他#勉強法#その他#電気通信大学
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
「宅浪で電通大に合格したFくんの合格体験記と篠原先生の戦略立案」についてお話しています。
この動画を見る
「宅浪で電通大に合格したFくんの合格体験記と篠原先生の戦略立案」についてお話しています。
マイクロソフトの数学部で講師をしてきた。合同式で暗号

高次方程式を解く!その1(3次方程式4次方程式)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
高次方程式を解け。
(1)$x^3=1$
(2)$x^4=4$
(3)$x^4-3x^2-10=0$
この動画を見る
高次方程式を解け。
(1)$x^3=1$
(2)$x^4=4$
(3)$x^4-3x^2-10=0$
芝浦工業大 漸化式 特性方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#漸化式#学校別大学入試過去問解説(数学)#芝浦工業大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=9$
$S_{n+1}=4a_n-10$
一般項$a_n$を求めよ
出典:2005年芝浦工業大学 過去問
この動画を見る
$a_1=9$
$S_{n+1}=4a_n-10$
一般項$a_n$を求めよ
出典:2005年芝浦工業大学 過去問
【数学II】加法定理の証明の仕方を理解して覚える動画!

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学II】加法定理の証明についての説明動画です
この動画を見る
【数学II】加法定理の証明についての説明動画です
部分分数分解を利用した数列の和(数B)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$\displaystyle \frac{1}{1・2}+\displaystyle \frac{1}{2・3}+\displaystyle \frac{1}{3・4}+…+\displaystyle \frac{1}{n(n+1)}=??$
$\displaystyle \frac{1}{1・3}+\displaystyle \frac{1}{3・5}+\displaystyle \frac{1}{5・7}+…+\displaystyle \frac{1}{(2n-1)(2n+1)}=??$
この動画を見る
以下を求めよ。
$\displaystyle \frac{1}{1・2}+\displaystyle \frac{1}{2・3}+\displaystyle \frac{1}{3・4}+…+\displaystyle \frac{1}{n(n+1)}=??$
$\displaystyle \frac{1}{1・3}+\displaystyle \frac{1}{3・5}+\displaystyle \frac{1}{5・7}+…+\displaystyle \frac{1}{(2n-1)(2n+1)}=??$
