 平面図形
平面図形
 平面図形
平面図形
平面図形
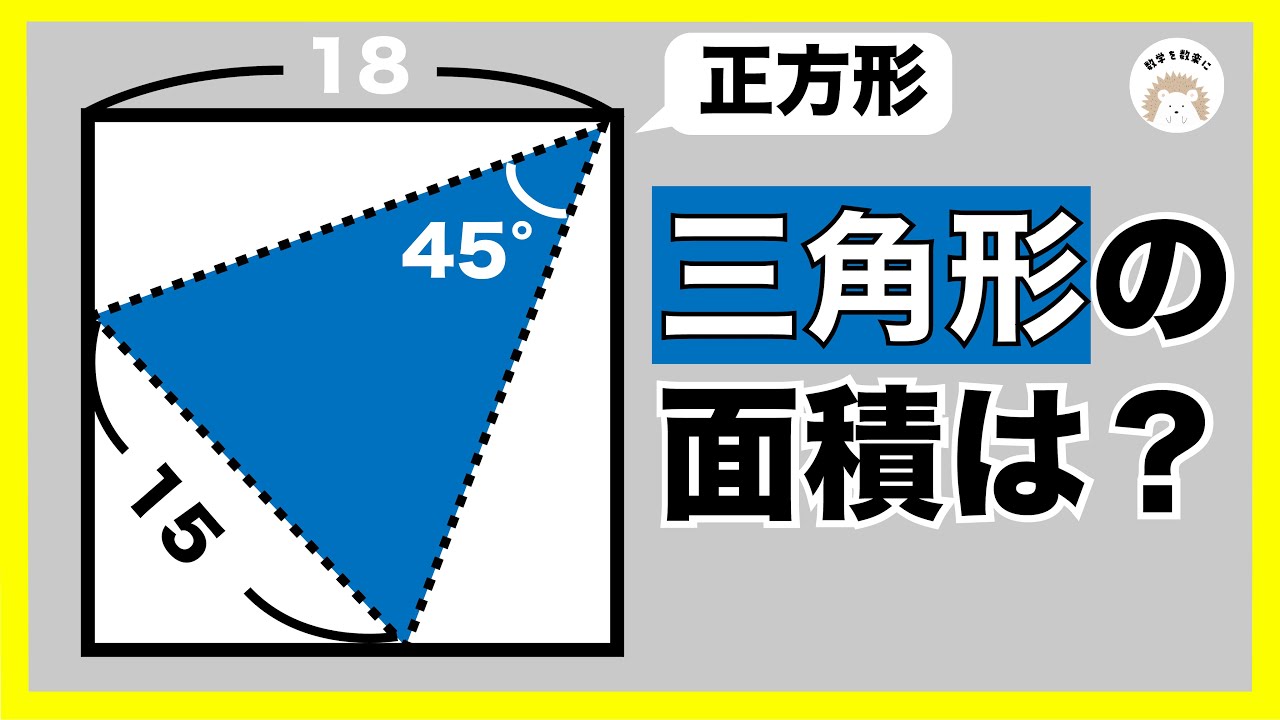
気付けば一瞬!!積の値どう考える?
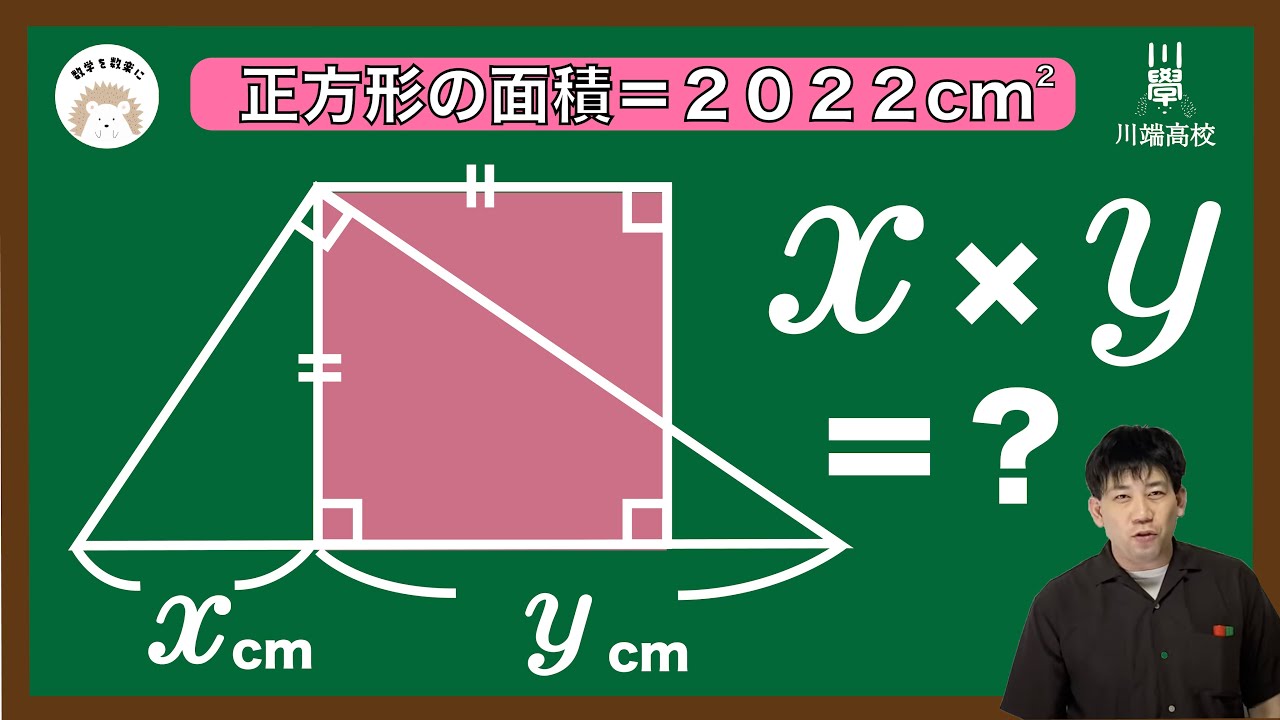
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形の面積=2022㎠
$x \timse y =?$
*図は動画内参照
川端高校
この動画を見る
正方形の面積=2022㎠
$x \timse y =?$
*図は動画内参照
川端高校
気づけば一瞬!!!
角の名前

トイック満点講師森鉄に球の体積の公式を教えるよ

【使える知識は…限られる!】図形:活水高等学校~全国入試問題解法
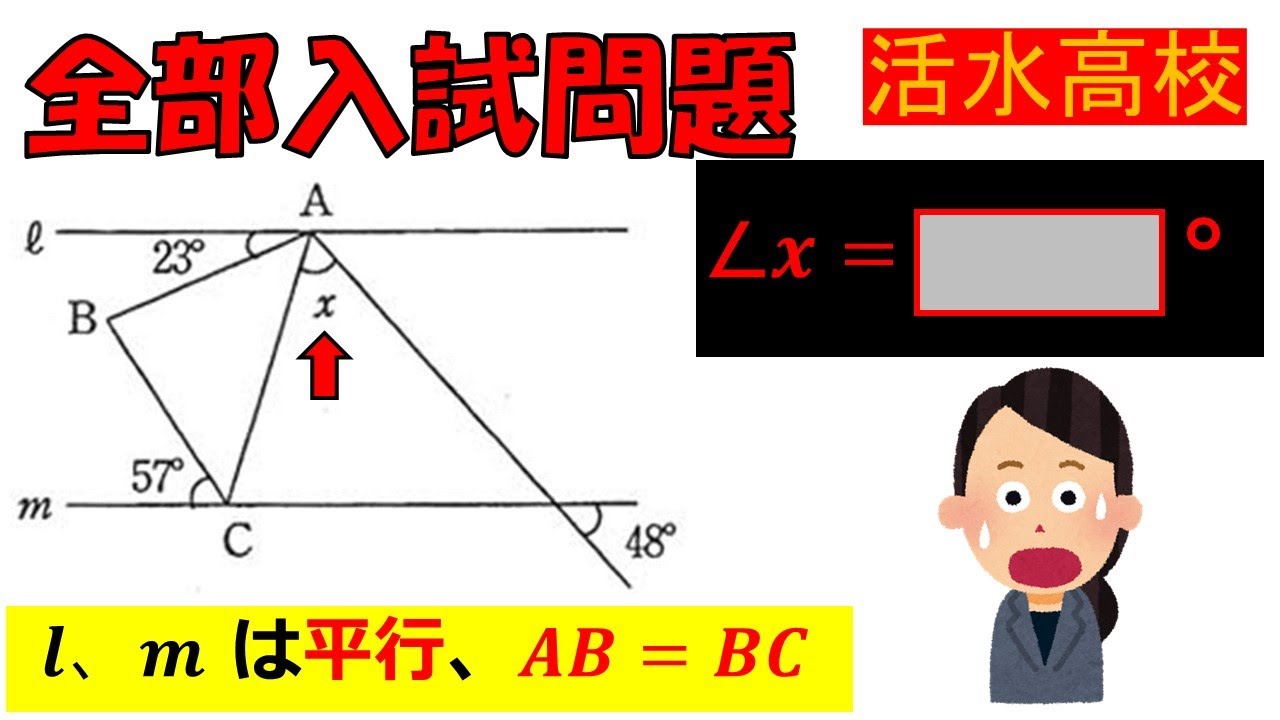
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$l,m$は平行であり,$AB=BC$である.
$\angle x=\Box$である.
活水高等学校過去問
この動画を見る
$l,m$は平行であり,$AB=BC$である.
$\angle x=\Box$である.
活水高等学校過去問
2通りで解説 内角が等しい六角形 筑波附属
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
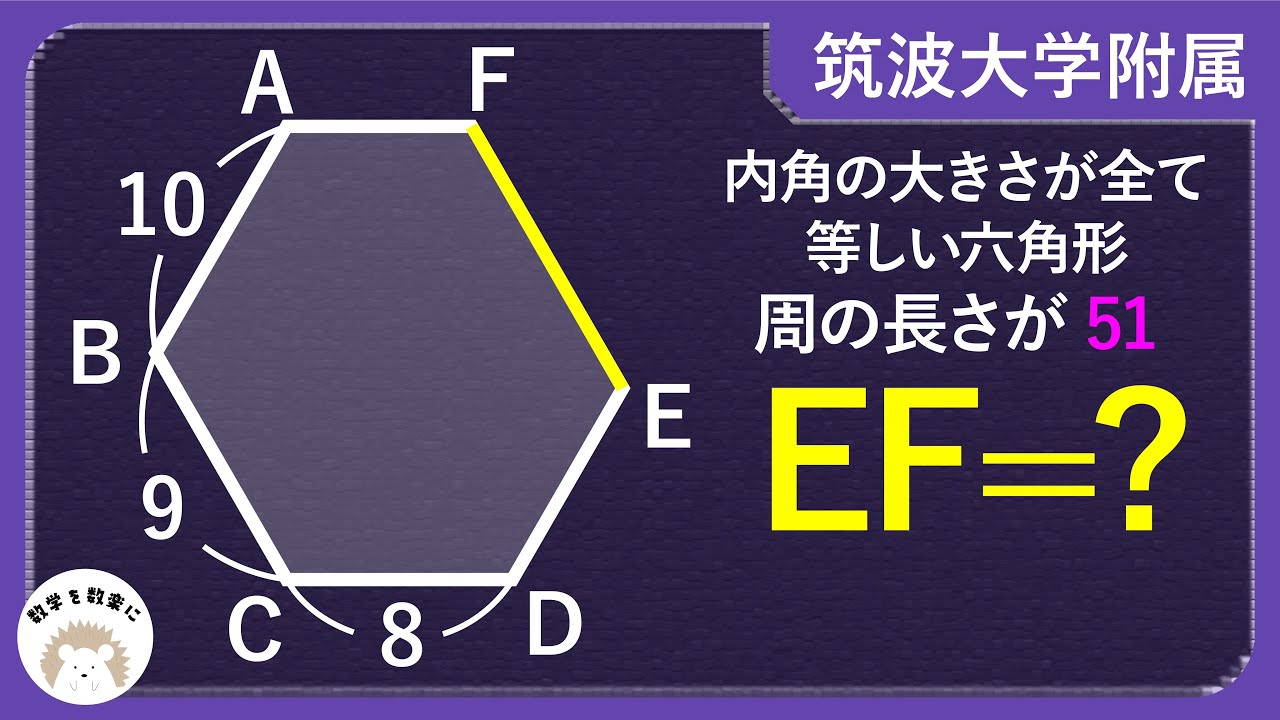
内角の大きさが全て等しい六角形
周の長さが51
EF=?
*図は動画内参照
筑波大学附属高等学校
この動画を見る
内角の大きさが全て等しい六角形
周の長さが51
EF=?
*図は動画内参照
筑波大学附属高等学校
正9角形 弘学館
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
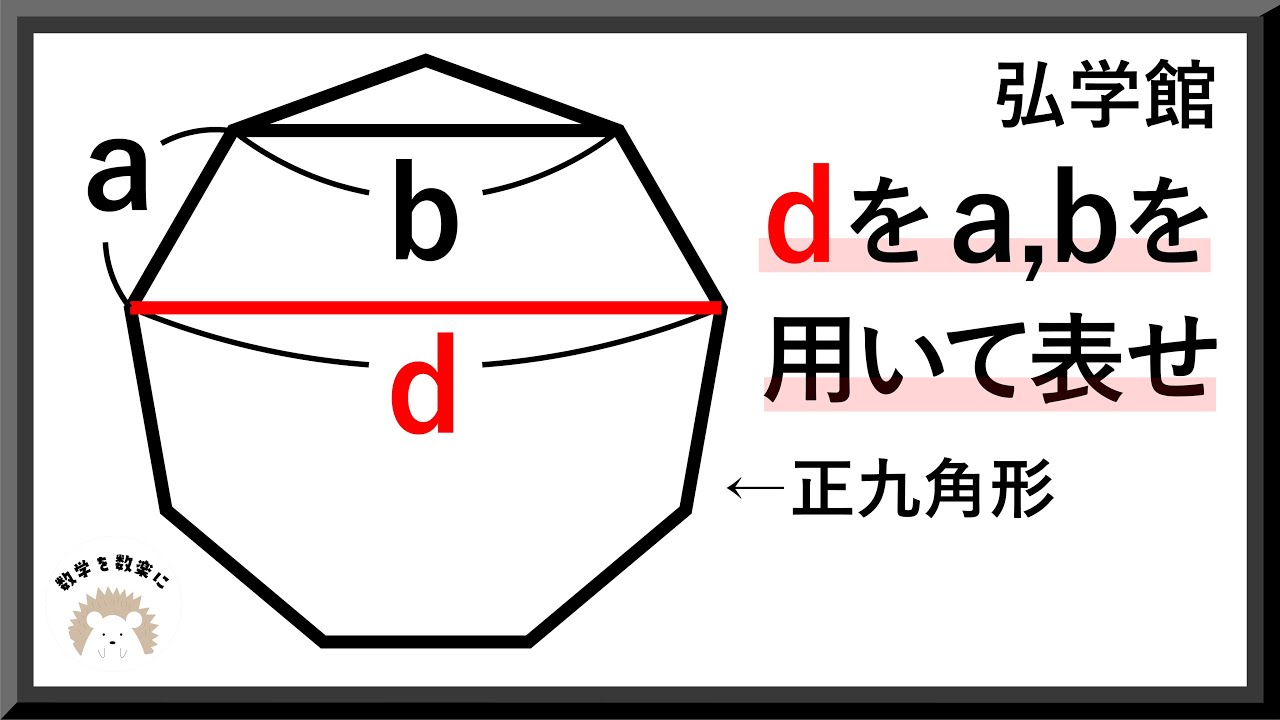
正九角形
dをa,bを用いて表せ
*図は動画内参照
弘学館高等学校
この動画を見る
正九角形
dをa,bを用いて表せ
*図は動画内参照
弘学館高等学校
ロニー先生の問題

【困難は分割せよ!】図形:名古屋女子大学高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
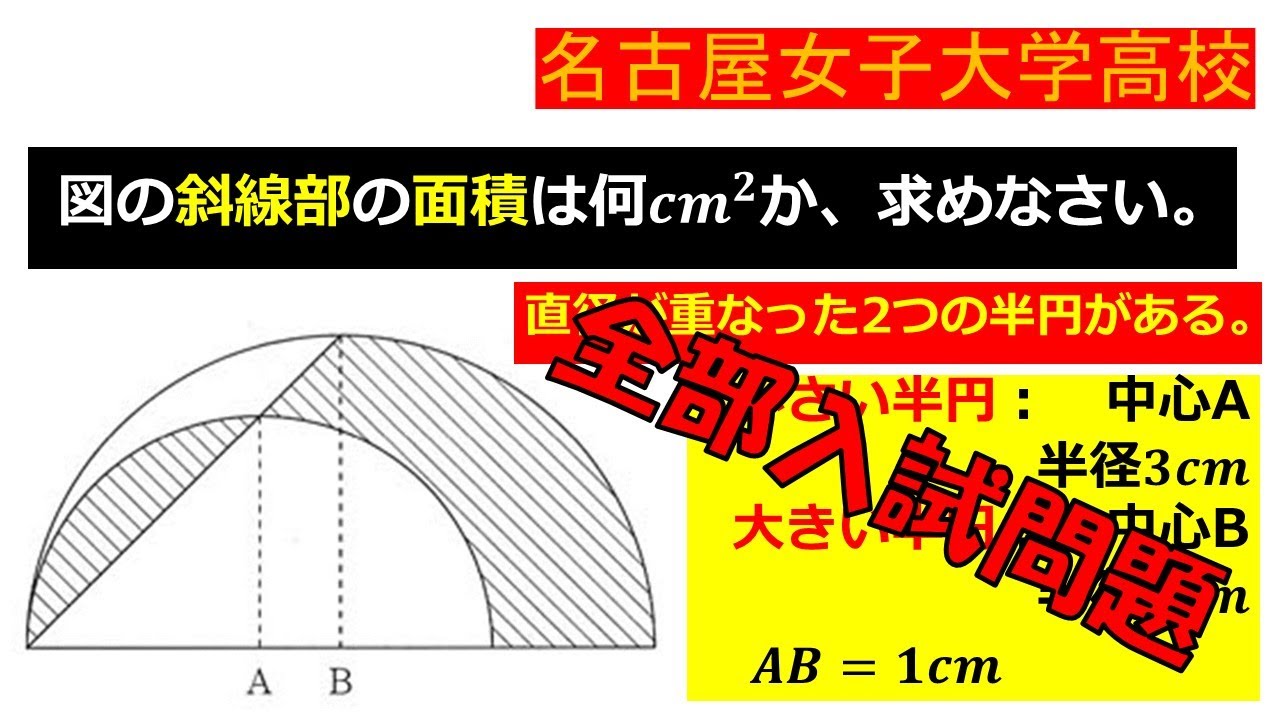
図の斜線部の面積は何$cm^2$か,求めなさい.
名古屋女子大学高等学校過去問
この動画を見る
図の斜線部の面積は何$cm^2$か,求めなさい.
名古屋女子大学高等学校過去問
【全員集合!】図形:椙山女学園高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
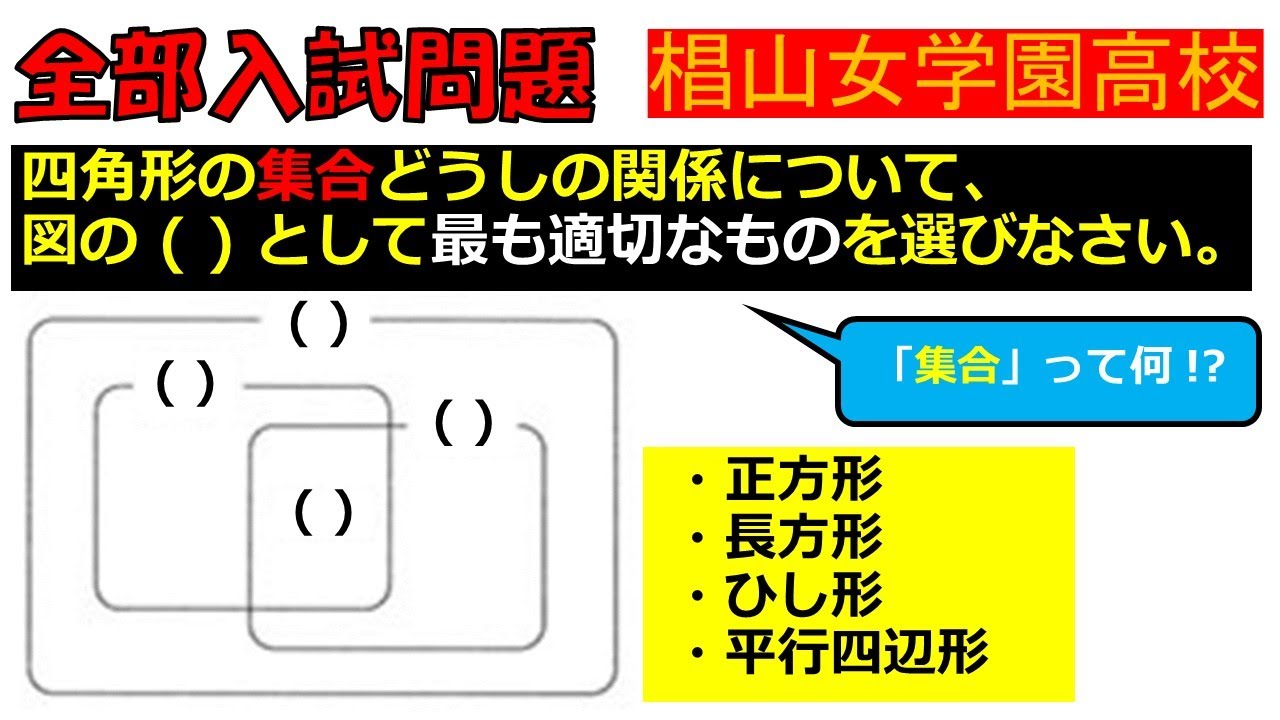
四角形の集合どうしの関係について,図の()として最も適切なものを選びなさい.
椙山女学園高等学校過去問
この動画を見る
四角形の集合どうしの関係について,図の()として最も適切なものを選びなさい.
椙山女学園高等学校過去問
【見慣れない図形にどう対処するか】図形:椙山女学園高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
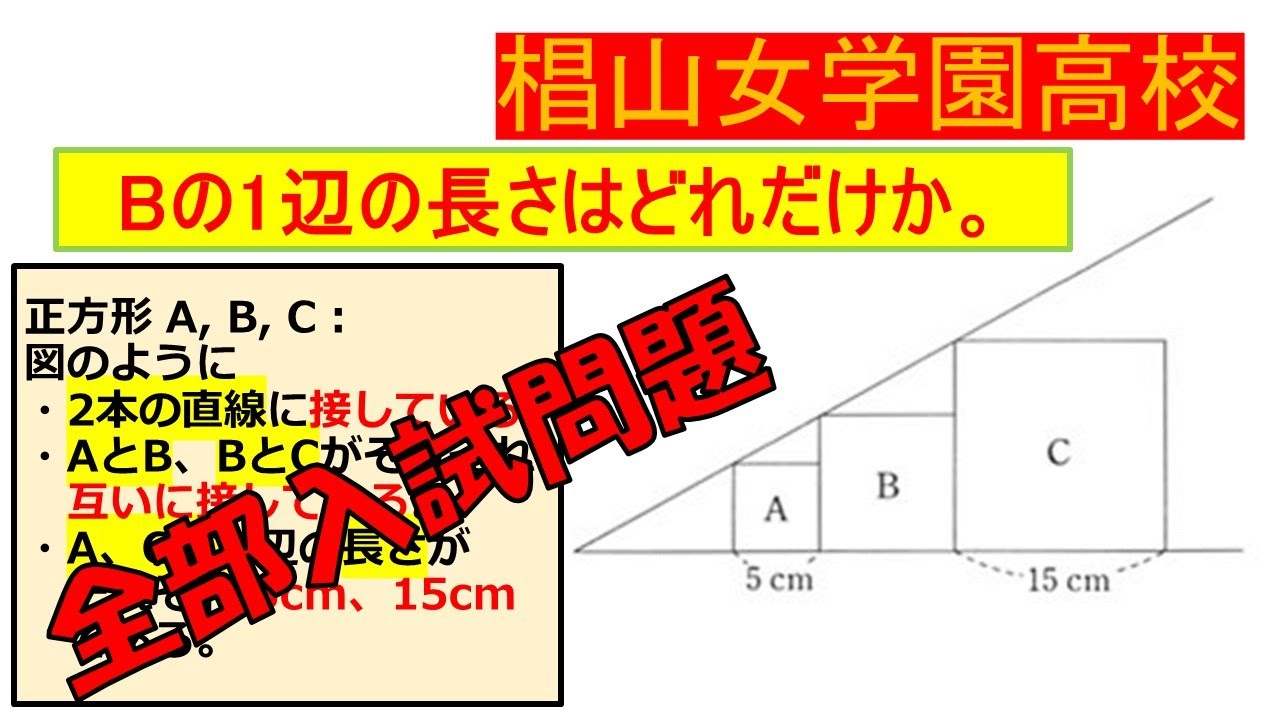
正方形$A,B,C$は図のように2本の直線に接している.
$A$と$B$,$B$と$C$がそれぞれ互いに接している.
$A,C$の1辺の長さがそれぞれ$5cm,15cm$である.
$B$の1辺の長さはどれだけか.
椙山女学園高等学校過去問
この動画を見る
正方形$A,B,C$は図のように2本の直線に接している.
$A$と$B$,$B$と$C$がそれぞれ互いに接している.
$A,C$の1辺の長さがそれぞれ$5cm,15cm$である.
$B$の1辺の長さはどれだけか.
椙山女学園高等学校過去問
平面図形は公立が面白い 愛知県(改) 令和4年度 2022 入試問題100題解説89問目!
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
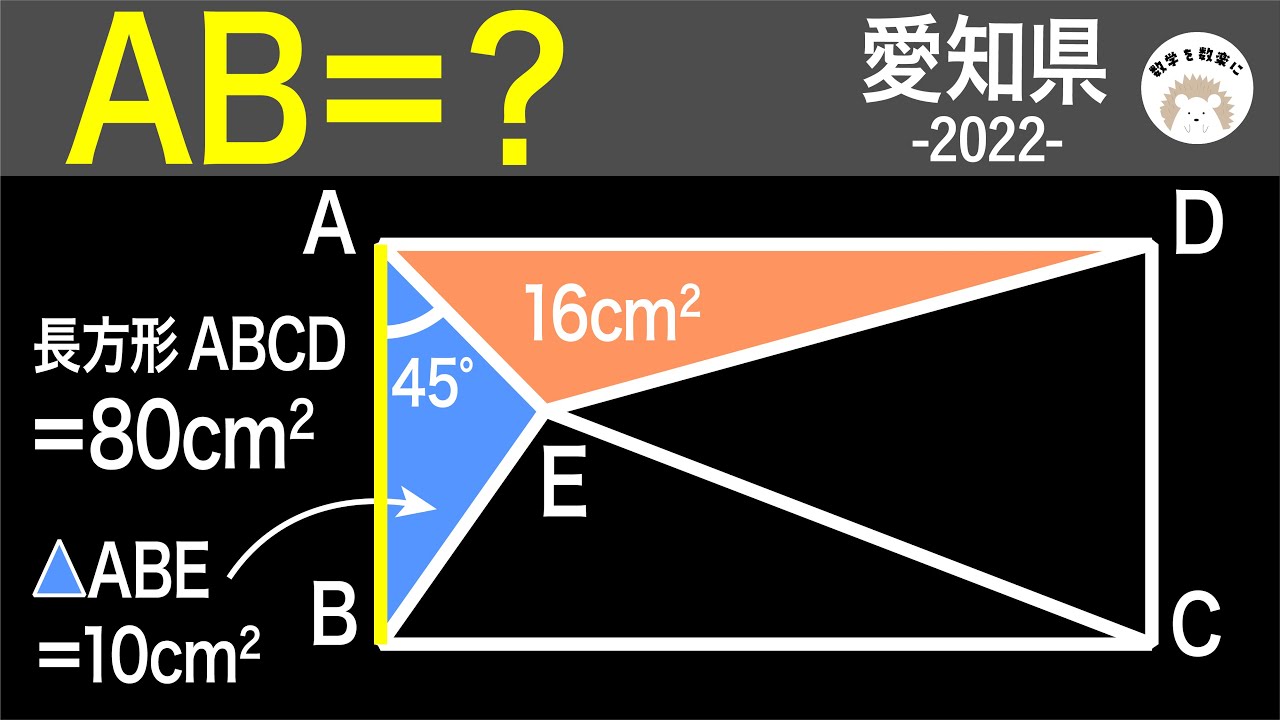
長方形ABCD=80㎠
△ABE=10㎠
AB=?
*図は動画内参照
2022愛知県
この動画を見る
長方形ABCD=80㎠
△ABE=10㎠
AB=?
*図は動画内参照
2022愛知県
動体視力と数学を鍛えるダイエット女子~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において,$BC$の中点を$M$とするとき,
$\overline{AB^2}+\overline{AC^2}=2(\overline{AM^2}+\overline{BM^2})$
上式を座標を用いて証明せよ.
この動画を見る
$\triangle ABC$において,$BC$の中点を$M$とするとき,
$\overline{AB^2}+\overline{AC^2}=2(\overline{AM^2}+\overline{BM^2})$
上式を座標を用いて証明せよ.
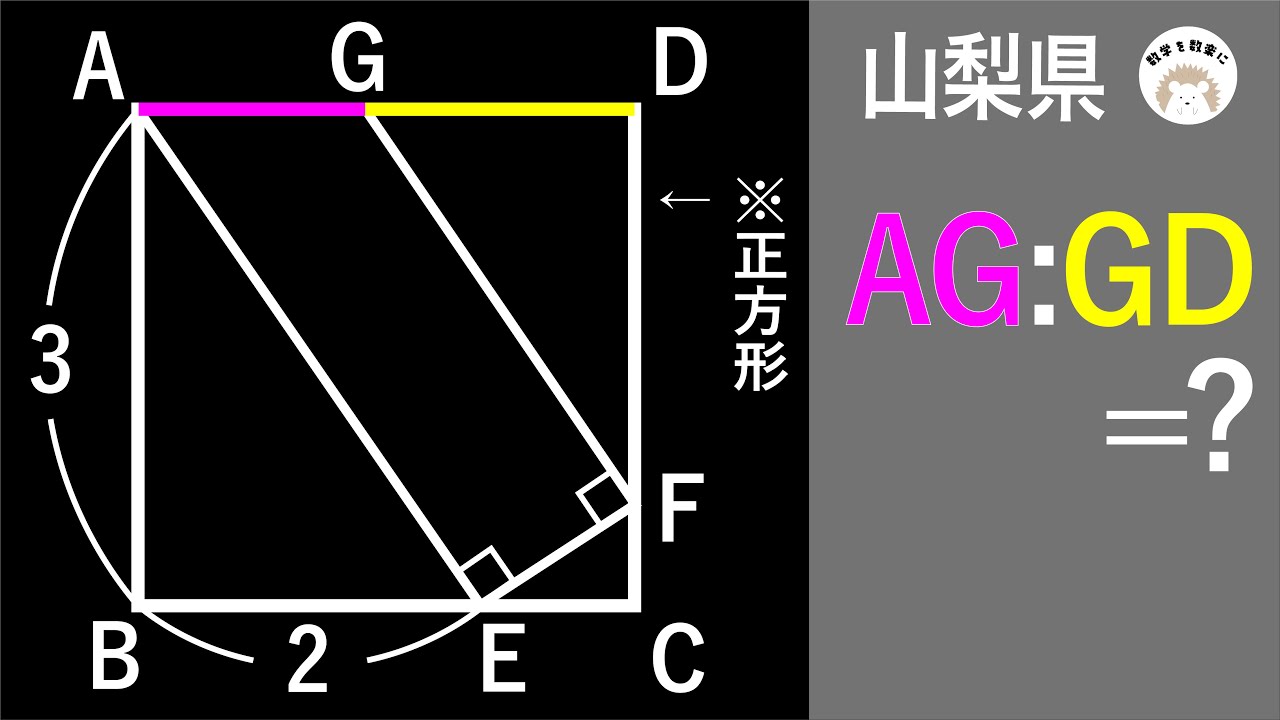
正方形 令和4年度 山梨県 2022 入試問題100題解説82問目!
【困難は分割せよ!】図形:ノートルダム女学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
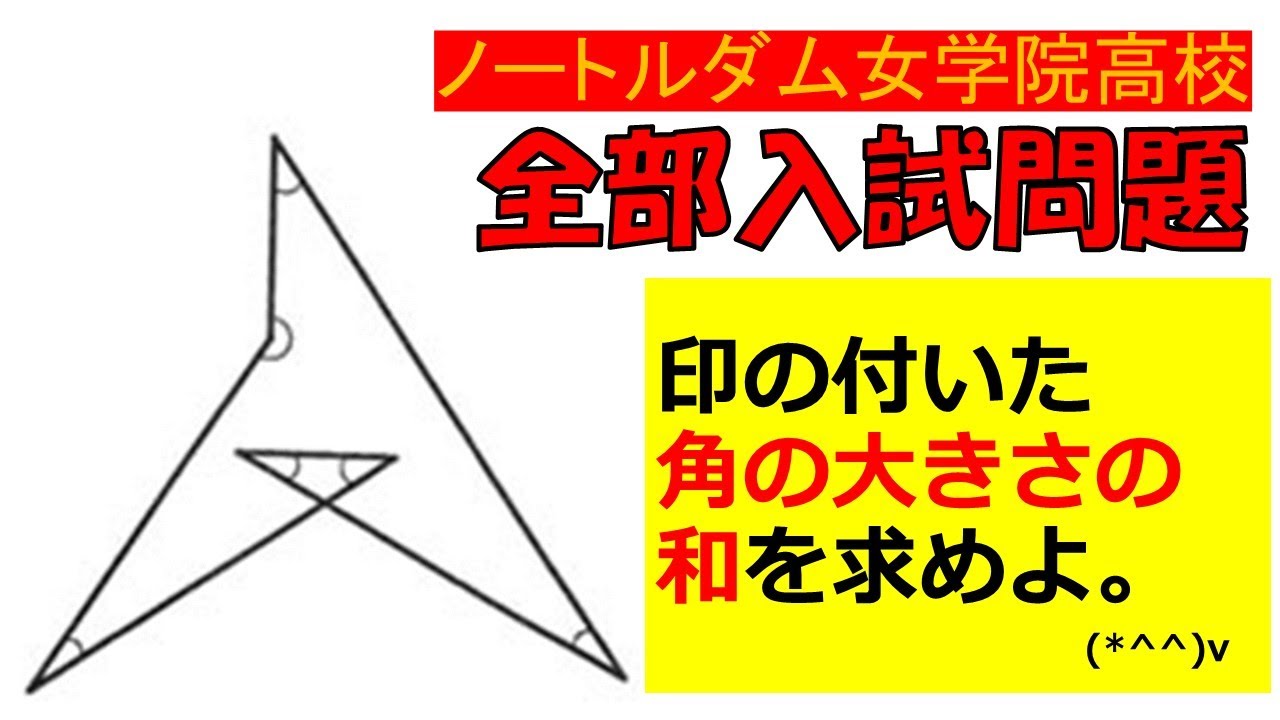
印の付いた角の大きさの和を求めよ.
ノートルダム女学院高校過去問
この動画を見る
印の付いた角の大きさの和を求めよ.
ノートルダム女学院高校過去問
高等学校入試予想問題:富山県~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平行と合同#文字と式#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$6a^2b\times 2b\div 3ab$を計算せよ.
(2)$\sqrt{32}-\sqrt{18}+\sqrt2$を計算せよ.
(3)$x^2-5x-24=0$を解け.
(4)「$am$のリボンから.$bcm$切り取ると残りの長さは$2m$より短い.」
不等式で表せ.
(5)$\angle x$は何度か.
$\boxed{2}$
(1)7番目の図形と16番目の図形の面積をそれぞれ求めよ.
(2)$n$を偶数とするとき,$n$番目の図形と$(2n+1)$番目の図形の面積の差が$331cm^2$である.$n$はいくつか.
$boxed{3}$
$A,B,C,D,E$は円$O$上の5点である.
$AC,BD$は直径であり,$AD\parallel BD$,交点は$F,G$である.
(1)$CE=?,OG=?$
(2)$FG=?$
(3)$\triangle ACF$と$\triangle ODA$の面積比は?
この動画を見る
$\boxed{1}$
(1)$6a^2b\times 2b\div 3ab$を計算せよ.
(2)$\sqrt{32}-\sqrt{18}+\sqrt2$を計算せよ.
(3)$x^2-5x-24=0$を解け.
(4)「$am$のリボンから.$bcm$切り取ると残りの長さは$2m$より短い.」
不等式で表せ.
(5)$\angle x$は何度か.
$\boxed{2}$
(1)7番目の図形と16番目の図形の面積をそれぞれ求めよ.
(2)$n$を偶数とするとき,$n$番目の図形と$(2n+1)$番目の図形の面積の差が$331cm^2$である.$n$はいくつか.
$boxed{3}$
$A,B,C,D,E$は円$O$上の5点である.
$AC,BD$は直径であり,$AD\parallel BD$,交点は$F,G$である.
(1)$CE=?,OG=?$
(2)$FG=?$
(3)$\triangle ACF$と$\triangle ODA$の面積比は?
高等学校入学試験問題予想:岐阜県~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#平行と合同#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$4+10\div(-2)$を計算せよ.
(2)$2(4x-y)-(7x-5y)$を計算せよ.
(3)$6ab\div 2a\times b$を計算せよ.
(4)次の数を大きい順に左から並べなさい.
$2\sqrt2,\sqrt7,3$
$\boxed{2}$
(1)$\angle GHF=?$
(2)$\triangle GHF \backsim \triangle FDE$の証明
(3)$AG=3cm,GF=5cm$のとき,$HF=?,AB=?,\triangle FDE=?$
岐阜県立高校過去問
この動画を見る
$\boxed{1}$
(1)$4+10\div(-2)$を計算せよ.
(2)$2(4x-y)-(7x-5y)$を計算せよ.
(3)$6ab\div 2a\times b$を計算せよ.
(4)次の数を大きい順に左から並べなさい.
$2\sqrt2,\sqrt7,3$
$\boxed{2}$
(1)$\angle GHF=?$
(2)$\triangle GHF \backsim \triangle FDE$の証明
(3)$AG=3cm,GF=5cm$のとき,$HF=?,AB=?,\triangle FDE=?$
岐阜県立高校過去問
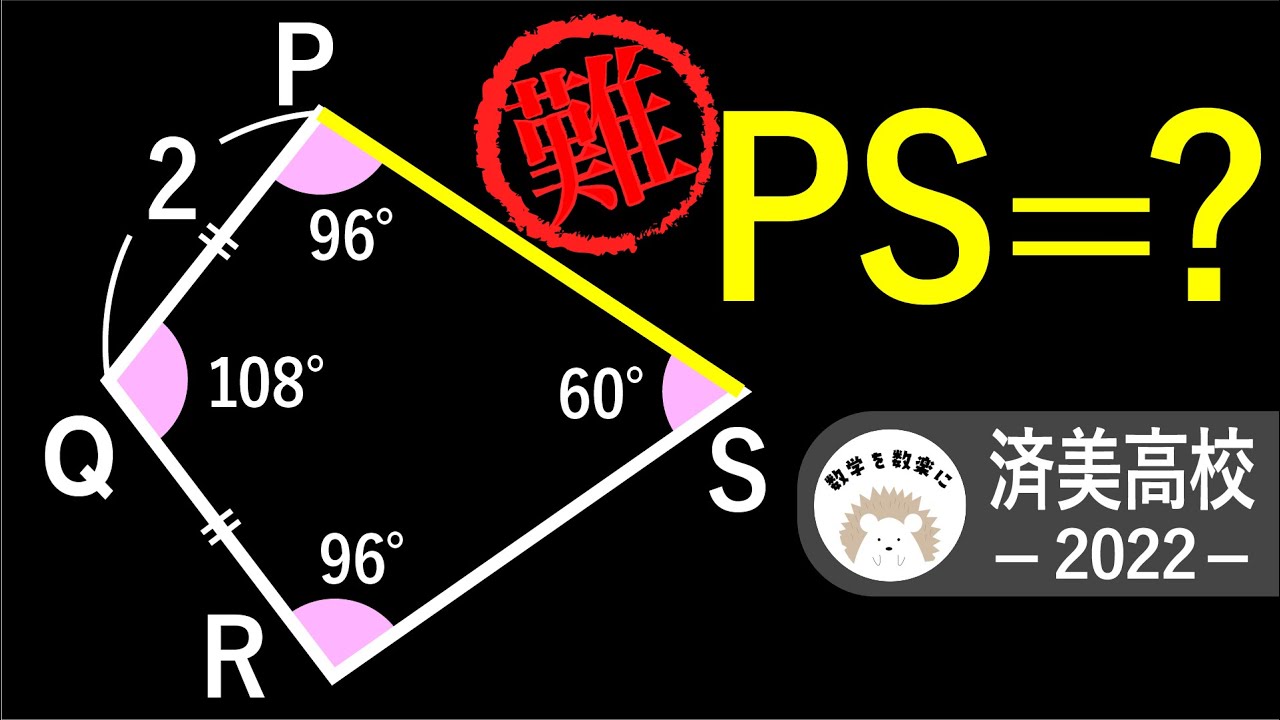
誘導なしだと難しい 済美高校2022入試問題解説33問目
単元:
#数学(中学生)#中1数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
PS=?
*図は動画内参照
2022済美高等学校
この動画を見る
PS=?
*図は動画内参照
2022済美高等学校
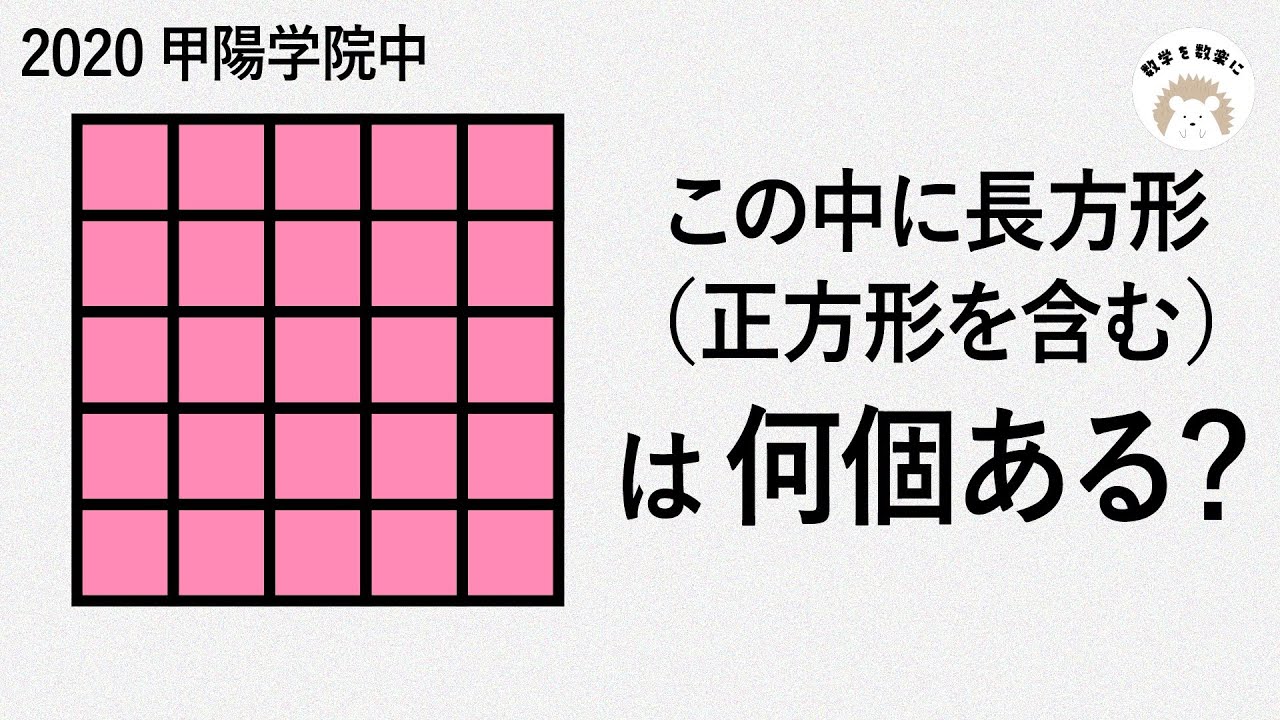
長方形何個? 甲陽学院中
単元:
#算数(中学受験)#中1数学#過去問解説(学校別)#平面図形#角度と面積#平面図形
指導講師:
数学を数楽に
問題文全文(内容文):
この中に長方形(正方形を含む)は何個ある?
*図は動画内参照
2020甲陽学院中学校
この動画を見る
この中に長方形(正方形を含む)は何個ある?
*図は動画内参照
2020甲陽学院中学校
なんで円の面積は半径×半径×π?

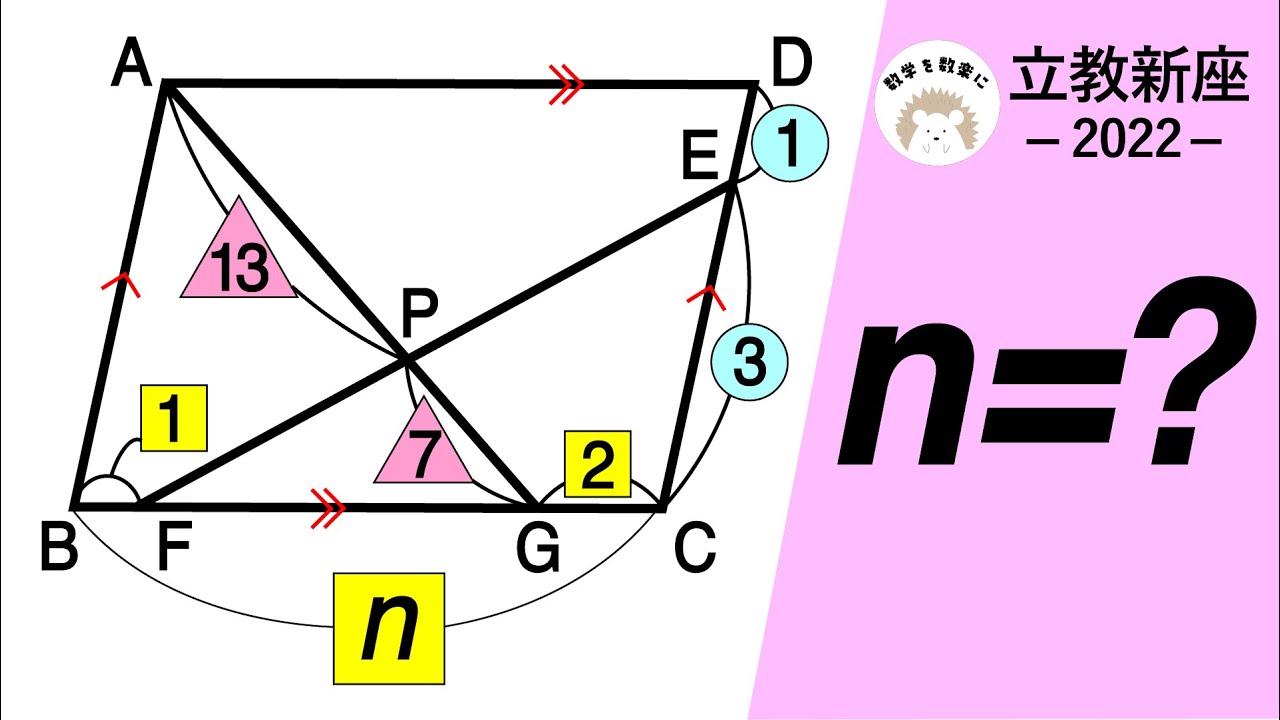
図形 比 立教新座 2022 入試問題解説 29問目
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
n=?
*図は動画内参照
2022立教新座高等学校(改)
この動画を見る
n=?
*図は動画内参照
2022立教新座高等学校(改)
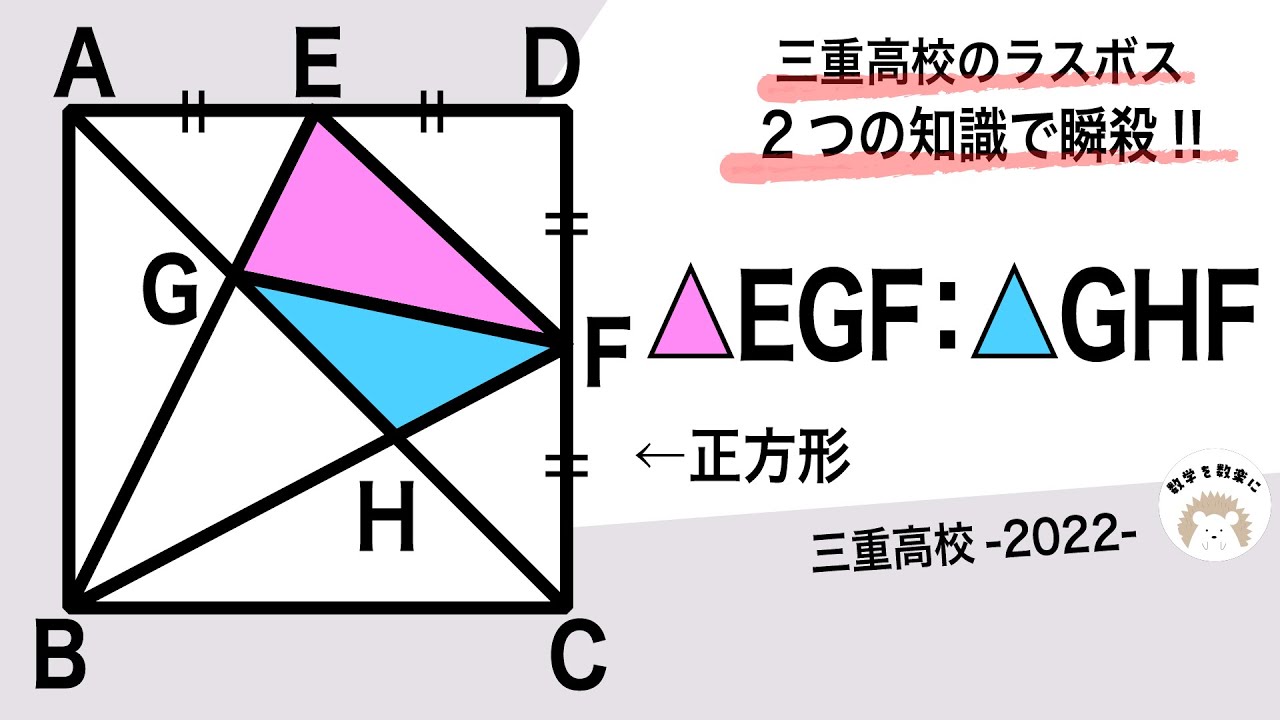
面積比 三重高校のラスト問題2022入試問題解説 24問目
単元:
#数学(中学生)#中1数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△EGF:△GHF
*図は動画内参照
2022三重高等学校
この動画を見る
△EGF:△GHF
*図は動画内参照
2022三重高等学校
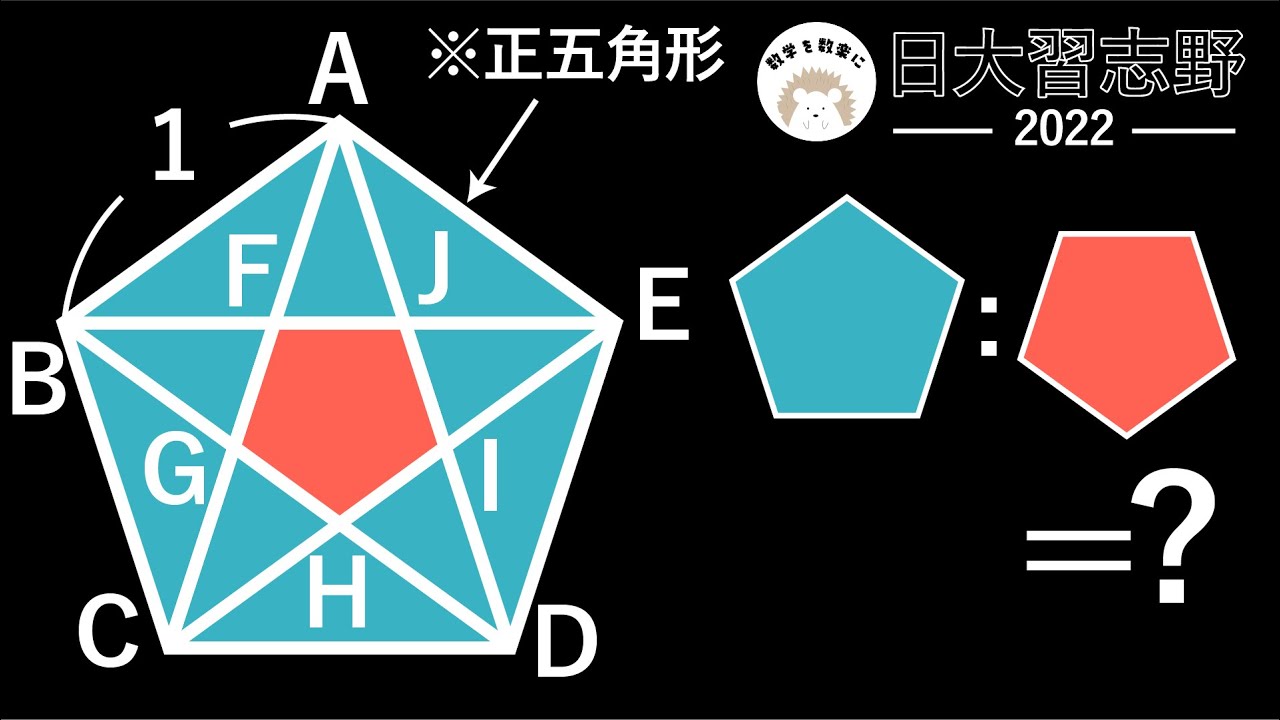
正五角形の対角線の長さと面積比 日大習志野2022 入試問題解説 9問目
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)AC=?
(2)五角形ABCDE:五角形FGHIJ
*図は動画内参照
2022日本大学習志野高等学校
この動画を見る
(1)AC=?
(2)五角形ABCDE:五角形FGHIJ
*図は動画内参照
2022日本大学習志野高等学校
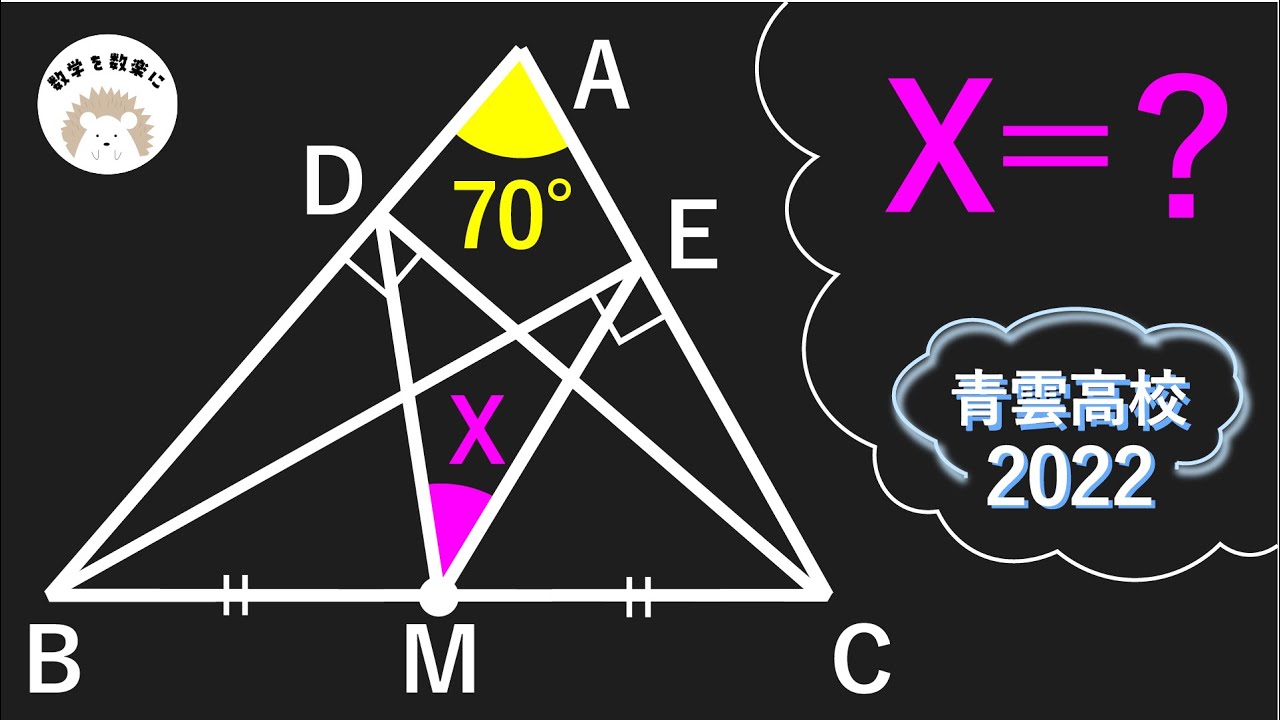
見える? 青雲 2022入試問題解説6問目
単元:
#数学(中学生)#中1数学#中2数学#平面図形#角度と面積#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle DME =?$
*図は動画内参照
2022青雲高等学校
この動画を見る
$\angle DME =?$
*図は動画内参照
2022青雲高等学校
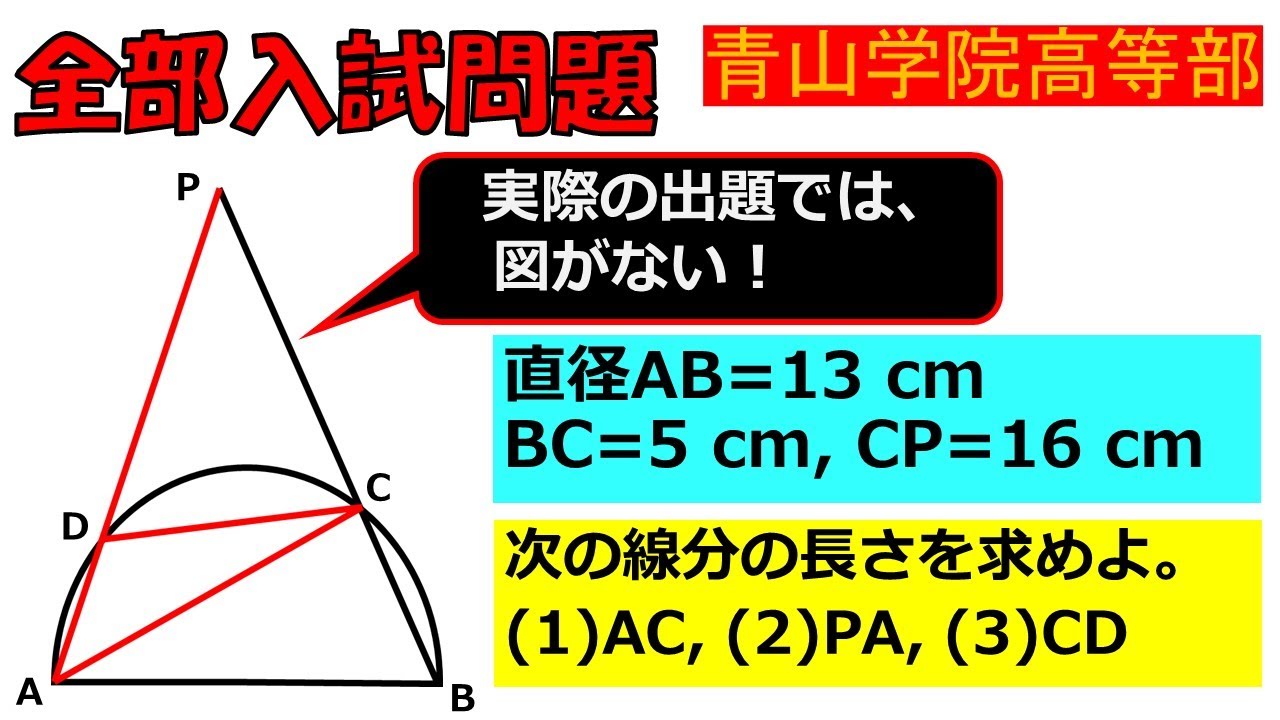
【文章題から図形をイメージする!!】図形:青山学院高等部~全国入試問題解法
単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#青山学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題~青山学院高等部
直径AB=13 cm
BC=5 cm, CP=16 cm
次の線分の長さを求めよ。
録 (1)AC, (2)PA, (3)CD
※図は動画内参照
この動画を見る
入試問題~青山学院高等部
直径AB=13 cm
BC=5 cm, CP=16 cm
次の線分の長さを求めよ。
録 (1)AC, (2)PA, (3)CD
※図は動画内参照
【高校受験対策/数学】死守-97

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
この動画を見る
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
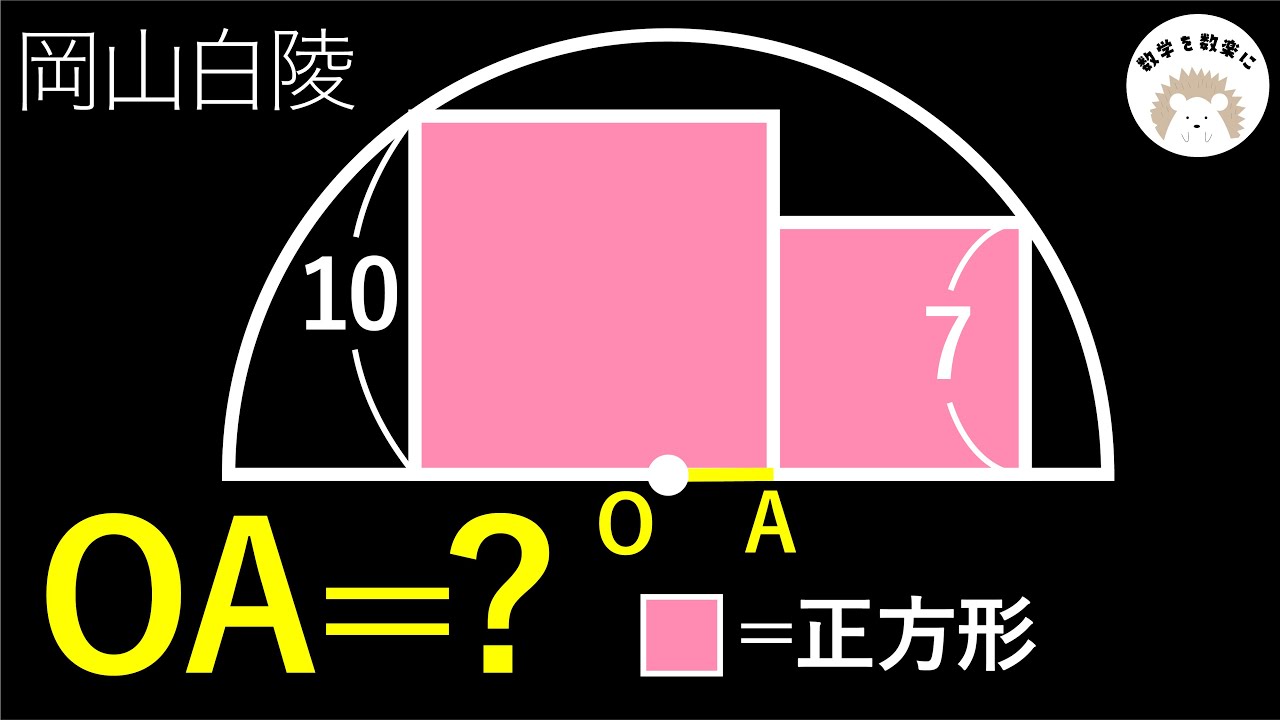
半円と正方形2つ 岡山白陵
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの正方形と半円
OA=?
*図は動画内参照
岡山白陵高等学校
この動画を見る
2つの正方形と半円
OA=?
*図は動画内参照
岡山白陵高等学校
換気せんの面積 名古屋高校
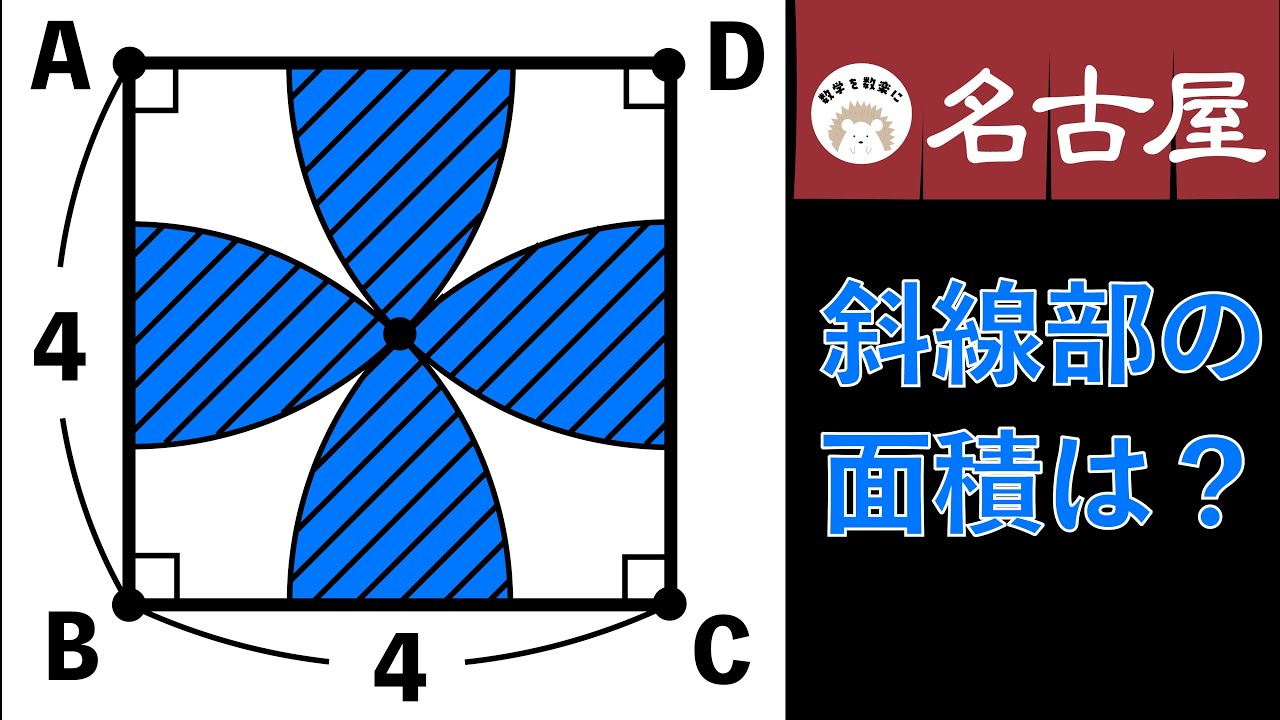
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=?
*図は動画内参照
名古屋高等学校
この動画を見る
斜線部の面積=?
*図は動画内参照
名古屋高等学校
【高校受験対策/数学】死守-96

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#比例・反比例#確率#2次関数#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守96
①$7+2×(-6)$を計算せよ。
②$3(2a+b)-2(4a-5b)$を計算せよ。
③$\frac{14}{\sqrt2}-\sqrt32$を計算せよ。
④2次方程式$(x+6)(x-5)=9x-10$を解け。
⑤関数$y=\frac{1}{2}x^2$について、$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めよ。
⑥関数$y=\frac{ 6 }{ x }$のグラフをかけ。
⑦$△ABC$において、$\angle A=90°,AB=6cm,BC=10cm$のとき、辺$AC$の長さを求めよ。
⑧4枚の硬質A、B、C、Dを同時に投げるとき、少なくとも1枚は表が出る確率を求めよ。
ただし、表と裏が出ることは同様に確からしいとする。
⑨右図のように、円$0$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、$△ABC$をつくる。
線分$BO$を延長した直線と線分$AC$と交点を$D$とする。
$\angle BAC=48°$のとき$\angle ADB$の大きさを求めよ。
この動画を見る
高校受験対策・死守96
①$7+2×(-6)$を計算せよ。
②$3(2a+b)-2(4a-5b)$を計算せよ。
③$\frac{14}{\sqrt2}-\sqrt32$を計算せよ。
④2次方程式$(x+6)(x-5)=9x-10$を解け。
⑤関数$y=\frac{1}{2}x^2$について、$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めよ。
⑥関数$y=\frac{ 6 }{ x }$のグラフをかけ。
⑦$△ABC$において、$\angle A=90°,AB=6cm,BC=10cm$のとき、辺$AC$の長さを求めよ。
⑧4枚の硬質A、B、C、Dを同時に投げるとき、少なくとも1枚は表が出る確率を求めよ。
ただし、表と裏が出ることは同様に確からしいとする。
⑨右図のように、円$0$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、$△ABC$をつくる。
線分$BO$を延長した直線と線分$AC$と交点を$D$とする。
$\angle BAC=48°$のとき$\angle ADB$の大きさを求めよ。
