 三角形と四角形
三角形と四角形
 三角形と四角形
三角形と四角形
2021 京都府 面積比 B 解き方色々
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
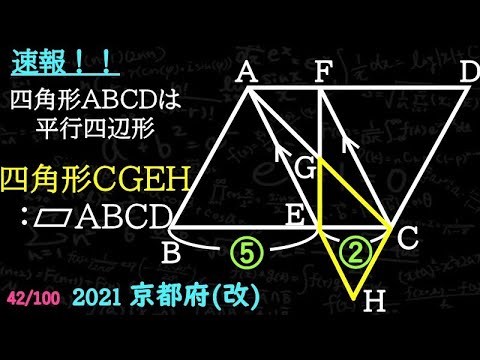
四角形CGEH:平行四辺形ABCD=?
*図は動画内参照
2021京都府
この動画を見る
四角形CGEH:平行四辺形ABCD=?
*図は動画内参照
2021京都府
気付くか、気付かないか。2021明大明治C
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
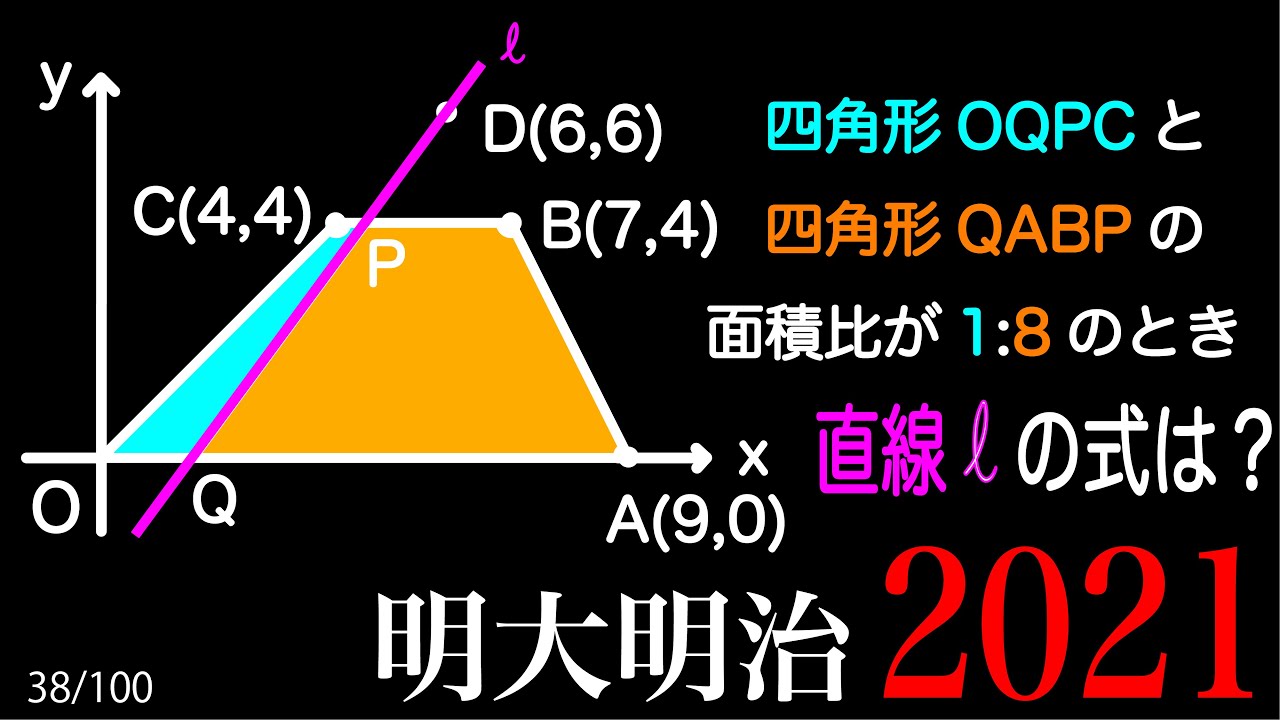
直線lの式は?
*図は動画内参照
2021明治大学付属明治高等学校
この動画を見る
直線lの式は?
*図は動画内参照
2021明治大学付属明治高等学校
【高校受験対策/数学】図形39

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形39
Q.
右の図で、$\triangle ABC$は$\angle BAC=90°$の直角二等辺三角形であり、 $\triangle ADE$は$\angle DAE=90°$の直角二等辺三角形である。
また、点$D$は辺$CB$の延長線上にある。
①$\triangle ADB \equiv \triangle AEC$であることを証明しなさい。
➁$AB=AC=\sqrt{2}cm$、$AD=AE=3cm$のとき、 $DE$の長さを求めなさい。
③➁のとき、$BD$の長さを求めなさい。
この動画を見る
高校受験対策・図形39
Q.
右の図で、$\triangle ABC$は$\angle BAC=90°$の直角二等辺三角形であり、 $\triangle ADE$は$\angle DAE=90°$の直角二等辺三角形である。
また、点$D$は辺$CB$の延長線上にある。
①$\triangle ADB \equiv \triangle AEC$であることを証明しなさい。
➁$AB=AC=\sqrt{2}cm$、$AD=AE=3cm$のとき、 $DE$の長さを求めなさい。
③➁のとき、$BD$の長さを求めなさい。
2021 灘高校 図形 C

単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC△ADEは正三角形
BD>CD
△ADE=$\frac{5}{6}$△ABC
△FDCの面積は△AFEの何倍?
*図は動画内参照
2021灘高等学校
この動画を見る
△ABC△ADEは正三角形
BD>CD
△ADE=$\frac{5}{6}$△ABC
△FDCの面積は△AFEの何倍?
*図は動画内参照
2021灘高等学校
2021 桐朋 角度 B
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
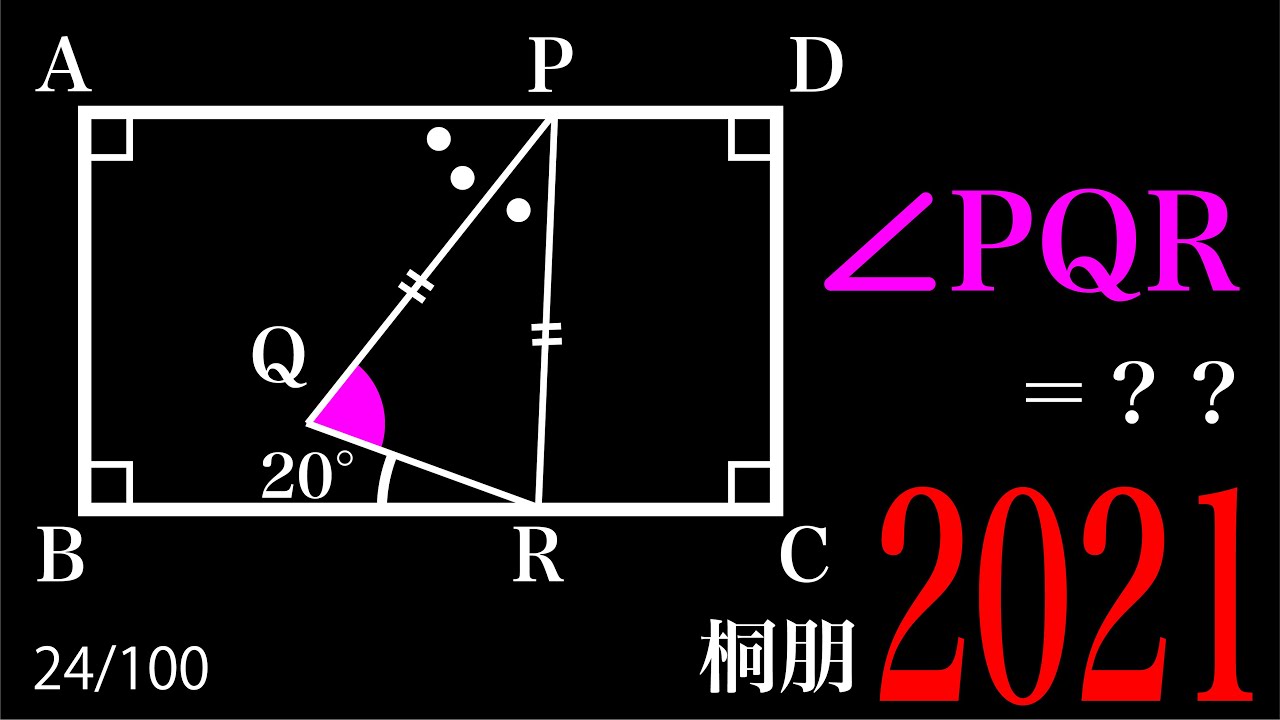
$\angle PQR=?$
*図は動画内参照
2021桐朋高等学校
この動画を見る
$\angle PQR=?$
*図は動画内参照
2021桐朋高等学校
【中学数学】平行四辺形の証明問題が誰でもできるようになる方法~平行四辺形と辺を共有しない問題~【中2数学】

【中学数学】作図の演習~奈良県公立高校入試2019【高校受験】

単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)#奈良県公立高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内図の四角形ABCDは、並行四辺形である。
辺AD上に、ED=$\displaystyle \frac{1}{2}$DCとなる点Eを定規とコンパスを使って作図せよ。
なお、作図に使った線は消さずに残しておくこと。
この動画を見る
動画内図の四角形ABCDは、並行四辺形である。
辺AD上に、ED=$\displaystyle \frac{1}{2}$DCとなる点Eを定規とコンパスを使って作図せよ。
なお、作図に使った線は消さずに残しておくこと。
2021 帝塚山 B 図形問題
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
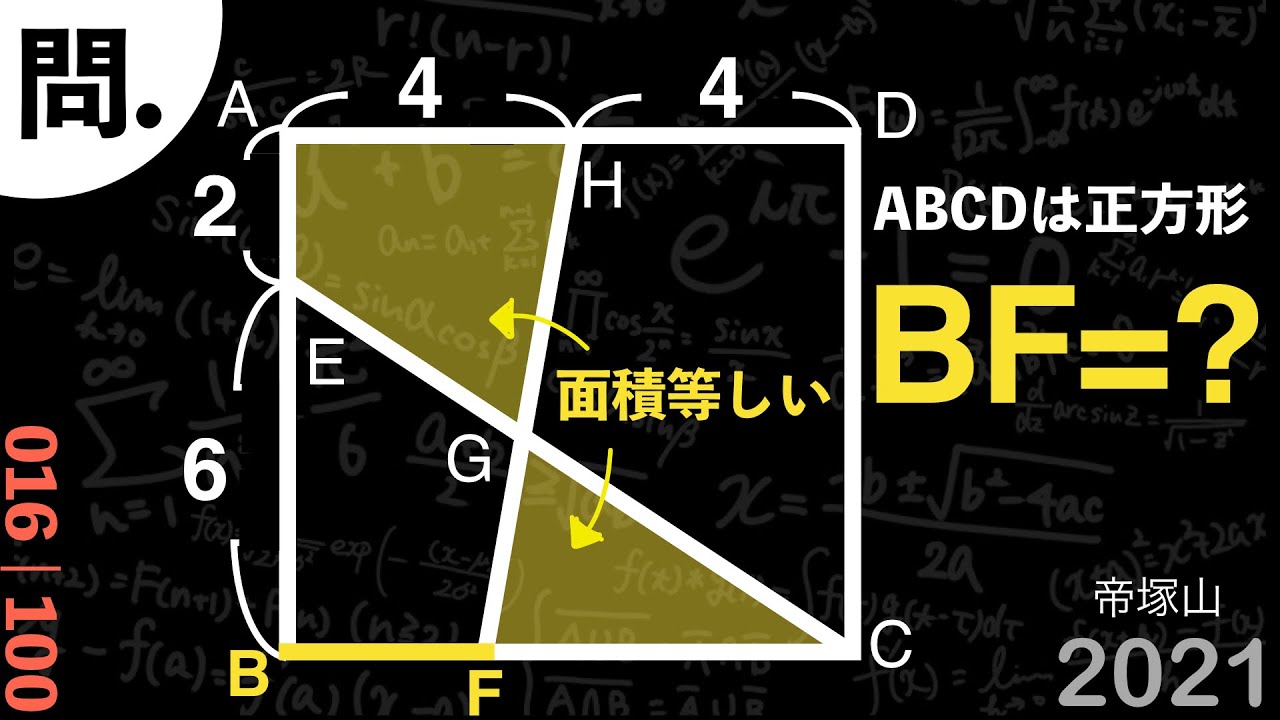
四角形AEGH=△GFC
*図は動画内参照
2021帝塚山高等学校
この動画を見る
四角形AEGH=△GFC
*図は動画内参照
2021帝塚山高等学校
角の和 A 2021帝塚山 読み方間違えてすみませんでした。

【中学数学】平行四辺形の証明問題が誰でもできるようになる方法~平行四辺形と辺を共有する問題~【中2数学】

入試によくでる回転体 A 名古屋2021
単元:
#数学(中学生)#中2数学#立体図形#体積・表面積・回転体・水量・変化のグラフ#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
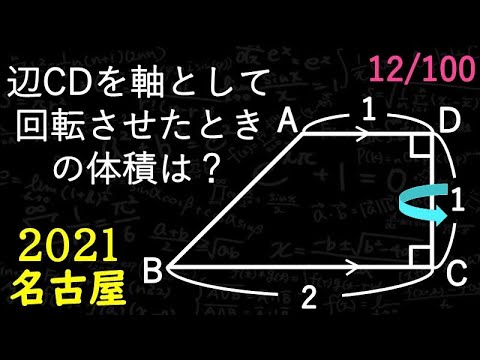
辺CDを軸として回転させたときの立体の体積=?
*図は動画内参照
2021名古屋
この動画を見る
辺CDを軸として回転させたときの立体の体積=?
*図は動画内参照
2021名古屋
道幅の面積 A 2021 名古屋

単元:
#数学(中学生)#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
畑の面積が全体の$\frac{3}{4}$倍となるときの道幅=?
*図は動画内参照
2021名古屋
この動画を見る
畑の面積が全体の$\frac{3}{4}$倍となるときの道幅=?
*図は動画内参照
2021名古屋
ブーメランの角 1対2対3
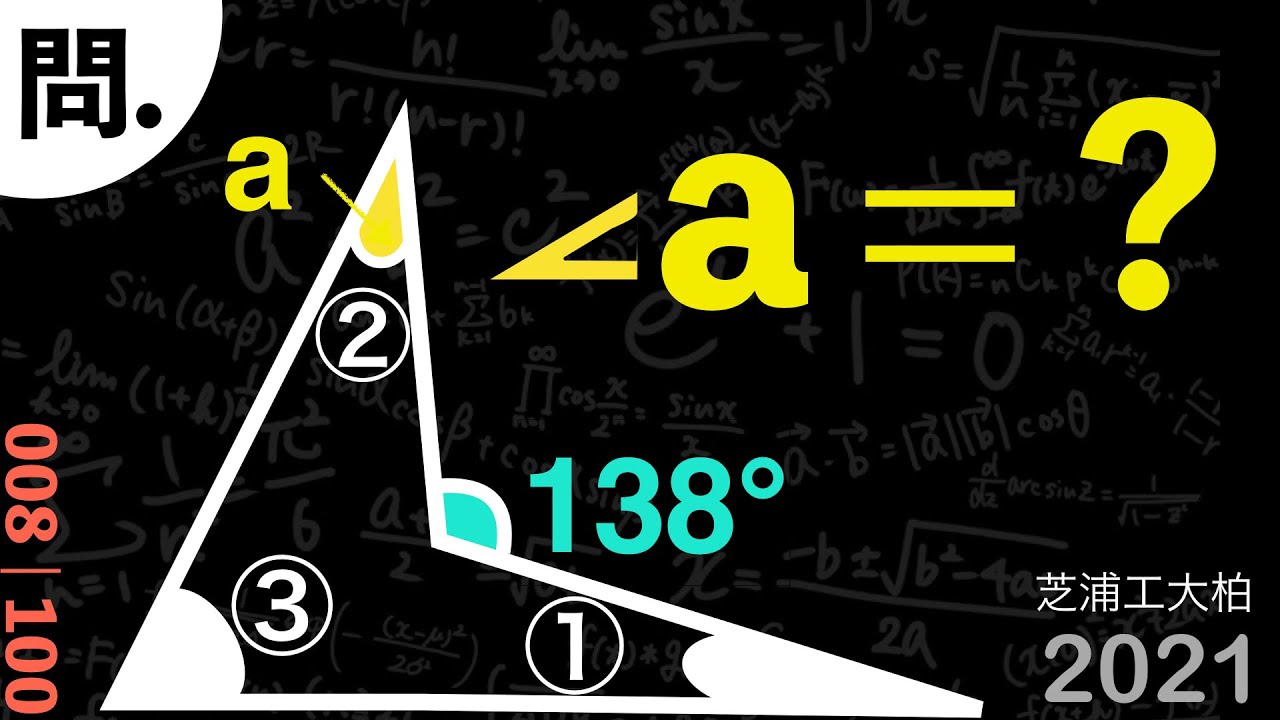
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a =?$
*図は動画内参照
2021芝浦工業大学柏高等学校
この動画を見る
$\angle a =?$
*図は動画内参照
2021芝浦工業大学柏高等学校
相似な図形の面積比 A 専大松戸

単元:
#数学(中学生)#中2数学#中3数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形EBCGの面積=?
*図は動画内参照
2021専修大学松戸高等学校
この動画を見る
四角形EBCGの面積=?
*図は動画内参照
2021専修大学松戸高等学校
長方形の折り返し C 智弁和歌山2021
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
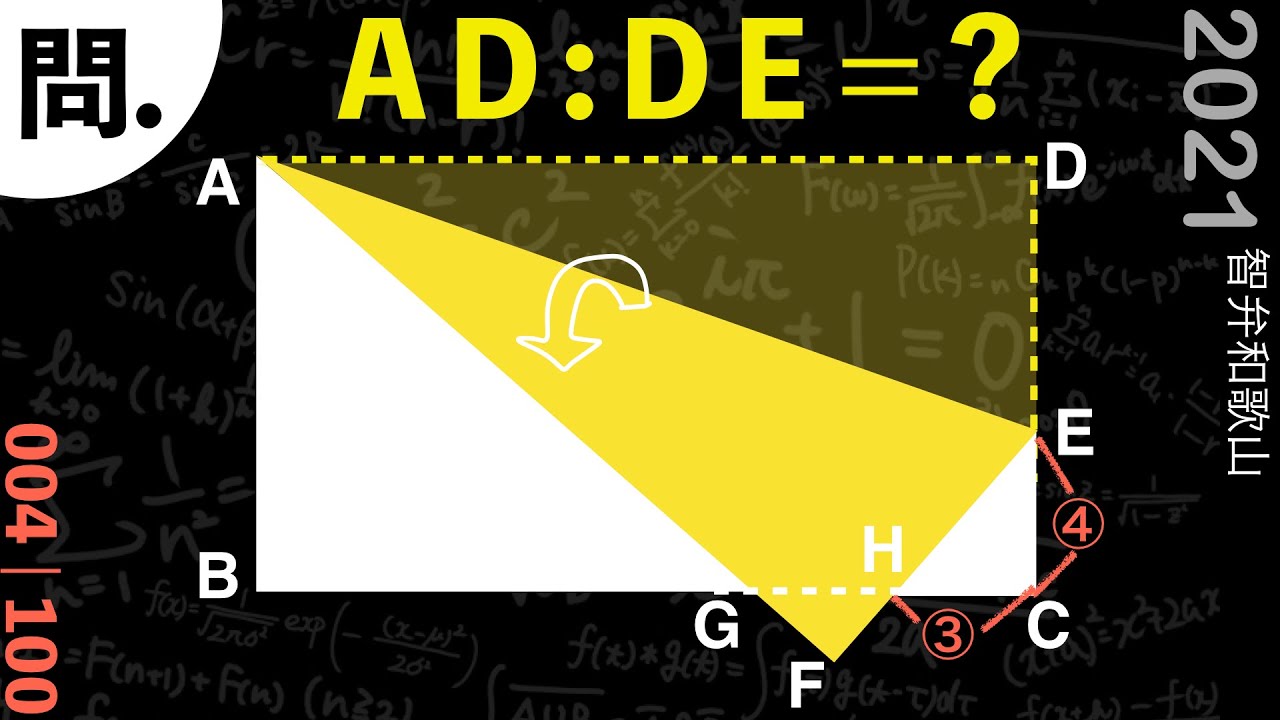
CE:CH = 4:3のとき
AD:DE=?
*図は動画内参照
2021智辯学園和歌山高等学校
この動画を見る
CE:CH = 4:3のとき
AD:DE=?
*図は動画内参照
2021智辯学園和歌山高等学校
直角三角形の中の正方形 A 解き方2通り 岡山白陵
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
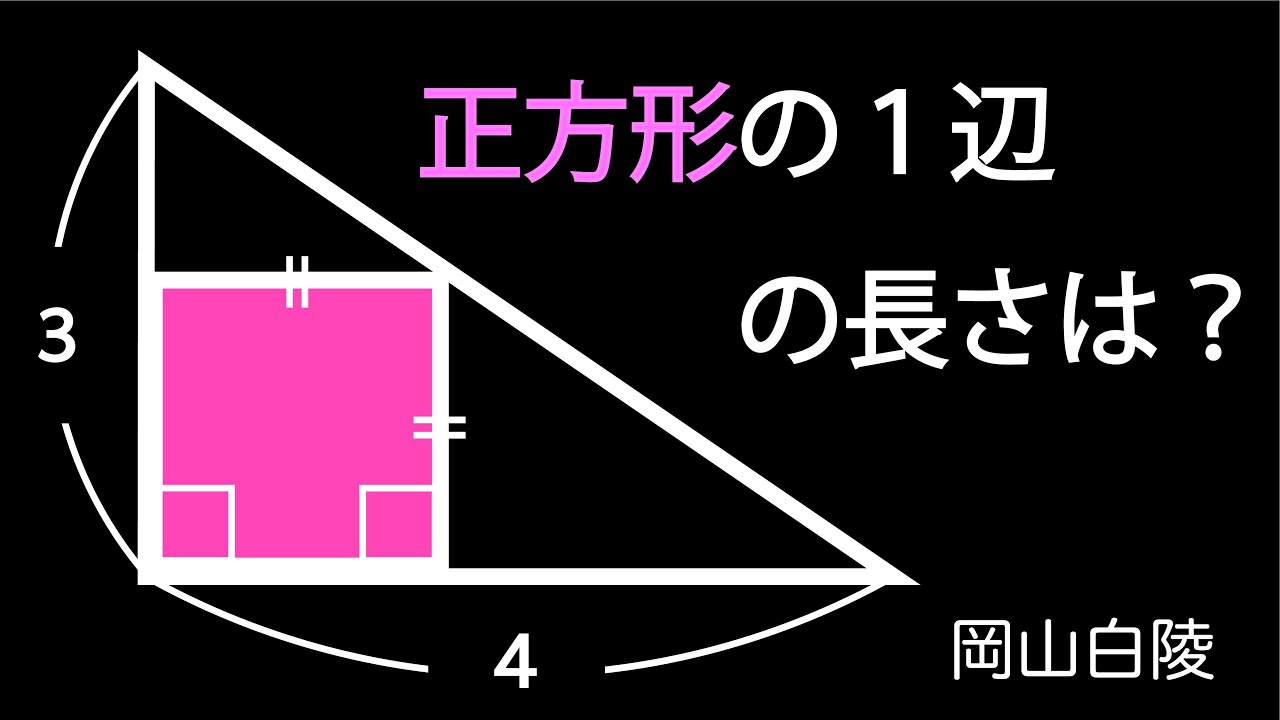
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
この動画を見る
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
【ルーチン】座標上の三角形の面積~全国入試問題解法

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
【ルーチン】座標上の三角形の面積~全国入試問題解法
グラフ上の3点を結んで
三角形の面積を求めよ。
$ S=\displaystyle \frac{1}{2}|x_1y_2-x_2y_1|$
※図は動画内参照
この動画を見る
【ルーチン】座標上の三角形の面積~全国入試問題解法
グラフ上の3点を結んで
三角形の面積を求めよ。
$ S=\displaystyle \frac{1}{2}|x_1y_2-x_2y_1|$
※図は動画内参照
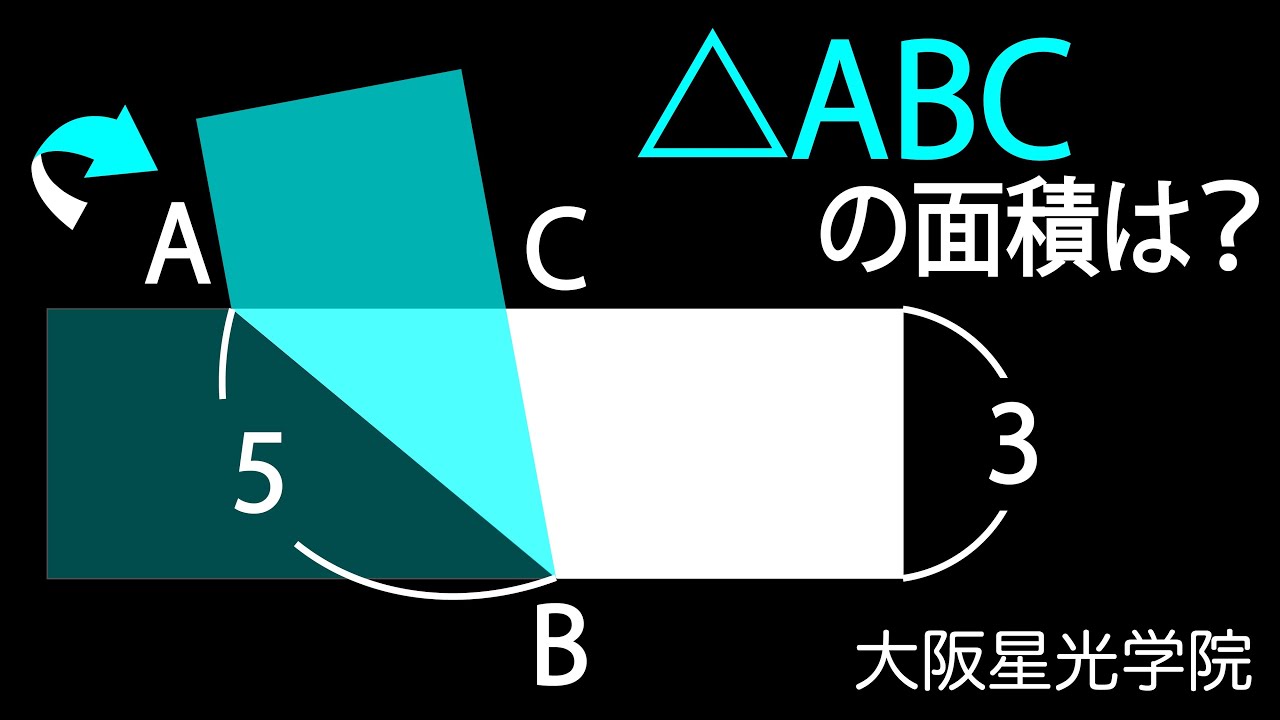
長方形の折り返し 解き方2通り 大阪星光学院
単元:
#数学(中学生)#中2数学#平面図形#図形の移動#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
大阪星光学院高等学校
この動画を見る
△ABC=?
*図は動画内参照
大阪星光学院高等学校
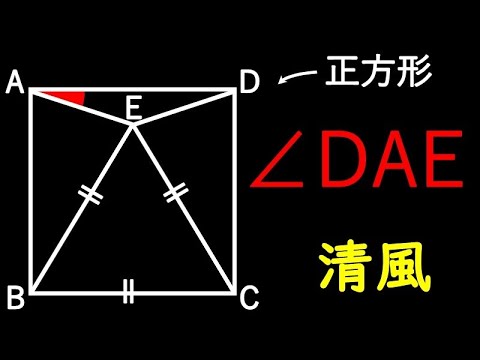
角度を求める A A A (清風)
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABCDは正方形
$\angle DAE=?$
*図は動画内参照
横浜清風高等学校
この動画を見る
四角形ABCDは正方形
$\angle DAE=?$
*図は動画内参照
横浜清風高等学校
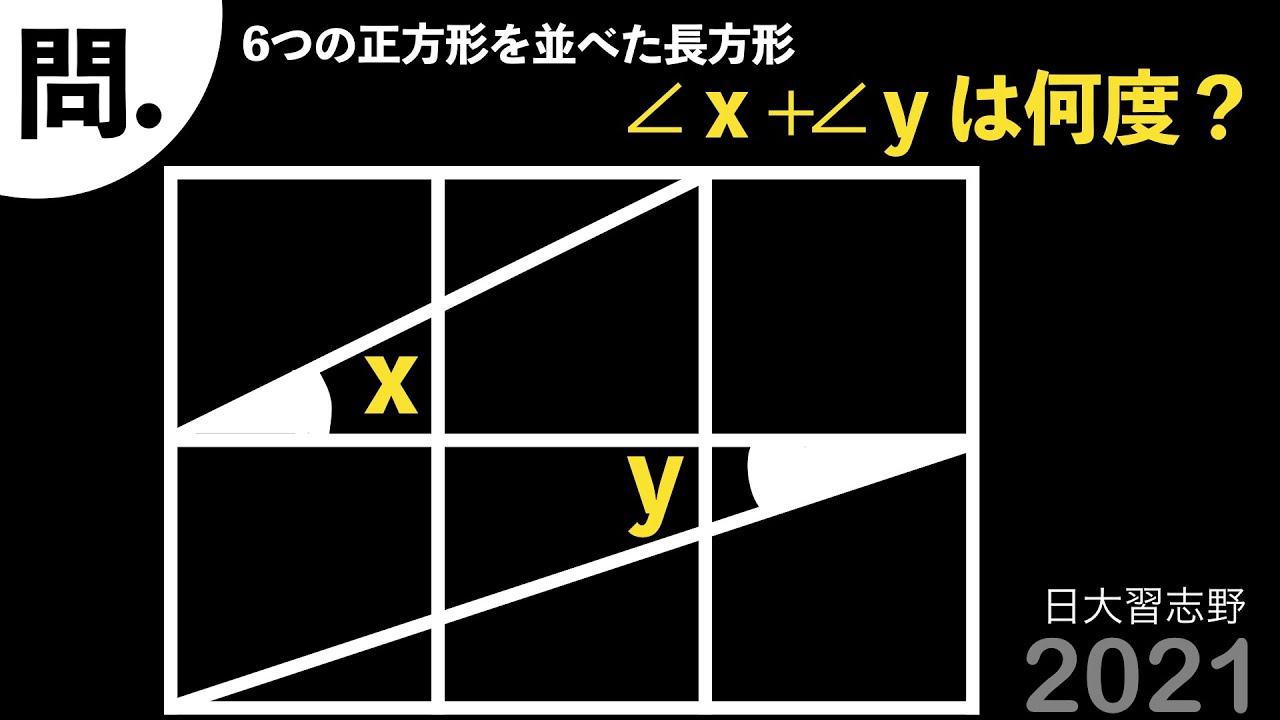
2021 日大習志野 角の和
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
6つの正方形を並べた長方形
$\angle x + \angle y = ?$
2021日本大学習志野高等学校
この動画を見る
6つの正方形を並べた長方形
$\angle x + \angle y = ?$
2021日本大学習志野高等学校
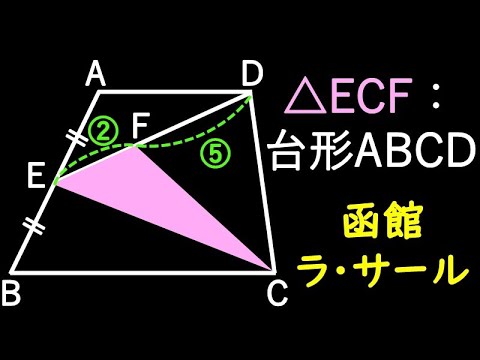
函館ラ・サール 面積比
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ECF:台形ABCD=?
*図は動画内参照
函館ラ・サール高等学校
この動画を見る
△ECF:台形ABCD=?
*図は動画内参照
函館ラ・サール高等学校
斜めの正方形 B 風車
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
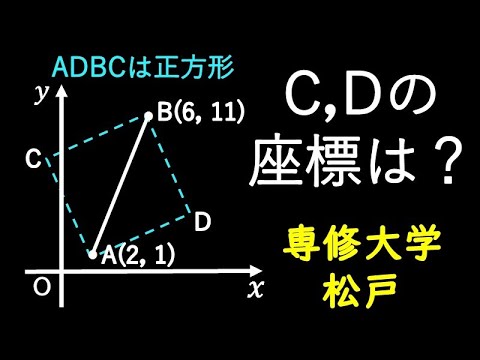
ADBCは正方形
点Cと点Dの座標は?
*図は動画内参照
専修大学松戸高等学校
この動画を見る
ADBCは正方形
点Cと点Dの座標は?
*図は動画内参照
専修大学松戸高等学校
角度 難易度MAX
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
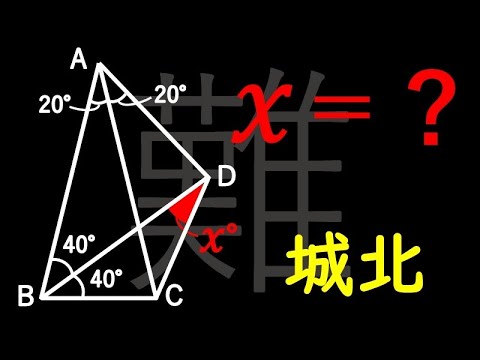
$\angle x=?$
*図は動画内参照
城北高等学校
この動画を見る
$\angle x=?$
*図は動画内参照
城北高等学校
三平方の定理?いやいや〇〇でしょ A
単元:
#数学(中学生)#中2数学#中3数学#三平方の定理#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
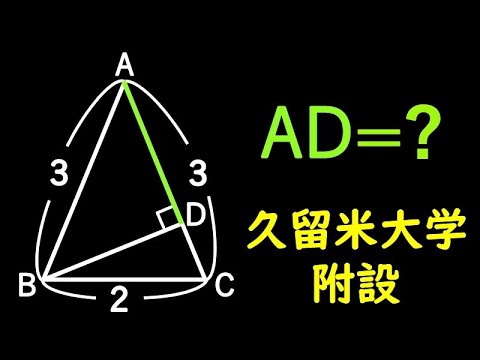
AD=?
*図は動画内参照
久留米大学附設高等学校
この動画を見る
AD=?
*図は動画内参照
久留米大学附設高等学校
【高校受験対策/数学】死守61

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#平方根#1次関数#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
この動画を見る
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
【高校受験対策/数学】図形-37

単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形37
Q
右の図は、$AB=$$\sqrt{3}$ cm、$BC=3$ cmの平行四辺形$ABCD$である。
辺$AD$上に$AE=1$ cmとなる点$E$をとり、線分$BD$と線分$CE$の交点を$F$とするとき、次の各問いに答えなさい。
問1
$△ABE$と$△CBD$が相似になることを次のように証明した。
(あ)には角、(い)には数、(う)には辺、(え)にはことばをそれぞれ入れなさい。
【証明】
$△ABE$と$△CBD$について
仮定より$\angle BAE=$ (あ) ・・・①
また$AE:CD=1:$ (い) ・・・➁
$AB:$ (う) $=\sqrt{3}:3$
$=1:$ (い) ・・・③
➁、③から
$AE:CD=AB:$ (う) ・・・④
①、④から、2組の辺の(え)とその間の角がそれぞれ等しいので
$\triangle ABE \backsim \triangle CBD$
問2
$△BCF$の面積は$△ABE$の面積の何倍か求めなさい。
この動画を見る
高校受験対策・図形37
Q
右の図は、$AB=$$\sqrt{3}$ cm、$BC=3$ cmの平行四辺形$ABCD$である。
辺$AD$上に$AE=1$ cmとなる点$E$をとり、線分$BD$と線分$CE$の交点を$F$とするとき、次の各問いに答えなさい。
問1
$△ABE$と$△CBD$が相似になることを次のように証明した。
(あ)には角、(い)には数、(う)には辺、(え)にはことばをそれぞれ入れなさい。
【証明】
$△ABE$と$△CBD$について
仮定より$\angle BAE=$ (あ) ・・・①
また$AE:CD=1:$ (い) ・・・➁
$AB:$ (う) $=\sqrt{3}:3$
$=1:$ (い) ・・・③
➁、③から
$AE:CD=AB:$ (う) ・・・④
①、④から、2組の辺の(え)とその間の角がそれぞれ等しいので
$\triangle ABE \backsim \triangle CBD$
問2
$△BCF$の面積は$△ABE$の面積の何倍か求めなさい。
図形:香川県高校入試~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)#香川県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 香川県の高校
図のような正方形$ABCD$がある。
辺$CD$上に、点$E$($2$点$C, D$と異なる)。
→点$B$と点$E$を結ぶ。
線分$BE$上に、$AB=AF$となる点$F$
(点$B$と異なる)。
→点$A$と点$F$を結ぶ。
$\angle DAF=40°$であるとき、
$\angle EBC$の大きさは何度か求めよ。
※図は動画内参照
この動画を見る
入試問題 香川県の高校
図のような正方形$ABCD$がある。
辺$CD$上に、点$E$($2$点$C, D$と異なる)。
→点$B$と点$E$を結ぶ。
線分$BE$上に、$AB=AF$となる点$F$
(点$B$と異なる)。
→点$A$と点$F$を結ぶ。
$\angle DAF=40°$であるとき、
$\angle EBC$の大きさは何度か求めよ。
※図は動画内参照
【中学数学】四角形の性質まとめ~ゲーム感覚で覚えようぜ~

角の二等分線+平行、垂直=?
単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
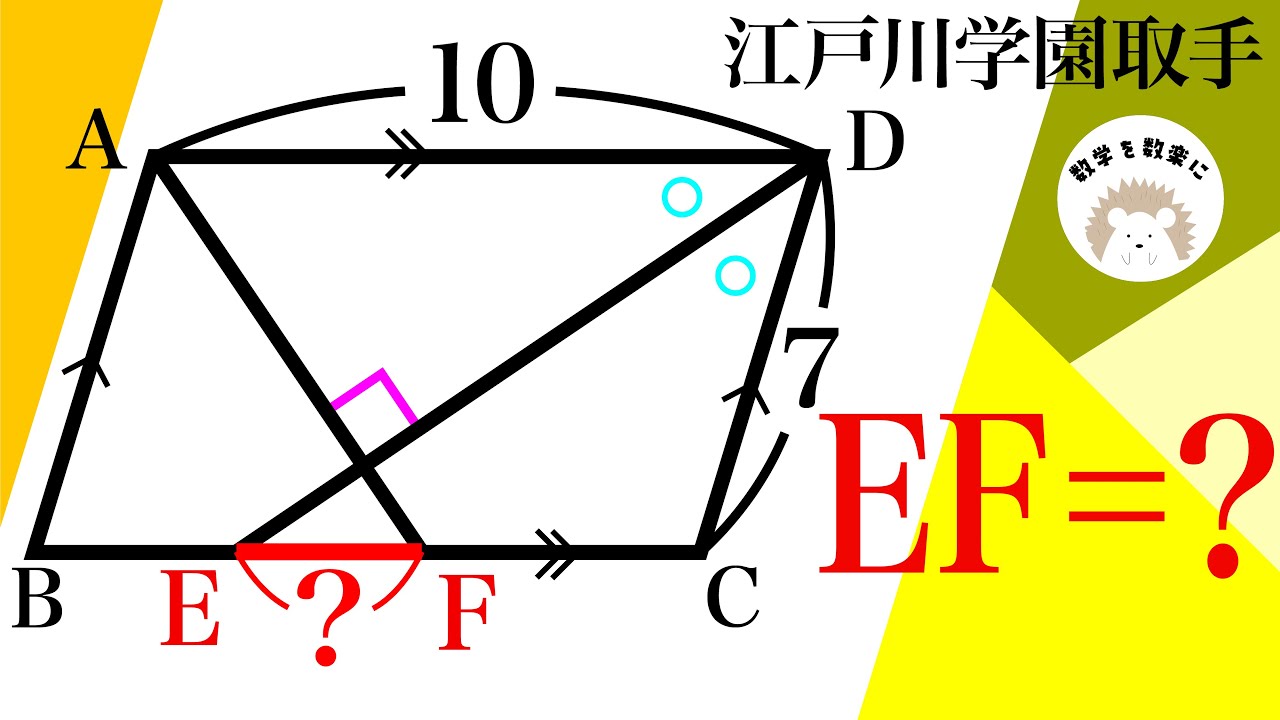
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
この動画を見る
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
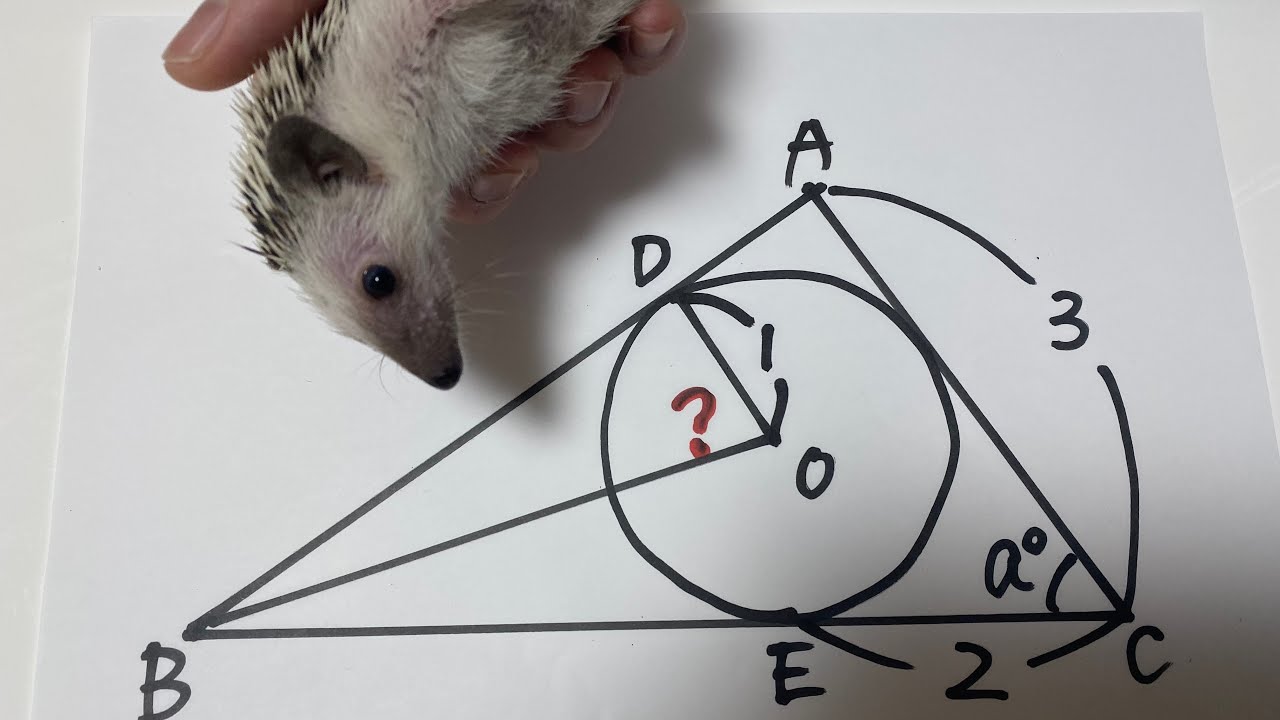
角度を求める(2006国立高校)
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、?の角度を求めよ。
出典:2006年国立高校
この動画を見る
動画内の図を参照し、?の角度を求めよ。
出典:2006年国立高校
