 中2数学
中2数学
 中2数学
中2数学
中2数学「二等辺三角形を使った合同証明」【毎日配信】

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~二等辺三角形を使った合同証明~
例題 右の図の△ABCは、AB=ACの二等辺三角形です。辺AB上に点D、辺AC上に点EをBD=CEとなるようにとると、△CDB≡△BECであることを証明しなさい。
※図は動画内参照
この動画を見る
中2~二等辺三角形を使った合同証明~
例題 右の図の△ABCは、AB=ACの二等辺三角形です。辺AB上に点D、辺AC上に点EをBD=CEとなるようにとると、△CDB≡△BECであることを証明しなさい。
※図は動画内参照
福田の数学〜京都大学2023年理系第6問〜チェビシェフの多項式と論証(PART2)

単元:
#式の計算(単項式・多項式・式の四則計算)#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#その他#推理と論証#推理と論証#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
【上手く数え上げるために…!】確率:法政大学国際高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
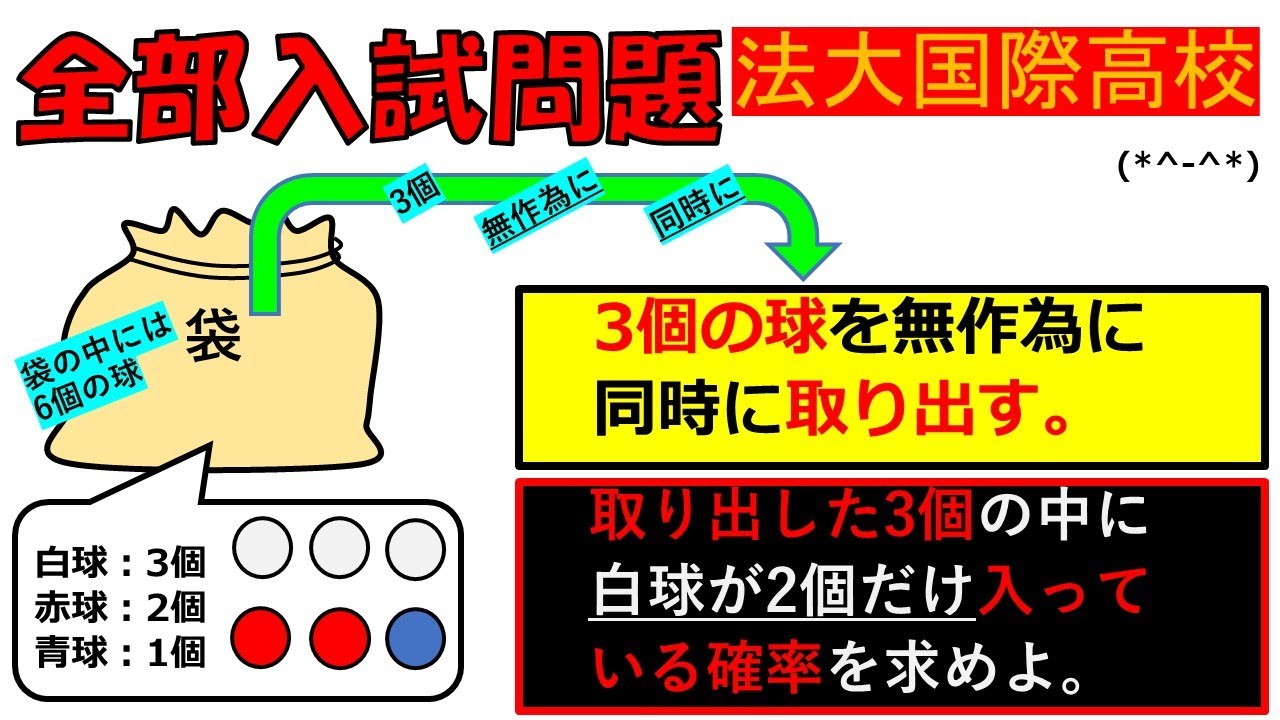
袋の中に白球が3個,赤球が2個,青球が1個の計6個の球がある.
この袋の中から3個の球を無作為に同時に取り出す.
取り出した3個の中に白球が2個だけ入っている確率を求めよ.
法大国際高校過去問
この動画を見る
袋の中に白球が3個,赤球が2個,青球が1個の計6個の球がある.
この袋の中から3個の球を無作為に同時に取り出す.
取り出した3個の中に白球が2個だけ入っている確率を求めよ.
法大国際高校過去問
福田の数学〜京都大学2023年理系第6問〜チェビシェフの多項式と論証(PART1)

単元:
#式の計算(単項式・多項式・式の四則計算)#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#その他#推理と論証#推理と論証#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{6}$ pを3以上の素数とする。また、θを実数とする。
(1)$\cos3\theta$と$\cos4\theta$を$\cos\theta$の式として表せ。
(2)$\cos\theta$=$\frac{1}{p}$のとき、θ=$\frac{m}{n}$・$\pi$となるような正の整数m,nが存在するか否かを理由をつけて判定せよ。
チェビシェフの多項式
$\cos n\theta$=$T_n$($\cos\theta$)を満たすn次の多項式$T_n(x)$が存在し、その係数はすべて整数であり、最高次の係数が$2^{n-1}$である。
これが、すべての自然数nについて成り立つことを数学的帰納法で証明せよ。
2023京都大学理系過去問
【ひと工夫で簡単に解ける…!】連立方程式:東京工業大学附属科学技術高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
1001x+999y=1007 \\
999x+1001y=993
\end{array}
\right.
\end{eqnarray}$
東工大科技高校過去問
この動画を見る
次の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
1001x+999y=1007 \\
999x+1001y=993
\end{array}
\right.
\end{eqnarray}$
東工大科技高校過去問
筆算なしで!

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
$1428 \times 1572 - 428 \times 572$ =
この動画を見る
$1428 \times 1572 - 428 \times 572$ =
式の値 ラ・サール 2023
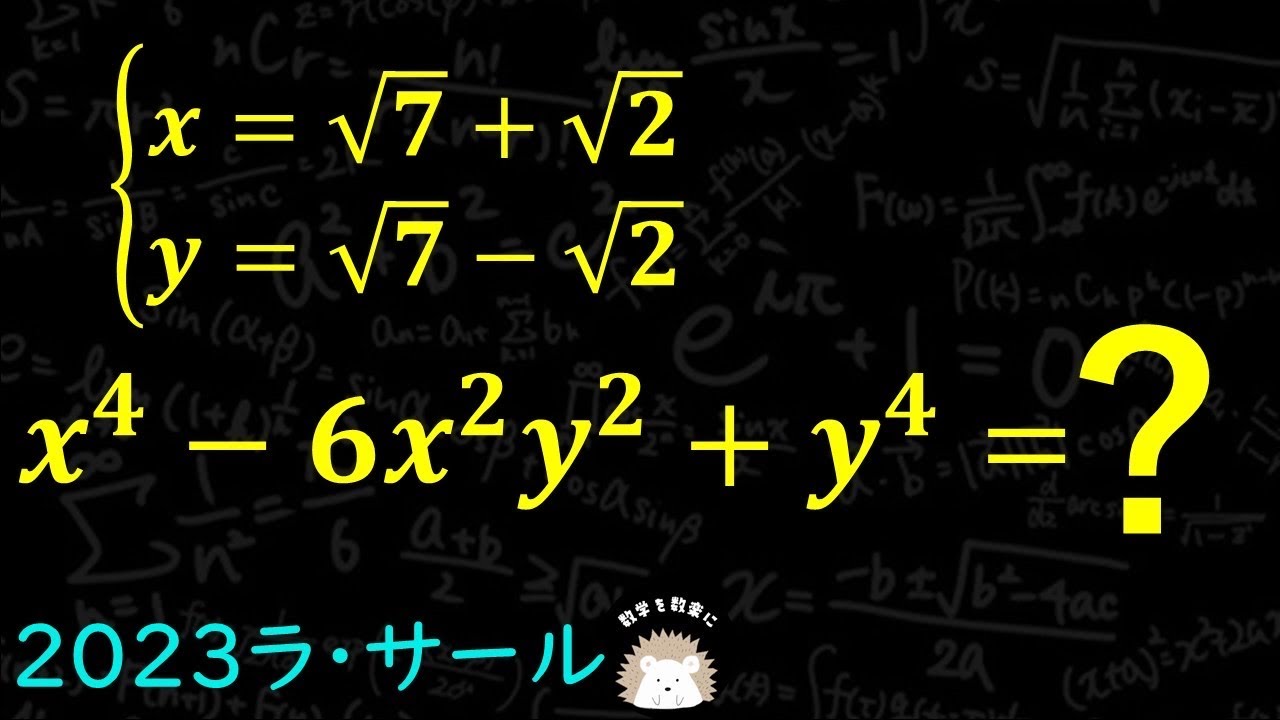
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
x = \sqrt 7 + \sqrt 2 \\
y = \sqrt 7 - \sqrt 2
\end{array}
\right.
\end{eqnarray}
$x^4 - 6x^2y^2 +y^4 = ?$
2023ラ・サール学園
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
x = \sqrt 7 + \sqrt 2 \\
y = \sqrt 7 - \sqrt 2
\end{array}
\right.
\end{eqnarray}
$x^4 - 6x^2y^2 +y^4 = ?$
2023ラ・サール学園
【分かっていても手間はかかる】連立方程式:東大寺学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
x,yについての連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
この動画を見る
x,yについての連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
高等学校入学試験予想問題:三重県公立高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
【ポイントを抑えて完答せよ…!】三平方の定理:大阪教育大学附属高等学校池田校舎~全国入試問題解法
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
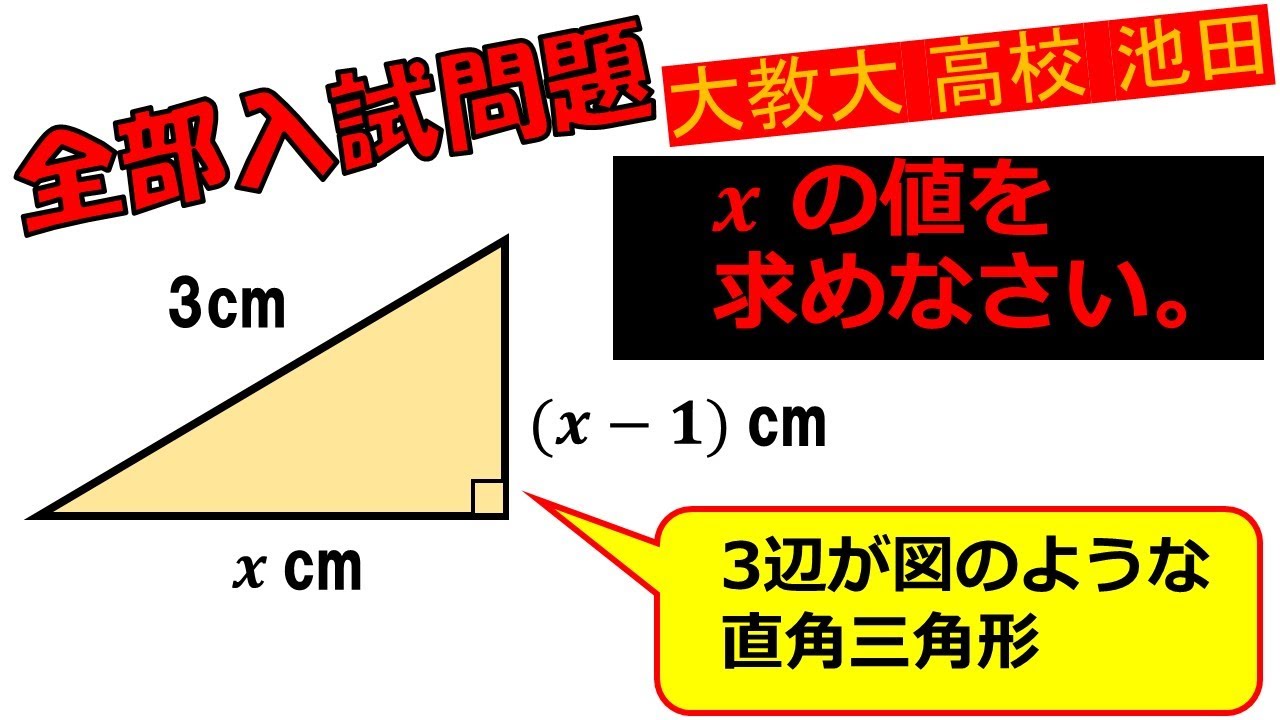
3辺が図のような直角三角形のxの値を求めなさい.
大教大高校池野過去問
この動画を見る
3辺が図のような直角三角形のxの値を求めなさい.
大教大高校池野過去問
2023高校入試数学解説87問目 展開図から組み立てる 埼玉県学校選択問題(改)

単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3つの合同な台形と2つの相似な正三角形
組み立てた立体の頂点の数は?
辺の数は?
辺ABとねじれの位置になる辺の数は?
*図は動画内参照
2023埼玉県
この動画を見る
3つの合同な台形と2つの相似な正三角形
組み立てた立体の頂点の数は?
辺の数は?
辺ABとねじれの位置になる辺の数は?
*図は動画内参照
2023埼玉県
2023高校入試数学解説84問目 一次関数と二次関数 埼玉県学校選択問題
単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
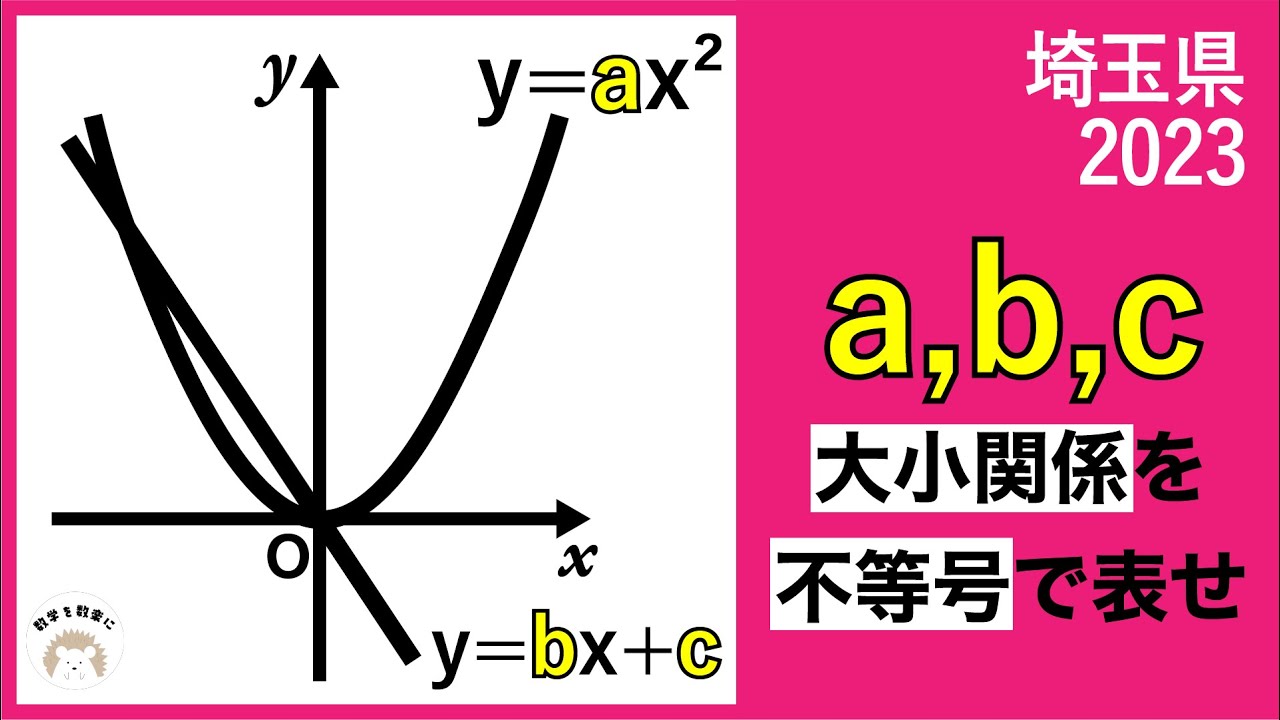
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
この動画を見る
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
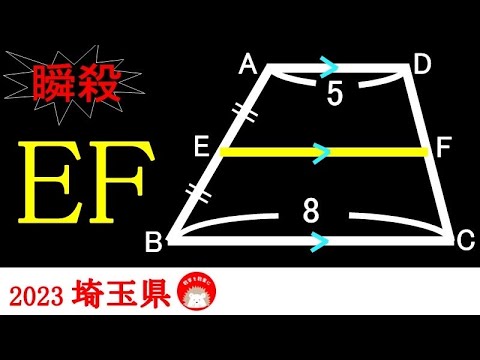
2023高校入試数学解説82問目 気付けば一瞬!!台形 埼玉県
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
EF=?
*図は動画内参照
2023埼玉県
この動画を見る
EF=?
*図は動画内参照
2023埼玉県
高等学校入学試験予想問題:秋田県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#相似な図形#文章題#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
この動画を見る
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
2023高校入試数学解説72問目 玉の取り出し 確率 東京都

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
赤玉1コ、白玉1コ、青玉4コが入った袋の中から同時に2コ取り出すとき2コとも青玉である確率は?
2023東京都共通
この動画を見る
赤玉1コ、白玉1コ、青玉4コが入った袋の中から同時に2コ取り出すとき2コとも青玉である確率は?
2023東京都共通
高等学校入学試験予想問題:鳥取県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#平面図形#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
2023高校入試数学解説63問目 分母が文字の連立方程式 城北高校
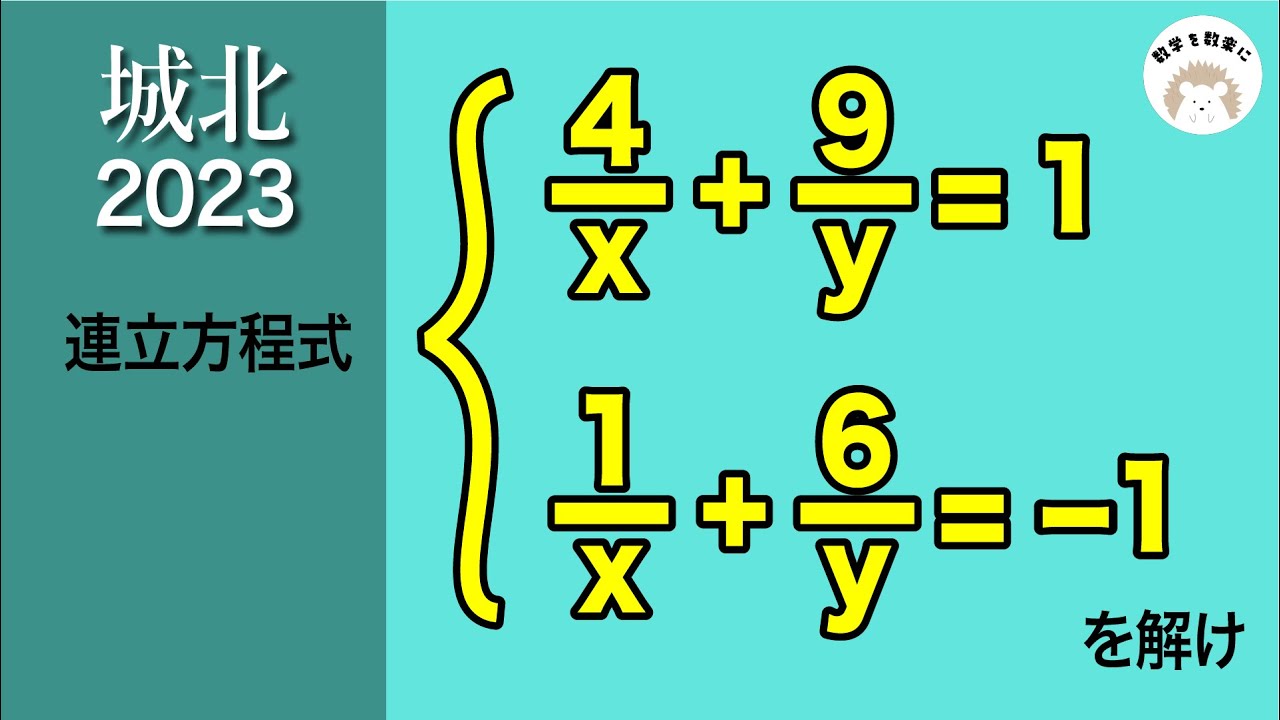
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{4}{x} + \frac{9}{y} = 1 \\
\frac{1}{x} + \frac{6}{y} = -1
\end{array}
\right.
\end{eqnarray}
2023城北学園高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{4}{x} + \frac{9}{y} = 1 \\
\frac{1}{x} + \frac{6}{y} = -1
\end{array}
\right.
\end{eqnarray}
2023城北学園高等学校
連立方程式の応用問題を難なく解く動画~全国入試問題解法 #shorts #数学 #高校受験 #過去問

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=14 \\
ax+by=3
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
bx-ay=-5 \\
4x-5y=11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき,$ a,b $の値をそれぞれ求めなさい.
巣鴨高校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=14 \\
ax+by=3
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
bx-ay=-5 \\
4x-5y=11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき,$ a,b $の値をそれぞれ求めなさい.
巣鴨高校過去問
【高校数学】これが京大の入試問題!?中学生でも解けます #Shorts
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
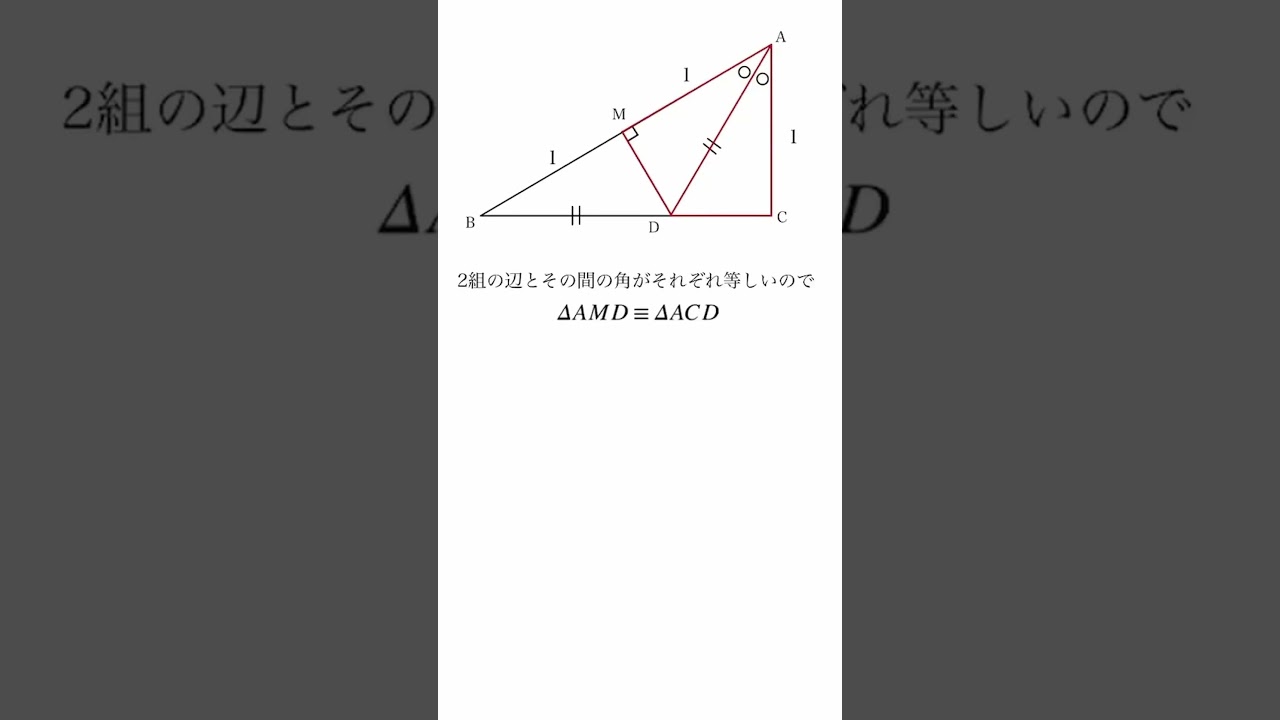
$\triangle ABC$において、$AB=2,AC=1$とする。
$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。
$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
この動画を見る
$\triangle ABC$において、$AB=2,AC=1$とする。
$\angle BAC$の二等分線と辺$BC$の交点を$D$とする。
$AD=BD$となるとき、$\triangle ABC$の面積を求めよ。
2023高校入試数学解説55問目 3つのサイコロ 明治学院

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1つのサイコロを3回投げる
出た目の数=$x_1,x_2,x_3$
下の式を満たす確率は?
(1)$(x_1 -3 )^2 +(x_2 -3 )^2 + (x_3 -3 )^2 = 0$
(2)$(x_1 -3 )^2 +(x_2 -3 )^2 + (x_3 -3 )^2 \geqq 2$
2023明治学院高等学校
この動画を見る
1つのサイコロを3回投げる
出た目の数=$x_1,x_2,x_3$
下の式を満たす確率は?
(1)$(x_1 -3 )^2 +(x_2 -3 )^2 + (x_3 -3 )^2 = 0$
(2)$(x_1 -3 )^2 +(x_2 -3 )^2 + (x_3 -3 )^2 \geqq 2$
2023明治学院高等学校
佐賀県立高校入試2021年「確率」
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年「確率」
-----------------
【ルール】
大小2つのさいころを同時に1回投げ、大きいさいころの出た目の数を十の位の数、小さいさいころの出た目の数を一の位の数としてけたの整数をつくる
このとき、下記の各問いに答えなさい。
ただし、(ルール)にある大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。
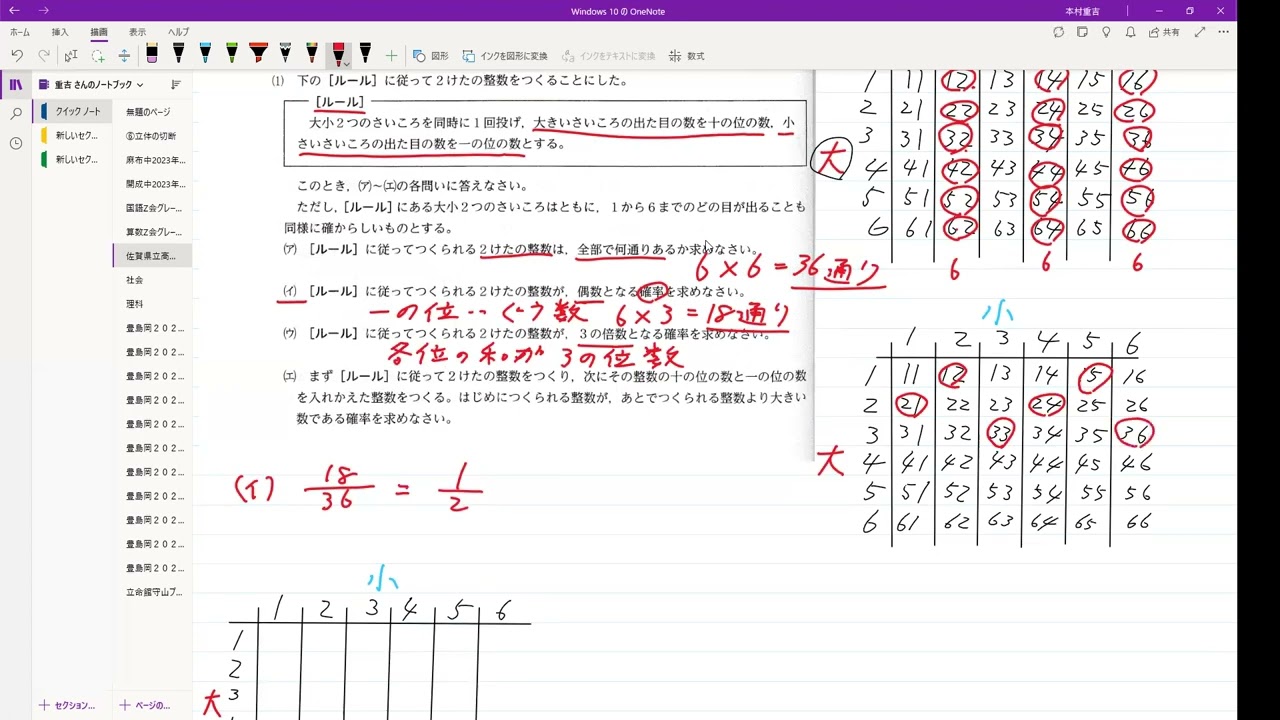
(ア)【ルール】に従ってつくられる2けたの整数は、全部で何通りあるか求めなさい。
(イ)【ルール】に従ってつくられる2けたの整数が、偶数となる確率を求めなさい。
(ウ)【ルール】に従ってつくられる2けたの整数が、3の倍数となる確率を求めなさい。
(エ)まず【ルール】に従ってだけたの整数をつくり、次にその整数の十の位の数と一の位の数を入れかえた整数をつくる。
はじめにつくられる整数が、あとでつくられる整数より大きい数である確率を求めなさい。
この動画を見る
佐賀県立高校入試2021年「確率」
-----------------
【ルール】
大小2つのさいころを同時に1回投げ、大きいさいころの出た目の数を十の位の数、小さいさいころの出た目の数を一の位の数としてけたの整数をつくる
このとき、下記の各問いに答えなさい。
ただし、(ルール)にある大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。
(ア)【ルール】に従ってつくられる2けたの整数は、全部で何通りあるか求めなさい。
(イ)【ルール】に従ってつくられる2けたの整数が、偶数となる確率を求めなさい。
(ウ)【ルール】に従ってつくられる2けたの整数が、3の倍数となる確率を求めなさい。
(エ)まず【ルール】に従ってだけたの整数をつくり、次にその整数の十の位の数と一の位の数を入れかえた整数をつくる。
はじめにつくられる整数が、あとでつくられる整数より大きい数である確率を求めなさい。
2023高校入試解説33問目 最初の一問目の計算 中大杉並

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$2021 \times 2020 - 2020 \times 2019 + 2021 \times 2022 -2022 \times 2023$
2023中央大学杉並高等学校
この動画を見る
$2021 \times 2020 - 2020 \times 2019 + 2021 \times 2022 -2022 \times 2023$
2023中央大学杉並高等学校
佐賀県立高校入試2021年2⃣連立方程式
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年2⃣連立方程式
-----------------
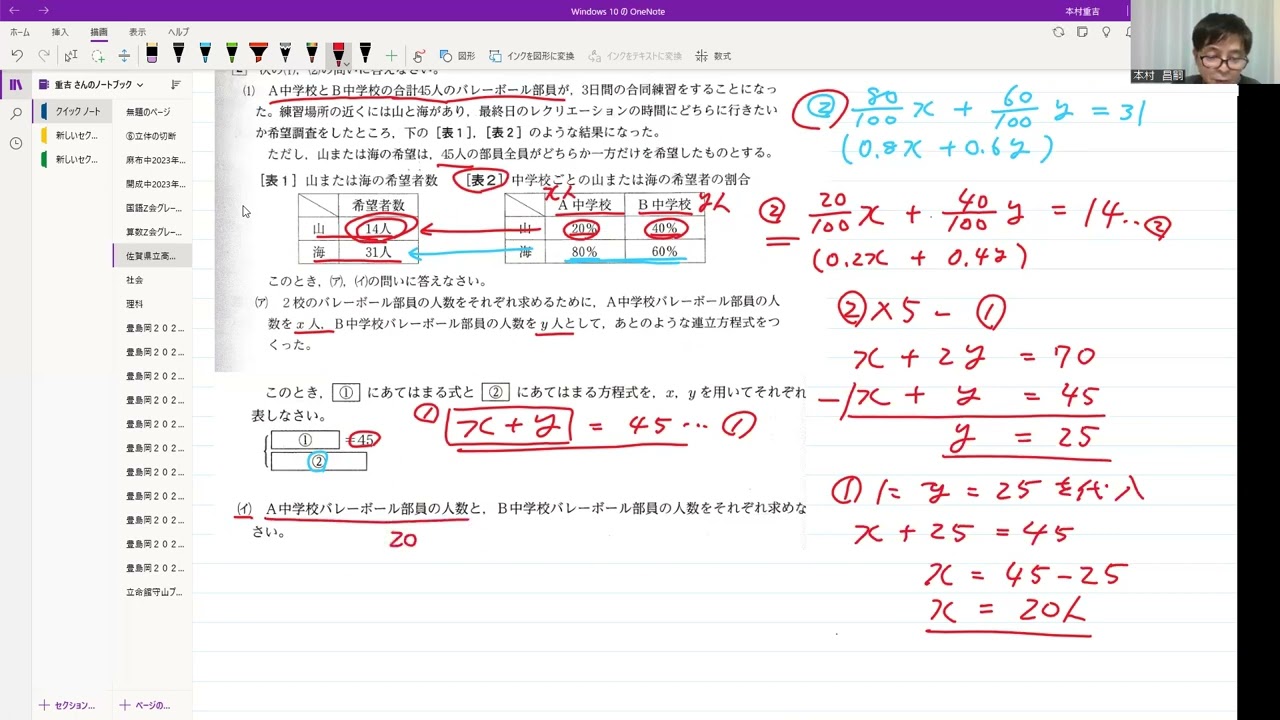
A中学校とB中学校の合計45人のバレーボール部員が、3日間の合同練習をすることになった。
練習場所の近くには山と海があり、最終日のレクリエーションの時間にどちらに行きたいか希望調査をしたところ、動画内の表のような結果になった。
ただし、山または海の希望は、45人の部員全員がどちらか一方だけを希望したものとする。
(ア)
2校のバレーボール部員の人数をそれぞれ求めるために、A中学校バレーボール部員の人数を$x$人、B中学校バレーボール部員の人数を$y$人として、あとのような連立方程式をつくった。
このとき、①にあてはまる式と②にあてはまる方程式を、$x,y$を用いてそれぞれ表しなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
① = 45 \\
②
\end{array}
\right.
\end{eqnarray}$
(イ)
A中学校バレーボール部員の人数と、B中学校バレーボール部員の人数をそれぞれ求めなさい。
この動画を見る
佐賀県立高校入試2021年2⃣連立方程式
-----------------
A中学校とB中学校の合計45人のバレーボール部員が、3日間の合同練習をすることになった。
練習場所の近くには山と海があり、最終日のレクリエーションの時間にどちらに行きたいか希望調査をしたところ、動画内の表のような結果になった。
ただし、山または海の希望は、45人の部員全員がどちらか一方だけを希望したものとする。
(ア)
2校のバレーボール部員の人数をそれぞれ求めるために、A中学校バレーボール部員の人数を$x$人、B中学校バレーボール部員の人数を$y$人として、あとのような連立方程式をつくった。
このとき、①にあてはまる式と②にあてはまる方程式を、$x,y$を用いてそれぞれ表しなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
① = 45 \\
②
\end{array}
\right.
\end{eqnarray}$
(イ)
A中学校バレーボール部員の人数と、B中学校バレーボール部員の人数をそれぞれ求めなさい。
【数学】確率の求め方間違っていませんか?確率の前提の話 後編

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
この動画を見る
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
慣れれば暗算!!

【数学】確率の求め方間違っていませんか?確率の前提の話 前編

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
大小二つのサイコロを振った時、目の合計が3になる確率は?
二つのサイコロを振った時、目の合計が3になる確率は?
答えに違いはある??
この動画を見る
確率の求め方で、間違った数え方していませんか?
確率の計算方法について解説します。
大小二つのサイコロを振った時、目の合計が3になる確率は?
二つのサイコロを振った時、目の合計が3になる確率は?
答えに違いはある??
【中学数学】直角三角形の合同条件~どこよりも分かりやすく~【中2数学】

効率よく計算するための一歩を踏み出す問題~全国入試問題解法 #shorts #数学 #高校入試 #sound

単元:
#計算と数の性質#いろいろな計算#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 26\times 78\times(-5)^2 $を計算せよ.
広大付属高校過去問
この動画を見る
$ 26\times 78\times(-5)^2 $を計算せよ.
広大付属高校過去問
高等学校入学試験予想問題:洛南高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#1次関数#2次関数#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
高校入試の早解きルートを30秒でモノにするショート~全国入試問題解法 #Shorts #数学 #高校入試
単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
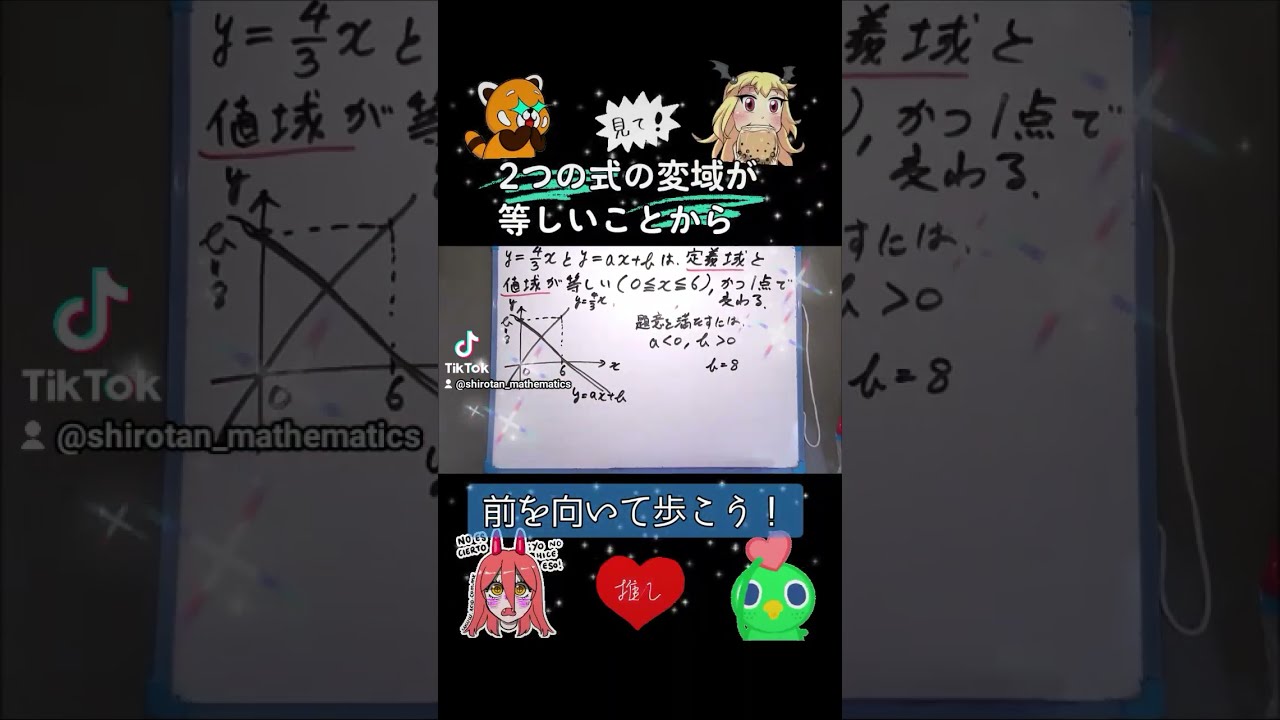
xの変域が$ o\leqq x \leqq 6 $のとき,yの変域が等しく,この関数のグラフは1点で交わる.
この交点を反比例$ y=\dfrac{c}{x}$のグラフが通るとき,$ c $の値を求めよ.
和洋国府台女子高校過去問
この動画を見る
xの変域が$ o\leqq x \leqq 6 $のとき,yの変域が等しく,この関数のグラフは1点で交わる.
この交点を反比例$ y=\dfrac{c}{x}$のグラフが通るとき,$ c $の値を求めよ.
和洋国府台女子高校過去問
