2次関数
2次関数
【高校受験対策】数学－死守１７
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#２次方程式#確率#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問いに答えなさい.
①$6-2\times (-5)$を計算しなさい.
②$\dfrac{1}{3}-\dfrac{7}{9}$を計算しなさい.
③$2(a+3b)-(a-4b)$を計算しなさい.
④$\sqrt8+\dfrac{6}{\sqrt2}$を計算しなさい.
⑤2次方程式$x^2+2x-15=0$を計算しなさい.
⑥赤,白,青の棒が各1本ずつ箱の中に入っている.
この3本の棒をよく混ぜて1本取り出し,色を確認してからもとにもどします.
このことを2回行うとき,確認した色が2回とも赤か,
2回とも白になる確率を求めなさい.
⑦相似な2つの立体$P,Q$があり,その表面積の比は$4:9$です.
立体$P$の体積が$8cm^3$のとき,立体$Q$の体積を求めなさい.
⑧図1のように,関数$y = ax^2$グラフ上に,$x$座標が-1となる点をとります.
また,$x$軸上の,座標が$ (1,0)$となる点を$B$とします.
直線$AB$の切片が2のとき,$a$の値を求めなさい.
⑨図2のように,直線$\ell$,2点$A,B$があります.
直線$\ell$上にあって,2点$A,B$から等しい距離にある点$P$を,
作図によって求めなさい.
なお,作図に用いた線は消さずに残しなさい.
図は動画内参照
この動画を見る
次の各問いに答えなさい.
①$6-2\times (-5)$を計算しなさい.
②$\dfrac{1}{3}-\dfrac{7}{9}$を計算しなさい.
③$2(a+3b)-(a-4b)$を計算しなさい.
④$\sqrt8+\dfrac{6}{\sqrt2}$を計算しなさい.
⑤2次方程式$x^2+2x-15=0$を計算しなさい.
⑥赤,白,青の棒が各1本ずつ箱の中に入っている.
この3本の棒をよく混ぜて1本取り出し,色を確認してからもとにもどします.
このことを2回行うとき,確認した色が2回とも赤か,
2回とも白になる確率を求めなさい.
⑦相似な2つの立体$P,Q$があり,その表面積の比は$4:9$です.
立体$P$の体積が$8cm^3$のとき,立体$Q$の体積を求めなさい.
⑧図1のように,関数$y = ax^2$グラフ上に,$x$座標が-1となる点をとります.
また,$x$軸上の,座標が$ (1,0)$となる点を$B$とします.
直線$AB$の切片が2のとき,$a$の値を求めなさい.
⑨図2のように,直線$\ell$,2点$A,B$があります.
直線$\ell$上にあって,2点$A,B$から等しい距離にある点$P$を,
作図によって求めなさい.
なお,作図に用いた線は消さずに残しなさい.
図は動画内参照
【高校受験対策】数学－死守１５
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#空間図形#確率#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問に答えなさい.
①$6x-x$を計算しなさい.
②$6+(-2)\times 4$を計算しなさい.
③$\sqrt{45}-2\sqrt5$を計算しなさい.
④$x=18$のとき,
$x^2-6x-16$の値を求めなさい.
⑤2次方程式$3x^2+7x+1=0$を解きなさい.
⑥連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=18 \\
x+y=7
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦関数$y=\dfrac{1}{2}x^2$の値が1から5まで増加するときの変化の割合が,
一次関数$y = ax + 2$ の変化の割合と等しくなりました.
$a$の値を求めなさい.
⑧図1のような円錐の形のチョコレートがあります.
このチョコレートの8分の1の量をもらえることになり,
底面と平行に切って頂点のあるほうをもらうことにしました.
母線の長さを$8cm$とすると,
頂点から母線にそって何$cm$のところを切ればよいかを求めなさい.
⑨図2で,$\angle A=48$の$△ABC$があり,$\angle B,\angle C$の
二等分線をそれぞれかいたときの交点を$D$とします.
このとき,$\angle BDC$の大きさを求めなさい.
➉図3のように,円周上に18個の点が等間隔に並んでおり,
そのうちの点を$P$とします.
1個の黒石を点$P$上に置き,この黒石を,
1から6までの目が出るさいころを1回投げるごとに,
出た目の数だけ円周上の点上を順に動かします.
動かし方は,偶数の目が出たときは右回りに,
奇数の目が出たときは左回りに動かすものとします.
さいころを3回投げたとき,黒石が点$P$に戻っている確率を求めなさい.
図は動画内を参照
この動画を見る
次の各問に答えなさい.
①$6x-x$を計算しなさい.
②$6+(-2)\times 4$を計算しなさい.
③$\sqrt{45}-2\sqrt5$を計算しなさい.
④$x=18$のとき,
$x^2-6x-16$の値を求めなさい.
⑤2次方程式$3x^2+7x+1=0$を解きなさい.
⑥連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=18 \\
x+y=7
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦関数$y=\dfrac{1}{2}x^2$の値が1から5まで増加するときの変化の割合が,
一次関数$y = ax + 2$ の変化の割合と等しくなりました.
$a$の値を求めなさい.
⑧図1のような円錐の形のチョコレートがあります.
このチョコレートの8分の1の量をもらえることになり,
底面と平行に切って頂点のあるほうをもらうことにしました.
母線の長さを$8cm$とすると,
頂点から母線にそって何$cm$のところを切ればよいかを求めなさい.
⑨図2で,$\angle A=48$の$△ABC$があり,$\angle B,\angle C$の
二等分線をそれぞれかいたときの交点を$D$とします.
このとき,$\angle BDC$の大きさを求めなさい.
➉図3のように,円周上に18個の点が等間隔に並んでおり,
そのうちの点を$P$とします.
1個の黒石を点$P$上に置き,この黒石を,
1から6までの目が出るさいころを1回投げるごとに,
出た目の数だけ円周上の点上を順に動かします.
動かし方は,偶数の目が出たときは右回りに,
奇数の目が出たときは左回りに動かすものとします.
さいころを3回投げたとき,黒石が点$P$に戻っている確率を求めなさい.
図は動画内を参照
【高校受験対策】数学－関数２６
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図1で,点$O$は原点,直線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフを表している.
点$A$,点$B$はともに曲線上にあり,$x$座標はそれぞれ$-4,2$である.
曲線上にある点を$P$とする.このとき,次の各問いに答えよ.
$\boxed{問1}$
点$P$の$y$座標を$a$とする.
点$P$が点$A$から点$B$まで動くとき,
$a$のとる値の範囲を不等号を使って,$\Box \leqq a \leqq \Box$で表せ.
$\boxed{問2}$
右の図2は,図1において,点$P$を通り傾き$-\dfrac{1}{2}$の直線を引き,
$y$軸との交点を$Q$とした場合を表している.
次の①,②に答えよ.
①異なる2点$A,P$を通る直線が$x$軸と平行になるとき,
2点$A,Q$を通る直線の式を求めよ.
②点$P$の$x$座標が2より大きい数であるとき,
点$A$と点$B$,点$A$と点$Q$,点$B$と点$Q$をそれぞれ結んだ場合を考える.
$△ABQ$の面積が30のとき,点$P$の座標を求めよ.
図は動画内を参照
この動画を見る
右の図1で,点$O$は原点,直線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフを表している.
点$A$,点$B$はともに曲線上にあり,$x$座標はそれぞれ$-4,2$である.
曲線上にある点を$P$とする.このとき,次の各問いに答えよ.
$\boxed{問1}$
点$P$の$y$座標を$a$とする.
点$P$が点$A$から点$B$まで動くとき,
$a$のとる値の範囲を不等号を使って,$\Box \leqq a \leqq \Box$で表せ.
$\boxed{問2}$
右の図2は,図1において,点$P$を通り傾き$-\dfrac{1}{2}$の直線を引き,
$y$軸との交点を$Q$とした場合を表している.
次の①,②に答えよ.
①異なる2点$A,P$を通る直線が$x$軸と平行になるとき,
2点$A,Q$を通る直線の式を求めよ.
②点$P$の$x$座標が2より大きい数であるとき,
点$A$と点$B$,点$A$と点$Q$,点$B$と点$Q$をそれぞれ結んだ場合を考える.
$△ABQ$の面積が30のとき,点$P$の座標を求めよ.
図は動画内を参照
【高校受験対策】数学－死守１４
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#2次関数#円#表とグラフ#表とグラフ・集合#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問いに答えなさい.
①$(2x - 1) - 5(x + 1)$ を計算しなさい.
②1次方程式$x-6=\dfrac{x}{4}$を計算しなさい.
③ $(- 6ab)^2 \div (- 9ab^2)$を計算しなさい.
④連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=10 \\
4x-y=-8
\end{array}
\right.
\end{eqnarray}$
⑤$(2\sqrt{10}- 5)(\sqrt{10} + 4)$を計算しなさい.
⑥2次方程式 $2x^2 - 3x - 1 = 0$を解きなさい.
⑦関数$y=2x^2$について,$x$の変域が$a\leqq x\leqq 1$のとき,
$y$の変域は$0\leqq y \leqq 18$である.
このとき,$a$の値を答えなさい.
⑧図1のように,$△ABC$の2辺$AB,AC$上にそれぞれ,
点$D,E$があり,$DE /\!/ BC$である.
$BC = 8cm,△ADE$と$△ABC$の面積の比が$9:16$のとき,
線分$DE$の長さを答えなさい.
⑨図2のように,円$O$の円周上に4つの点$A,B,C,D$があり,
線分$AC$は円$O$の直径である.
$\angle DAC=55°$であるとき,$\angle x$の大きさを答えなさい.
⑩右の表は,生徒37人の最近1か月間に読んだ本の冊数を調べ,
度数分布表にまとめたものである.
このとき,冊数の中央値と最頻値を,それぞれ答えなさい.
また,冊数の平均値を,小数第2位を四捨五入して,
小数第1位まで答えなさい.
図は動画内を参照
この動画を見る
次の各問いに答えなさい.
①$(2x - 1) - 5(x + 1)$ を計算しなさい.
②1次方程式$x-6=\dfrac{x}{4}$を計算しなさい.
③ $(- 6ab)^2 \div (- 9ab^2)$を計算しなさい.
④連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=10 \\
4x-y=-8
\end{array}
\right.
\end{eqnarray}$
⑤$(2\sqrt{10}- 5)(\sqrt{10} + 4)$を計算しなさい.
⑥2次方程式 $2x^2 - 3x - 1 = 0$を解きなさい.
⑦関数$y=2x^2$について,$x$の変域が$a\leqq x\leqq 1$のとき,
$y$の変域は$0\leqq y \leqq 18$である.
このとき,$a$の値を答えなさい.
⑧図1のように,$△ABC$の2辺$AB,AC$上にそれぞれ,
点$D,E$があり,$DE /\!/ BC$である.
$BC = 8cm,△ADE$と$△ABC$の面積の比が$9:16$のとき,
線分$DE$の長さを答えなさい.
⑨図2のように,円$O$の円周上に4つの点$A,B,C,D$があり,
線分$AC$は円$O$の直径である.
$\angle DAC=55°$であるとき,$\angle x$の大きさを答えなさい.
⑩右の表は,生徒37人の最近1か月間に読んだ本の冊数を調べ,
度数分布表にまとめたものである.
このとき,冊数の中央値と最頻値を,それぞれ答えなさい.
また,冊数の平均値を,小数第2位を四捨五入して,
小数第1位まで答えなさい.
図は動画内を参照
【高校受験対策】数学－関数２５
単元：
#数学(中学生)#中２数学#中３数学#1次関数#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように,
関数$y=\dfrac{12}{x}$のグラフ上を$x \gt 0$の範囲で動く
点$A,x \lt 0$の範囲で動く点$B$があります.
点$B$の$x$座標の絶対値は点$A$の$x$座標の3倍であり,
線分$AB$と$x$軸との交点を$C$とします.
また,$x$軸上に点$D(5, 0)$があります.
これについて,次の各問いに答えなさい.
①点$A$の$x$座標が2のとき,直線$AD$の式を求めなさい.
②$\triangle ABD$の面積が28となるとき,
$\triangle ACD$の面積を求めなさい.
図は動画内を参照
この動画を見る
右の図のように,
関数$y=\dfrac{12}{x}$のグラフ上を$x \gt 0$の範囲で動く
点$A,x \lt 0$の範囲で動く点$B$があります.
点$B$の$x$座標の絶対値は点$A$の$x$座標の3倍であり,
線分$AB$と$x$軸との交点を$C$とします.
また,$x$軸上に点$D(5, 0)$があります.
これについて,次の各問いに答えなさい.
①点$A$の$x$座標が2のとき,直線$AD$の式を求めなさい.
②$\triangle ABD$の面積が28となるとき,
$\triangle ACD$の面積を求めなさい.
図は動画内を参照
【高校受験対策】数学－関数２４(動画では間違って２３と書いちゃいました。汗)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で,曲線は関数$y=x^2$グラフです.
$x$軸上に $x$座標が$-3$である点$A$をとり,
点$A$を通り傾きが正の直線をひきます.
直線と曲線との交点のうちと座標が負のものを$B$,正のものを$C$とし,
直線と軸との交点を$D$とします.
このとき次の各問に答えなさい.ただし,座標軸の単位の長さを$1cm$とします.
①点$B$の$x$座標が$-2$のとき,$△BOD$の面積を求めなさい.
②$AB: BC = 1 :3$のとき,$BC$の長さを求めなさい.
図は動画内を参照
この動画を見る
右の図で,曲線は関数$y=x^2$グラフです.
$x$軸上に $x$座標が$-3$である点$A$をとり,
点$A$を通り傾きが正の直線をひきます.
直線と曲線との交点のうちと座標が負のものを$B$,正のものを$C$とし,
直線と軸との交点を$D$とします.
このとき次の各問に答えなさい.ただし,座標軸の単位の長さを$1cm$とします.
①点$B$の$x$座標が$-2$のとき,$△BOD$の面積を求めなさい.
②$AB: BC = 1 :3$のとき,$BC$の長さを求めなさい.
図は動画内を参照
【高校受験対策】数学－死守１０
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#2次関数#文章題#文章題その他#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
1.次の各問に答えなさい.
①$9a-5a$を計算しなさい.
②$12\div (-2)+1$を計算しなさい.
③$6\sqrt7-\sqrt{28}$を計算しなさい.
④$x=13$のとき,$x^2-8x+15$の値を求めなさい.
⑤2次方程式$5x^2-9x+3=0$を解きなさい.
⑥連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x - 2y = 7 \\
x + y = -1
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦右の図の曲線は,$y=ax^2$のグラフです.
グラフから,$a$の値を求めなさい.
⑧上の表は,あるクイズ大会に参加した40人全員の結果をまとめたものです.
クイズの問題は,$A,B,C$の3問ありました.
正解のときに与えられた得点は,$A,B$がそれぞれ1点,$C$が3点で,
正解のとき以外は0点でした.3問のうち2問だけが正解だった人数を求めなさい.
⑨右の図1の四角形$ABCD$は,$AD /\!/ BC$の台形であり,
線分$AC$と$DB$の交点を$E$とします.
$AB=AD,\angle BAC=80° \angle ACB = 30°$のとき,
$\angle DEC$の大きさ$x$を求めなさい.
⑩右の図2は,正四角錐の投影図です.
この正四角錐の立面図は,1辺の長さが$6cm$の正三角形です.
この正四角錐の体積を求めなさい.
⑪ある菓子店では,どら焼きを6個入りの箱と8個入りの箱で販売している.
6個入りの箱と8個入りの箱の組み合わせで,
どら焼きをちょうど34個買うには,6個入りの箱と8 個入りの箱は,
それぞれ何箱になるか求めなさい.
この動画を見る
1.次の各問に答えなさい.
①$9a-5a$を計算しなさい.
②$12\div (-2)+1$を計算しなさい.
③$6\sqrt7-\sqrt{28}$を計算しなさい.
④$x=13$のとき,$x^2-8x+15$の値を求めなさい.
⑤2次方程式$5x^2-9x+3=0$を解きなさい.
⑥連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x - 2y = 7 \\
x + y = -1
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦右の図の曲線は,$y=ax^2$のグラフです.
グラフから,$a$の値を求めなさい.
⑧上の表は,あるクイズ大会に参加した40人全員の結果をまとめたものです.
クイズの問題は,$A,B,C$の3問ありました.
正解のときに与えられた得点は,$A,B$がそれぞれ1点,$C$が3点で,
正解のとき以外は0点でした.3問のうち2問だけが正解だった人数を求めなさい.
⑨右の図1の四角形$ABCD$は,$AD /\!/ BC$の台形であり,
線分$AC$と$DB$の交点を$E$とします.
$AB=AD,\angle BAC=80° \angle ACB = 30°$のとき,
$\angle DEC$の大きさ$x$を求めなさい.
⑩右の図2は,正四角錐の投影図です.
この正四角錐の立面図は,1辺の長さが$6cm$の正三角形です.
この正四角錐の体積を求めなさい.
⑪ある菓子店では,どら焼きを6個入りの箱と8個入りの箱で販売している.
6個入りの箱と8個入りの箱の組み合わせで,
どら焼きをちょうど34個買うには,6個入りの箱と8 個入りの箱は,
それぞれ何箱になるか求めなさい.
【高校受験対策】数学－関数２３
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図において,①は関数$y=\dfrac{1}{2}x^2$,
②は$x$軸に平行な直線のグラフである.
①と②の交点のうち,$x$座標が正のものを$A$,負のものを$B$とする.
また,$C$は$x$軸上を動く点で,2点$B,C$を通る直線のグラフを③とし,
①と③のグラフの交点のうち,$B$でないほうを$P$とする.
ただし,点$C$の$x$座標は正である.
①点$A$の$x$座標が3のとき,$△OAB$の面積を求めよ.
②点$B$の$x$座標を$-4$,点$C$の$x$座標を$12$とするとき,
直線$BC$の式を求めよ.
③点$B$の$y$座標を$4$とする.
$△OPB$と$△OCP$の面積が等しいとき,
$△OCB$を$x$軸を軸として1回転させてできる
立体の体積を求めよ.
図は動画内を参照
この動画を見る
右の図において,①は関数$y=\dfrac{1}{2}x^2$,
②は$x$軸に平行な直線のグラフである.
①と②の交点のうち,$x$座標が正のものを$A$,負のものを$B$とする.
また,$C$は$x$軸上を動く点で,2点$B,C$を通る直線のグラフを③とし,
①と③のグラフの交点のうち,$B$でないほうを$P$とする.
ただし,点$C$の$x$座標は正である.
①点$A$の$x$座標が3のとき,$△OAB$の面積を求めよ.
②点$B$の$x$座標を$-4$,点$C$の$x$座標を$12$とするとき,
直線$BC$の式を求めよ.
③点$B$の$y$座標を$4$とする.
$△OPB$と$△OCP$の面積が等しいとき,
$△OCB$を$x$軸を軸として1回転させてできる
立体の体積を求めよ.
図は動画内を参照
【高校受験対策】死守－３
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#1次関数#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
この動画を見る
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
【高校受験対策】数学－関数２２
単元：
#数学(中学生)#中２数学#中３数学#1次関数#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図において,直線$\ell$は関数$y = 2x + 8$ グラフで,
曲線$m$は関数$y=ax^2$のグラフである.
点$A$は直線$\ell$と$y$軸との交点である.
点$B$は曲線$m$上の点で,その$x$座標は6であり,
線分$AB$は$x$軸に平行である.
点$C$は直線$\ell$と$x$軸との交点である.
また,原点を$O$とするとき,点$D$は$y$軸の点で,
$OB=OD$であり,その$y$座標は負である.
さらに,点$E$は$OD=BE$となる点で,線分$BE$は$y$軸に平行であり,
その$y$座標は負である.このとき,次の問いに答えなさい.
①$a$の値を求めなさい.
②直線$CD$の式を求めなさい.
③点$F$は線分$OA$の中点であり,
点$G$は線分$DE$上の点である.
直線$FG$が四角形$ODEB$の面積を2等分するとき,
点$G$の座標を求めなさい.
この動画を見る
右の図において,直線$\ell$は関数$y = 2x + 8$ グラフで,
曲線$m$は関数$y=ax^2$のグラフである.
点$A$は直線$\ell$と$y$軸との交点である.
点$B$は曲線$m$上の点で,その$x$座標は6であり,
線分$AB$は$x$軸に平行である.
点$C$は直線$\ell$と$x$軸との交点である.
また,原点を$O$とするとき,点$D$は$y$軸の点で,
$OB=OD$であり,その$y$座標は負である.
さらに,点$E$は$OD=BE$となる点で,線分$BE$は$y$軸に平行であり,
その$y$座標は負である.このとき,次の問いに答えなさい.
①$a$の値を求めなさい.
②直線$CD$の式を求めなさい.
③点$F$は線分$OA$の中点であり,
点$G$は線分$DE$上の点である.
直線$FG$が四角形$ODEB$の面積を2等分するとき,
点$G$の座標を求めなさい.
【高校受験対策】数学－関数１８
単元：
#数学(中学生)#中２数学#中３数学#1次関数#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図1のように,$AB = 8cm,\angle ABC=90°,\angle BCD = 90°$の
四角形$ABCD$がある.
点$P$は頂点$A$を出発し,
一定の速さで辺$AB,BC,CD$上を通って,頂点$D$まで移動する.
点$P$が頂点$A$を出発してから$x$秒後の3点$A,P,D$を結んでできる
$△APD$の面積を$ycm^2$とする.
右の図2は, $x$と$y$の関係をグラフに表したものである.
このとき,次の各問いに答えなさい.
ただし,点$P$が頂点$A,D$にあるときは$y=0$とする.
①点$P$が移動する速さは毎秒何$cm$か答えなさい.
②図1の辺$BC$と辺$CD$の長さをそれぞれ求めなさい.
③図2のグラフ中の$a$の値と$b$の値を,それぞれ求めなさい.
④点$P$が辺$BC$上にあるとき,
$△ABP$と$△APD$の面積が等しくなるのは,
点$P$が頂点$A$を出発してから何秒後か求めなさい.
図は動画内参照
この動画を見る
右の図1のように,$AB = 8cm,\angle ABC=90°,\angle BCD = 90°$の
四角形$ABCD$がある.
点$P$は頂点$A$を出発し,
一定の速さで辺$AB,BC,CD$上を通って,頂点$D$まで移動する.
点$P$が頂点$A$を出発してから$x$秒後の3点$A,P,D$を結んでできる
$△APD$の面積を$ycm^2$とする.
右の図2は, $x$と$y$の関係をグラフに表したものである.
このとき,次の各問いに答えなさい.
ただし,点$P$が頂点$A,D$にあるときは$y=0$とする.
①点$P$が移動する速さは毎秒何$cm$か答えなさい.
②図1の辺$BC$と辺$CD$の長さをそれぞれ求めなさい.
③図2のグラフ中の$a$の値と$b$の値を,それぞれ求めなさい.
④点$P$が辺$BC$上にあるとき,
$△ABP$と$△APD$の面積が等しくなるのは,
点$P$が頂点$A$を出発してから何秒後か求めなさい.
図は動画内参照
【受験対策】数学－関数１７
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように,関数$y=ax^2$のグラフ上に点$A$がある.
点$A$の$x$座標が2のとき,次の問いに答えなさい.
ただし,$a\gt 0$とする.
①点$A$の$y$座標が6のとき,$a$の値を求めなさい.
②$a=2$とする.
直線$y=2x+b$が点$A$をとおるとき,$b$の値を求めなさい.
③点$A$と$y$軸について,対称な点を$B$とする.
また,$y$軸上に$y$座標が$-1$となる点$C$をとる.
$\triangle ABC$が直角二等辺三角形となるとき,
$a$の値を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=ax^2$のグラフ上に点$A$がある.
点$A$の$x$座標が2のとき,次の問いに答えなさい.
ただし,$a\gt 0$とする.
①点$A$の$y$座標が6のとき,$a$の値を求めなさい.
②$a=2$とする.
直線$y=2x+b$が点$A$をとおるとき,$b$の値を求めなさい.
③点$A$と$y$軸について,対称な点を$B$とする.
また,$y$軸上に$y$座標が$-1$となる点$C$をとる.
$\triangle ABC$が直角二等辺三角形となるとき,
$a$の値を求めなさい.
図は動画内参照
【受験対策】数学－関数１６
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
この動画を見る
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
【受験対策】数学－関数１４
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
この動画を見る
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
【受験対策】数学－関数１３
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように,関数$y=x^2･･･(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=x^2･･･(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
【中１ P.128】４編の力だめし
中学数学（2次関数）【篠原好】
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
中３向け数学「２次関数」についての説明です。
※図式・数式は動画内参照
この動画を見る
中３向け数学「２次関数」についての説明です。
※図式・数式は動画内参照
【受験対策】 数学－関数⑤
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
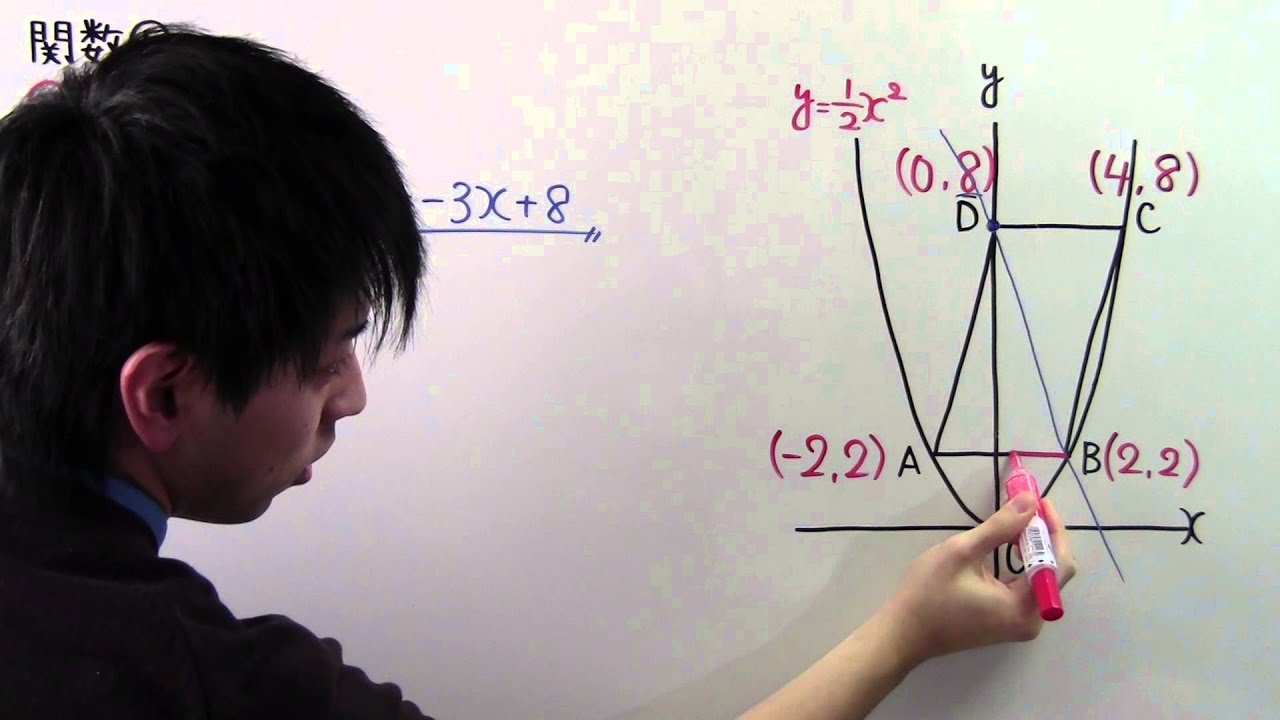
右の図のように、関数$y=\displaystyle \frac{1}{2}x^2$のグラフ上に、 3点A、B、Cがあり、
点Bのx座標は2、点Cのx座標は4である。
また、y軸上に点、D(0.8)がある。
四角形ABCDが 平行四辺形となるとき、次の問いに答えよう。
①点Aの座標は?
②直線BDの式は?
③平行四辺形ABCDの面積は?
④原点Oを通り、平行四辺形ABCDの
面積を2等分する直線の式は?
※図は動画内参照
この動画を見る
右の図のように、関数$y=\displaystyle \frac{1}{2}x^2$のグラフ上に、 3点A、B、Cがあり、
点Bのx座標は2、点Cのx座標は4である。
また、y軸上に点、D(0.8)がある。
四角形ABCDが 平行四辺形となるとき、次の問いに答えよう。
①点Aの座標は?
②直線BDの式は?
③平行四辺形ABCDの面積は?
④原点Oを通り、平行四辺形ABCDの
面積を2等分する直線の式は?
※図は動画内参照
【受験対策】 数学－関数③
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
この動画を見る
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
【受験対策】 数学－規則性②
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
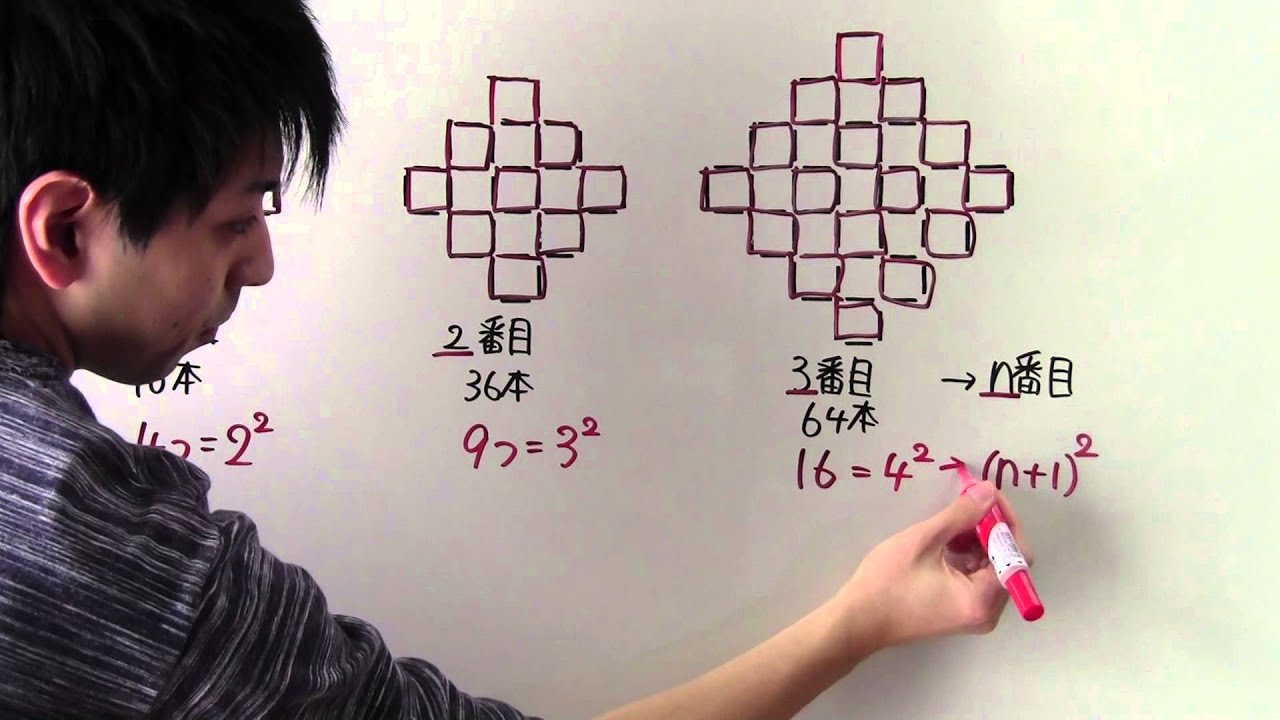
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は、1番目では16本、2番目では36本 3番目では64本である。
①4番目の図形をつくるには何本のマッチ棒が必要?
②n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
この動画を見る
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は、1番目では16本、2番目では36本 3番目では64本である。
①4番目の図形をつくるには何本のマッチ棒が必要?
②n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
【受験対策】 数学－規則性①
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目、3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は1番目では4本、2番目では12本、 3番目では24本である。
①5番目の図形をつくるには何本のマッチ棒が必要?
②14番目の図形をつくるには何本のマッチ棒が必要?
③n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
この動画を見る
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目、3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は1番目では4本、2番目では12本、 3番目では24本である。
①5番目の図形をつくるには何本のマッチ棒が必要?
②14番目の図形をつくるには何本のマッチ棒が必要?
③n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
【受験対策】 数学－関数②
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
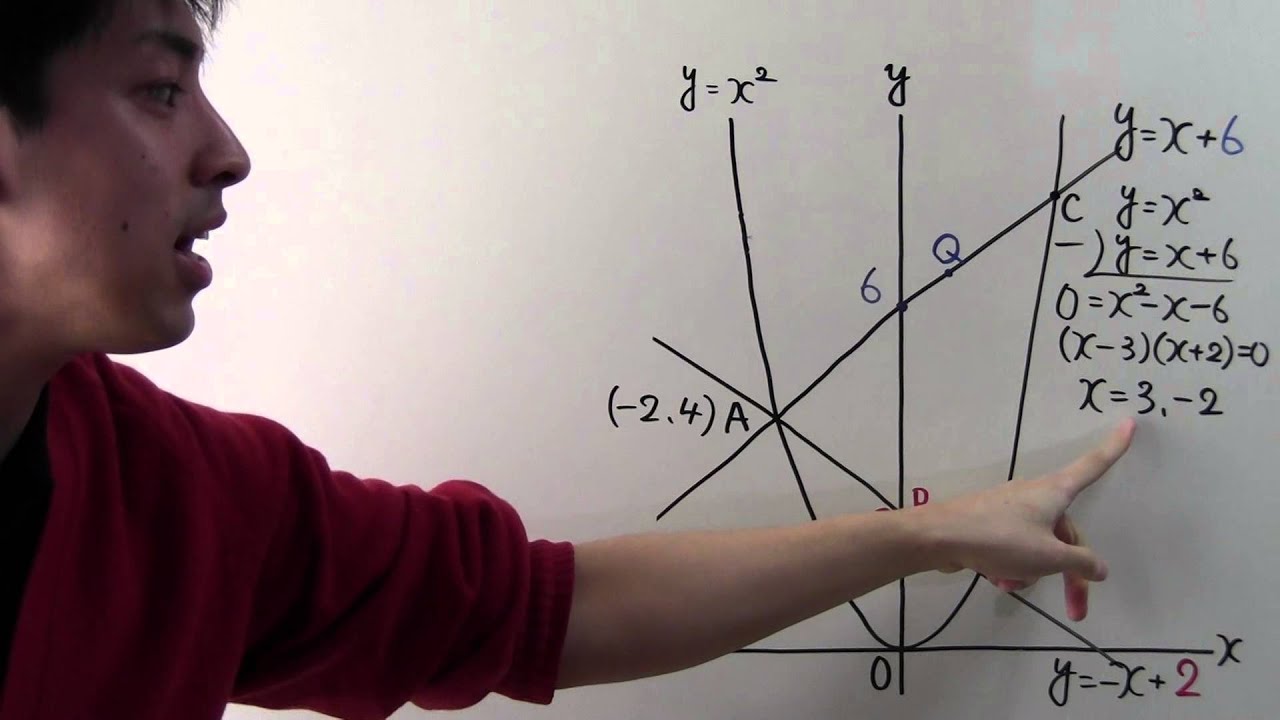
右の図で、曲線は関数$y=x^2$のグラフです。
曲線上の 点A(-2.4)を通り、傾きが-1、1の直線と曲線との交点、をそれぞれB、Cとします。
点P、Qは点Aを同時に出発して、点Pは線分AB上を、点Qは線分AC上を、それぞれ一定の速さで進み、 点Pは点Bに、点Qは点Cに同時に到着しました。
①点Pがy軸上にきたときの点Qの座標は?
②点P、Qが同時に到着した後、点P、Qは線分BC上をそれぞれの速さを変えずに進み、線分BC上の点Rで出会いました。
点Rの座標は?
③△ABRの面積を求めよう。
ただし、座標軸の単位の長さを1cmとします。
※図は動画内参照
この動画を見る
右の図で、曲線は関数$y=x^2$のグラフです。
曲線上の 点A(-2.4)を通り、傾きが-1、1の直線と曲線との交点、をそれぞれB、Cとします。
点P、Qは点Aを同時に出発して、点Pは線分AB上を、点Qは線分AC上を、それぞれ一定の速さで進み、 点Pは点Bに、点Qは点Cに同時に到着しました。
①点Pがy軸上にきたときの点Qの座標は?
②点P、Qが同時に到着した後、点P、Qは線分BC上をそれぞれの速さを変えずに進み、線分BC上の点Rで出会いました。
点Rの座標は?
③△ABRの面積を求めよう。
ただし、座標軸の単位の長さを1cmとします。
※図は動画内参照
【数学】中3-42 二次関数の利用④(一次関数との交点編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図のように、$y=x^2$と$y=x+6$が2点A,Bで交わっている。
①点Aと点Bの座標は？
②△AODの面積は？
③△AOBの面積は？
※図は動画内参照
この動画を見る
◎右の図のように、$y=x^2$と$y=x+6$が2点A,Bで交わっている。
①点Aと点Bの座標は？
②△AODの面積は？
③△AOBの面積は？
※図は動画内参照
【数学】中3-41 二次関数の利用③(一次関数とのコラボ編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図のように、$y=ax^2$のグラフに、2点A,Bがある。
点Aは(-4,8)で、点Bのx座標は2である。
①aの値は？
②点Bの座標は？
③2点A,Bを通る直線の式は？
④△AOBの面積は？
⑤直線A,B場を動く点Pがある。
直線OPが△AOBの面積を2等分するとき、点Pの座標は？
※図は動画内参照
この動画を見る
◎右の図のように、$y=ax^2$のグラフに、2点A,Bがある。
点Aは(-4,8)で、点Bのx座標は2である。
①aの値は？
②点Bの座標は？
③2点A,Bを通る直線の式は？
④△AOBの面積は？
⑤直線A,B場を動く点Pがある。
直線OPが△AOBの面積を2等分するとき、点Pの座標は？
※図は動画内参照
【数学】中3-40 二次関数の利用②(動点編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図のような、AB=4cm、AD=8cmの長方形がある。
点PはAB上を、秒速1cmの速さでAからBまで動き、 点QはAD上を秒速2cmの速さで AからDまで動く。
2点P,Qが同時に,Aを出発してからx秒後の△APQの面積をy$cm^2$とする。
① xとyの関係を式で表すと？
② xの変域は？
③ yの変域は？
④ ①の式をグラフに書くと？
(通る座標を確認してね！)
※図は動画内参照
この動画を見る
◎右の図のような、AB=4cm、AD=8cmの長方形がある。
点PはAB上を、秒速1cmの速さでAからBまで動き、 点QはAD上を秒速2cmの速さで AからDまで動く。
2点P,Qが同時に,Aを出発してからx秒後の△APQの面積をy$cm^2$とする。
① xとyの関係を式で表すと？
② xの変域は？
③ yの変域は？
④ ①の式をグラフに書くと？
(通る座標を確認してね！)
※図は動画内参照
【数学】中3-39 二次関数の利用①(平均の速さ編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎物を落下させるとき、落下しはじめてからx秒間に落下する距離
をymとすると、yはxの2乗に比例する。
落下しはじめてから2秒間で20m落下したとき、次の①～④を解こう!
①xとyの関係を式に表すと?
②落下しはじめてから6秒間 では何m落下する?
③90mのところから落下すると、地上に落ちるまでに何秒かかる?
④落下しはじめてから、2秒後から5秒後までの 平均の速さは?
この動画を見る
◎物を落下させるとき、落下しはじめてからx秒間に落下する距離
をymとすると、yはxの2乗に比例する。
落下しはじめてから2秒間で20m落下したとき、次の①～④を解こう!
①xとyの関係を式に表すと?
②落下しはじめてから6秒間 では何m落下する?
③90mのところから落下すると、地上に落ちるまでに何秒かかる?
④落下しはじめてから、2秒後から5秒後までの 平均の速さは?
【数学】中3-38 二次関数の変化の割合
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$y=ax^2$について、xの値がbからcまで増加したときの変化の割合は①＿＿＿＿で求めよう！
②$y=3x^2$について、xの値が-2から5 まで増加するときの変化の割合は?
③$-\displaystyle \frac{1}{2}x^2$について、xの値が3から7 まで増加するときの変化の割合は?
④$-\displaystyle \frac{1}{3}x^2$について、Xの値がtから $t +1$まで増加するときの変化の割合が -5のとき、tの値はいくつ?
⑤$y=ax^2$について、xの値が-5から3 まで増加するときの変化の割合が、 $y=-3x+6$の変化の割合と等しくなった。
aの値はいくつ?
この動画を見る
$y=ax^2$について、xの値がbからcまで増加したときの変化の割合は①＿＿＿＿で求めよう！
②$y=3x^2$について、xの値が-2から5 まで増加するときの変化の割合は?
③$-\displaystyle \frac{1}{2}x^2$について、xの値が3から7 まで増加するときの変化の割合は?
④$-\displaystyle \frac{1}{3}x^2$について、Xの値がtから $t +1$まで増加するときの変化の割合が -5のとき、tの値はいくつ?
⑤$y=ax^2$について、xの値が-5から3 まで増加するときの変化の割合が、 $y=-3x+6$の変化の割合と等しくなった。
aの値はいくつ?
【数学】中3-37 二次関数の変域
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
変域をだすなら①＿＿＿＿を書こう！
◎yの変域をもとめよう!(②～④) )のとき。
②$y=3x^2(1 \leqq x \leqq 3)$のとき。
③$y=3x^2(-2\leqq x \leqq 1)$のとき。
④$y=-\displaystyle \frac{1}{2}x^2(-1\leqq x \leqq4)$のとき。
⑤$y=ax^2$について、xの変域が$-3 \leqq x \leqq 1$のとき、
yの変域は$0 \leqq y \leqq 18$です。
aの値は？
この動画を見る
変域をだすなら①＿＿＿＿を書こう！
◎yの変域をもとめよう!(②～④) )のとき。
②$y=3x^2(1 \leqq x \leqq 3)$のとき。
③$y=3x^2(-2\leqq x \leqq 1)$のとき。
④$y=-\displaystyle \frac{1}{2}x^2(-1\leqq x \leqq4)$のとき。
⑤$y=ax^2$について、xの変域が$-3 \leqq x \leqq 1$のとき、
yの変域は$0 \leqq y \leqq 18$です。
aの値は？
【数学】中3-36 二次関数のグラフ②
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\boxed{A}～\boxed{D}$の関数からあてはまるものをすべて書こう！
$\boxed{A} y=3x^2$
$\boxed{B} y=-\displaystyle \frac{1}{5}x^2$
$\boxed{C} y=-x^2$
$\boxed{D} y=\displaystyle \frac{2}{3}x^2$
①グラフが下に開いているのは？
②グラフの開き方が一番大きいのは？
③グラフが$y=x^2$とx軸を対象の軸として線対称になっているのはどれ？
④$x=0$のとき、yが最小になるのは？
⑤$x＜0$の範囲で、xの値が増加するとyの値が減少するのは？
⑥$\boxed{ア}～\boxed{エ}$の中で、$\boxed{C}$と$\boxed{D}$のグラフはどれ？
$\boxed{C}$→ 、$\boxed{D}$→
※グラフは動画内参照
この動画を見る
$\boxed{A}～\boxed{D}$の関数からあてはまるものをすべて書こう！
$\boxed{A} y=3x^2$
$\boxed{B} y=-\displaystyle \frac{1}{5}x^2$
$\boxed{C} y=-x^2$
$\boxed{D} y=\displaystyle \frac{2}{3}x^2$
①グラフが下に開いているのは？
②グラフの開き方が一番大きいのは？
③グラフが$y=x^2$とx軸を対象の軸として線対称になっているのはどれ？
④$x=0$のとき、yが最小になるのは？
⑤$x＜0$の範囲で、xの値が増加するとyの値が減少するのは？
⑥$\boxed{ア}～\boxed{エ}$の中で、$\boxed{C}$と$\boxed{D}$のグラフはどれ？
$\boxed{C}$→ 、$\boxed{D}$→
※グラフは動画内参照
【数学】中3-35 二次関数のグラフ①
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$y=ax^2$のグラフは、 必ず①＿＿＿＿を通る。
そしてaが＿＿＿＿だと上カーブ!
aが③＿＿＿＿だと下カーブ!!
◎グラフを書こう!
④$y=\displaystyle \frac{1}{4}x^2$
⑤$y=-x^2$
⑥グラフの式をもとめよう。
※グラフは動画内参照
この動画を見る
$y=ax^2$のグラフは、 必ず①＿＿＿＿を通る。
そしてaが＿＿＿＿だと上カーブ!
aが③＿＿＿＿だと下カーブ!!
◎グラフを書こう!
④$y=\displaystyle \frac{1}{4}x^2$
⑤$y=-x^2$
⑥グラフの式をもとめよう。
※グラフは動画内参照