 円
円
 円
円
【数学】中高一貫校問題集2幾何97:円:円周角の定理:弧の長さ
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
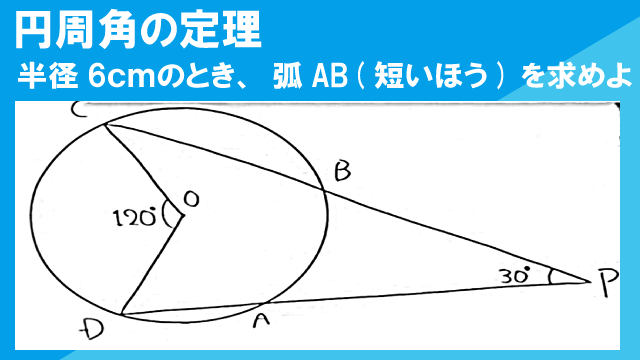
図のように、半径が6cmの円Oの周上に、4点A,B,C,Dがあり、DAとCBの交点をPとする。∠CPD=30°、∠COD=120°のとき、弧AB(点Cを含まない方)の長さを求めなさい。
この動画を見る
図のように、半径が6cmの円Oの周上に、4点A,B,C,Dがあり、DAとCBの交点をPとする。∠CPD=30°、∠COD=120°のとき、弧AB(点Cを含まない方)の長さを求めなさい。
【数学】中高一貫校問題集2幾何96:円:円周角の定理:ブーメラン型
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
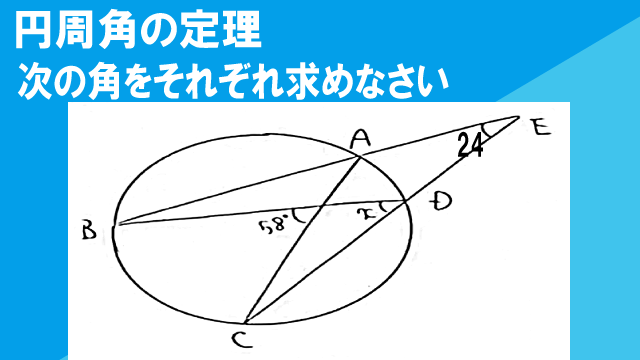
図において、∠xの大きさを求めなさい。
この動画を見る
図において、∠xの大きさを求めなさい。
【数学】中高一貫校問題集2幾何95:円:円周角の定理:弧の比と角の比、12等分するとき
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
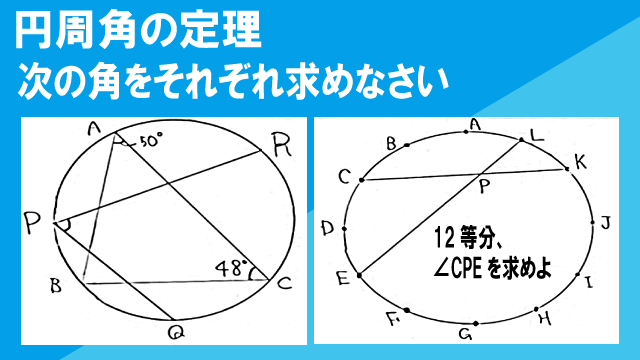
(1)図1で、点Qは弧BCを2等分する点、点Rは弧CAを2等分する点である。∠CAB=50°、∠BCA=48°であるとき、∠RPQの大きさを求めなさい。
(2)図2で、点A~Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めなさい。
この動画を見る
(1)図1で、点Qは弧BCを2等分する点、点Rは弧CAを2等分する点である。∠CAB=50°、∠BCA=48°であるとき、∠RPQの大きさを求めなさい。
(2)図2で、点A~Lは、円周を12等分する点である。CKとELの交点をPとするとき、∠CPEの大きさを求めなさい。
【数学】中高一貫校問題集2幾何94:円:円周角の定理:ブーメラン型、直径を通るとき
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
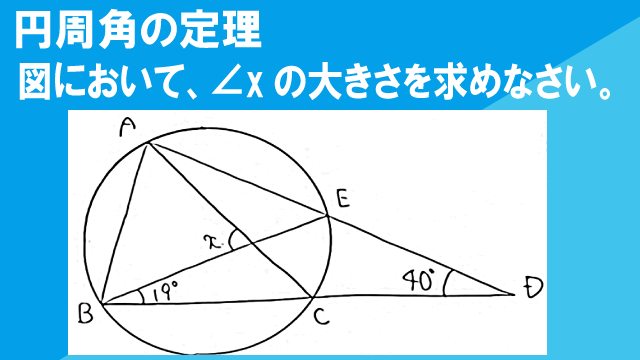
図において、∠xの大きさを求めなさい。点Oは円の中心である。
この動画を見る
図において、∠xの大きさを求めなさい。点Oは円の中心である。
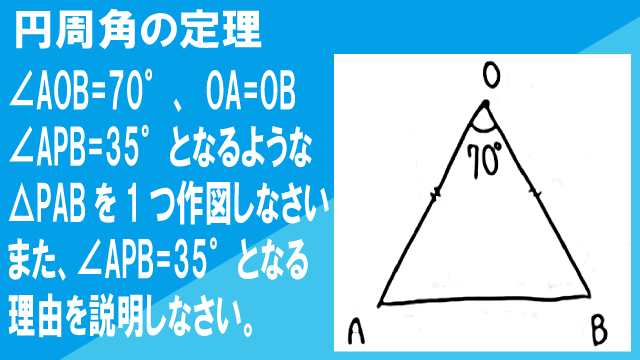
【数学】中高一貫校問題集2幾何100:円:円周角の定理:作図
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図の△OAは、∠AOB=70°、OA=OBの二等辺三角形である。∠APB=35°となるような△PABを1つ作図しなさい。また、∠APB=35°となる理由を説明しなさい。
この動画を見る
図の△OAは、∠AOB=70°、OA=OBの二等辺三角形である。∠APB=35°となるような△PABを1つ作図しなさい。また、∠APB=35°となる理由を説明しなさい。
中学入試 円 開智中
高等学校入学試験予想問題:三重県公立高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
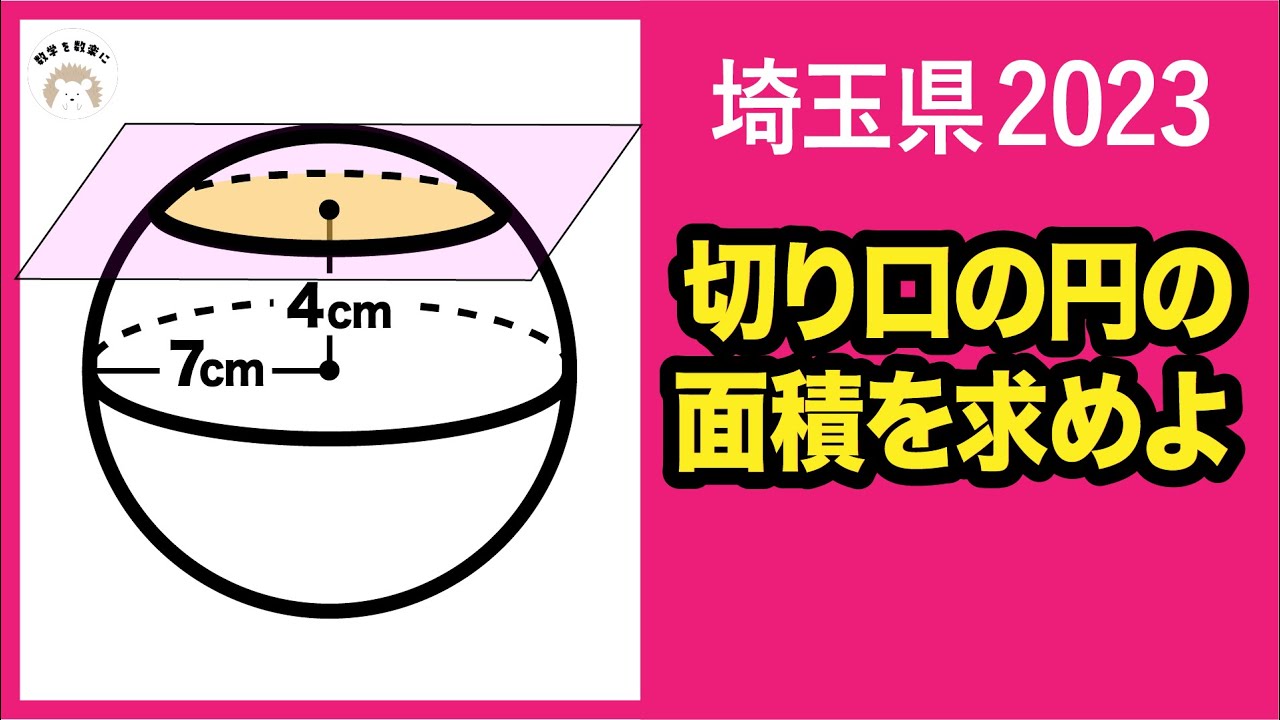
2023高校入試数学解説83問目 球の切り口の面積は? 埼玉県
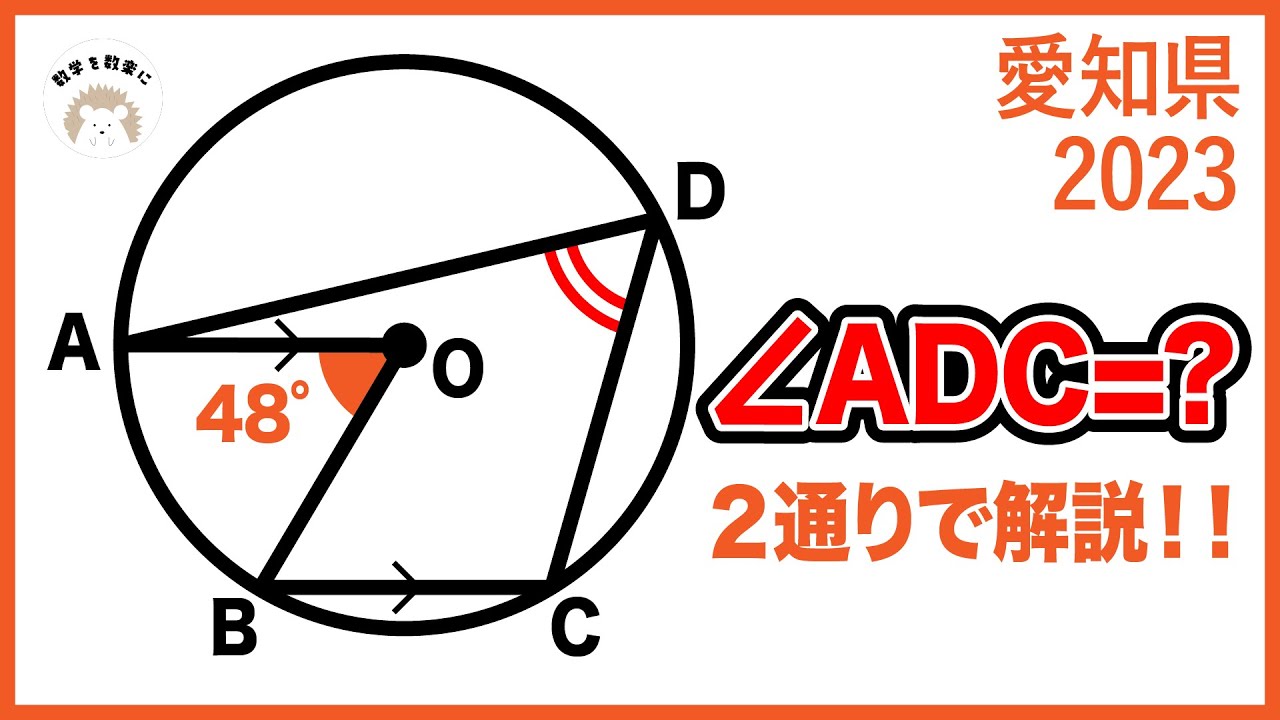
2023高校入試数学解説77問目 円周角 愛知県
【たったこれだけの条件で…!】図形:広島大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
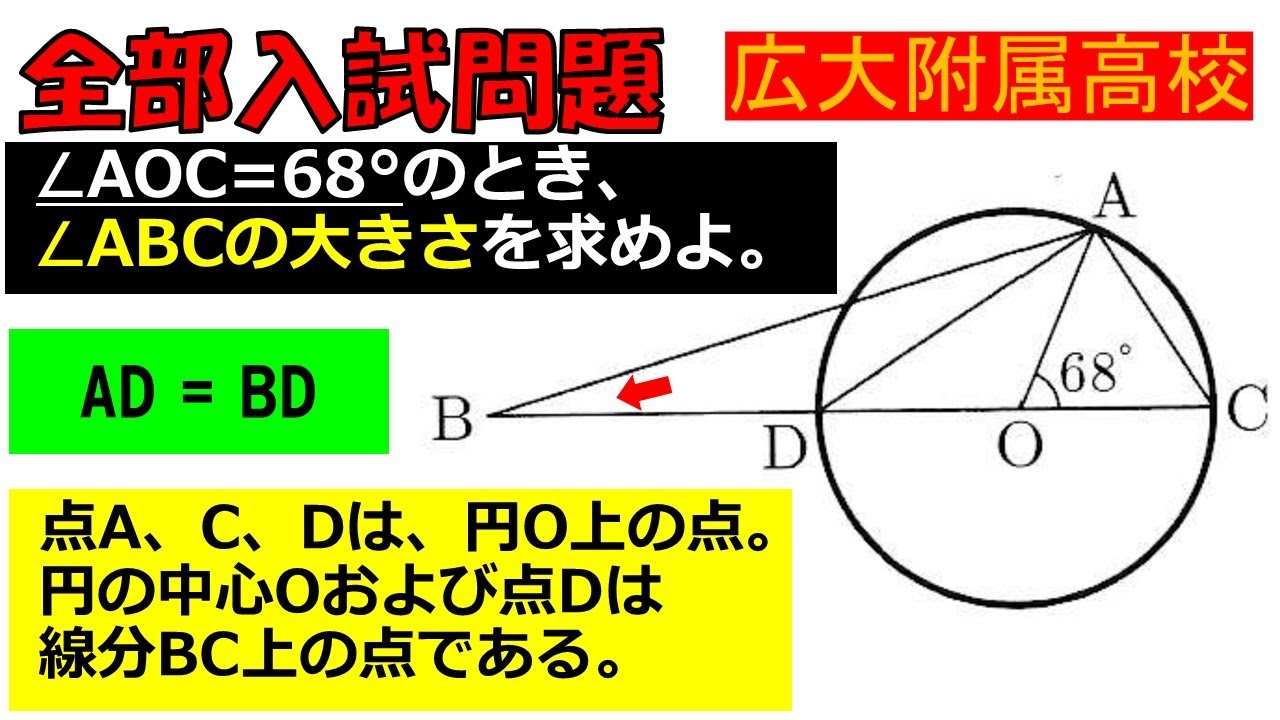
点A,C,Dは円O上の点である.
円の中心Oおよび点Dは線分BC上の点である.
$ \angle AOC=68°$のとき,$ \angle ABC $の大きさを求めよ.
広大付属高校過去問
この動画を見る
点A,C,Dは円O上の点である.
円の中心Oおよび点Dは線分BC上の点である.
$ \angle AOC=68°$のとき,$ \angle ABC $の大きさを求めよ.
広大付属高校過去問
2023高校入試数学解説65問目 気付けば一瞬!!座標平面上の円 城北高校 (再)
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
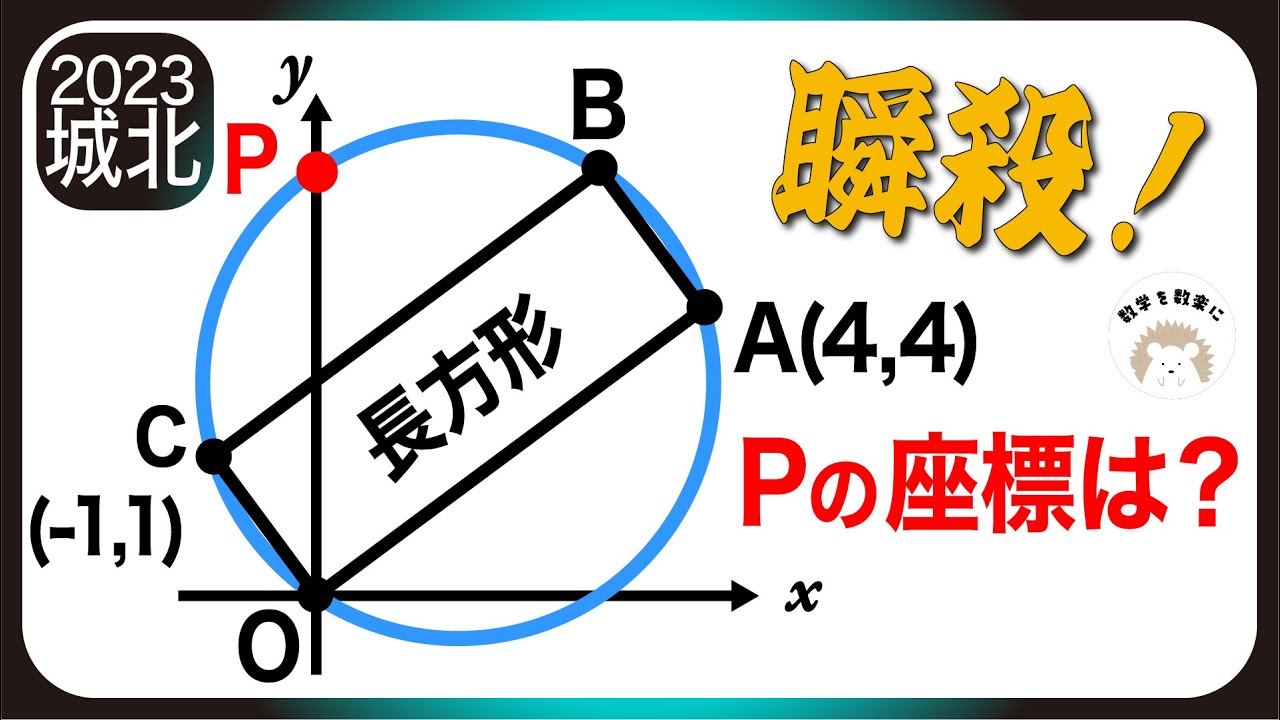
四角形OCBAは長方形
Pの座標は?
*図は動画内参照
2023城北学園高等学校
この動画を見る
四角形OCBAは長方形
Pの座標は?
*図は動画内参照
2023城北学園高等学校
高等学校入学試験予想問題:明治学院高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#空間図形#1次関数#2次関数#円#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
高等学校入学試験予想問題:近畿大学附属高等学校~全部入試問題

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \dfrac{4x-y}{9}-\dfrac{5x-4y}{12}$を計算せよ.
(2)$ xy-3y-3x+9 $を因数分解せよ.
(3)
$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-y=1 \\
2ax+by=16
\end{array}
\right.
\end{eqnarray}$
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax+2y=8 \\
-3x+2y=3
\end{array}
\right.
\end{eqnarray}$
が同じ解をもつとき,$ a,b $の値を求めよ.
$ \boxed{2}$
図のように,関数$ y=x^2 $のグラフと直線$ y=-2x+8 $との交点を$ A,B,$直線$AB $の中点を$M$とするとき,次の問いに答えよ.
ただし,点$A$のx座標は負とする.
(1)点$A$の座標を求めよ.
(2)直線$OM$の式を求めよ.
(3)$ \triangle OCM $をx軸のまわりに1回転させてできる立体の体積を求めよ.
$ \boxed{3}$
図のように,点$O$を中心とし,線分$AB$を直径とする半径6の円があり,点$C$は線分$OB$の中点である,2点$D,E$は直径$AB$に対して同じ側の円周上にあり,$AB$と$CD$は直角,$AB$と$OE$は直角となっている.
また,線分$AD$と線分$OE$の交点を点$F$とする.
このとき,次の問いに答えよ.
(1)$CD$の長さを求めよ.
(2)$ \triangle AEF$の面積を求めよ.
(3)$ AF:AD$の比を求めよ.また,$\triangle DEF $の面積を求めよ.
2023高校入試解説21問目 2通りで解説!!座標平面上の円 久留米大附設
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
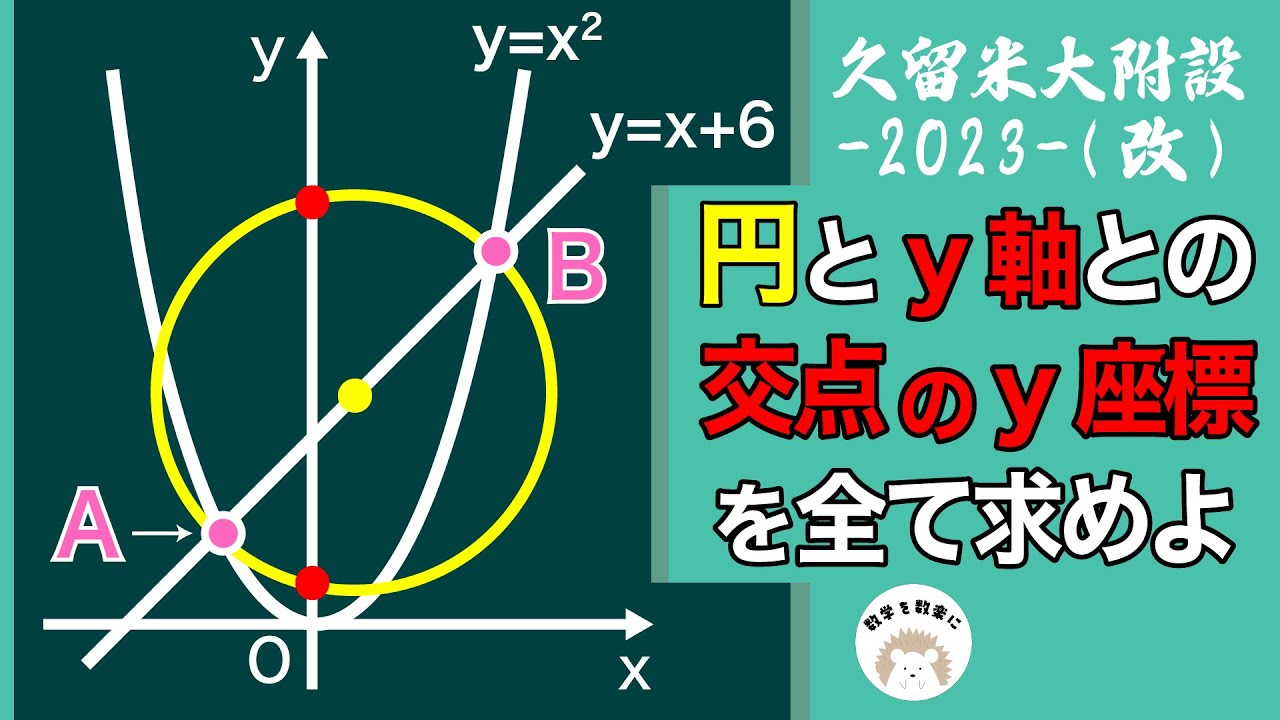
円とy軸との交点のy座標を全て求めよ
*図は動画内参照
2023久留米大学附設高等学校(改)
この動画を見る
円とy軸との交点のy座標を全て求めよ
*図は動画内参照
2023久留米大学附設高等学校(改)
難関高校受験者必見!!公式まとめます。図形

単元:
#数学(中学生)#中1数学#中2数学#中3数学#空間図形#平行と合同#相似な図形#円#三平方の定理#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
難関高校受験者必見!!公式まとめます。図形
この動画を見る
難関高校受験者必見!!公式まとめます。図形
【解法はいろいろあるから!】図形:新潟県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#角度と面積#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
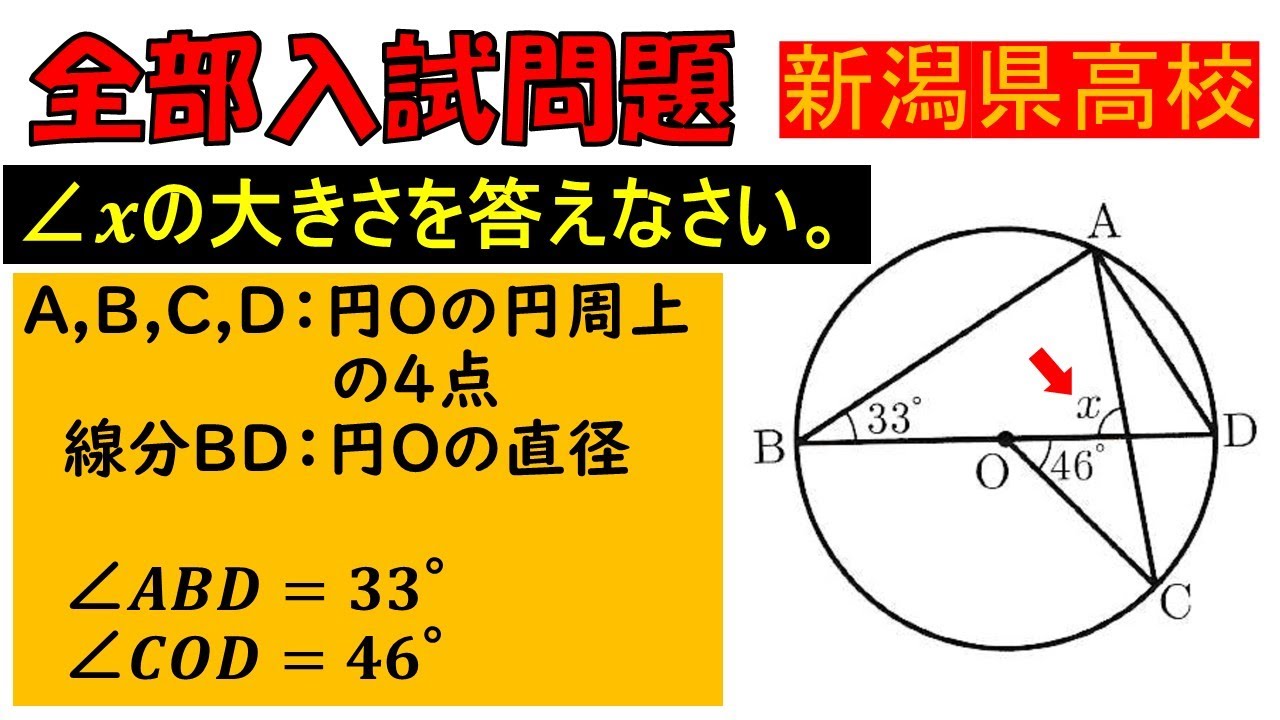
$A,B,C,D$は円$O$の円周上の4点であり,線分$BD$は円$O$の直径である.
$ \angle ABD=33°,\angle COD=46°$である.
$ \angle x$の大きさを答えなさい.
新潟県高校過去問
この動画を見る
$A,B,C,D$は円$O$の円周上の4点であり,線分$BD$は円$O$の直径である.
$ \angle ABD=33°,\angle COD=46°$である.
$ \angle x$の大きさを答えなさい.
新潟県高校過去問
難関高校受験する生徒へ 塾で習う公式まとめてみた。図形編はまた、いつかやります!!

単元:
#数学(中学生)#中1数学#中2数学#中3数学#空間図形#平行と合同#相似な図形#円#三平方の定理#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
難関高校受験する生徒へ 塾で習う公式まとめてみた。図形編はまた、いつかやります!!
この動画を見る
難関高校受験する生徒へ 塾で習う公式まとめてみた。図形編はまた、いつかやります!!
中学入試でも二つの円!!開成中
半円と正方形
【得意分野にしよう!】図形:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
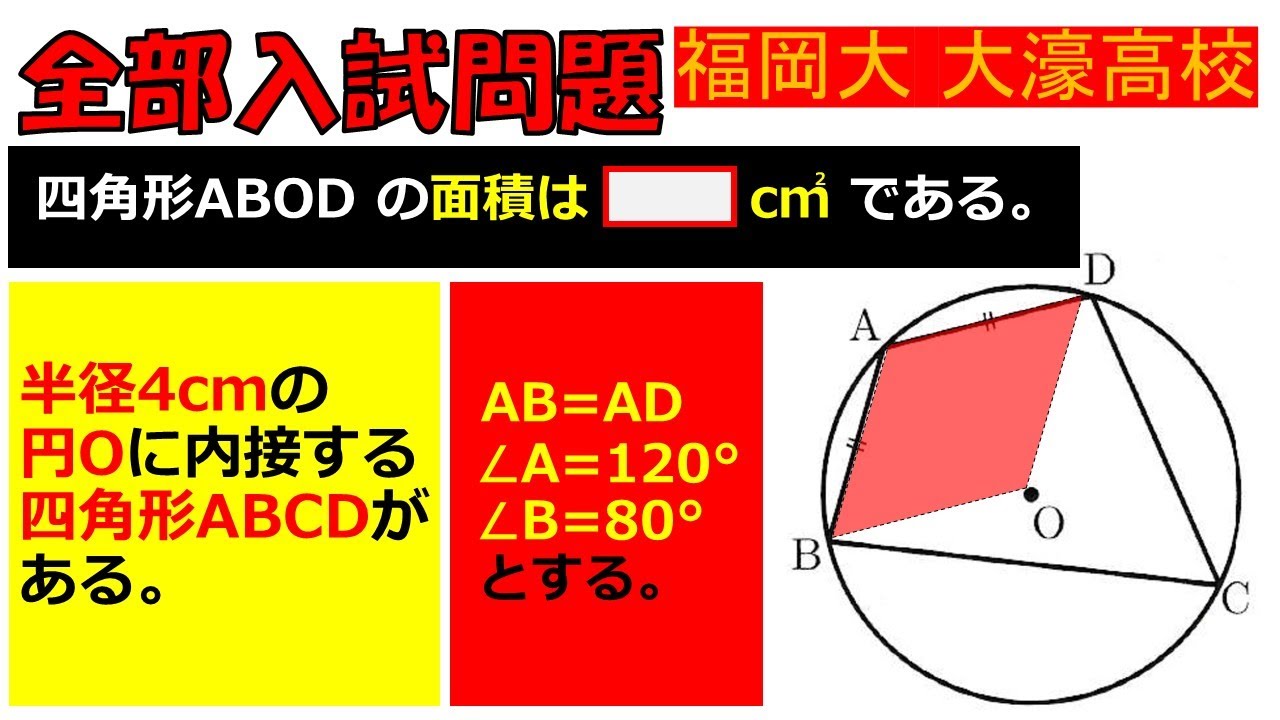
半径4cmの円$O$に内接する四角形$ABCD$がある.
$AB=AD,\angle A=120°,\angle B=80°$とする.
四角形$ABCD$の面積は$\Box cm^2$である.
福岡大学附属大濠高等学校過去問
この動画を見る
半径4cmの円$O$に内接する四角形$ABCD$がある.
$AB=AD,\angle A=120°,\angle B=80°$とする.
四角形$ABCD$の面積は$\Box cm^2$である.
福岡大学附属大濠高等学校過去問
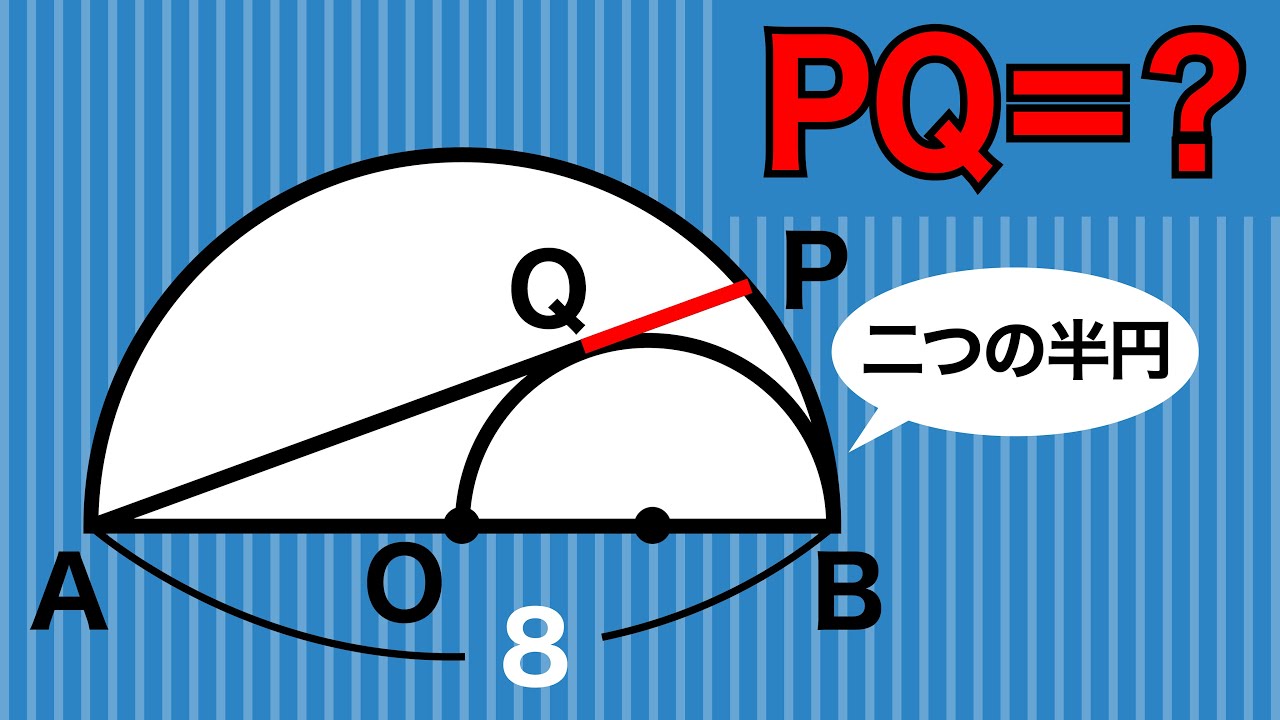
2つの半円
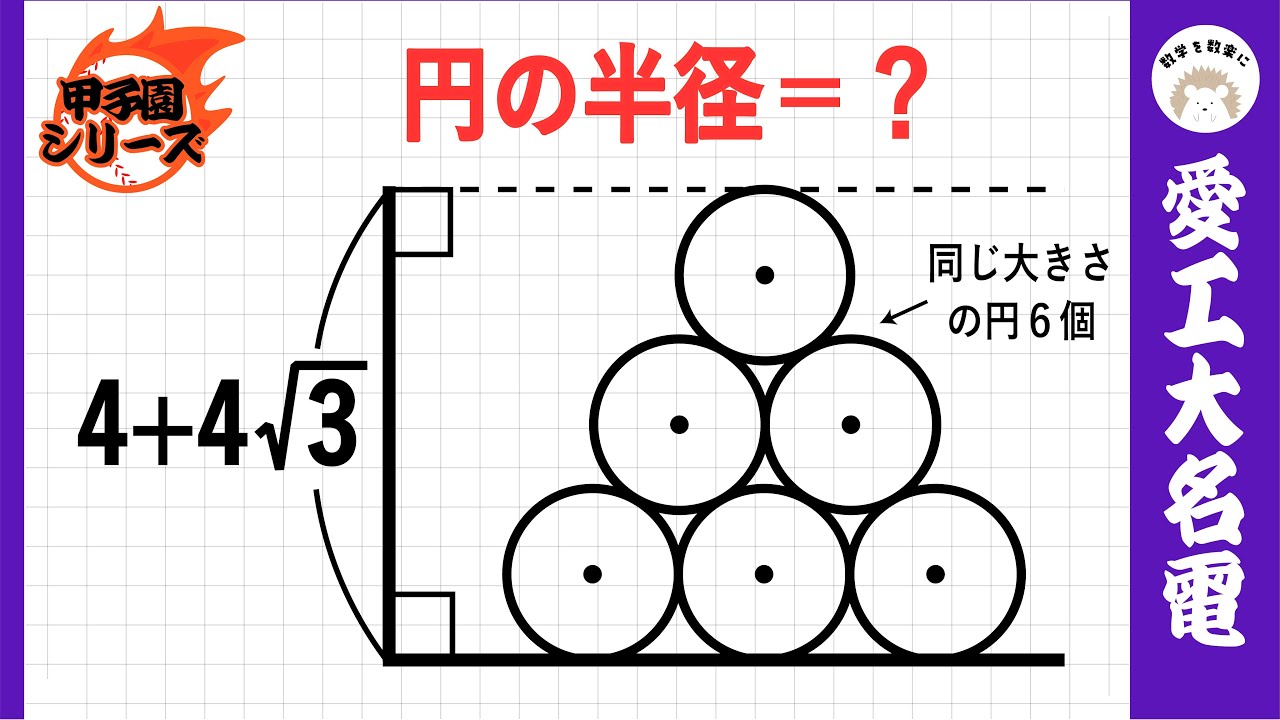
複数個の円 愛工大名電
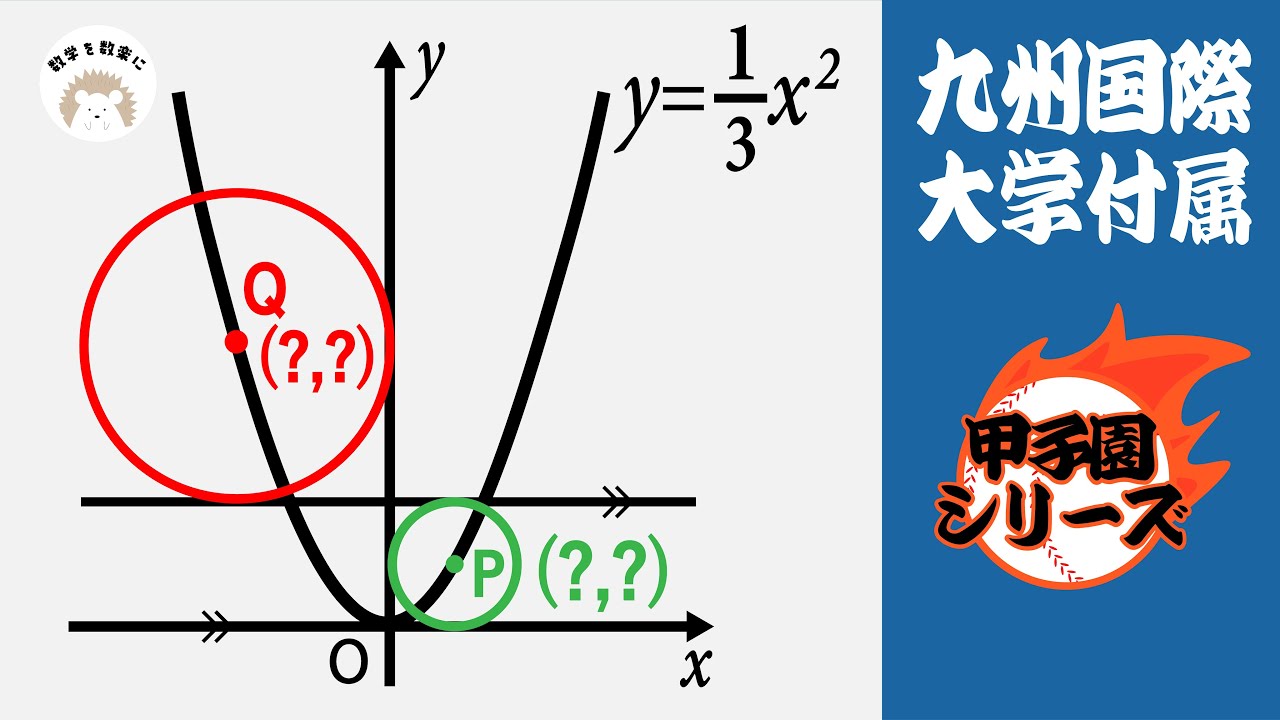
放物線と2つの円 中心の座標は? 九州国際大付属
単元:
#数学(中学生)#中3数学#2次方程式#円#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
点P、Qの座標は?
*図は動画内参照
九州国際大学付属高等学校
この動画を見る
点P、Qの座標は?
*図は動画内参照
九州国際大学付属高等学校
円 角の和 大阪桐蔭
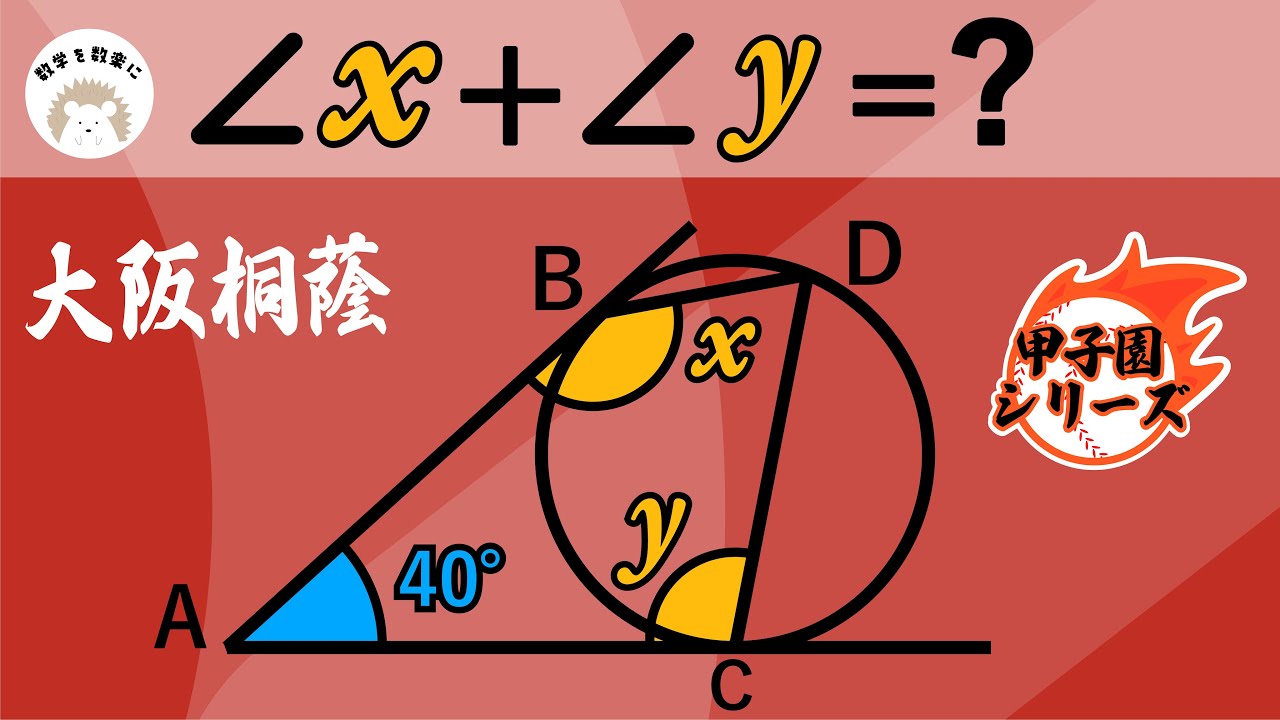
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x +\angle y = ?$
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
$\angle x +\angle y = ?$
*図は動画内参照
大阪桐蔭高等学校
中学生の解き方 高校生の解き方 日本文理
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
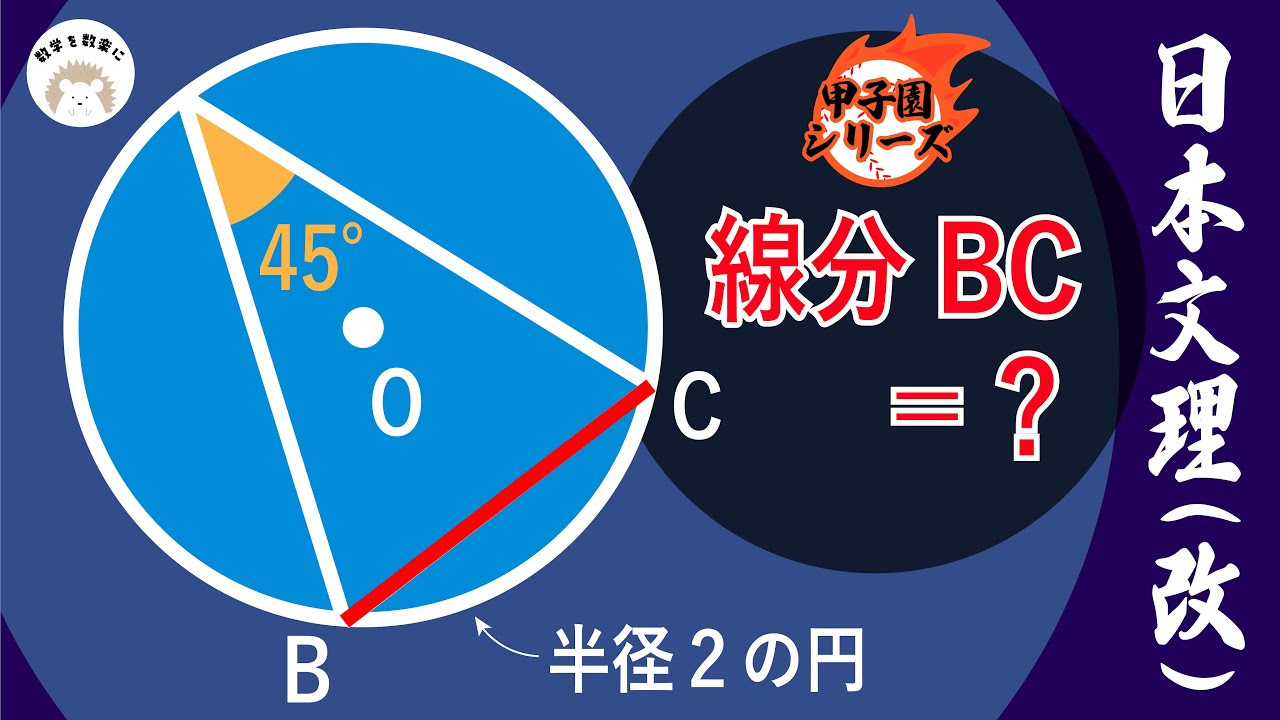
円の半径=2
線分BC=?
*図は動画内参照
日本文理高等学校(改)
この動画を見る
円の半径=2
線分BC=?
*図は動画内参照
日本文理高等学校(改)
斜線部の面積を求めよ 樹徳高校

斜線部の面積=❓ 日大三島
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
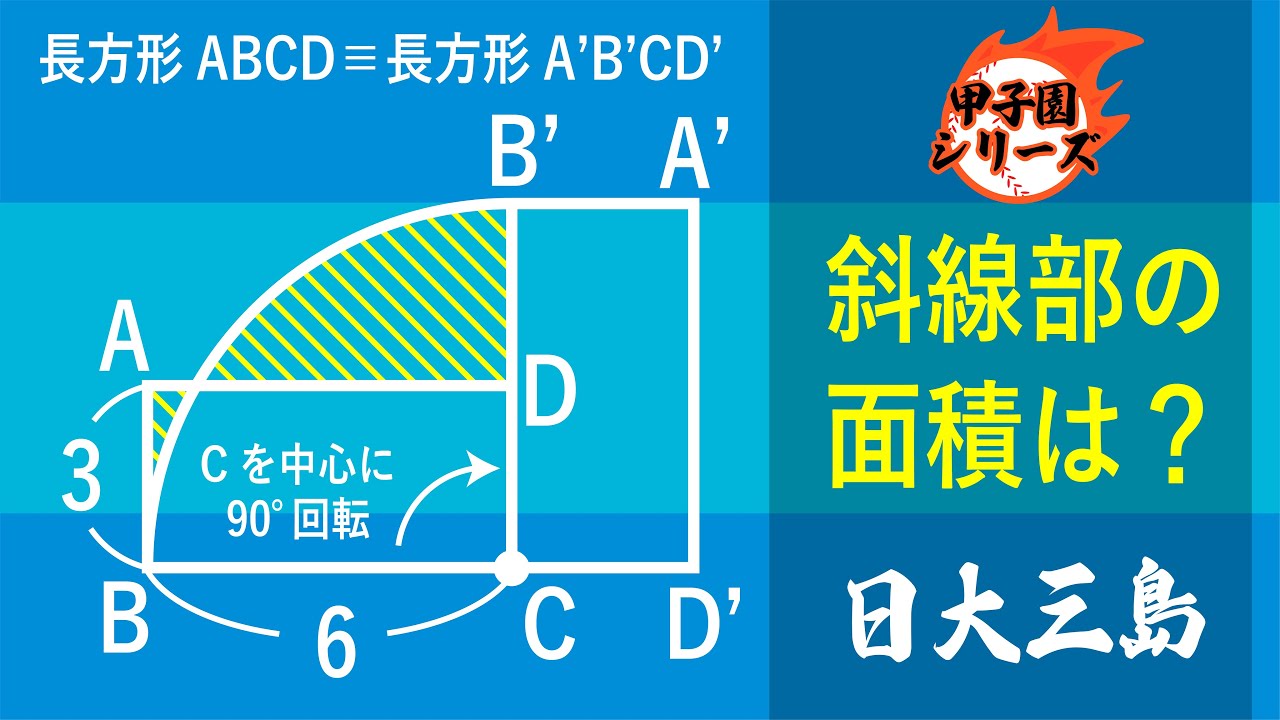
長方形ABCD≡長方形A'B'C'D'
斜線部の面積は?
*図は動画内参照
日本大学三島高等学校
この動画を見る
長方形ABCD≡長方形A'B'C'D'
斜線部の面積は?
*図は動画内参照
日本大学三島高等学校
小学生も解ける!? 円の面積
数学の基礎から学ぶ15秒の七夕ダ~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中1数学#中3数学#空間図形#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
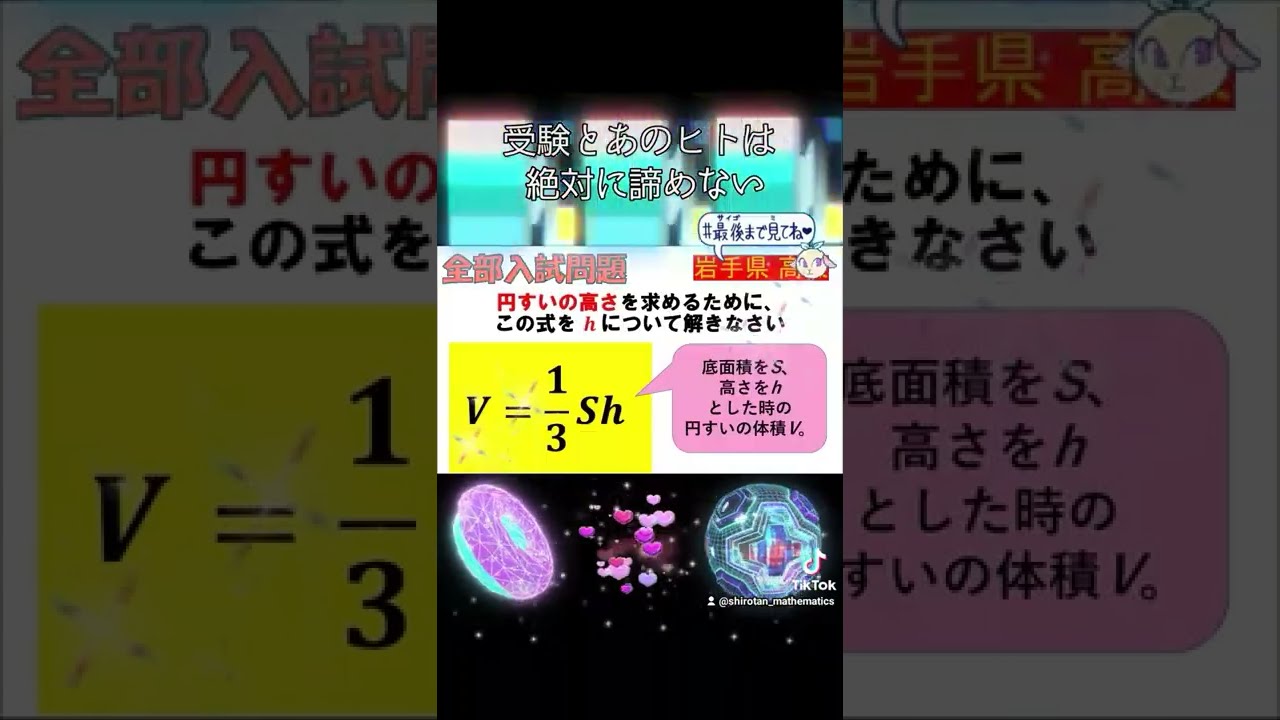
円錐の体積$V$は$V=\dfrac{1}{3}SH$である.
$H$のついて解きなさい.($S$は底面積であり,$H$は高さ)
この動画を見る
円錐の体積$V$は$V=\dfrac{1}{3}SH$である.
$H$のついて解きなさい.($S$は底面積であり,$H$は高さ)
和が分かればいい 筑波大学附属
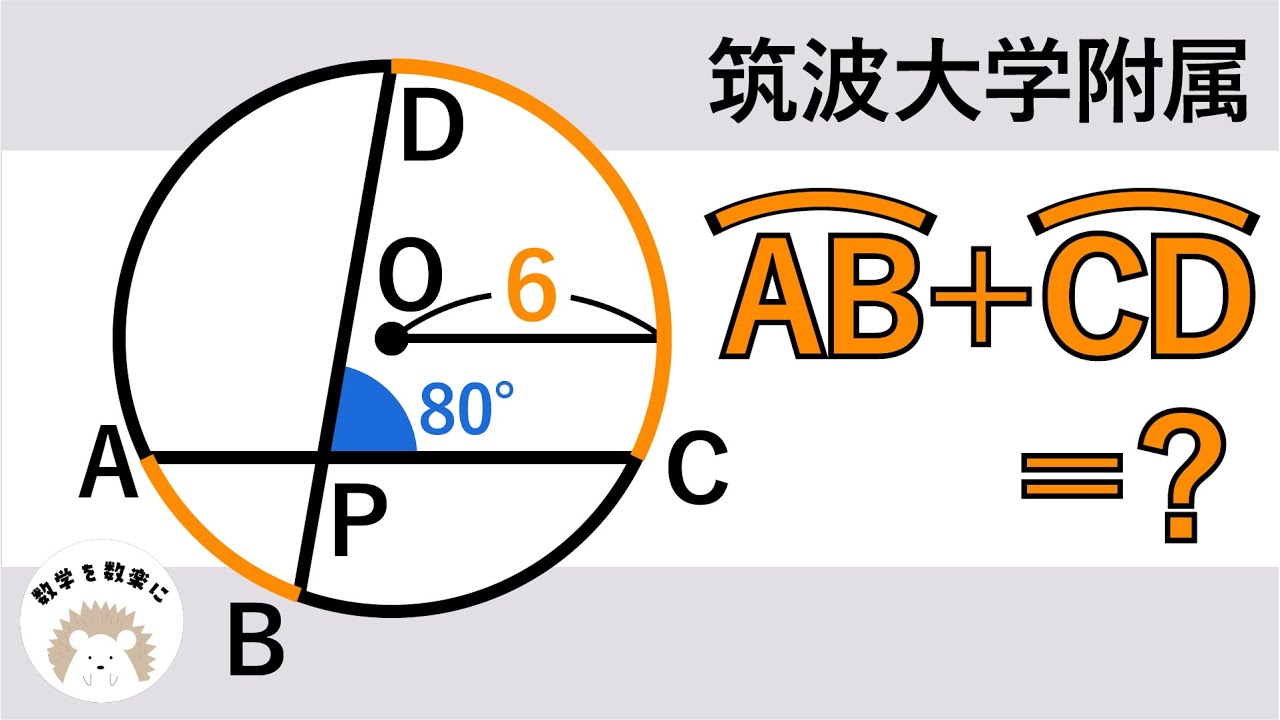
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AB} + \stackrel{\huge\frown}{CD} = ?$
*図は動画内参照
筑波大学附属高等学校
この動画を見る
$\stackrel{\huge\frown}{AB} + \stackrel{\huge\frown}{CD} = ?$
*図は動画内参照
筑波大学附属高等学校
