円
円
角度を求める（2006国立高校）
単元：
#数学(中学生)#中２数学#中３数学#円#三角形と四角形#高校入試過去問(数学)#東京都立国立高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
動画内の図を参照し、？の角度を求めよ。
出典：2006年国立高校
この動画を見る
動画内の図を参照し、？の角度を求めよ。
出典：2006年国立高校
角度を求める！（都立西2005 2006）
円周角を一発で！！（中3数学）
補助せえん（城北2012改題）
三角形と内接円（高校入試数学 数I）
ブーメランの角と円周角（高校入試数学）
直角三角形の性質（高校入試数学）
単元：
#数学(中学生)#中２数学#中３数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#三角形と四角形#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
直角三角形の性質についての説明動画です
この動画を見る
直角三角形の性質についての説明動画です
円に内接する四角形（数A 高校入試数学）
単元：
#数学(中学生)#中３数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係
指導講師：
数学を数楽に
問題文全文(内容文)：
円に内接する四角形の性質について説明動画です
この動画を見る
円に内接する四角形の性質について説明動画です
中学数学 作図４ 共通外接線
【高校受験対策】数学-死守38
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#連立方程式#２次方程式#1次関数#確率#2次関数#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
福田の一夜漬け数学〜図形と方程式〜円の方程式(3)直線と円の位置関係、高校2年生
単元：
#数Ⅱ#円#図形と方程式#円と方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 直線$mx-y-(3m-1)=0$ と円$x^2+y^2=2$ の位置関係を調べよ。
この動画を見る
${\Large\boxed{1}}$ 直線$mx-y-(3m-1)=0$ と円$x^2+y^2=2$ の位置関係を調べよ。
質問に対する返答動画です。円の性質、三平方の定理、計算の工夫、
単元：
#数学(中学生)#中３数学#円#三平方の定理
指導講師：
鈴木貫太郎
問題文全文(内容文)：
右の図のように、半径2の外接する2円A,Bが半径5の円Oに内接している。
2円A,Bに外接する円Oに内接する円Cの半径を求めよ。
＊図は動画内参照
この動画を見る
右の図のように、半径2の外接する2円A,Bが半径5の円Oに内接している。
2円A,Bに外接する円Oに内接する円Cの半径を求めよ。
＊図は動画内参照
ご質問に対する返答動画です。円の面積はなぜπｒ＾２
【高校受験対策】数学-死守29
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#２次方程式#1次関数#2次関数#円#立体図形#立体切断#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$16a \div (- 8)$を計算しなさい。
②$-12 + 2\times (- 5)$を計算しなさい。
③$\sqrt{50} - 2\sqrt{2}$を計算しなさい。
④$18ab \div \dfrac{3}{8}a \times b$を計算しなさい。
⑤$x = sqrt3 - 3$のとき、$x ^ 2 + 6x$の値を求めなさい。
⑥2次方程式$x ^ 2 + 3x = 8x - 2$を解きなさい。
⑦$\sqrt7 = 2.646$として、$\sqrt{0.07} $の値を求めなさい。
⑧右の図1は、立方体の展開図である。 この展開図を組み立てて作られる立方体について、
辺$AB$と垂直な面をア~カのなかからすべて選び、符号で書きなさい。
⑨その値が正の値をとらない関数を、次のア~エから1つ選び、符号で書きなさい。
ア→$y= -\dfrac{x}{2}$
イ→$y = -\dfrac{2}{x}$
ウ→$y = -2x + 3$
エ→$y = - 2x ^ 2$
⑩右の図2は、円錐の展開図である。
側面になるおうぎ形の半径が8cm、 底面になる円の半径が3cmのとき、
おうぎ形の面積を求めなさい。 ただし、円周率は$\pi$とする。
図は動画内参照
この動画を見る
①$16a \div (- 8)$を計算しなさい。
②$-12 + 2\times (- 5)$を計算しなさい。
③$\sqrt{50} - 2\sqrt{2}$を計算しなさい。
④$18ab \div \dfrac{3}{8}a \times b$を計算しなさい。
⑤$x = sqrt3 - 3$のとき、$x ^ 2 + 6x$の値を求めなさい。
⑥2次方程式$x ^ 2 + 3x = 8x - 2$を解きなさい。
⑦$\sqrt7 = 2.646$として、$\sqrt{0.07} $の値を求めなさい。
⑧右の図1は、立方体の展開図である。 この展開図を組み立てて作られる立方体について、
辺$AB$と垂直な面をア~カのなかからすべて選び、符号で書きなさい。
⑨その値が正の値をとらない関数を、次のア~エから1つ選び、符号で書きなさい。
ア→$y= -\dfrac{x}{2}$
イ→$y = -\dfrac{2}{x}$
ウ→$y = -2x + 3$
エ→$y = - 2x ^ 2$
⑩右の図2は、円錐の展開図である。
側面になるおうぎ形の半径が8cm、 底面になる円の半径が3cmのとき、
おうぎ形の面積を求めなさい。 ただし、円周率は$\pi$とする。
図は動画内参照
【高校受験対策】数学-図形18
単元：
#数学(中学生)#中１数学#中２数学#中３数学#円#平面図形#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
この動画を見る
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
【高校受験対策】数学-死守27
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#平方根#２次方程式#比例・反比例#空間図形#円#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$x-6x$を計算しなさい。
②$\sqrt{28)}- \sqrt{7}$を計算しなさい。
③$x = sqrt2 + 3$のとき、$x ^ 2 - 6x + 9$の値を求めなさい。
④2次方程式$x ^ 2 - 2x - 7 = 0$を解きなさい。
⑤次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=4 \\
3x+2y=19
\end{array}
\right.
\end{eqnarray}$
⑥$y$は$x$に反比例し、$x = - 4a$のとき、$y = 3$です。
$x = 2$のときの$y$の値を求めなさい。
⑦中学生12人が、あるゲームを行いました。
左下の資料1は、そのゲームの得点を示したものです。
この資料の中央値(メジアン)と分布の範囲をそれぞれ求めなさい。
⑧半径が8cm、弧の長さが4匹cmのおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨ある2けたの自然数は、十の位の数と一の位の数の和が10で、
十の位の数と一の位の数の積が21です。
この2けたの自然数として考えられる数をすべて求めなさい。
⑩右の図のような三角柱$ABC-DEF$があります。
点$G$は辺$AD$の中点です。
三角柱$ABC-DEF$の体積は三角錐$G-DEF$の体積の何倍ですか。
図は動画内参照
この動画を見る
①$x-6x$を計算しなさい。
②$\sqrt{28)}- \sqrt{7}$を計算しなさい。
③$x = sqrt2 + 3$のとき、$x ^ 2 - 6x + 9$の値を求めなさい。
④2次方程式$x ^ 2 - 2x - 7 = 0$を解きなさい。
⑤次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=4 \\
3x+2y=19
\end{array}
\right.
\end{eqnarray}$
⑥$y$は$x$に反比例し、$x = - 4a$のとき、$y = 3$です。
$x = 2$のときの$y$の値を求めなさい。
⑦中学生12人が、あるゲームを行いました。
左下の資料1は、そのゲームの得点を示したものです。
この資料の中央値(メジアン)と分布の範囲をそれぞれ求めなさい。
⑧半径が8cm、弧の長さが4匹cmのおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨ある2けたの自然数は、十の位の数と一の位の数の和が10で、
十の位の数と一の位の数の積が21です。
この2けたの自然数として考えられる数をすべて求めなさい。
⑩右の図のような三角柱$ABC-DEF$があります。
点$G$は辺$AD$の中点です。
三角柱$ABC-DEF$の体積は三角錐$G-DEF$の体積の何倍ですか。
図は動画内参照
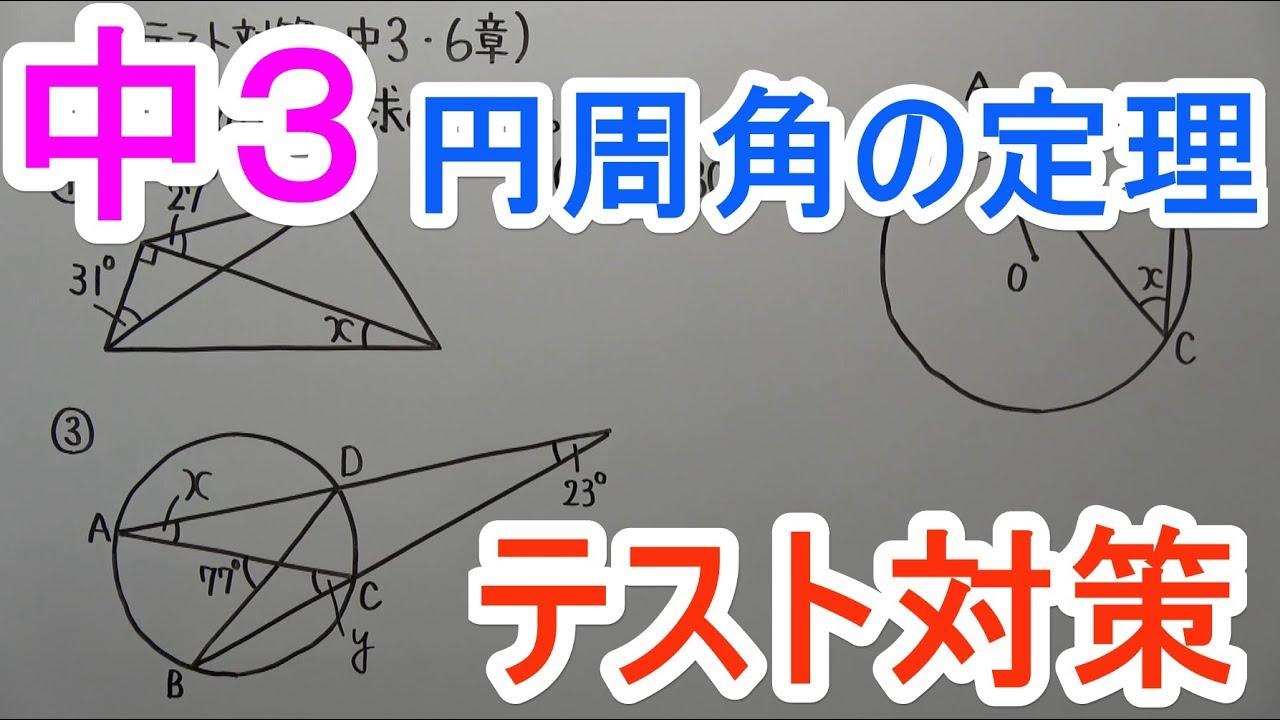
【テスト対策 中3】6章-5
単元：
#数学(中学生)#中２数学#中３数学#円#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\angle x,\angle y$の大きさを求めなさい。
図①～③は動画内参照
この動画を見る
$\angle x,\angle y$の大きさを求めなさい。
図①～③は動画内参照
【テスト対策 中3】6章-4
単元：
#数学(中学生)#中３数学#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①下の図1は線分$AF$を直径とする半円$O$で、
点$B~E$は弧$AF$を5等分する点である。
このとき、$\angle x$の大きさを求めなさい。
②下の図2で、点$A~F$は円周上の6等分点である。
このとき、$\angle x$の大きさを求めなさい。
図は動画内参照
この動画を見る
①下の図1は線分$AF$を直径とする半円$O$で、
点$B~E$は弧$AF$を5等分する点である。
このとき、$\angle x$の大きさを求めなさい。
②下の図2で、点$A~F$は円周上の6等分点である。
このとき、$\angle x$の大きさを求めなさい。
図は動画内参照
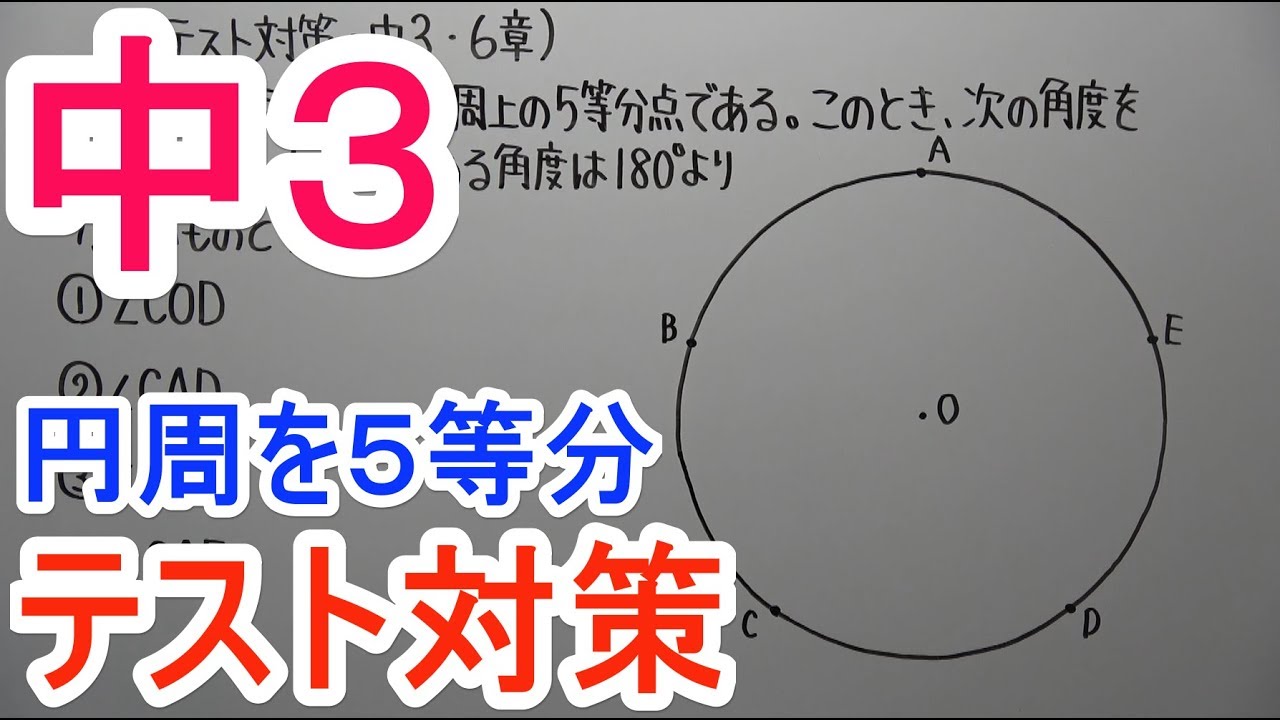
【テスト対策 中3】6章-3
単元：
#数学(中学生)#中３数学#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図で、点$A~E$は円周上の5等分点である。
このとき、次の角度を求めなさい。
ただし、求める角度は$180°$より小さいものとする。
①$\angle COD$
②$\angle CAD$
③$\angle BOD$
④$\angle CAE$
図は動画内参照
この動画を見る
◎右の図で、点$A~E$は円周上の5等分点である。
このとき、次の角度を求めなさい。
ただし、求める角度は$180°$より小さいものとする。
①$\angle COD$
②$\angle CAD$
③$\angle BOD$
④$\angle CAE$
図は動画内参照
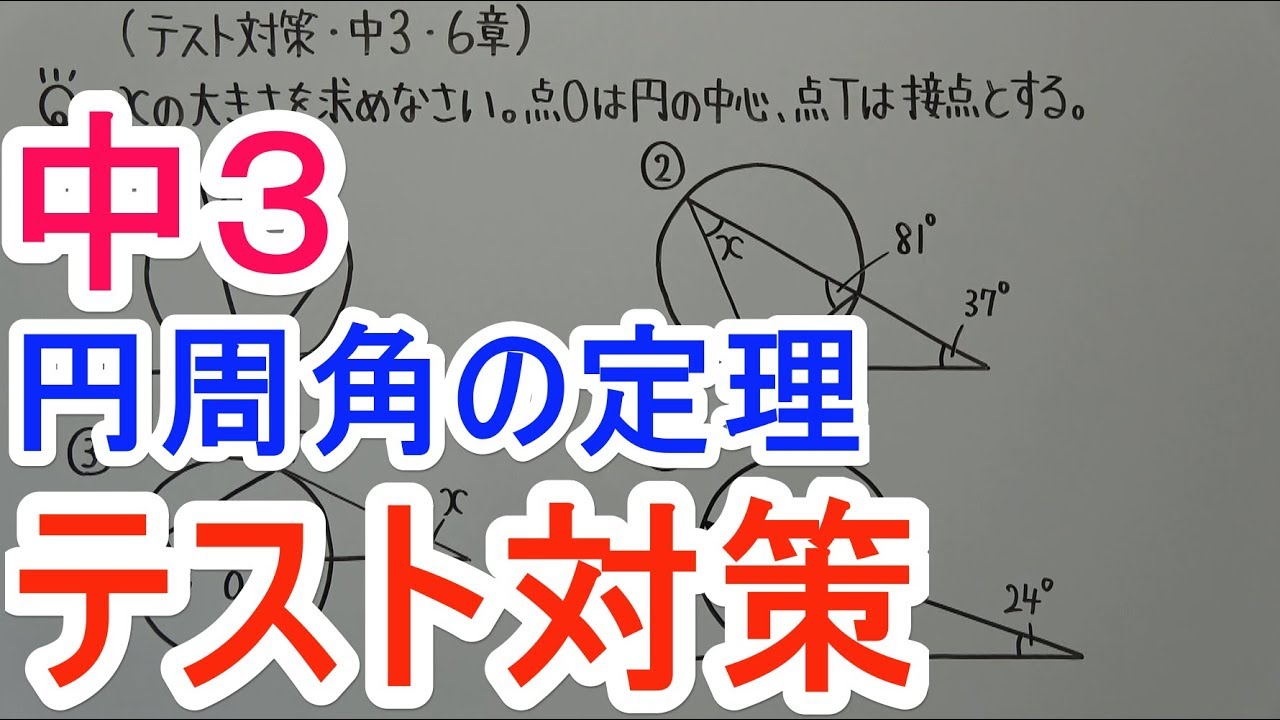
【テスト対策 中3】6章-2
単元：
#数学(中学生)#中３数学#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\angle x$の大きさを求めなさい。点$O$は円の中心、点$T$は接点とする。
図①～④は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。点$O$は円の中心、点$T$は接点とする。
図①～④は動画内参照
【テスト対策 中3】6章-1
単元：
#数学(中学生)#中３数学#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\angle x$の大きさを求めなさい。点$O$は円の中心とする。
図①～⑤は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。点$O$は円の中心とする。
図①～⑤は動画内参照
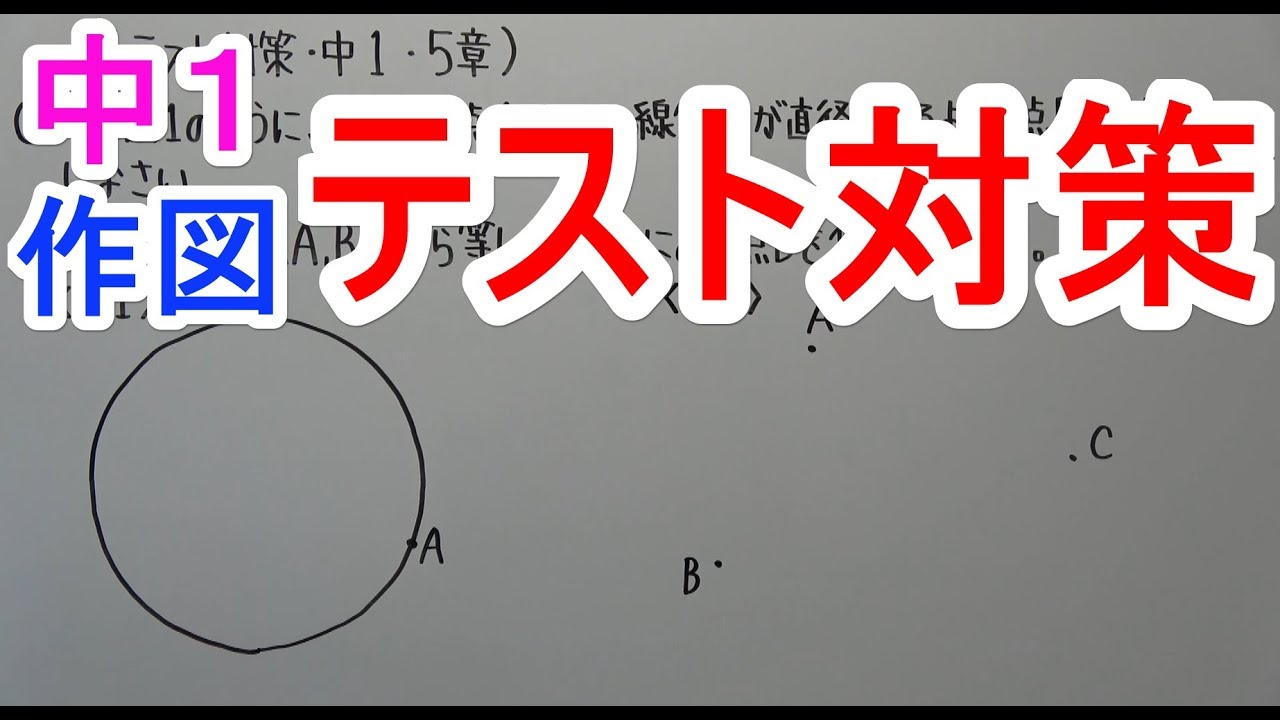
【テスト対策 中1】5章-4
単元：
#数学(中学生)#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①下の図1のように、円周上に点$A$がある。
線分$AB$が直径となるように点$B$を作図しなさい。
②下の図2の3点$A、B、C$から等しい距離にある点$D$を作図しなさい。
図は動画内参照
この動画を見る
①下の図1のように、円周上に点$A$がある。
線分$AB$が直径となるように点$B$を作図しなさい。
②下の図2の3点$A、B、C$から等しい距離にある点$D$を作図しなさい。
図は動画内参照
【高校受験対策】数学－死守２６
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#数と式#確率#円#一次不等式（不等式・絶対値のある方程式・不等式）#文章題#文章題その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-3+8$を計算しなさい.
②$2(2x - y) - (x - y)$を計算しなさい.
③$\sqrt{27}-\sqrt{63}$を計算しなさい.
④$(x + 5)(x - 3)$を展開しなさい.
⑤$a(b + 8) - (b + 8)$を因数分解しなさい.
⑥2次方程式 $x ^ 2 + x = 3$を解きなさい.
⑦右の図1の円$O$において,
$\angle x$と$\angle y$の大きさをそれぞれ求めなさい.
⑧鉛筆1本の値段を$a$円,ノート1冊の値段を$b$円とする.
「鉛筆3本とノート1冊の代金を払うと,
300円でおつりがもらえた」という数量の関係を,
不等式で表しなさい.ただし,値段は税込みとする.
⑨箱の中に,25本の当たりを含むたくさんのくじが入っている.
このくじをよくかき混ぜた後,48人がこの箱から1人1回ずつくじを引いたところ,
当たりが2本出た.箱の中に最初に入っていたくじの本数は,
およそ何本であったと推定できるか,求めなさい.
⑩ある水族館の入館料は,おとな3人と子ども2人で入ると4020円かかり,
おとな1人と子ども3人で入ると2600円かかる.
おとな1人,子ども1人の入館料をそれぞれ求めなさい.
ただし,入館料は税込みとする.
図は動画内参照
この動画を見る
①$-3+8$を計算しなさい.
②$2(2x - y) - (x - y)$を計算しなさい.
③$\sqrt{27}-\sqrt{63}$を計算しなさい.
④$(x + 5)(x - 3)$を展開しなさい.
⑤$a(b + 8) - (b + 8)$を因数分解しなさい.
⑥2次方程式 $x ^ 2 + x = 3$を解きなさい.
⑦右の図1の円$O$において,
$\angle x$と$\angle y$の大きさをそれぞれ求めなさい.
⑧鉛筆1本の値段を$a$円,ノート1冊の値段を$b$円とする.
「鉛筆3本とノート1冊の代金を払うと,
300円でおつりがもらえた」という数量の関係を,
不等式で表しなさい.ただし,値段は税込みとする.
⑨箱の中に,25本の当たりを含むたくさんのくじが入っている.
このくじをよくかき混ぜた後,48人がこの箱から1人1回ずつくじを引いたところ,
当たりが2本出た.箱の中に最初に入っていたくじの本数は,
およそ何本であったと推定できるか,求めなさい.
⑩ある水族館の入館料は,おとな3人と子ども2人で入ると4020円かかり,
おとな1人と子ども3人で入ると2600円かかる.
おとな1人,子ども1人の入館料をそれぞれ求めなさい.
ただし,入館料は税込みとする.
図は動画内参照
【高校受験対策】数学－図形１６
単元：
#数学(中学生)#中２数学#中３数学#円#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右図のように,円$O$の周上に4点,$A,B,C,D$がある.
円$O$の直径$AC$と,線分$BD$との交点を$E$とし,
線分$AD$上に$AB//FE$となる点$F$をとる.
また,$AB = 6\sqrt 3cm,AC = 12cm,AD=9cm,\angle ADB = 60°$とする.
次の各問いに答えなさい.
①線分$BC$の長さを求めなさい.
②$DF= a cm$とするとき,$EF$の長さを$a$の式で表しなさい.
③$△BCD∞△AFE$を証明しなさい.
④図の$\Box$の部分の面積を求めなさい.
ただし,円周率は$\pi$とする.
図は動画内参照
この動画を見る
右図のように,円$O$の周上に4点,$A,B,C,D$がある.
円$O$の直径$AC$と,線分$BD$との交点を$E$とし,
線分$AD$上に$AB//FE$となる点$F$をとる.
また,$AB = 6\sqrt 3cm,AC = 12cm,AD=9cm,\angle ADB = 60°$とする.
次の各問いに答えなさい.
①線分$BC$の長さを求めなさい.
②$DF= a cm$とするとき,$EF$の長さを$a$の式で表しなさい.
③$△BCD∞△AFE$を証明しなさい.
④図の$\Box$の部分の面積を求めなさい.
ただし,円周率は$\pi$とする.
図は動画内参照
【高校受験対策】数学－死守２５
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#２次方程式#円#文章題#文章題その他#表とグラフ#表とグラフ・集合#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-4-8$を計算しなさい.
②$\dfrac{1}{3}-\dfrac{3}{7}$を計算しなさい.
③$\sqrt{50}-\sqrt{32}$を計算しなさい.
④2次方程式$x^ 2 - 5x + 2 = 0$を解きなさい.
⑤図1のように,四角形$ABCD$の3つの頂点における外角が
わかっているとき,$\angle x$の大きさを求めなさい.
⑥図2のような半径$6cm$の半球の表面積と体積を求めなさい.
ただし,円周率は$\pi$とする.
⑦右の表は,あるクラスの1日の家庭での学習時間を
度数分布表にまとめたものである.
この表から$\Box$にあてはまる数と最頻値(モード) を求めなさい.
⑧ある家庭では,昨年1月の電気代と水道代の1日当たりの合計額は530円だった.
その後,家族で節電・節水を心がけたため,今年1月の1日当たりの額は,
昨年1月と比較して電気代は15%,水道代は10%減り,
1日当たりの合計額は460円となった.
昨年1月の1日当たりの電気代と水道代はそれぞれ何円か,求めなさい.
図は動画内参照
この動画を見る
①$-4-8$を計算しなさい.
②$\dfrac{1}{3}-\dfrac{3}{7}$を計算しなさい.
③$\sqrt{50}-\sqrt{32}$を計算しなさい.
④2次方程式$x^ 2 - 5x + 2 = 0$を解きなさい.
⑤図1のように,四角形$ABCD$の3つの頂点における外角が
わかっているとき,$\angle x$の大きさを求めなさい.
⑥図2のような半径$6cm$の半球の表面積と体積を求めなさい.
ただし,円周率は$\pi$とする.
⑦右の表は,あるクラスの1日の家庭での学習時間を
度数分布表にまとめたものである.
この表から$\Box$にあてはまる数と最頻値(モード) を求めなさい.
⑧ある家庭では,昨年1月の電気代と水道代の1日当たりの合計額は530円だった.
その後,家族で節電・節水を心がけたため,今年1月の1日当たりの額は,
昨年1月と比較して電気代は15%,水道代は10%減り,
1日当たりの合計額は460円となった.
昨年1月の1日当たりの電気代と水道代はそれぞれ何円か,求めなさい.
図は動画内参照
【高校受験対策】数学－死守２４
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#円#立体図形#立体切断#立体図形その他#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-7+9$を計算しなさい.
②$1+\left(-\dfrac{5}{6}\right)\div \dfrac{1}{3}$を計算しなさい.
③$8(x - y) + 6(x - 2y)$を計算しなさい.
④$\sqrt{27} - \dfrac{6}{\sqrt3}$を計算しなさい.
⑤$x(x + 2) - (x + 4)(x - 3)$を計算しなさい.
⑥絶対値が$2.5$より小さい整数はいくつあるか,求めなさい.
⑦2つの方程式$3x + y = 11$と$x + 3y = 1$両方にあてはまる$x,y$の値の組がある.
このとき,$x^2-y^2$の値を求めなさい.
⑧右の図のおうぎ形$OAB$は,半径$3cm$,中心角$90°$である.
このおうぎ形$OAB$を, $AD$を通る直線$\ell$を軸として1回転させてできる
立体の体積と表面積を求めなさい.
ただし,円周率は$\pi$とする.
⑨右の表は,ある中学校における男子15人の50m走の記録を
度数分布表に表したものである.
この表の8.5秒以上9.0秒未満の階級の相対度数を求めなさい.
図は動画内参照
この動画を見る
①$-7+9$を計算しなさい.
②$1+\left(-\dfrac{5}{6}\right)\div \dfrac{1}{3}$を計算しなさい.
③$8(x - y) + 6(x - 2y)$を計算しなさい.
④$\sqrt{27} - \dfrac{6}{\sqrt3}$を計算しなさい.
⑤$x(x + 2) - (x + 4)(x - 3)$を計算しなさい.
⑥絶対値が$2.5$より小さい整数はいくつあるか,求めなさい.
⑦2つの方程式$3x + y = 11$と$x + 3y = 1$両方にあてはまる$x,y$の値の組がある.
このとき,$x^2-y^2$の値を求めなさい.
⑧右の図のおうぎ形$OAB$は,半径$3cm$,中心角$90°$である.
このおうぎ形$OAB$を, $AD$を通る直線$\ell$を軸として1回転させてできる
立体の体積と表面積を求めなさい.
ただし,円周率は$\pi$とする.
⑨右の表は,ある中学校における男子15人の50m走の記録を
度数分布表に表したものである.
この表の8.5秒以上9.0秒未満の階級の相対度数を求めなさい.
図は動画内参照
【高校受験対策】数学－図形１５
単元：
#数学(中学生)#中２数学#中３数学#円#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①図1のように,$\stackrel{\huge\frown}{AB}$上に$\stackrel{\huge\frown}{AP}$と$\stackrel{\huge\frown}{PB}$の長さの比が$5:4$となるように
点$P$をとるとき,$\angle PAB$の大きさを求めなさい.
②図2のように,$AB$を直径とする円の周上に点$C$をとり,
直径$AB$を$B$の方に延長した直線上に点$D$をとります.
$CD =\dfrac{1}{2}AB,\angle BCD = 27°$のとき,
$\angle CAB$の大きさ$x$を求めなさい.
③図3で,線分$AB$は円$O$の直径で,
2点$C,D$は円$O$の周上にあり,$BC \perp OD$である.
また,点$E$は2直線$AC,BD$の交点である.
$\angle OBC=a°$のとき,$\angle CED$の大きさを$a$を用いて表せ.
図は動画内参照
この動画を見る
①図1のように,$\stackrel{\huge\frown}{AB}$上に$\stackrel{\huge\frown}{AP}$と$\stackrel{\huge\frown}{PB}$の長さの比が$5:4$となるように
点$P$をとるとき,$\angle PAB$の大きさを求めなさい.
②図2のように,$AB$を直径とする円の周上に点$C$をとり,
直径$AB$を$B$の方に延長した直線上に点$D$をとります.
$CD =\dfrac{1}{2}AB,\angle BCD = 27°$のとき,
$\angle CAB$の大きさ$x$を求めなさい.
③図3で,線分$AB$は円$O$の直径で,
2点$C,D$は円$O$の周上にあり,$BC \perp OD$である.
また,点$E$は2直線$AC,BD$の交点である.
$\angle OBC=a°$のとき,$\angle CED$の大きさを$a$を用いて表せ.
図は動画内参照
【高校受験対策】数学－死守２１
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#円#文章題#文章題その他#立体図形#体積・表面積・回転体・水量・変化のグラフ#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$7-(-5)$を計算しなさい.
②$(- 4) ^ 2 + 3 \times (- 2)$を計算しなさい.
③$\dfrac{3}{2} - 6y - \dfrac{1}{4} (3x-8y)$を計算しなさい.
④比例式$ 2:5 = (x - 2):(x + 7)$をみたす$x$の値を求めなさい.
⑤$\sqrt{45} - \sqrt{20} + \dfrac{15}{\sqrt5}$ を計算しなさい.
⑥$(x + 1)(x - 7) - 20$を因数分解しなさい.
⑦$a$の本の鉛筆を,$b$人の子どもに1人7本ずっ配ると3本余るとき,
$b$を$a$の式で表しなさい.
⑧ 右の図で,5点$A,B,C,D,E$は円$O$の円周上にあり,
$\angle BAC = 24°,\angle CED = 38°$,
$\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$である.
線分$BD$と線分$CE$の交点を$F$とするとき,$\angle CFD$の大きさを求めなさい.
⑨下の表には,6人の生徒$A~F$のそれぞれの身長から,
160cmをひいた値が示されている/
この表をもとに,これら6人の生徒の身長の平均を求めたところ161.5cmであった.
このとき,生徒$F$の身長を求めなさい.
⑩半径が3cmの球と体積の等しい円柱がある.
この円柱の底面の半径が4cmのとき,円柱の高さを求めなさい.
図は動画内参照
この動画を見る
①$7-(-5)$を計算しなさい.
②$(- 4) ^ 2 + 3 \times (- 2)$を計算しなさい.
③$\dfrac{3}{2} - 6y - \dfrac{1}{4} (3x-8y)$を計算しなさい.
④比例式$ 2:5 = (x - 2):(x + 7)$をみたす$x$の値を求めなさい.
⑤$\sqrt{45} - \sqrt{20} + \dfrac{15}{\sqrt5}$ を計算しなさい.
⑥$(x + 1)(x - 7) - 20$を因数分解しなさい.
⑦$a$の本の鉛筆を,$b$人の子どもに1人7本ずっ配ると3本余るとき,
$b$を$a$の式で表しなさい.
⑧ 右の図で,5点$A,B,C,D,E$は円$O$の円周上にあり,
$\angle BAC = 24°,\angle CED = 38°$,
$\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$である.
線分$BD$と線分$CE$の交点を$F$とするとき,$\angle CFD$の大きさを求めなさい.
⑨下の表には,6人の生徒$A~F$のそれぞれの身長から,
160cmをひいた値が示されている/
この表をもとに,これら6人の生徒の身長の平均を求めたところ161.5cmであった.
このとき,生徒$F$の身長を求めなさい.
⑩半径が3cmの球と体積の等しい円柱がある.
この円柱の底面の半径が4cmのとき,円柱の高さを求めなさい.
図は動画内参照
【高校受験対策】数学－証明６
単元：
#数学(中学生)#中２数学#中３数学#円#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように,線分$AB$を直径とする円$O$の円周上に,点$C$をとります.
円$O$と,$CO$の延長との交点を$D$とし,
点$C$を通る円$O$の接線と$\angle BOC$の二等分線との交点を$E$とします.
このとき,次の問いに答えなさい.
①$OB=4cm, \angle BOD = 120°$のとき,
線分$BD$の長さを求めなさい.
②$△ABC ∞ OEC$を証明しなさい.
図は動画内参照
この動画を見る
右の図のように,線分$AB$を直径とする円$O$の円周上に,点$C$をとります.
円$O$と,$CO$の延長との交点を$D$とし,
点$C$を通る円$O$の接線と$\angle BOC$の二等分線との交点を$E$とします.
このとき,次の問いに答えなさい.
①$OB=4cm, \angle BOD = 120°$のとき,
線分$BD$の長さを求めなさい.
②$△ABC ∞ OEC$を証明しなさい.
図は動画内参照
【高校受験対策】数学－死守１６
単元：
#数学(中学生)#中２数学#中３数学#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#確率#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問いに答えなさい.
①$-4+(-3)$を計算しなさい.
②$-\dfrac{1}{7}+\dfrac{2}{5}$を計算しなさい.
③$16ab^2 \div 8ab$を計算しなさい.
④$\sqrt{54}-\dfrac{42}{\sqrt6}$を計算しなさい.
⑤$(x+2)(x+3)-(x+4)^2$を計算しなさい.
⑥$(x-5)^2-7(x-5)+12$を因数分解しなさい.
⑦2次方程式$5x^2-3x-1=0$を解きなさい.
⑧$x=3-\sqrt7$のとき,
$x^2-6x+9$の値を求めなさい.
⑨関数$y=ax^2$について,
$x$の値が$-3$から$-1$まで増加するときの変化の割合が$-3$であった.
このとき,$a$の値を求めなさい.
⑩1から6までの目の出る大,小2つのさいころを同時に1回投げるとき,
出た目の数の和が9以上とならない確率を求めなさい.
⑪半径が$2cm$である球の体積を$Pcm^3$,l
半径が$3cm$である球の体積を$Qcm^3$とするとき,
$P$と$Q$の比を最も簡単な整数の比で表しなさい。.
ただし,円周率は$\pi$とする.
⑫ 右の図において,線分$AB$は円$O$の直径であり,
2点$C,D$は円$O$の周上の点である.
このとき,$△ABC$の大きさを求めなさい.
この動画を見る
次の各問いに答えなさい.
①$-4+(-3)$を計算しなさい.
②$-\dfrac{1}{7}+\dfrac{2}{5}$を計算しなさい.
③$16ab^2 \div 8ab$を計算しなさい.
④$\sqrt{54}-\dfrac{42}{\sqrt6}$を計算しなさい.
⑤$(x+2)(x+3)-(x+4)^2$を計算しなさい.
⑥$(x-5)^2-7(x-5)+12$を因数分解しなさい.
⑦2次方程式$5x^2-3x-1=0$を解きなさい.
⑧$x=3-\sqrt7$のとき,
$x^2-6x+9$の値を求めなさい.
⑨関数$y=ax^2$について,
$x$の値が$-3$から$-1$まで増加するときの変化の割合が$-3$であった.
このとき,$a$の値を求めなさい.
⑩1から6までの目の出る大,小2つのさいころを同時に1回投げるとき,
出た目の数の和が9以上とならない確率を求めなさい.
⑪半径が$2cm$である球の体積を$Pcm^3$,l
半径が$3cm$である球の体積を$Qcm^3$とするとき,
$P$と$Q$の比を最も簡単な整数の比で表しなさい。.
ただし,円周率は$\pi$とする.
⑫ 右の図において,線分$AB$は円$O$の直径であり,
2点$C,D$は円$O$の周上の点である.
このとき,$△ABC$の大きさを求めなさい.