 中3数学
中3数学
 中3数学
中3数学
サウンドを聞きながら数学が好きになる!~全国入試問題解法 #数学 #数検 #高校入試 #勉強 #ライブ

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
サウンドを聞きながら数学が好きになる!
直角三角形$ABC$において
$a^2 + b^2 = c^2$
が成り立つ。
【$BC = a$】
【$CA=b$】
【$ AB=c$】
図を用いて 証明せよ。
※図は動画内参照
この動画を見る
サウンドを聞きながら数学が好きになる!
直角三角形$ABC$において
$a^2 + b^2 = c^2$
が成り立つ。
【$BC = a$】
【$CA=b$】
【$ AB=c$】
図を用いて 証明せよ。
※図は動画内参照
分数式の計算

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$\displaystyle \frac{x^2-2}{x-1}+\displaystyle \frac{1}{x-1}=??$
この動画を見る
以下を求めよ。
$\displaystyle \frac{x^2-2}{x-1}+\displaystyle \frac{1}{x-1}=??$
【数学】中高一貫校問題集2幾何178:三平方の定理:平面図形 2円の交点の長さ

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径が1cmの円Oと半径が$\sqrt{2}$cmの円O´が2点A,Bで交わっている。中心間の距離がOO´=2cmであるとき、線分ABの長さを求めなさい。
この動画を見る
半径が1cmの円Oと半径が$\sqrt{2}$cmの円O´が2点A,Bで交わっている。中心間の距離がOO´=2cmであるとき、線分ABの長さを求めなさい。
【数学】中高一貫校問題集2幾何177:三平方の定理:平面図形 共通接線の長さ2
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
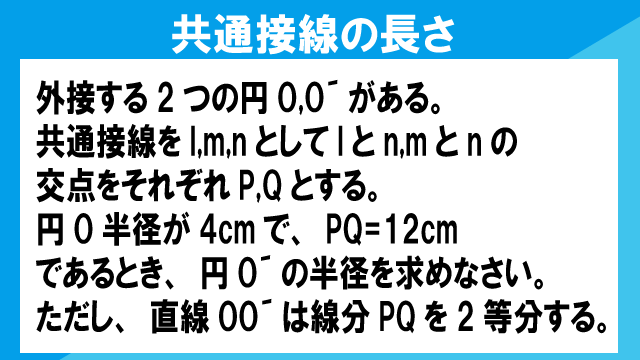
右の図のように、外接する2つの円O,O´がある。共通接線をl,m,nとしてlとn,mとnの交点をそれぞれP,Qとする。円O半径が4cmで、PQ=12cmであるとき、円O´の半径を求めなさい。ただし、直線OO´は線分PQを2等分する。
この動画を見る
右の図のように、外接する2つの円O,O´がある。共通接線をl,m,nとしてlとn,mとnの交点をそれぞれP,Qとする。円O半径が4cmで、PQ=12cmであるとき、円O´の半径を求めなさい。ただし、直線OO´は線分PQを2等分する。
これできる?

見た目であなたは騙される
連立方程式だけど2次式 清風南海

単元:
#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
以下の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(2x^2+4x)-(y^2-4y)=2 \\
(x^2+2x)+(y^2-4y)=-5
\end{array}
\right.
\end{eqnarray}$
出典:清風南海高等学校
この動画を見る
以下の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(2x^2+4x)-(y^2-4y)=2 \\
(x^2+2x)+(y^2-4y)=-5
\end{array}
\right.
\end{eqnarray}$
出典:清風南海高等学校
素数に関する整数問題 高校入試問題としては難問です 海城高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$P-x^3y-xy-\displaystyle \frac{7x^3}{2}+\displaystyle \frac{7x}{2}$
$P$の値が素数となるような正の整数$x,y$の値の組($x,y$)をすべて求めよ。
出典:海城高校
この動画を見る
$P-x^3y-xy-\displaystyle \frac{7x^3}{2}+\displaystyle \frac{7x}{2}$
$P$の値が素数となるような正の整数$x,y$の値の組($x,y$)をすべて求めよ。
出典:海城高校
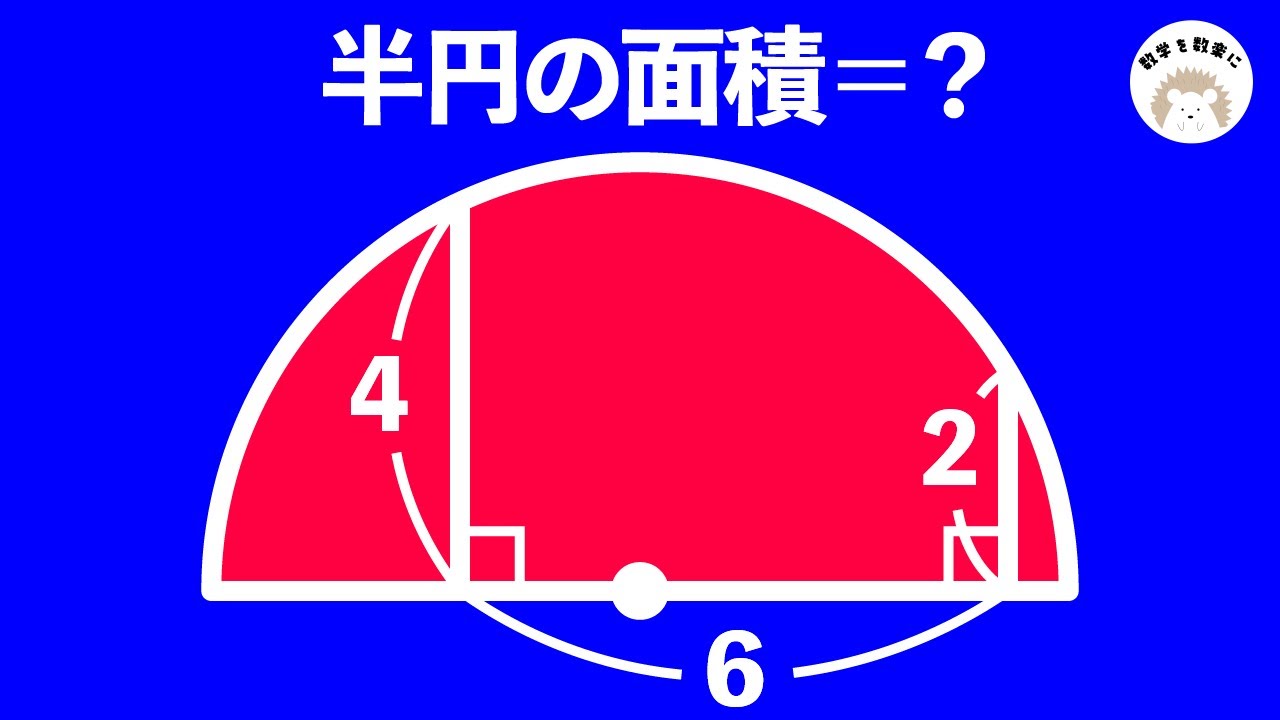
半円の面積🟰❓ (area of semicircle🟰❓)
ルートのかけ算はこうする?

平方根の計算 成蹊高校

単元:
#中3数学#平方根#高校入試過去問(数学)#成蹊高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$\sqrt{ 33^4-22^4-11^4 }$
出典:成蹊高校
この動画を見る
以下を求めよ。
$\sqrt{ 33^4-22^4-11^4 }$
出典:成蹊高校
放物線と正三角形 開成高校

単元:
#中3数学#2次関数#高校入試過去問(数学)#開成高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、正三角形$\rm{ABC}$の1辺の長さを求めよ。
出典:開成高校
この動画を見る
動画内の図を参照し、正三角形$\rm{ABC}$の1辺の長さを求めよ。
出典:開成高校
気付けば気持ちいいよ。正方形の周の長さの和🟰❓

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの正方形の面積の差は$51cm^2$
2つの正方形の周の長さの差は$12cm$
2つの正方形の周の長さの和は$?cm$
この動画を見る
2つの正方形の面積の差は$51cm^2$
2つの正方形の周の長さの差は$12cm$
2つの正方形の周の長さの和は$?cm$
台形の中の面積比

数学を数楽に

ボボボーボ・ボーボボを因数分解すると?

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ボボボーボ・ボーボボを因数分解すると?
この動画を見る
下記質問の解説動画です
ボボボーボ・ボーボボを因数分解すると?
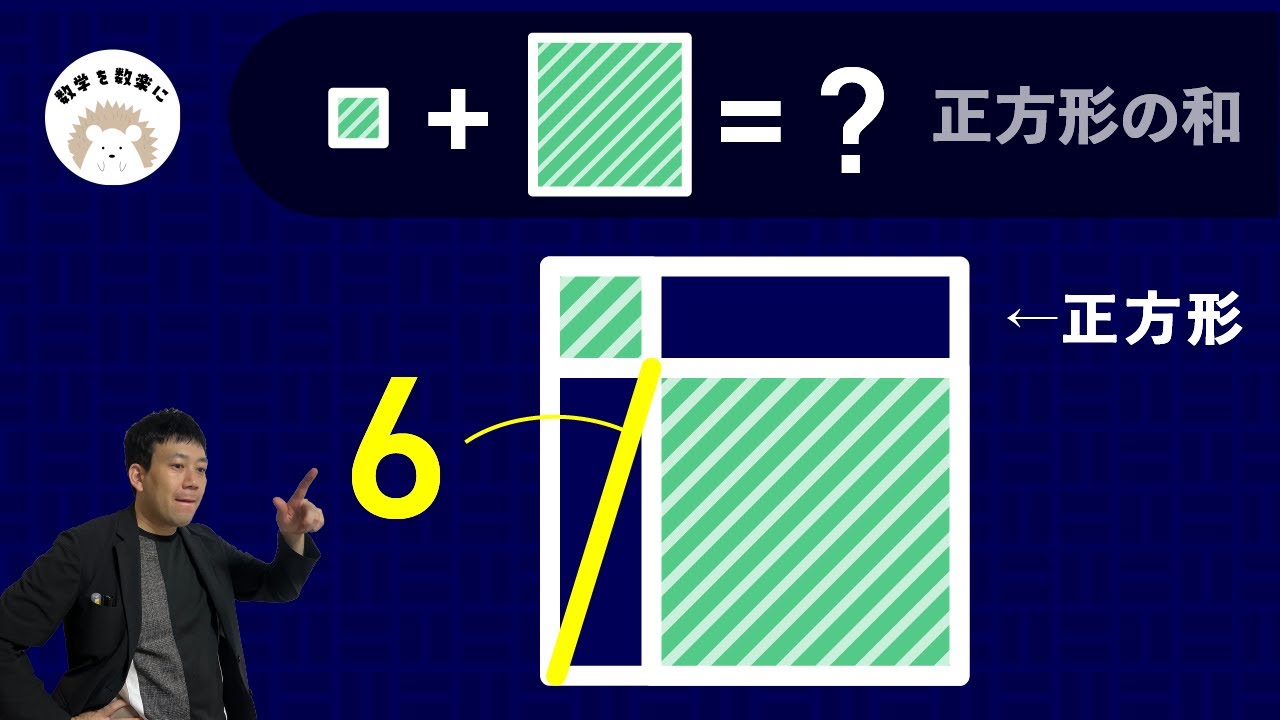
気付けば一瞬!!正方形の中の正方形の面積の和
数学を数楽に

2次方程式を解け

中学生も解ける!?5次方程式を解け

乗法公式を面積図で

ルートの計算
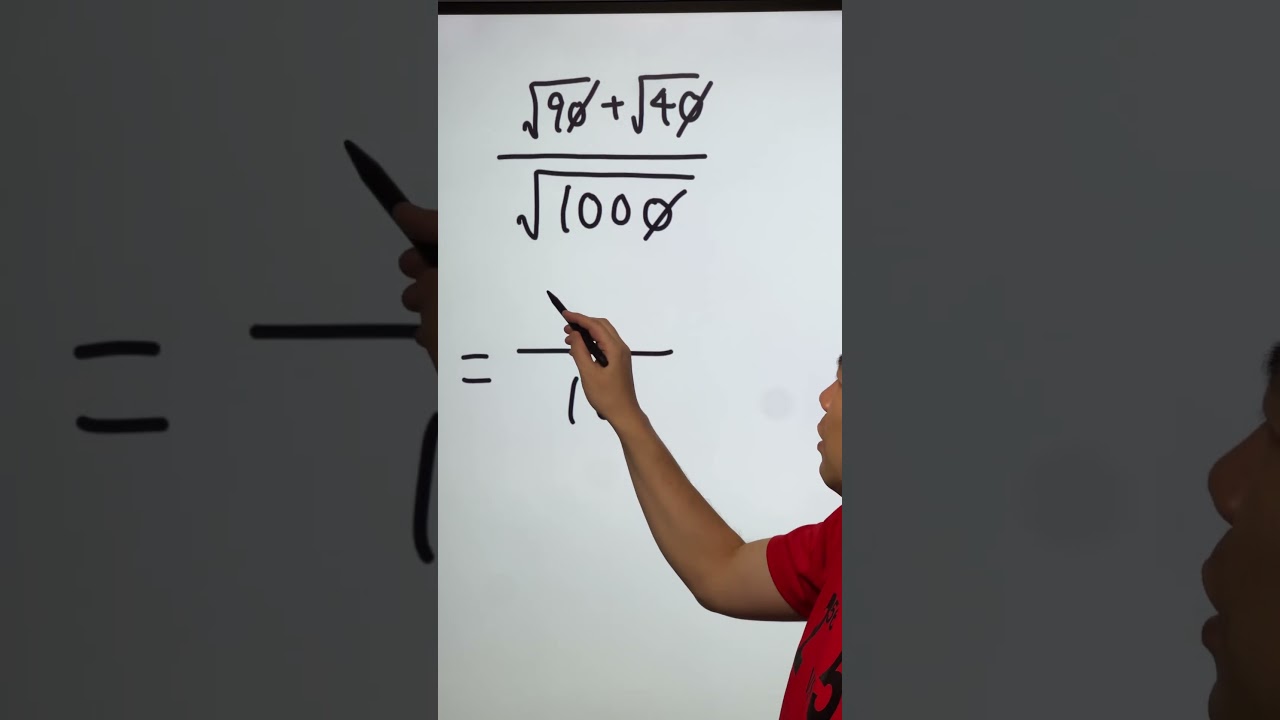
単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{\sqrt{ 90 }+\sqrt{ 40 }}{{ \sqrt{ 1000 } }}=??$
この動画を見る
$\displaystyle \frac{\sqrt{ 90 }+\sqrt{ 40 }}{{ \sqrt{ 1000 } }}=??$
正方形の面積🟰❓

【数学】中高一貫校問題集2幾何176:三平方の定理:平面図形 共通接線の長さ1

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)図1で、2つの円O,O´は外接しており、A,Bは共通接線の接点である。O,O´の半径がそれぞれ5cm,2cmであるとき、線分ABの長さを求めなさい。
(2)図2で、A,Bは、2つの円O,O´の共通接線の接点である。O,O´の半径がそれぞれ5cm,3cmで、2つの円の中心間の距離が10cmであるとき、線分ABの長さを求めなさい。
この動画を見る
(1)図1で、2つの円O,O´は外接しており、A,Bは共通接線の接点である。O,O´の半径がそれぞれ5cm,2cmであるとき、線分ABの長さを求めなさい。
(2)図2で、A,Bは、2つの円O,O´の共通接線の接点である。O,O´の半径がそれぞれ5cm,3cmで、2つの円の中心間の距離が10cmであるとき、線分ABの長さを求めなさい。
ルートの計算 2024洛南

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#洛南高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$(1+\sqrt{ 2 }+\sqrt{ 4 }+\sqrt{ 8 }+\sqrt{ 16 }+\sqrt{ 32 })\times(1-\sqrt{ 2 }+\sqrt{ 4 }-\sqrt{ 8 }+\sqrt{ 16 }-\sqrt{ 32 })$
この動画を見る
以下を求めよ。
$(1+\sqrt{ 2 }+\sqrt{ 4 }+\sqrt{ 8 }+\sqrt{ 16 }+\sqrt{ 32 })\times(1-\sqrt{ 2 }+\sqrt{ 4 }-\sqrt{ 8 }+\sqrt{ 16 }-\sqrt{ 32 })$
【数学】中高一貫校問題集2幾何175:三平方の定理:平面図形 四角形の面積

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(代数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の四角形ABCDの面積を求めなさい。ただし、(1)で、AD//BCである。
この動画を見る
次の四角形ABCDの面積を求めなさい。ただし、(1)で、AD//BCである。
【数学】中高一貫校問題集2幾何174:三平方の定理:平面図形 三角形の面積+ヘロンの公式
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の△ABCの面積を求めなさい。(3辺の長さが2cm、3cm、4cmの三角形の面積を求めよ)
この動画を見る
次の△ABCの面積を求めなさい。(3辺の長さが2cm、3cm、4cmの三角形の面積を求めよ)
長方形の面積🟰❓
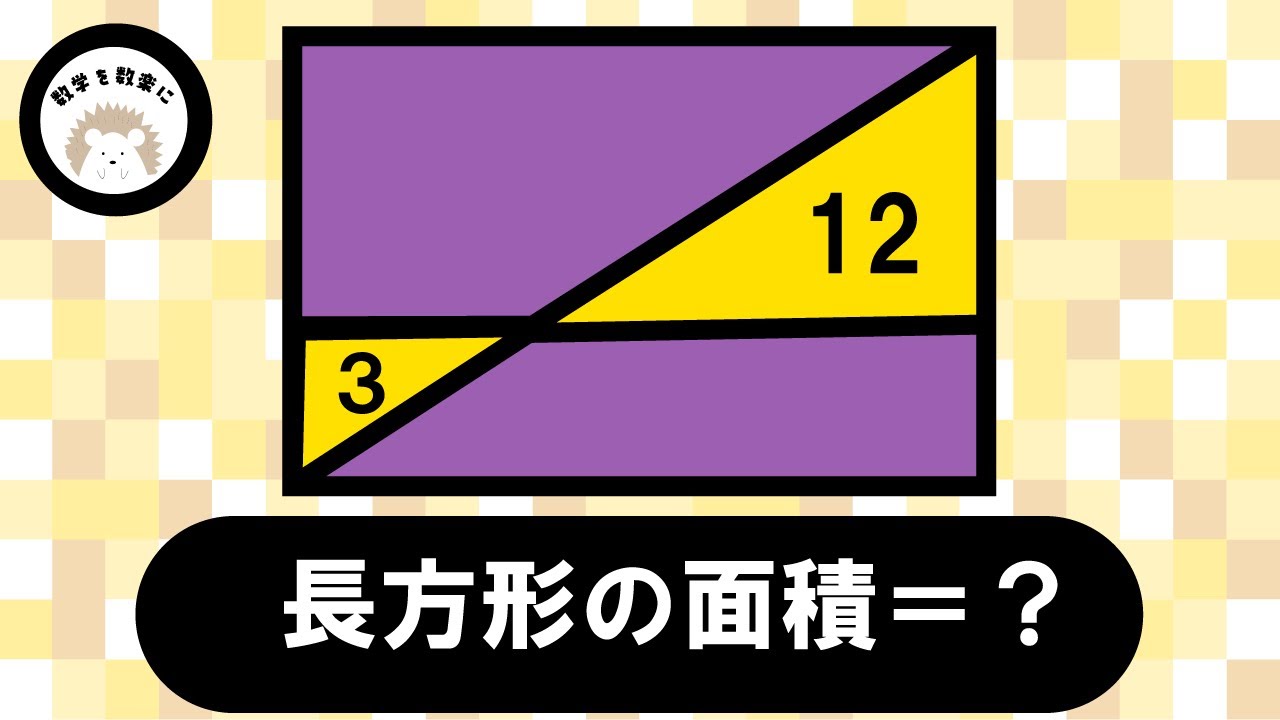
気付けば一瞬!!2通りで解説
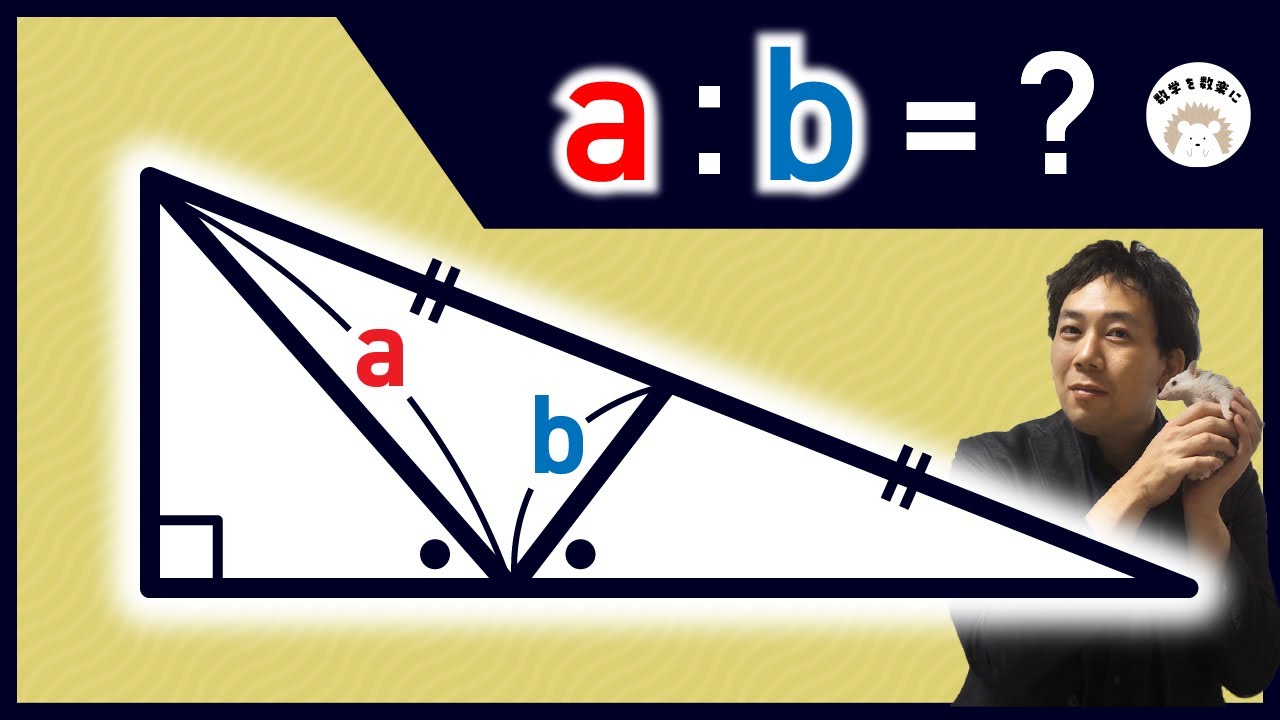
この手があったか!分母の有理化

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{21}{\sqrt 7}=$
この動画を見る
$\frac{21}{\sqrt 7}=$
