数学(中学生)
数学(中学生)
【テスト対策 中1】5章-4
単元：
#数学(中学生)#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①下の図1のように、円周上に点$A$がある。
線分$AB$が直径となるように点$B$を作図しなさい。
②下の図2の3点$A、B、C$から等しい距離にある点$D$を作図しなさい。
図は動画内参照
この動画を見る
①下の図1のように、円周上に点$A$がある。
線分$AB$が直径となるように点$B$を作図しなさい。
②下の図2の3点$A、B、C$から等しい距離にある点$D$を作図しなさい。
図は動画内参照
【テスト対策 中1】5章-2
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の$\Box$にあてはまることばを書きなさい。
・平面上で、図形をある点$O$を中心にして一定の角度だけまわすことを$\Box$といい、
点$O$を$\Box$という。
その中で、180℃の$\Box$を$\Box$という。
・平面上で、図形をある直線$\ell$を折り目として折り返すことを$\Box$といい、
直線$\ell$を$\Box$という。
$\Box$で移りあう図形は、$\Box$について$\Box$対で、
対応する点を結んだ線分は$\Box$と$\Box$に交わり、
その交点で$\Box$される。
この動画を見る
◎次の$\Box$にあてはまることばを書きなさい。
・平面上で、図形をある点$O$を中心にして一定の角度だけまわすことを$\Box$といい、
点$O$を$\Box$という。
その中で、180℃の$\Box$を$\Box$という。
・平面上で、図形をある直線$\ell$を折り目として折り返すことを$\Box$といい、
直線$\ell$を$\Box$という。
$\Box$で移りあう図形は、$\Box$について$\Box$対で、
対応する点を結んだ線分は$\Box$と$\Box$に交わり、
その交点で$\Box$される。
【テスト対策 中1】5章-1
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の$\Box$にあてはまることばや記号を書きなさい。
・2直線$AB、CD$が交わってできる角が直角のとき、
$AB$と$CD$は$\Box$であるといい、 ②$AB\Box CD$と表す。
また、2直線$\ell、m$が交わらないとき、$\ell$は$m$はといい、$AB \Box CD$と表す。
・図形の形と大きさを変えないで、位置だけを変えることを$\Box$という。
・平面上で、図形を一定の方向に、一定の長さだけずらすことを$\Box$といい、
このとき、対応する2点を結ぶ線分は、それぞれ$\Box$で長さが$\Box$。
この動画を見る
次の$\Box$にあてはまることばや記号を書きなさい。
・2直線$AB、CD$が交わってできる角が直角のとき、
$AB$と$CD$は$\Box$であるといい、 ②$AB\Box CD$と表す。
また、2直線$\ell、m$が交わらないとき、$\ell$は$m$はといい、$AB \Box CD$と表す。
・図形の形と大きさを変えないで、位置だけを変えることを$\Box$という。
・平面上で、図形を一定の方向に、一定の長さだけずらすことを$\Box$といい、
このとき、対応する2点を結ぶ線分は、それぞれ$\Box$で長さが$\Box$。
【テスト対策 中2】5章-6
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図のように、正三角形$ABC$において辺$AC$上に点$D$をとり、
$AE//BC$、$AD=AE$となるように点$E$をとる。
このとき、$BD=CE$であることを証明しなさい。
図は動画内参照
この動画を見る
①右の図のように、正三角形$ABC$において辺$AC$上に点$D$をとり、
$AE//BC$、$AD=AE$となるように点$E$をとる。
このとき、$BD=CE$であることを証明しなさい。
図は動画内参照
【テスト対策 中2】5章-5
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①図1は、平行四辺形$ABCD$で$BD//EF$である。
$△ABE$と面積が等しい三角形をすべて答えなさい。
②図2は、平行四辺形$ABCD$で辺$BC$の延長上に点$P$をとり、
線分$AP$と辺$CD$との交点を$Q$とした図である。
このとき、$△BCQ$と面積が等しい三角形をすべて答えなさい。
図は動画内参照
この動画を見る
①図1は、平行四辺形$ABCD$で$BD//EF$である。
$△ABE$と面積が等しい三角形をすべて答えなさい。
②図2は、平行四辺形$ABCD$で辺$BC$の延長上に点$P$をとり、
線分$AP$と辺$CD$との交点を$Q$とした図である。
このとき、$△BCQ$と面積が等しい三角形をすべて答えなさい。
図は動画内参照
【テスト対策 中2】5章-4
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図は、$AB\lt AD$である長方形$ABCD$を、
対角線$AC$を折り目として折り返し、頂点$D$が移った点を$E$、
辺$BC$と線分$AE$の交点を$F$としたものである。
このとき、三角形$AFC$は二等辺三角形であることを証明しなさい。
図は動画内参照
この動画を見る
右の図は、$AB\lt AD$である長方形$ABCD$を、
対角線$AC$を折り目として折り返し、頂点$D$が移った点を$E$、
辺$BC$と線分$AE$の交点を$F$としたものである。
このとき、三角形$AFC$は二等辺三角形であることを証明しなさい。
図は動画内参照
【テスト対策 中2】5章-3
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\angle x$の大きさを求めなさい。
①$AD=CD,CD$は$\angle ACB$の二等分線
②$ABCD$は平行四辺形、$BE=CE$
③$ABCD$はひし形、$AD=AE$
④$CD=CE$
$BFC=90°$
図は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。
①$AD=CD,CD$は$\angle ACB$の二等分線
②$ABCD$は平行四辺形、$BE=CE$
③$ABCD$はひし形、$AD=AE$
④$CD=CE$
$BFC=90°$
図は動画内参照
【テスト対策 中2】5章-2
単元：
#数学(中学生)#中２数学#平行と合同
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図において、$AB=CD,AB /\!/ CD$のとき、
$AO=CO$であることを証明しなさい。
図は動画内参照
この動画を見る
右の図において、$AB=CD,AB /\!/ CD$のとき、
$AO=CO$であることを証明しなさい。
図は動画内参照
【テスト対策 中2】5章-1
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\angle x$の大きさを求めなさい。
①$AB=AC,BD$は$\angle ABC$の二等分線
②$AD=BD,BC /\!/ DE,BE$は$\angle ABC$の二等分線
③$AB=AC$
$AD=AE$
④$AB=AC$
$\ell /\!/ m$
図は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。
①$AB=AC,BD$は$\angle ABC$の二等分線
②$AD=BD,BC /\!/ DE,BE$は$\angle ABC$の二等分線
③$AB=AC$
$AD=AE$
④$AB=AC$
$\ell /\!/ m$
図は動画内参照
【テスト対策 中3】5章-8
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、平行四辺形$ABCD$の辺$BC、CD$上にそれぞれ点$E、F$をとり、
$BE:EC =2 :1、CF:FD=2:1$とする。
直線$AE、AF$と対角線$BD$との交点をそれぞれ$P、Q$とする。
また、平行四辺形$ABCD$の面積を$S$とする。
①$AD: BE$を求めなさい。
②$AQ:QF$を求めなさい。
③$△PBE$の面積を$S$で表しなさい。
④$△AQD$の面積を$S$で表しなさい。
図は動画内参照
この動画を見る
右の図のように、平行四辺形$ABCD$の辺$BC、CD$上にそれぞれ点$E、F$をとり、
$BE:EC =2 :1、CF:FD=2:1$とする。
直線$AE、AF$と対角線$BD$との交点をそれぞれ$P、Q$とする。
また、平行四辺形$ABCD$の面積を$S$とする。
①$AD: BE$を求めなさい。
②$AQ:QF$を求めなさい。
③$△PBE$の面積を$S$で表しなさい。
④$△AQD$の面積を$S$で表しなさい。
図は動画内参照
【テスト対策 中3】5章-7
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1で、四角形$ABCD$は$AD/\!/ BC、 \angle ABC = 90°$の台形で、
$E$は線分$AC$と$DB$との交点である。
$AB=BC=6cm、 AD=3cm$のとき、$△BCE$の面積を求めなさい。
② 右の図2において、$AB=5cm、BC=4cm、CD=2cm、\angle ABC= \angle BCD = 90°$である。
このとき、$△BCE$の面積を求めなさい。
図は動画内参照
この動画を見る
①右の図1で、四角形$ABCD$は$AD/\!/ BC、 \angle ABC = 90°$の台形で、
$E$は線分$AC$と$DB$との交点である。
$AB=BC=6cm、 AD=3cm$のとき、$△BCE$の面積を求めなさい。
② 右の図2において、$AB=5cm、BC=4cm、CD=2cm、\angle ABC= \angle BCD = 90°$である。
このとき、$△BCE$の面積を求めなさい。
図は動画内参照
【テスト対策 中3】5章-6
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、$AB=3cm、BC=4cm$の平行四辺形があり、
辺$AD$上に点$E$、辺$BC$上に点$F$、辺$CD$上に点$G$を
それぞれ$AE=BF=DG=1cm$となるようにとる。
また、線分$EF$と線分$AC$との交点を$H$、線分$EF$と線分$BG$との交点を$I$とする。
このとき、次の線分の長さを求めなさい。
①線分$FI$
②線分$HI$
図は動画内参照
この動画を見る
右の図のように、$AB=3cm、BC=4cm$の平行四辺形があり、
辺$AD$上に点$E$、辺$BC$上に点$F$、辺$CD$上に点$G$を
それぞれ$AE=BF=DG=1cm$となるようにとる。
また、線分$EF$と線分$AC$との交点を$H$、線分$EF$と線分$BG$との交点を$I$とする。
このとき、次の線分の長さを求めなさい。
①線分$FI$
②線分$HI$
図は動画内参照
【テスト対策 中3】5章-5
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、平行四辺形$ABCD$において、
辺$AB$上の$AE:EB=2:1$である点を$E$、辺$AD$の中点を$F$、
線分$AC$と線分$EF$との交点を$G$とする。
$\angle AFE = 30° ∠BCE=11°、CG=4cm$のとき、次の問いに答えなさい。
①$∠CEF$の大きさを求めなさい。
②線分$AG$の長さを求めなさい。
図は動画内参照
この動画を見る
右の図のように、平行四辺形$ABCD$において、
辺$AB$上の$AE:EB=2:1$である点を$E$、辺$AD$の中点を$F$、
線分$AC$と線分$EF$との交点を$G$とする。
$\angle AFE = 30° ∠BCE=11°、CG=4cm$のとき、次の問いに答えなさい。
①$∠CEF$の大きさを求めなさい。
②線分$AG$の長さを求めなさい。
図は動画内参照
【テスト対策 中3】5章-4
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1は、長方形を折り返した図である。
このとき、$DF$の長さを求めなさい。
②右の図2は、1辺の長さが9の正方形を折り返した図である。
このとき、$HI$の長さを求めなさい。
図は動画内参照
この動画を見る
①右の図1は、長方形を折り返した図である。
このとき、$DF$の長さを求めなさい。
②右の図2は、1辺の長さが9の正方形を折り返した図である。
このとき、$HI$の長さを求めなさい。
図は動画内参照
【テスト対策 中3】5章-3
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図の$△ABC$で、点$D、E$は辺$AB$を3等分する点で、
点$F$は辺$AC$の中点です。
また、点$G$は$DF$を延長した直線と$BC$を延長した直線の交点で、
$CE=6cm$です。
①$DF$の長さを求めなさい。
②$BC=CG$を証明しなさい。
③$FG$の長さを求めなさい。
図は動画内参照
この動画を見る
右の図の$△ABC$で、点$D、E$は辺$AB$を3等分する点で、
点$F$は辺$AC$の中点です。
また、点$G$は$DF$を延長した直線と$BC$を延長した直線の交点で、
$CE=6cm$です。
①$DF$の長さを求めなさい。
②$BC=CG$を証明しなさい。
③$FG$の長さを求めなさい。
図は動画内参照
【テスト対策 中3】5章-2
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1で、$x,y$の値をそれぞれ求めなさい。
②右の図2で、四角形$ABCD$は$AD /\!/ BC$の台形で、
$EF /\!/ BC$である。$AD=3,EF=8,BC=11,EB=4$のとき、
$AE$の値を求めなさい。
図は動画内参照
この動画を見る
①右の図1で、$x,y$の値をそれぞれ求めなさい。
②右の図2で、四角形$ABCD$は$AD /\!/ BC$の台形で、
$EF /\!/ BC$である。$AD=3,EF=8,BC=11,EB=4$のとき、
$AE$の値を求めなさい。
図は動画内参照
【テスト対策 中3】5章-1
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で、四角形$ABCD∞$四角形$EFGH$である。
次の問いに答えなさい。
①相似比を求めなさい。
②辺$FG$の長さを求めなさい。
③$\angle F$の大きさを求めなさい。
④$\angle c$の大きさを求めなさい。
図は動画内参照
この動画を見る
右の図で、四角形$ABCD∞$四角形$EFGH$である。
次の問いに答えなさい。
①相似比を求めなさい。
②辺$FG$の長さを求めなさい。
③$\angle F$の大きさを求めなさい。
④$\angle c$の大きさを求めなさい。
図は動画内参照
【高校数学】数Ⅲ-51 分数関数とそのグラフ②
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の関数のグラフをかけ。
また、その漸近線を求めよ。
①$y=\dfrac{-2x+1}{x-1}$
②$y=\dfrac{-2x+5}{2x-1}$
図は動画内参照
この動画を見る
次の関数のグラフをかけ。
また、その漸近線を求めよ。
①$y=\dfrac{-2x+1}{x-1}$
②$y=\dfrac{-2x+5}{2x-1}$
図は動画内参照
【高校数学】数Ⅲ-50 分数関数とそのグラフ①
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の関数のグラフをかけ。
また、その漸近線を求めよ。
①$y=\dfrac{1}{2x}$
②$y=\dfrac{3}{x+3}-1$
③$y=\dfrac{3}{x-1}+2$
図は動画内参照
この動画を見る
次の関数のグラフをかけ。
また、その漸近線を求めよ。
①$y=\dfrac{1}{2x}$
②$y=\dfrac{3}{x+3}-1$
③$y=\dfrac{3}{x-1}+2$
図は動画内参照
【テスト対策 中1】4章-6
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図において、①は関数$y=ax$、②は関数$y=\dfrac{18}{x}$のグラフである。
点$A$は①と②の交点で、その$y$座標は6である。
このとき、次の問いに答えなさい。
(1)点$A$の座標を求めなさい。
(2)定数$a$の値を求めなさい。
(3)②のグラフ上の点で、$x$座標と$y$座標がともに整数となる点は
全部で何個あるか求めなさい。
(4)点$A$から$x$軸、$y$軸にひいた垂線が$x$軸、$y$軸と交わる点をそれぞれ
$B、C$とし、①のグラフ上に点$P$、$y$軸上に$y$標が8である点をとる。
三角形$OPQ$の面積が四角形$OBAC$の面積と等しくなるとき、
点$P$の座標をすべて求めなさい。
図は動画内参照
この動画を見る
右の図において、①は関数$y=ax$、②は関数$y=\dfrac{18}{x}$のグラフである。
点$A$は①と②の交点で、その$y$座標は6である。
このとき、次の問いに答えなさい。
(1)点$A$の座標を求めなさい。
(2)定数$a$の値を求めなさい。
(3)②のグラフ上の点で、$x$座標と$y$座標がともに整数となる点は
全部で何個あるか求めなさい。
(4)点$A$から$x$軸、$y$軸にひいた垂線が$x$軸、$y$軸と交わる点をそれぞれ
$B、C$とし、①のグラフ上に点$P$、$y$軸上に$y$標が8である点をとる。
三角形$OPQ$の面積が四角形$OBAC$の面積と等しくなるとき、
点$P$の座標をすべて求めなさい。
図は動画内参照
【テスト対策 中1】4章-5
単元：
#数学(中学生)#中２数学#1次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、関数$y=ax$のグラフと2点$A(3,6),B(7,0)$がある。
次の問いに答えなさい。
①$\triangle AOB$の面積を求めなさい。
②関数$y=ax$が$\triangle AOB$の面積を2等分するとき、
$a$の値を求めなさい。
図は動画内参照
この動画を見る
右の図のように、関数$y=ax$のグラフと2点$A(3,6),B(7,0)$がある。
次の問いに答えなさい。
①$\triangle AOB$の面積を求めなさい。
②関数$y=ax$が$\triangle AOB$の面積を2等分するとき、
$a$の値を求めなさい。
図は動画内参照
【テスト対策 中1】4章-4
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$y$は$x$に比例し、$x = 3$のとき$y=6$である。
また、$x$の変域が$-4≦ x \leqq 3$のとき、その変域は$a\leqq y\leqq b$である。
$a、b$の値を求めよ。
②$y$は$x$に比例し、$ x = 2$ のとき$y=-5$である。
また、$x$の変域が$-6≦x≦-4$のとき、 $y$の変域を求めなさい。
③$y$は$x$に反比例し、$x=-4$のとき$y=-6$である。
また、$x$の変域が$2≦x≦4$のとき、$y$の変域を求めなさい。
この動画を見る
①$y$は$x$に比例し、$x = 3$のとき$y=6$である。
また、$x$の変域が$-4≦ x \leqq 3$のとき、その変域は$a\leqq y\leqq b$である。
$a、b$の値を求めよ。
②$y$は$x$に比例し、$ x = 2$ のとき$y=-5$である。
また、$x$の変域が$-6≦x≦-4$のとき、 $y$の変域を求めなさい。
③$y$は$x$に反比例し、$x=-4$のとき$y=-6$である。
また、$x$の変域が$2≦x≦4$のとき、$y$の変域を求めなさい。
【テスト対策 中1】4章-3
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
変数$x$のとる値が次の場合に、$x$の変域を不等号を使って表しなさい。
①$-2$より大きく$5$以下
②$-4$以上$7$未満
③$3$より小さい
④$-8$以上
⑤$2$より$7$より小さい
⑥$-1$未満
この動画を見る
変数$x$のとる値が次の場合に、$x$の変域を不等号を使って表しなさい。
①$-2$より大きく$5$以下
②$-4$以上$7$未満
③$3$より小さい
④$-8$以上
⑤$2$より$7$より小さい
⑥$-1$未満
【テスト対策 中1】4章-1
単元：
#数学(中学生)#中１数学#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の2つの数量$x,y$について、$y$が$x$に比例するものには○、反比例するものには△、
どちらでもないものには×をつけなさい。
また、○と△については、$x,y$の関係を式に表しなさい。
①1本$x$円のジュース8本の代金$y$円
②時速50kmの速さで走る自動車は、$x$時間に$y$km進む
③身長$xcm$の人の体重は$y$kgである
④30km離れた場所に、時速$xkm$の自転車で行くと$y$時間かかる
⑤半径$xcm$の円の面積は$ycm$である
⑥120個のアメを$x$人に同じ数で分けると、1人分は$y$個である
この動画を見る
次の2つの数量$x,y$について、$y$が$x$に比例するものには○、反比例するものには△、
どちらでもないものには×をつけなさい。
また、○と△については、$x,y$の関係を式に表しなさい。
①1本$x$円のジュース8本の代金$y$円
②時速50kmの速さで走る自動車は、$x$時間に$y$km進む
③身長$xcm$の人の体重は$y$kgである
④30km離れた場所に、時速$xkm$の自転車で行くと$y$時間かかる
⑤半径$xcm$の円の面積は$ycm$である
⑥120個のアメを$x$人に同じ数で分けると、1人分は$y$個である
【テスト対策 中2】4章-6
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
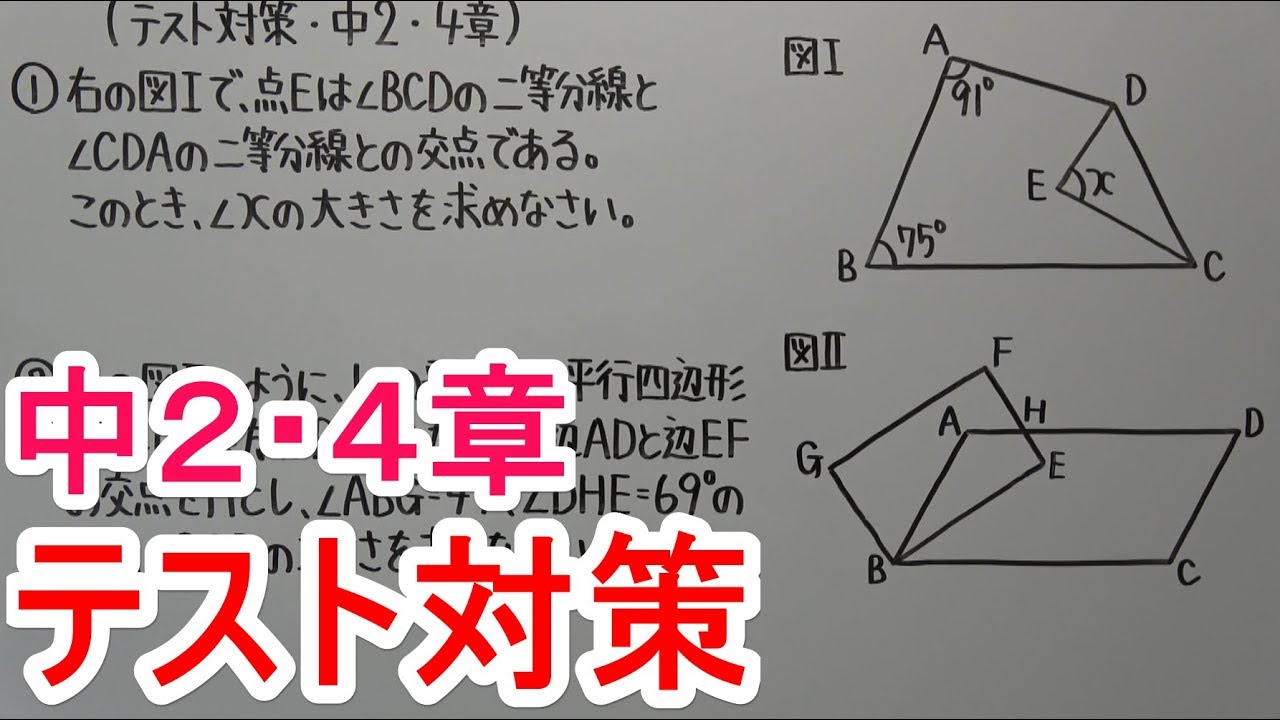
①右の図Iで、点$E$は$∠BCD$の二等分線と$∠CDA$の二等分線との交点である。
このとき、$∠X$の大きさを求めなさい。
② 右の図Ⅱのように、1つの平面上に平行四辺形$ABCD$と長方形$BEFG$がある。
辺$AD$と辺$EF$ の交点を$H$とし、$\angle ABG = 49°、\angle DHE = 69°$のとき、
$∠BCD$の大きさを求めなさい。
図は動画内参照
この動画を見る
①右の図Iで、点$E$は$∠BCD$の二等分線と$∠CDA$の二等分線との交点である。
このとき、$∠X$の大きさを求めなさい。
② 右の図Ⅱのように、1つの平面上に平行四辺形$ABCD$と長方形$BEFG$がある。
辺$AD$と辺$EF$ の交点を$H$とし、$\angle ABG = 49°、\angle DHE = 69°$のとき、
$∠BCD$の大きさを求めなさい。
図は動画内参照
【テスト対策 中2】4章-5
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
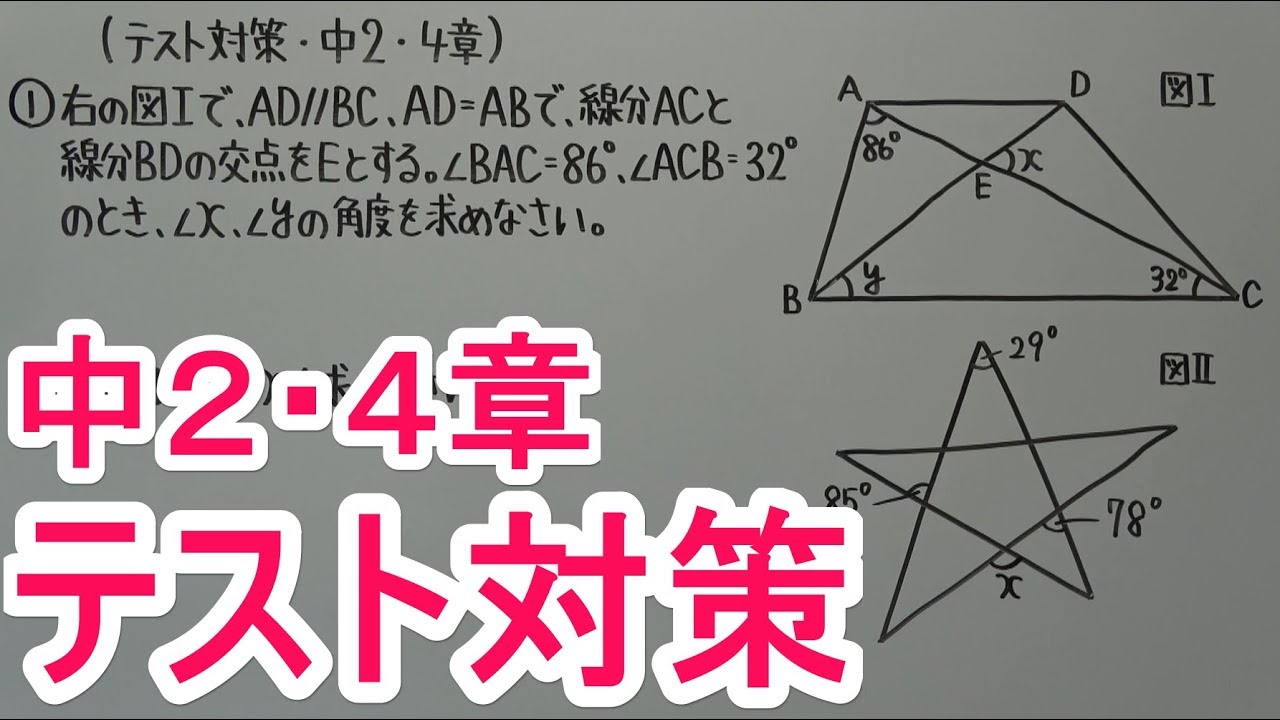
右の図Iで、$AD /\!/ BC,AD=AB$で、線分$AC$と線分$BD$の交点を$E$とする。
$\angle BAC=86°、\angle ACB=32°$のとき、
$\angle x,\angle y$の角度を求めなさい。
②右の図IIで、$\angle x$を求めなさい。
図は動画内参照
この動画を見る
右の図Iで、$AD /\!/ BC,AD=AB$で、線分$AC$と線分$BD$の交点を$E$とする。
$\angle BAC=86°、\angle ACB=32°$のとき、
$\angle x,\angle y$の角度を求めなさい。
②右の図IIで、$\angle x$を求めなさい。
図は動画内参照
【テスト対策 中2】4章-4
単元：
#数学(中学生)#中１数学#角度と面積#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のような図形について、次の各問に答えなさい。
①$\angle a+\angle b+\angle c+\angle d+\angle e$を求めなさい。
② ①を証明しなさい。ただし、解答欄の図に頂点や角度を
書き込んでよいものとする。(例：頂点$F,\angle F$)$
図は動画内参照
この動画を見る
右の図のような図形について、次の各問に答えなさい。
①$\angle a+\angle b+\angle c+\angle d+\angle e$を求めなさい。
② ①を証明しなさい。ただし、解答欄の図に頂点や角度を
書き込んでよいものとする。(例：頂点$F,\angle F$)$
図は動画内参照
【テスト対策 中2】4章-3
単元：
#数学(中学生)#中２数学#角度と面積#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
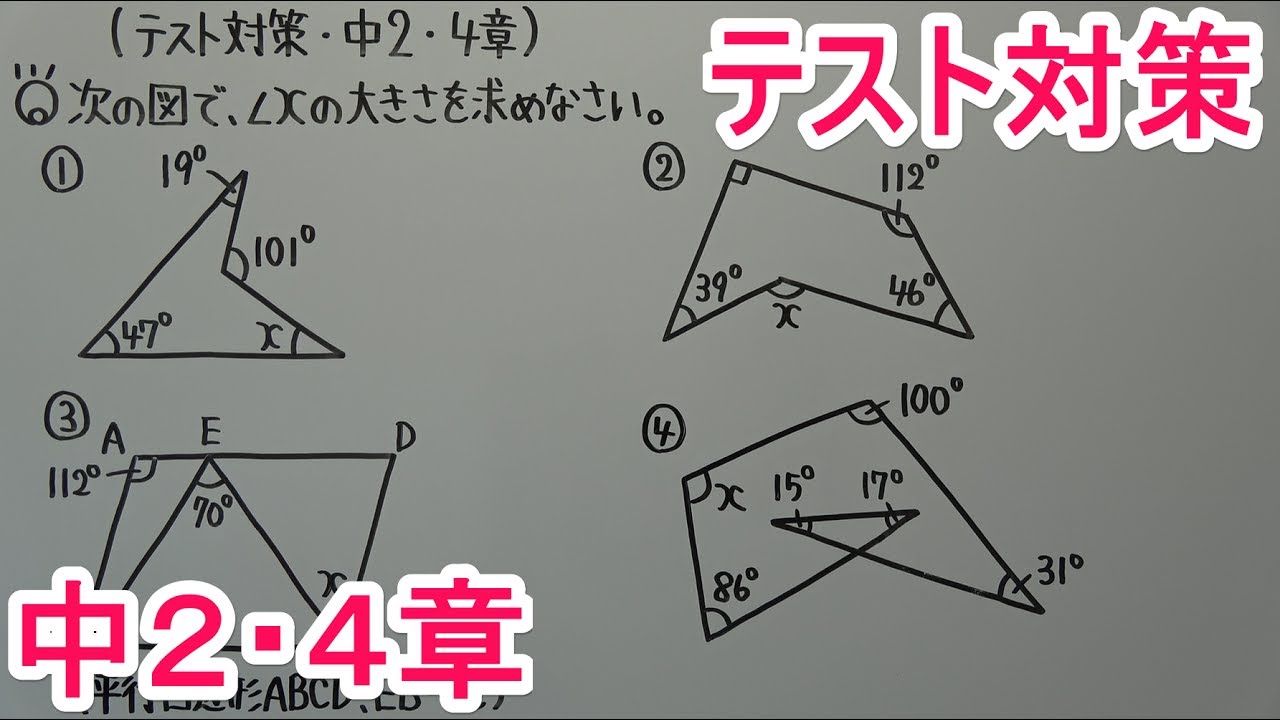
次の図①～④で、$\angle x$の大きさを求めなさい。
図は動画内参照
この動画を見る
次の図①～④で、$\angle x$の大きさを求めなさい。
図は動画内参照
【テスト対策 中2】4章-2
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図形について$\Box$にあてはまる式や数を書きなさい。
1つの頂点から、ほかの各頂点に対角線を引くと①個の三角形に分けられるので、
内角の和は②で計算できる。
③十二角形の内角の和を求めなさい。
④正九角形の1つの内角の大きさを求めなさい。
⑤正二十角形の1つの外角の大きさを求めなさい。
図は動画内参照
この動画を見る
右の図形について$\Box$にあてはまる式や数を書きなさい。
1つの頂点から、ほかの各頂点に対角線を引くと①個の三角形に分けられるので、
内角の和は②で計算できる。
③十二角形の内角の和を求めなさい。
④正九角形の1つの内角の大きさを求めなさい。
⑤正二十角形の1つの外角の大きさを求めなさい。
図は動画内参照
【テスト対策・中２】４章－１
単元：
#数学(中学生)#中２数学#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
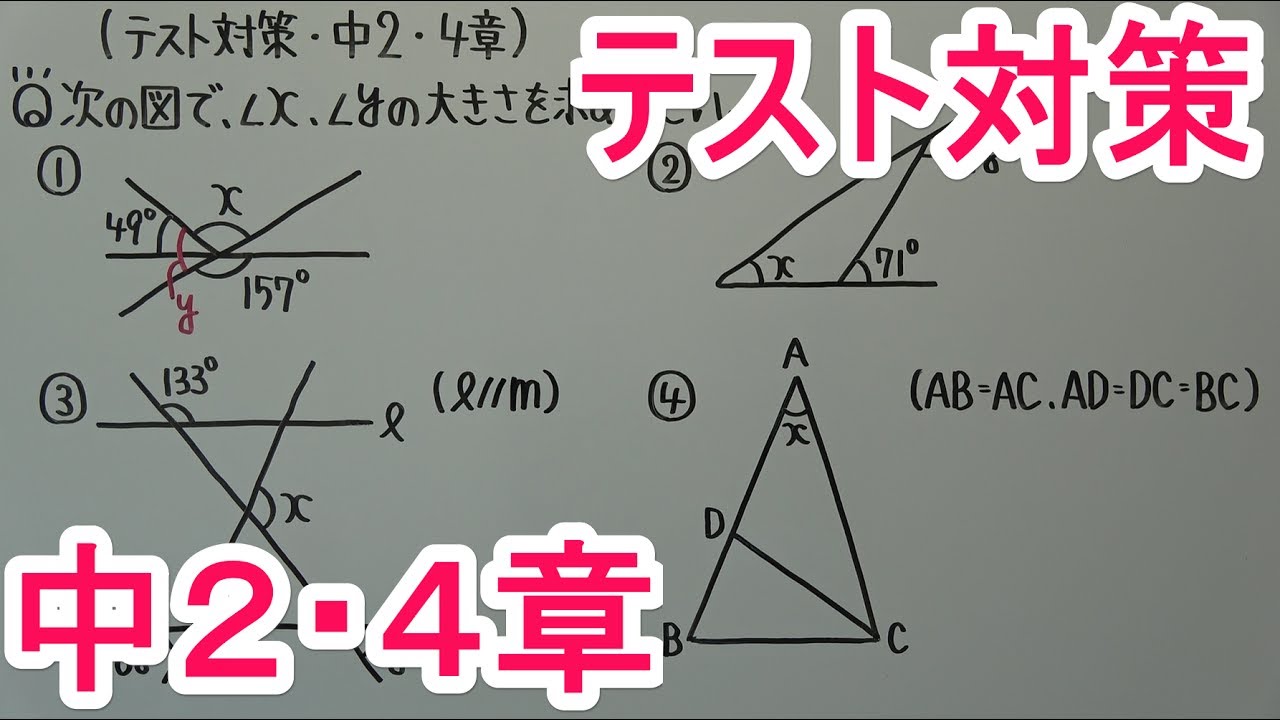
次の図①～④で、$\angle x,\angle y$の大きさを求めなさい。
図は動画内参照
この動画を見る
次の図①～④で、$\angle x,\angle y$の大きさを求めなさい。
図は動画内参照