 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
equation : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-4x=(x-\fbox{①})^2-\fbox②$という等式が成り立つように、①、②に当てはまる数を求めよ。
この動画を見る
$x^2-4x=(x-\fbox{①})^2-\fbox②$という等式が成り立つように、①、②に当てはまる数を求めよ。
よくある円のパターン 〇〇をみつけろ! 灘高校
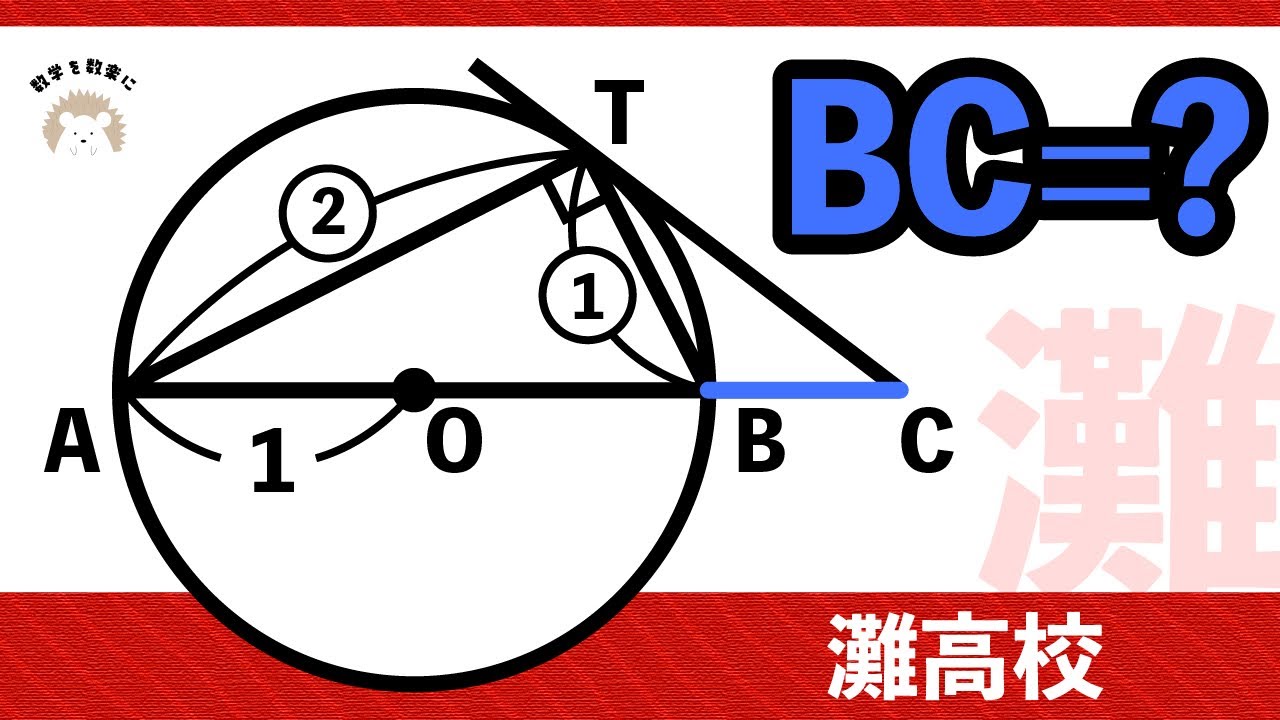
よくある円のパターン 〇〇をみつけろ! 灘高校

よくある円のパターン 〇〇をみつけろ! 灘高校

文字式の値を求める方法はいくつかある!~全国入試問題解法 #数学 #高校入試#数検 #mathematics #名言 #勉強
単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
等式$\frac{1}{x}-\frac{2}{y}=3$が成り立つとき、$\frac{6x-3y}{3xy-2x+y}$の値を求めなさい。
この動画を見る
等式$\frac{1}{x}-\frac{2}{y}=3$が成り立つとき、$\frac{6x-3y}{3xy-2x+y}$の値を求めなさい。
4つの正方形
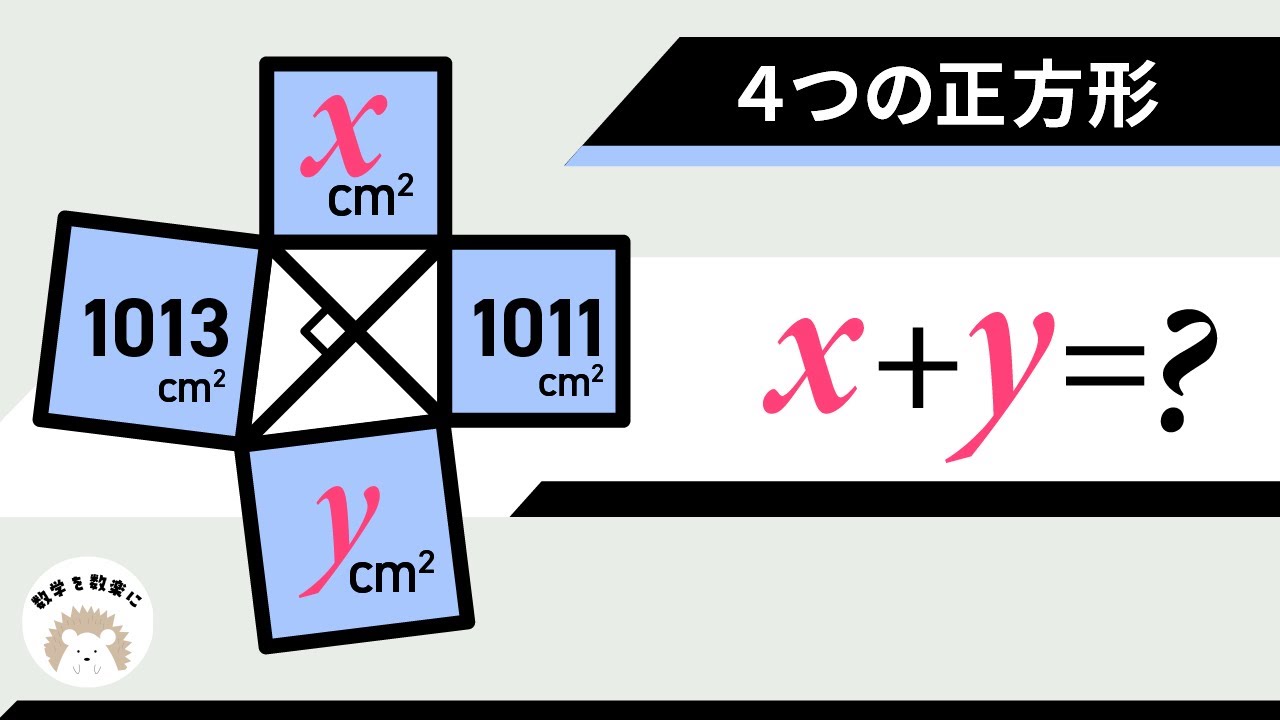
4つの正方形

4つの正方形

【同じ直線上だから…!】一次関数:法政大学高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3点$A(-4,13),B(1,3),C(5,a)$が同じ直線上にある時、定数$a$の値を求めなさい。
この動画を見る
3点$A(-4,13),B(1,3),C(5,a)$が同じ直線上にある時、定数$a$の値を求めなさい。
式の値

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c=0$のとき
$\displaystyle \frac{a+b}{c}+\frac{b+c}{a}+\frac{a+c}{b}=$
この動画を見る
$a+b+c=0$のとき
$\displaystyle \frac{a+b}{c}+\frac{b+c}{a}+\frac{a+c}{b}=$
気づいた?
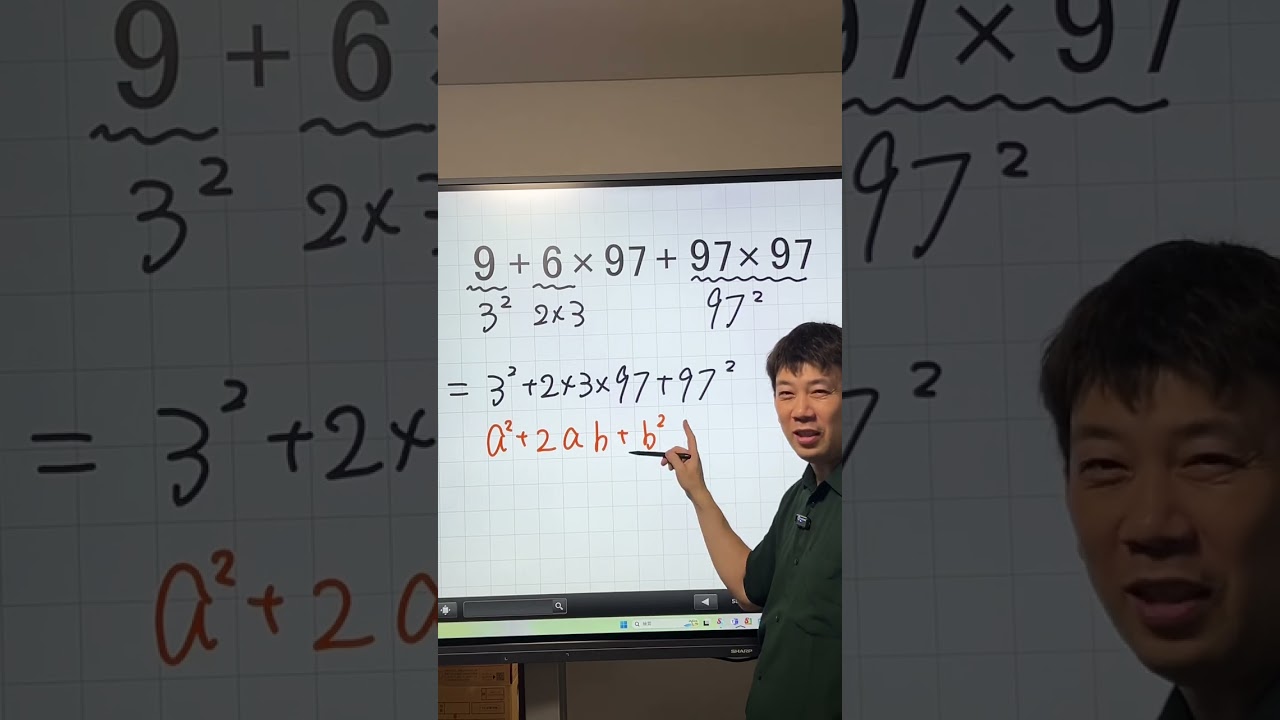
気づいた?
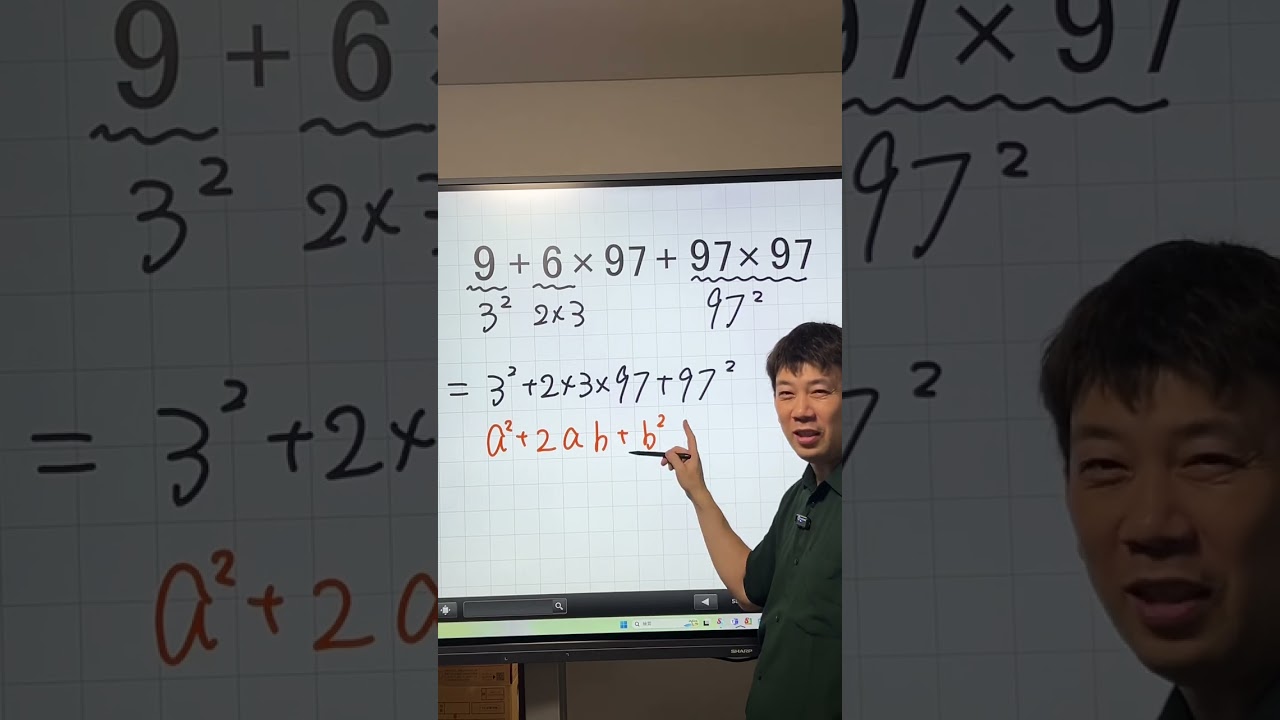
正方形の折り返し 大分東明
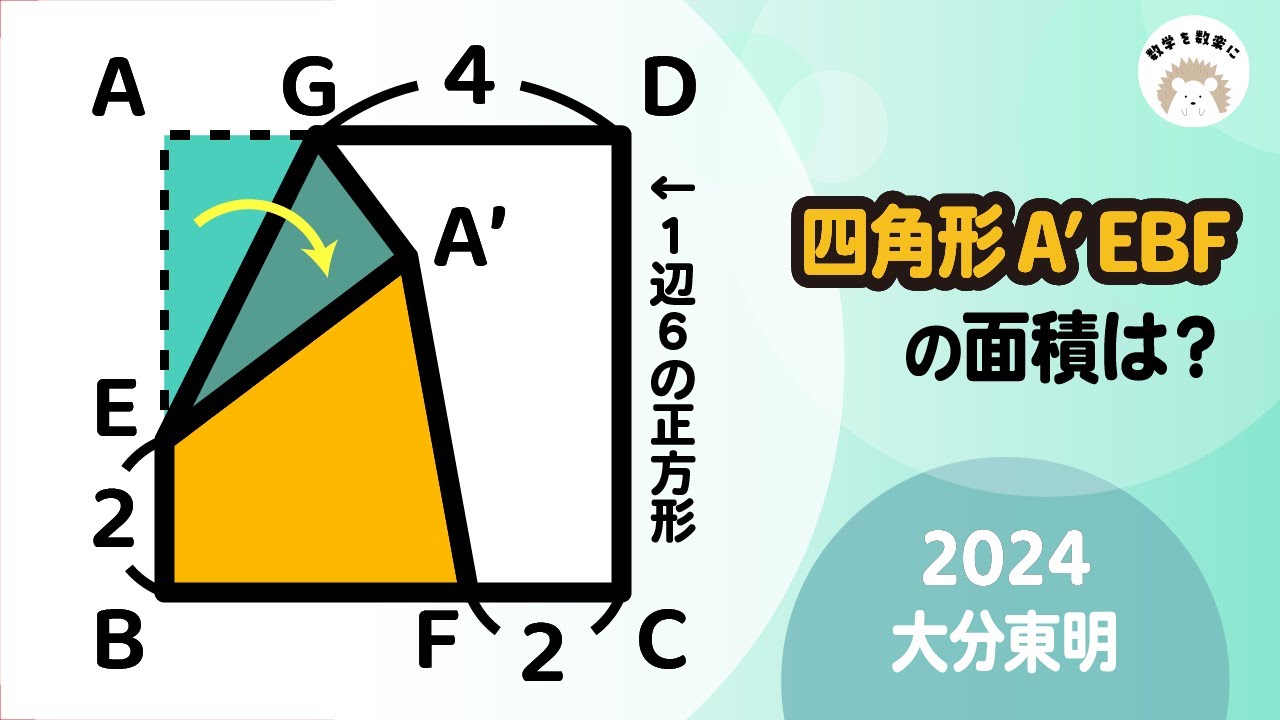
正方形の折り返し 大分東明

【大学入試同然…!?】確率:須磨学園高等学校~全国入試問題解法【大学入試同然…!?】確率:須磨学園高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
太郎君はAを出発しBへ一定の速さで移動する。次郎君は太郎君が出発するのと同時に、Bを出発しAへ太郎君と同じ速さで移動する。太郎君と次郎君が交差点上で出会わない確率を求めなさい。
この動画を見る
太郎君はAを出発しBへ一定の速さで移動する。次郎君は太郎君が出発するのと同時に、Bを出発しAへ太郎君と同じ速さで移動する。太郎君と次郎君が交差点上で出会わない確率を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 折り返した図形2

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
この動画を見る
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
代入法どっちにいれてええん?

【順に考えて…!】整数:東海高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東海高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{171+b^2}$の値が整数となるような自然数$b$をすべて求めよ。
この動画を見る
$\sqrt{171+b^2}$の値が整数となるような自然数$b$をすべて求めよ。
2024 渋谷幕張 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を因数分解せよ。
$x^3-xy^2+2xy-x^2+y^2-x-2y+1$
出典:2024渋谷教育学園幕張中学校
この動画を見る
以下を因数分解せよ。
$x^3-xy^2+2xy-x^2+y^2-x-2y+1$
出典:2024渋谷教育学園幕張中学校
【そのまま足したり引いたり…!?】整数:鹿屋中央高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#鹿屋中央高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 鹿屋中央高等学校
次の問いに答えよ
$\sqrt{ 2 }+\sqrt{ n }=\sqrt{ 18 }$
を満たす自然数を求めよ。
この動画を見る
入試問題 鹿屋中央高等学校
次の問いに答えよ
$\sqrt{ 2 }+\sqrt{ n }=\sqrt{ 18 }$
を満たす自然数を求めよ。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 折り返した図形1

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、円A,B,Cは縦4cm,横6cmの長方形の辺に接し、円AとCおよび円BとCはそれぞれ外接している。円A,Bの半径がともに1cmであるとき、円Cの半径を求めなさい。
この動画を見る
右の図のように、円A,B,Cは縦4cm,横6cmの長方形の辺に接し、円AとCおよび円BとCはそれぞれ外接している。円A,Bの半径がともに1cmであるとき、円Cの半径を求めなさい。
難解な角度を求める問題
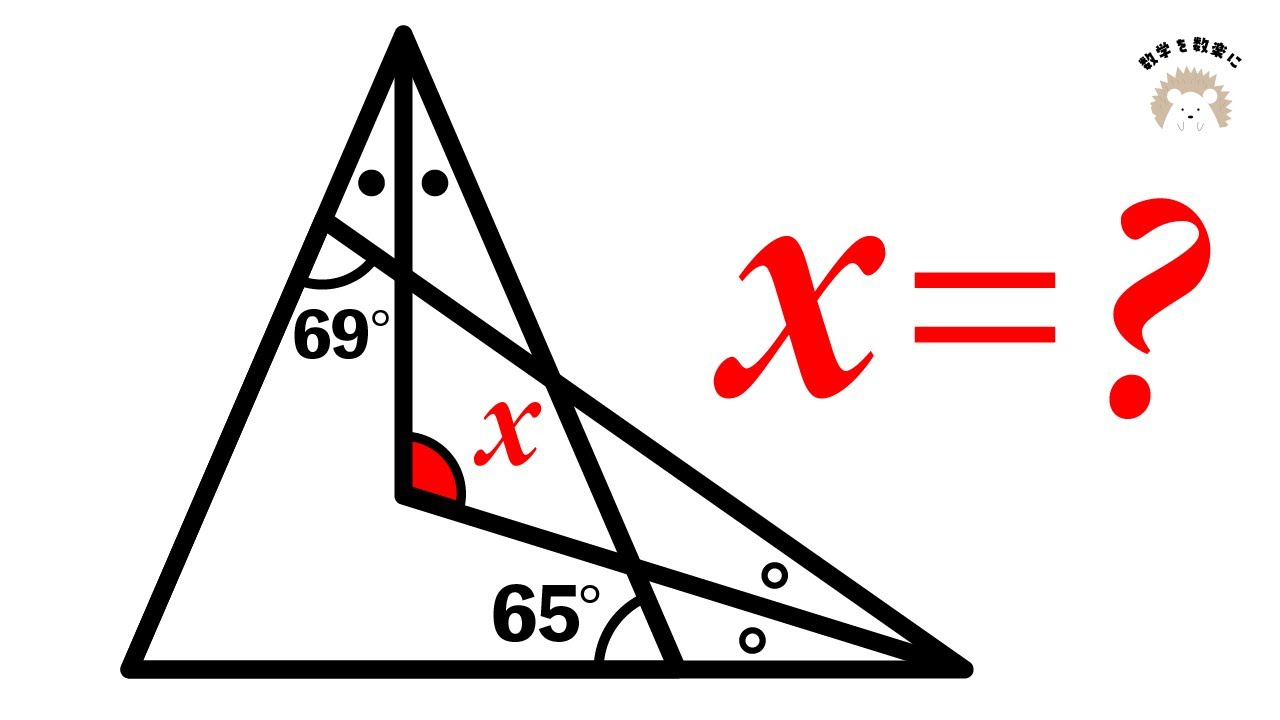
【上手いやり方は…!】文字式:巣鴨高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#巣鴨高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 巣鴨高等学校
$0$でない数$x,y,z$が
次の2つの方程式を 満たすとき・・・
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - 2y - z = 0 \\
2x + y + z = 0
\end{array}
\right.
\end{eqnarray}$
$\displaystyle \frac{x^3+y^3+z^3}{xyz}$の値を求めよ。
この動画を見る
入試問題 巣鴨高等学校
$0$でない数$x,y,z$が
次の2つの方程式を 満たすとき・・・
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - 2y - z = 0 \\
2x + y + z = 0
\end{array}
\right.
\end{eqnarray}$
$\displaystyle \frac{x^3+y^3+z^3}{xyz}$の値を求めよ。
【分析せよ…!】整数:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 和洋国府台女子高等学校
$980$にできるだけ
小さな自然数Nをかけて、
ある自然数の$3$乗にしたい。
このとき・・・
$N$の値を求めよ。
この動画を見る
入試問題 和洋国府台女子高等学校
$980$にできるだけ
小さな自然数Nをかけて、
ある自然数の$3$乗にしたい。
このとき・・・
$N$の値を求めよ。
square root : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
square root : Shirotan's cute kawaii math show
$\displaystyle \frac{(\sqrt{ 14 }-\sqrt{ 6 })(\sqrt{ 7}+\sqrt{ 3 } )}{2}-(\sqrt{ 2 }+1)^2=?$
を計算せよ。
この動画を見る
square root : Shirotan's cute kawaii math show
$\displaystyle \frac{(\sqrt{ 14 }-\sqrt{ 6 })(\sqrt{ 7}+\sqrt{ 3 } )}{2}-(\sqrt{ 2 }+1)^2=?$
を計算せよ。
福田のおもしろ数学181〜連続する4つの自然数の積は平方数にならないことの証明

食塩水 2024神奈川県

単元:
#数学(中学生)#中1数学#方程式#高校入試過去問(数学)#神奈川県公立高校入試#神奈川県公立高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
4%の食塩水300gが入ったビーカーから食塩水$a$gを取り出した。
その後ビーカーに残っている食塩水に食塩$a$gを加えてよくかき混ぜたところ12%の食塩水になった。
$a$を求めよ。
この動画を見る
4%の食塩水300gが入ったビーカーから食塩水$a$gを取り出した。
その後ビーカーに残っている食塩水に食塩$a$gを加えてよくかき混ぜたところ12%の食塩水になった。
$a$を求めよ。
連立方程式は基礎が大切!~全国入試問題解法 #数学 #数検 #高校入試 #名言 #連立方程式
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式は基礎が大切!~全国入試問題解法
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 3y = 1 \\
8x + 9y = 7
\end{array}
\right.
\end{eqnarray}$
この動画を見る
連立方程式は基礎が大切!~全国入試問題解法
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 3y = 1 \\
8x + 9y = 7
\end{array}
\right.
\end{eqnarray}$
X=2 堀川高校

単元:
#数学(中学生)#中2数学#中3数学#2次方程式#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
この動画を見る
$x=2$が解の1つであるものをすべて選べ
$2x^2+8x-8=0$
$x^3-3x^2+5x-6=0$
$6 \leqq 3x \leqq x+4$
$1+\displaystyle \frac{1}{x}+\displaystyle \frac{1}{x^2}+\displaystyle \frac{1}{x^3} \lt 2$
【小数を含むところが…!】整数:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
$\sqrt{ 0.48n }$が整数と
なるような 自然数$n$のうち・・・
最も小さいものを求めよ。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
$\sqrt{ 0.48n }$が整数と
なるような 自然数$n$のうち・・・
最も小さいものを求めよ。
