数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
4人でじゃんけんの確率✊✌️✋ 鹿児島実業

7で割ったあまり 札幌大谷

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
この動画を見る
$10^{2021}$を7で割った余りは?
札幌大谷高等学校(改)
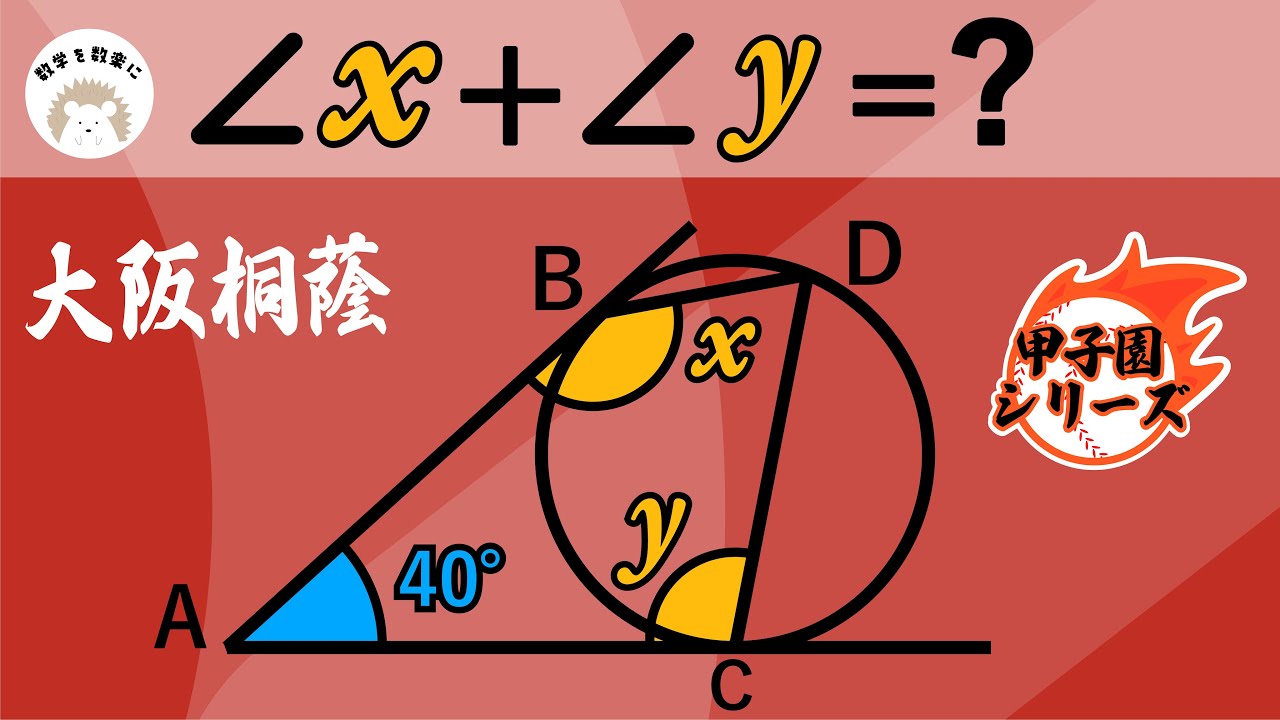
円 角の和 大阪桐蔭
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x +\angle y = ?$
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
$\angle x +\angle y = ?$
*図は動画内参照
大阪桐蔭高等学校
変形できるかできないかが分かれ目 聖望学園

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{6 \sqrt n}{n}$が自然数となる自然数nは何個?
聖望学園高等学校
この動画を見る
$\frac{6 \sqrt n}{n}$が自然数となる自然数nは何個?
聖望学園高等学校
【中学数学】四則演算の宿題Live【中1夏期講習①】

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(1)\,3\times (-2)\div (-7)\times \{ -4\times (-4)\}$
$(2)\,\displaystyle \frac{3}{2}\div \left(-\frac{2}{7}\right)\div \left(-\frac{4}{7}\right)$
$(3)\,\displaystyle \left\{ 5\div \left( -\frac{2}{5}\div 3\right)\times \frac{2}{3}\right\}\times \left( -\frac{1}{2}\right)$
$(4)\,6^3\div (-3)^3+2^2\times (-3)$
$(5)\,(2+5)\times 4+\{3+(2-6)\times 4\}$
$(6)\,\{3^2-(-4)^2\}-(2^3-7)\times 6$
$(7)\,\displaystyle \frac{6}{5} \times \left(-\frac{5}{4}\right)-\left(-\frac{9}{8}\right)\div \frac{3}{10}$
$\displaystyle(8)\, \left\{ \left( \frac{5}{4}-\frac{11}{2}\right)\div\frac{2}{3}+\frac{1}{4}\right\}-\frac{5}{24}$
$\displaystyle (9)\, -7 \div \left(-\frac{1}{2}\right)-(-7)-\left\{-\frac{1}{3}+(-4)\right\}$
$\displaystyle (10)\, \frac{4}{3} \times \left\{-\frac{1}{4} - \left(-\frac{1}{6}\right) \right\} - \left(-\frac{11}{6} \right) \div \frac{11}{4}$
この動画を見る
$(1)\,3\times (-2)\div (-7)\times \{ -4\times (-4)\}$
$(2)\,\displaystyle \frac{3}{2}\div \left(-\frac{2}{7}\right)\div \left(-\frac{4}{7}\right)$
$(3)\,\displaystyle \left\{ 5\div \left( -\frac{2}{5}\div 3\right)\times \frac{2}{3}\right\}\times \left( -\frac{1}{2}\right)$
$(4)\,6^3\div (-3)^3+2^2\times (-3)$
$(5)\,(2+5)\times 4+\{3+(2-6)\times 4\}$
$(6)\,\{3^2-(-4)^2\}-(2^3-7)\times 6$
$(7)\,\displaystyle \frac{6}{5} \times \left(-\frac{5}{4}\right)-\left(-\frac{9}{8}\right)\div \frac{3}{10}$
$\displaystyle(8)\, \left\{ \left( \frac{5}{4}-\frac{11}{2}\right)\div\frac{2}{3}+\frac{1}{4}\right\}-\frac{5}{24}$
$\displaystyle (9)\, -7 \div \left(-\frac{1}{2}\right)-(-7)-\left\{-\frac{1}{3}+(-4)\right\}$
$\displaystyle (10)\, \frac{4}{3} \times \left\{-\frac{1}{4} - \left(-\frac{1}{6}\right) \right\} - \left(-\frac{11}{6} \right) \div \frac{11}{4}$
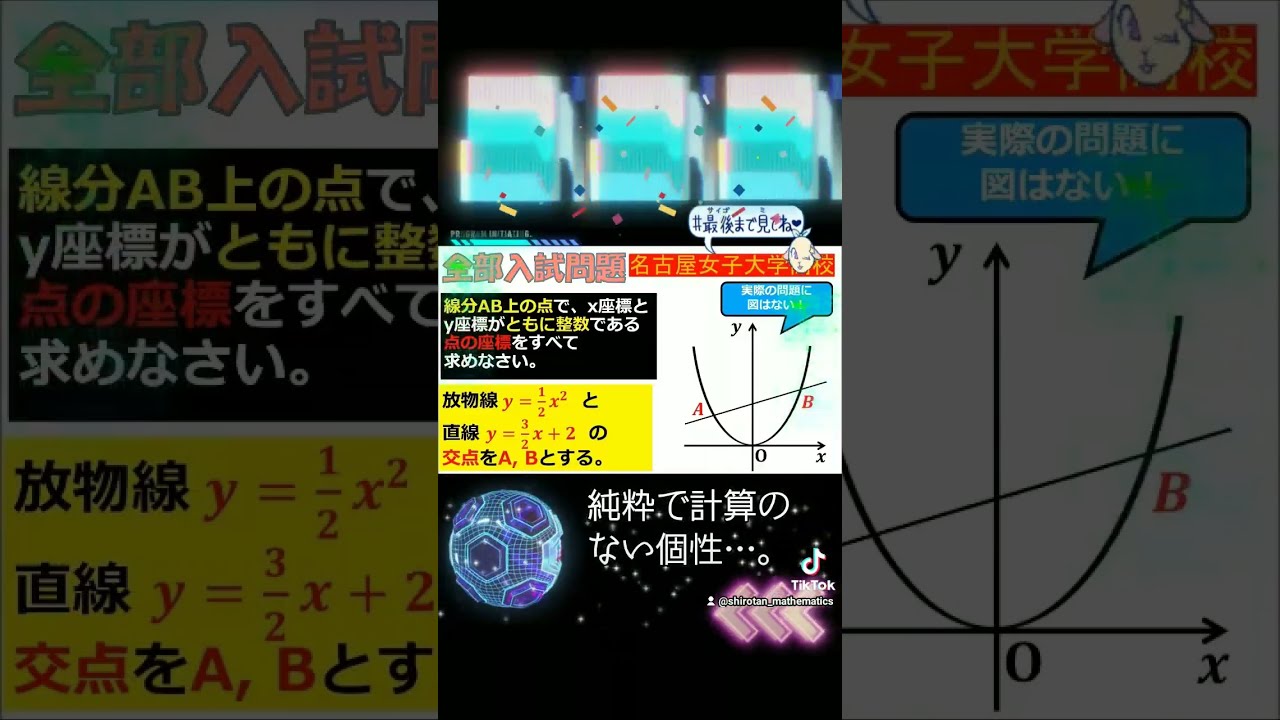
中学から高校での数学の要点を30秒にまとめた動画~全国入試問題解法 #Shorts #夏休み #高校受験
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
交点を$A,B$とする.
線分$AB$上の点で$x$座標と$y$座標が共に整数である.
$ y=\dfrac{1}{2}x^2$
$ y=\dfrac{3}{2}x+2$
すべて求めよ.
この動画を見る
交点を$A,B$とする.
線分$AB$上の点で$x$座標と$y$座標が共に整数である.
$ y=\dfrac{1}{2}x^2$
$ y=\dfrac{3}{2}x+2$
すべて求めよ.
久しぶりにあの条件発動 札幌大谷
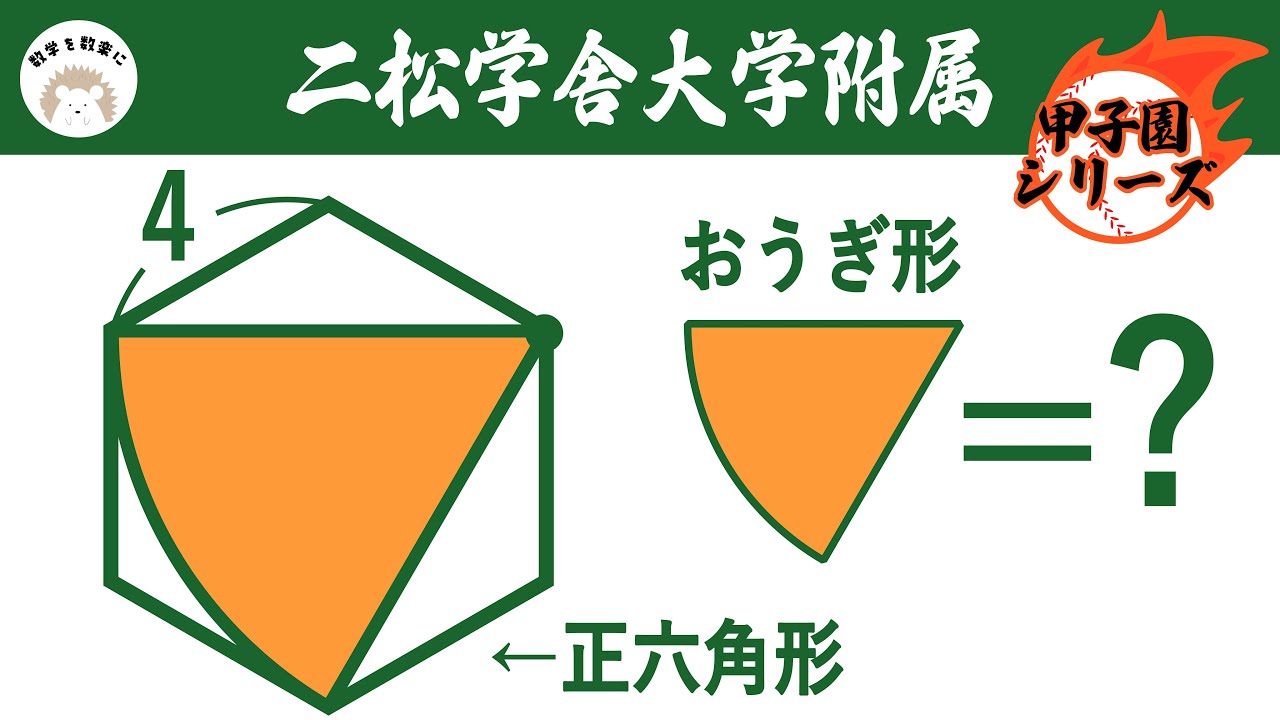
正六角形の中のおうぎ形 二松学舎大附属
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
おうぎ形の面積=?
*図は動画内参照
二松学舎大学附属高等学校
この動画を見る
おうぎ形の面積=?
*図は動画内参照
二松学舎大学附属高等学校
ルートが入ってる方程式 日大三

単元:
#数学(中学生)#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$\sqrt 2 x = \frac{1}{\sqrt 2} - \frac{1}{\sqrt 3}$
日本大学第三高等学校
この動画を見る
方程式を解け
$\sqrt 2 x = \frac{1}{\sqrt 2} - \frac{1}{\sqrt 3}$
日本大学第三高等学校
気づけるか? 三重高校
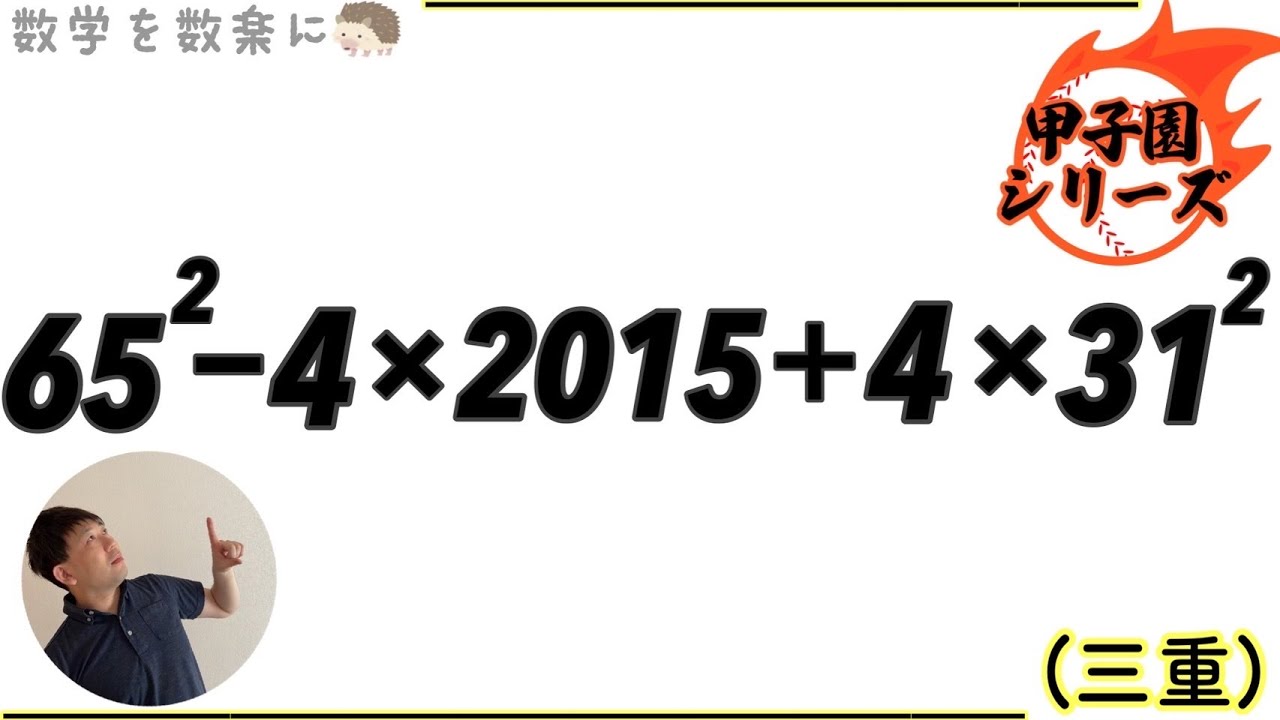
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$65^2-4 \times 2015 + 4 \times 31^2$
三重高等学校
この動画を見る
$65^2-4 \times 2015 + 4 \times 31^2$
三重高等学校
式の値 日大三
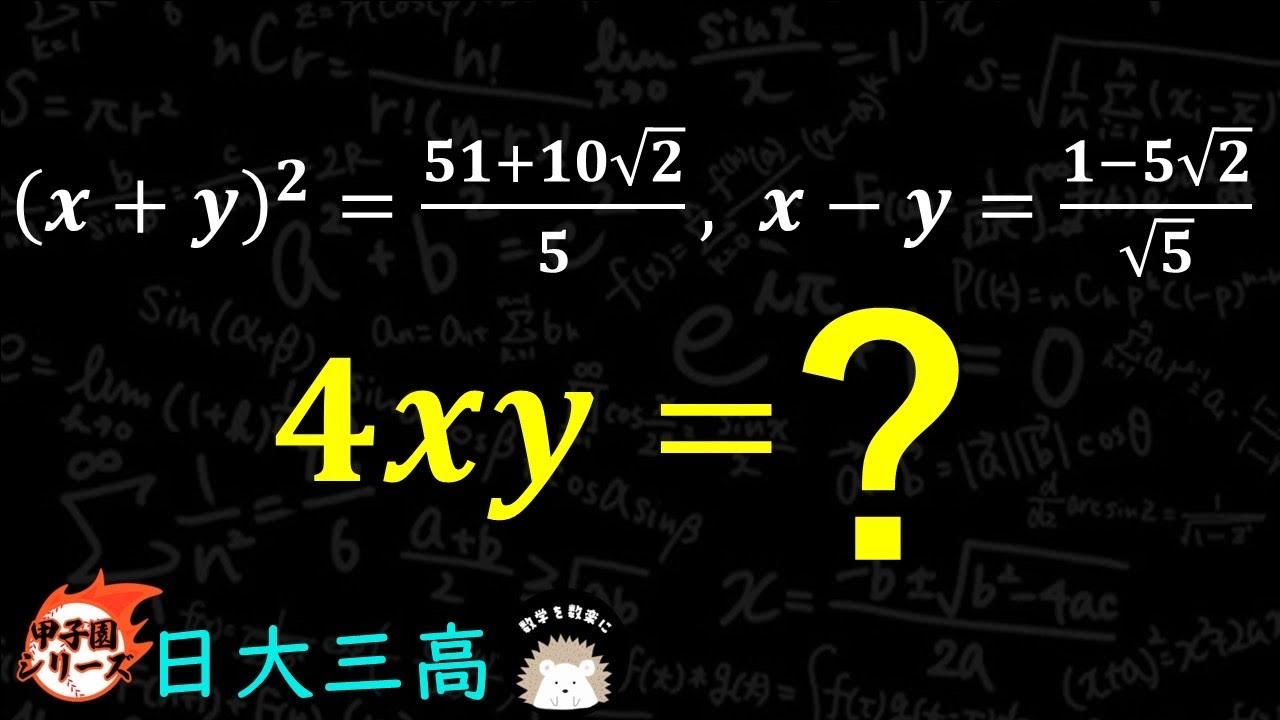
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+y)^2 = \frac{51 + 10 \sqrt 2}{5}$ , $x-y = \frac{1-5 \sqrt 2}{\sqrt 5}$
$4xy=?$
日本大学第三高等学校
この動画を見る
$(x+y)^2 = \frac{51 + 10 \sqrt 2}{5}$ , $x-y = \frac{1-5 \sqrt 2}{\sqrt 5}$
$4xy=?$
日本大学第三高等学校
【中学数学】連立方程式の計算問題~標準レベル~【中2夏期講習②】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle (1)\, \begin{cases}
3\times(x+y-1)-4y=5 \\
5x-3(2x-y-3)=17
\end{cases}
$
$\displaystyle (2)\, \begin{cases}
0.06x+0.04y=16 \\
x+y=300
\end{cases}
$
$\displaystyle (3)\, \begin{cases}
0.2x-0.3y=0.7\\
\frac{1}{4}x+\frac{1}{3}y=\frac{1}{6}
\end{cases}
$
$\displaystyle (4)\,
5x-4y-15=3x+2y-11=-2
$
$\displaystyle (5)\,\begin{cases}
-6ax + 5by = 9\\
4bx + 3ay = 26
\end{cases}の解がx=2, \,y=3のとき、a,bを求めよ。
$
この動画を見る
$\displaystyle (1)\, \begin{cases}
3\times(x+y-1)-4y=5 \\
5x-3(2x-y-3)=17
\end{cases}
$
$\displaystyle (2)\, \begin{cases}
0.06x+0.04y=16 \\
x+y=300
\end{cases}
$
$\displaystyle (3)\, \begin{cases}
0.2x-0.3y=0.7\\
\frac{1}{4}x+\frac{1}{3}y=\frac{1}{6}
\end{cases}
$
$\displaystyle (4)\,
5x-4y-15=3x+2y-11=-2
$
$\displaystyle (5)\,\begin{cases}
-6ax + 5by = 9\\
4bx + 3ay = 26
\end{cases}の解がx=2, \,y=3のとき、a,bを求めよ。
$
普通の中学生が解くには難しい 興南高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
5つの数字0,1,2,6,7から異なる3つの数字を選び、並べて3ケタの数を作とき
5で割ると2余る数は何個できるか?
興南高等学校
この動画を見る
5つの数字0,1,2,6,7から異なる3つの数字を選び、並べて3ケタの数を作とき
5で割ると2余る数は何個できるか?
興南高等学校
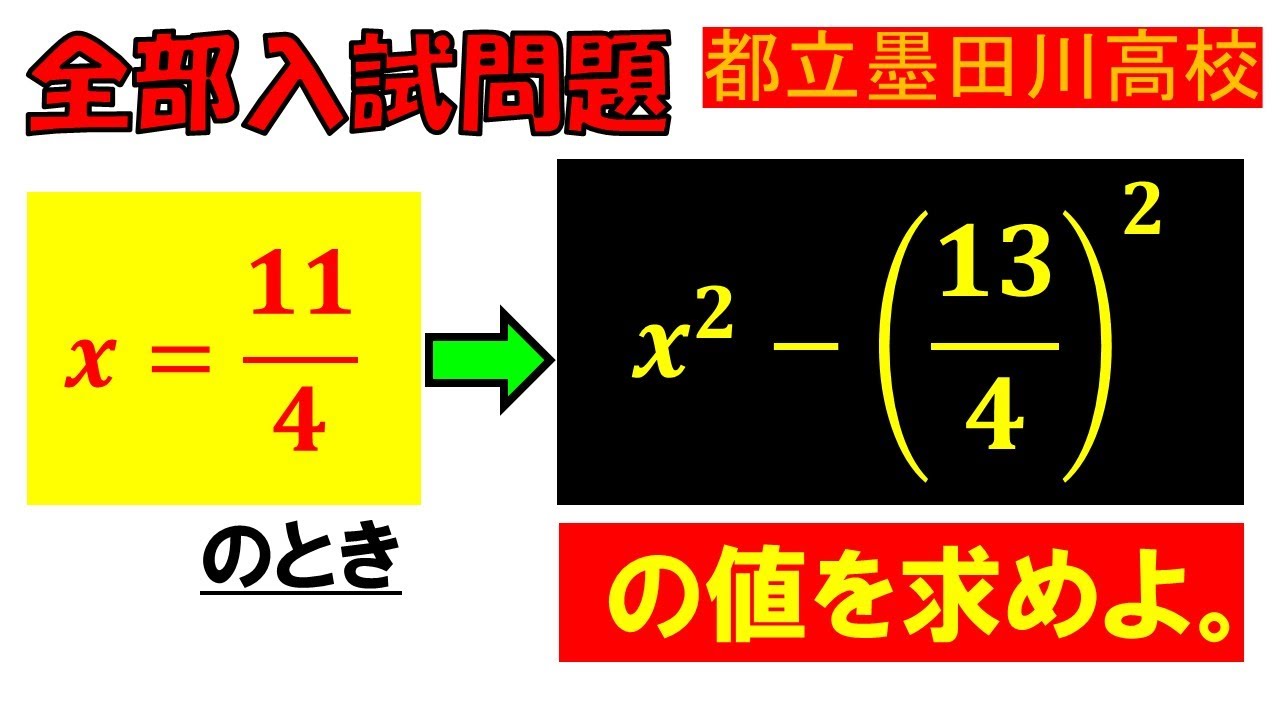
【まずは3分で理解!それだけじゃなく…】文字式:東京都立墨田川高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=\dfrac{11}{4}$のとき,$ x^2- \left(\dfrac{13}{4}\right)^2$の値を求めよ.
東京都立墨田川高等学校過去問
この動画を見る
$ x=\dfrac{11}{4}$のとき,$ x^2- \left(\dfrac{13}{4}\right)^2$の値を求めよ.
東京都立墨田川高等学校過去問
二次関数の変域 天理高校

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=x^2$
xの変域が$a \leqq x \leqq 2$のとき
yの変域が$0 \leqq y \leqq 4$となる
aの値の範囲は?
天理高等学校
この動画を見る
$y=x^2$
xの変域が$a \leqq x \leqq 2$のとき
yの変域が$0 \leqq y \leqq 4$となる
aの値の範囲は?
天理高等学校
中学生の解き方 高校生の解き方 日本文理
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
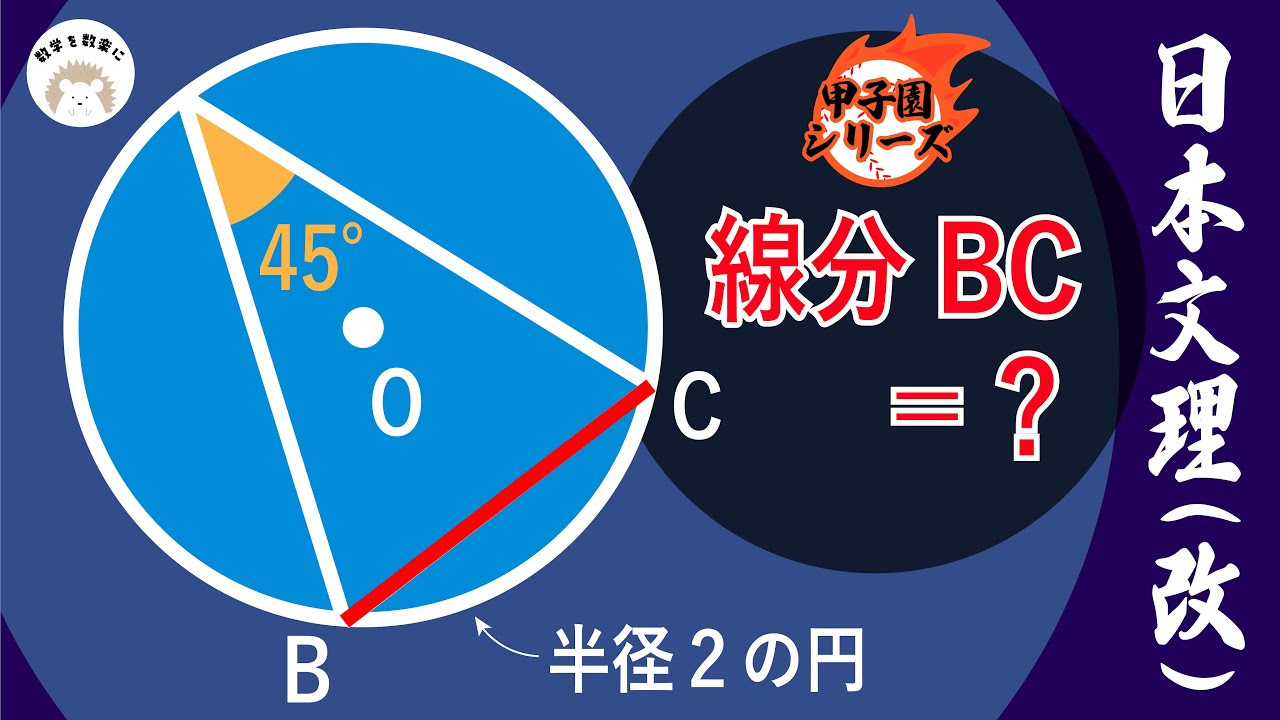
円の半径=2
線分BC=?
*図は動画内参照
日本文理高等学校(改)
この動画を見る
円の半径=2
線分BC=?
*図は動画内参照
日本文理高等学校(改)
整数問題 海星高校(長崎)
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
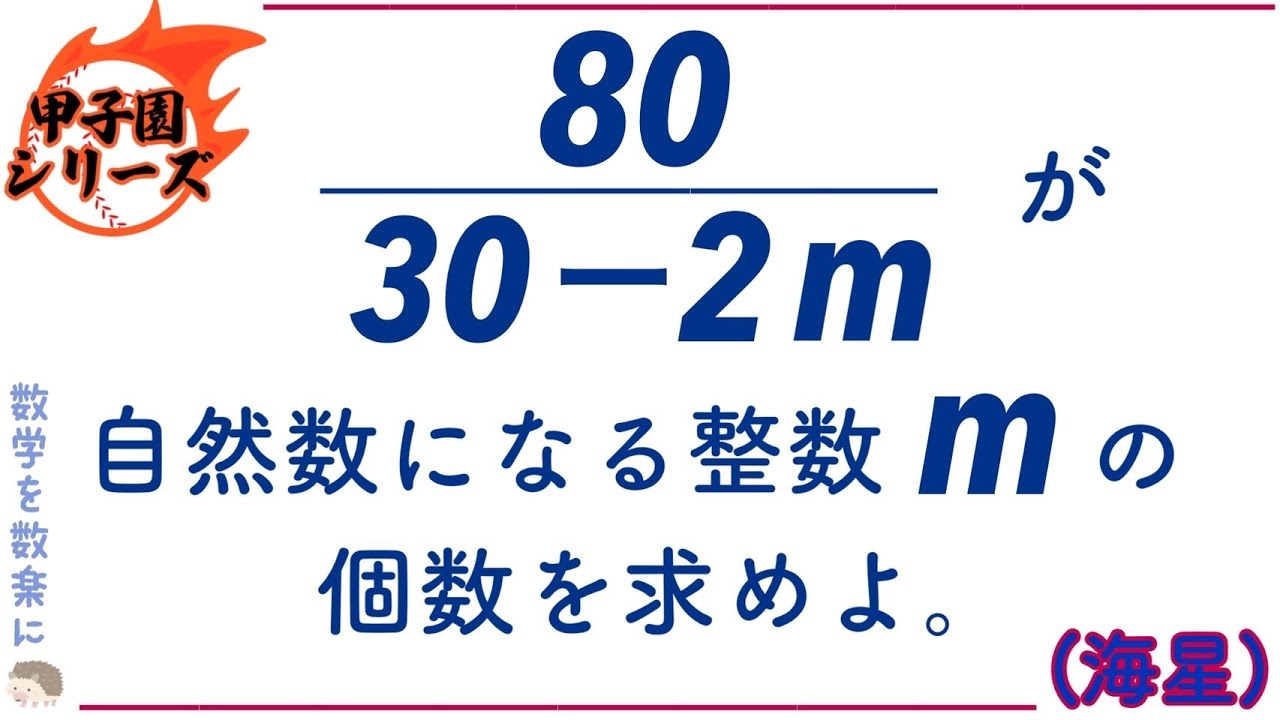
$\frac{80}{30 - 2m}$が自然数になる整数mの個数を求めよ。
海星高校
この動画を見る
$\frac{80}{30 - 2m}$が自然数になる整数mの個数を求めよ。
海星高校
等しい角はどれ? 近江高校
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
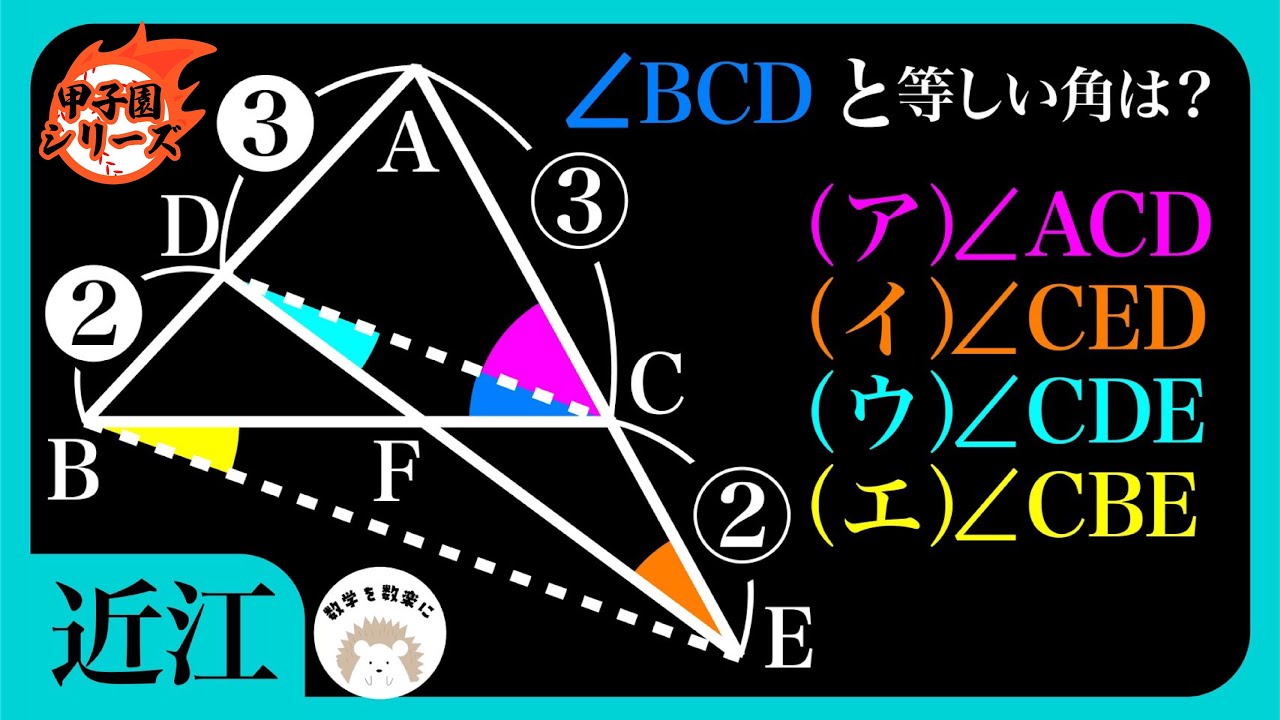
$\angle BCD$と等しい角は?
(ア)$\angle ACD$
(イ)$\angle CED$
(ウ)$\angle CDE$
(エ)$\angle CBE$
*図は動画内参照
近江高等学校
この動画を見る
$\angle BCD$と等しい角は?
(ア)$\angle ACD$
(イ)$\angle CED$
(ウ)$\angle CDE$
(エ)$\angle CBE$
*図は動画内参照
近江高等学校
【「条件付き」の場合は…!】二次方程式:高知県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$x^2+2x-14=0$の解を求めなさい.
※「$(x+\triangle)^2=\bigcirc$」の形に変形して平方根の考え方を使って解くこと.
高知県公立高等学校過去問
この動画を見る
2次方程式$x^2+2x-14=0$の解を求めなさい.
※「$(x+\triangle)^2=\bigcirc$」の形に変形して平方根の考え方を使って解くこと.
高知県公立高等学校過去問
気付けば一瞬です。 星稜
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
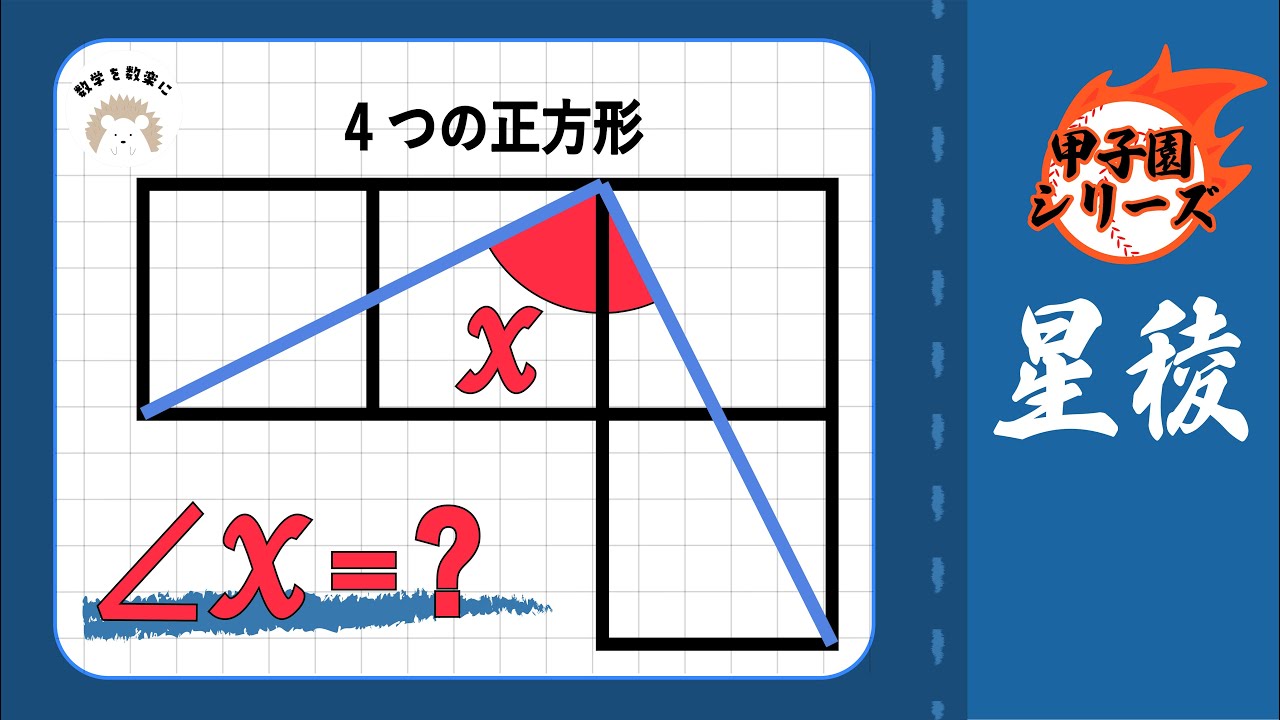
$\angle x = ?$
*図は動画内参照
星稜高等学校
この動画を見る
$\angle x = ?$
*図は動画内参照
星稜高等学校
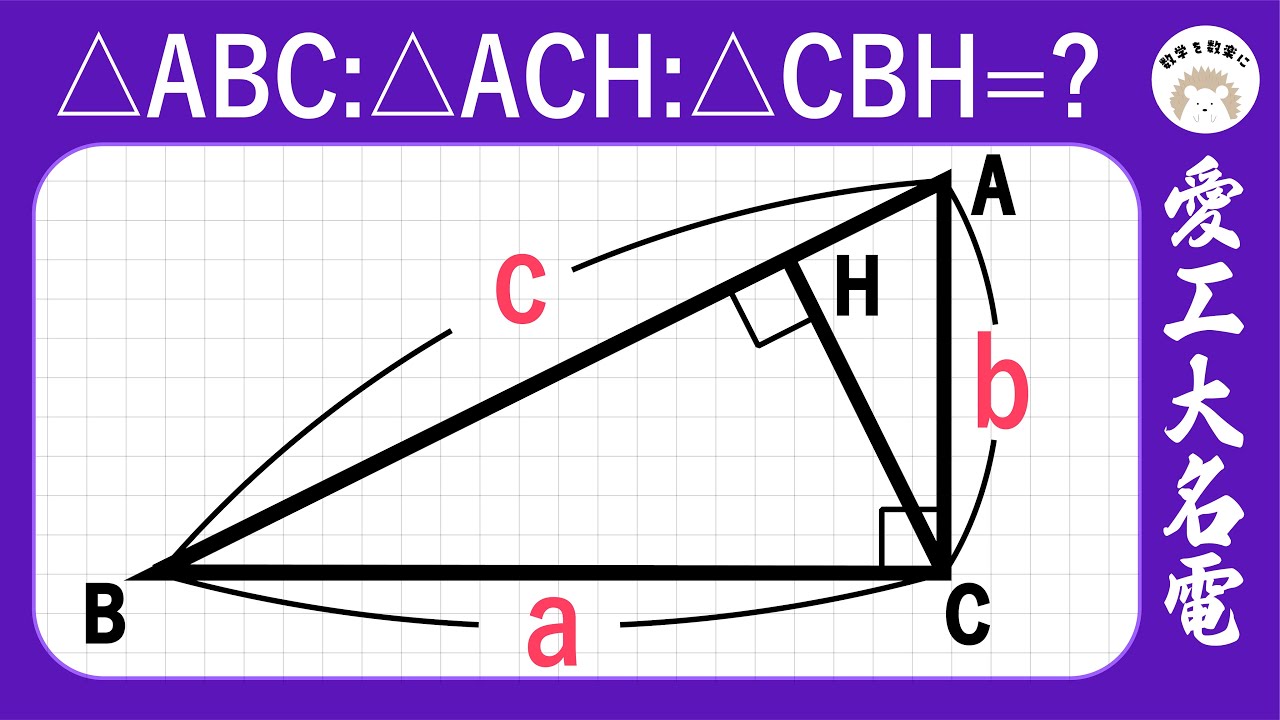
問題の背景まで気付いて一流 愛工大名電
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC:△ACH:△CBH=?
*図は動画内参照
愛知工業大学名電高等学校(改)
この動画を見る
△ABC:△ACH:△CBH=?
*図は動画内参照
愛知工業大学名電高等学校(改)
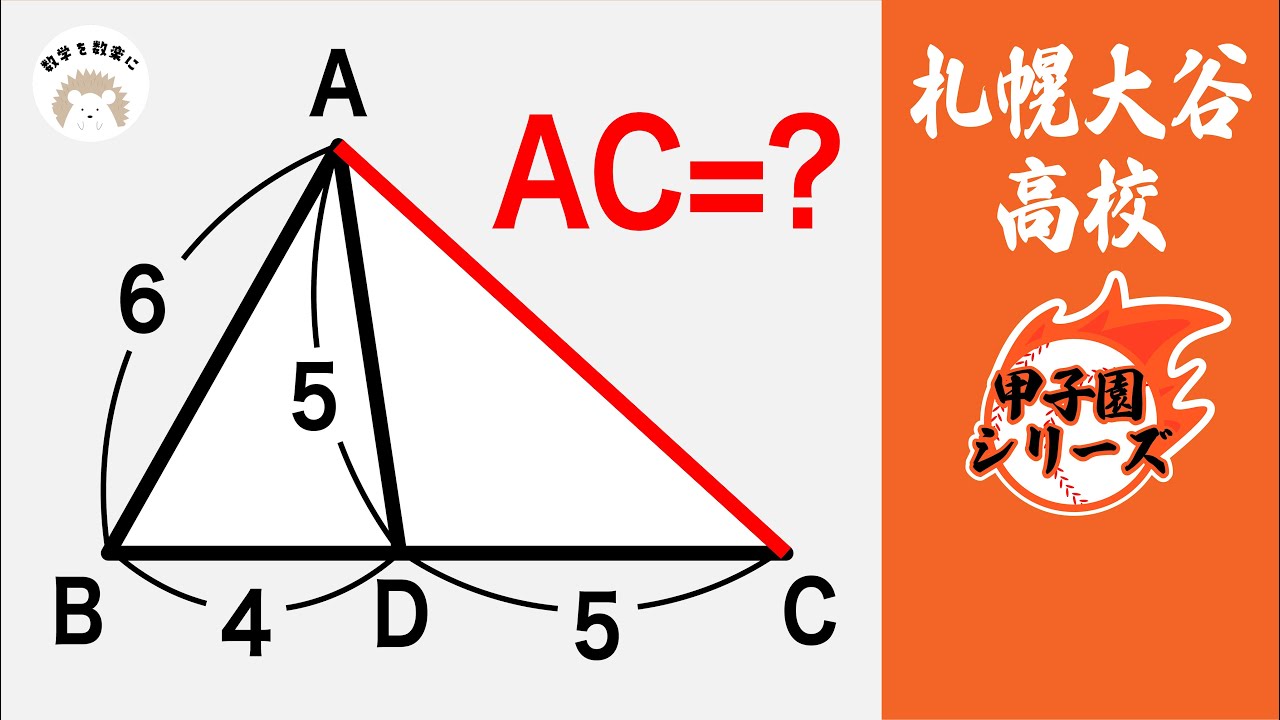
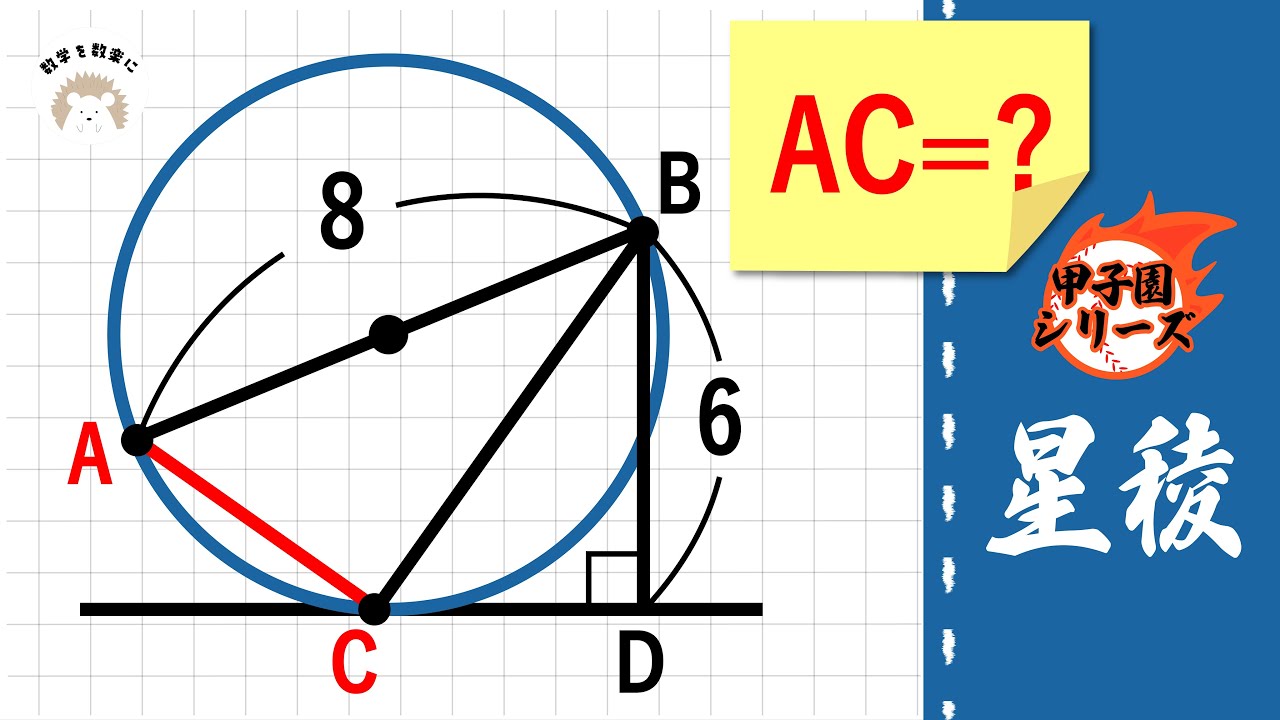
円 星稜
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=?
*図は動画内参照
星稜高等学校
この動画を見る
AC=?
*図は動画内参照
星稜高等学校
【中学数学】連立方程式の宿題Live【中2夏期講習①】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle (1)\,
\begin{cases}
4x-3y=-5\\
y=3x
\end{cases}
$
$\displaystyle (2)\,
\begin{cases}
-2x+3y=17\\
5x+9y=7
\end{cases}
$
$\displaystyle (3)\,
\begin{cases}
4x+y=3\\
7x+5y=-11
\end{cases}
$
$\displaystyle (4)\,
\begin{cases}
2x+3y=13\\
y=2x-1
\end{cases}
$
$\displaystyle (5)\,
\begin{cases}
9x-5y=34\\
6x+8y=17
\end{cases}
$
$\displaystyle (6)\,
\begin{cases}
4x+9y=37\\
7x+5y=11
\end{cases}
$
この動画を見る
$\displaystyle (1)\,
\begin{cases}
4x-3y=-5\\
y=3x
\end{cases}
$
$\displaystyle (2)\,
\begin{cases}
-2x+3y=17\\
5x+9y=7
\end{cases}
$
$\displaystyle (3)\,
\begin{cases}
4x+y=3\\
7x+5y=-11
\end{cases}
$
$\displaystyle (4)\,
\begin{cases}
2x+3y=13\\
y=2x-1
\end{cases}
$
$\displaystyle (5)\,
\begin{cases}
9x-5y=34\\
6x+8y=17
\end{cases}
$
$\displaystyle (6)\,
\begin{cases}
4x+9y=37\\
7x+5y=11
\end{cases}
$
斜線部の面積を求めよ 樹徳高校

【手順は限られるのか】因数分解:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川学園取手高等学校
この動画を見る
$a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川学園取手高等学校
2個のサイコロの確率 普通に数えあげてもいいけど。。。樹徳高校

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2つのサイコロA,Bを投げる。
Aの出る目>Bの出る目となる確率は?
樹徳高等学校
この動画を見る
2つのサイコロA,Bを投げる。
Aの出る目>Bの出る目となる確率は?
樹徳高等学校
受験テクニック満載 受験生よ見よ 日大三島
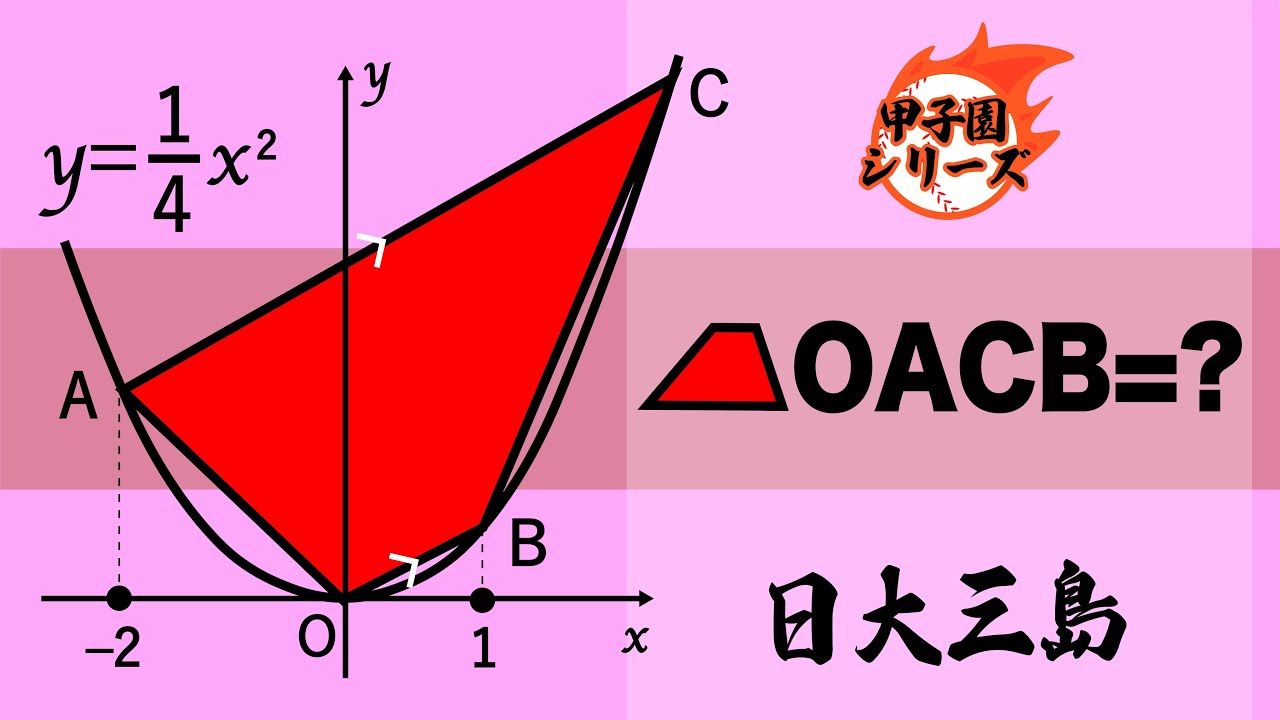
斜線部の面積=❓ 日大三島
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
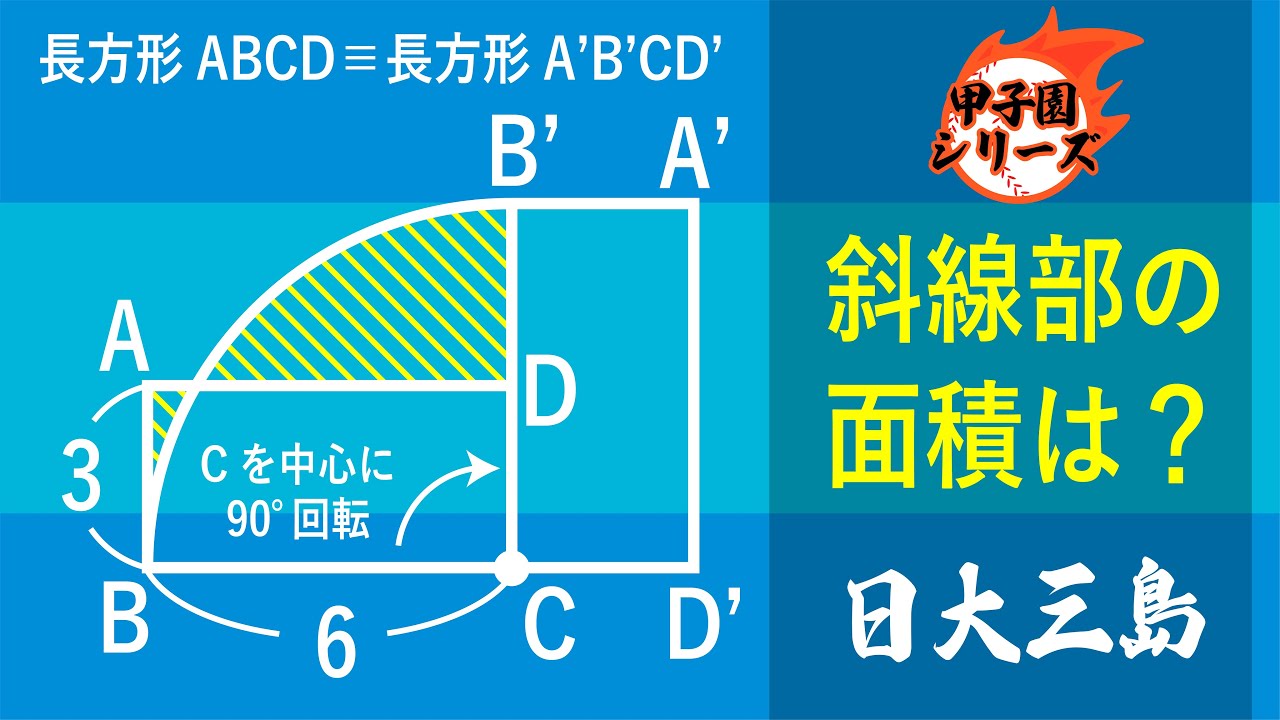
長方形ABCD≡長方形A'B'C'D'
斜線部の面積は?
*図は動画内参照
日本大学三島高等学校
この動画を見る
長方形ABCD≡長方形A'B'C'D'
斜線部の面積は?
*図は動画内参照
日本大学三島高等学校
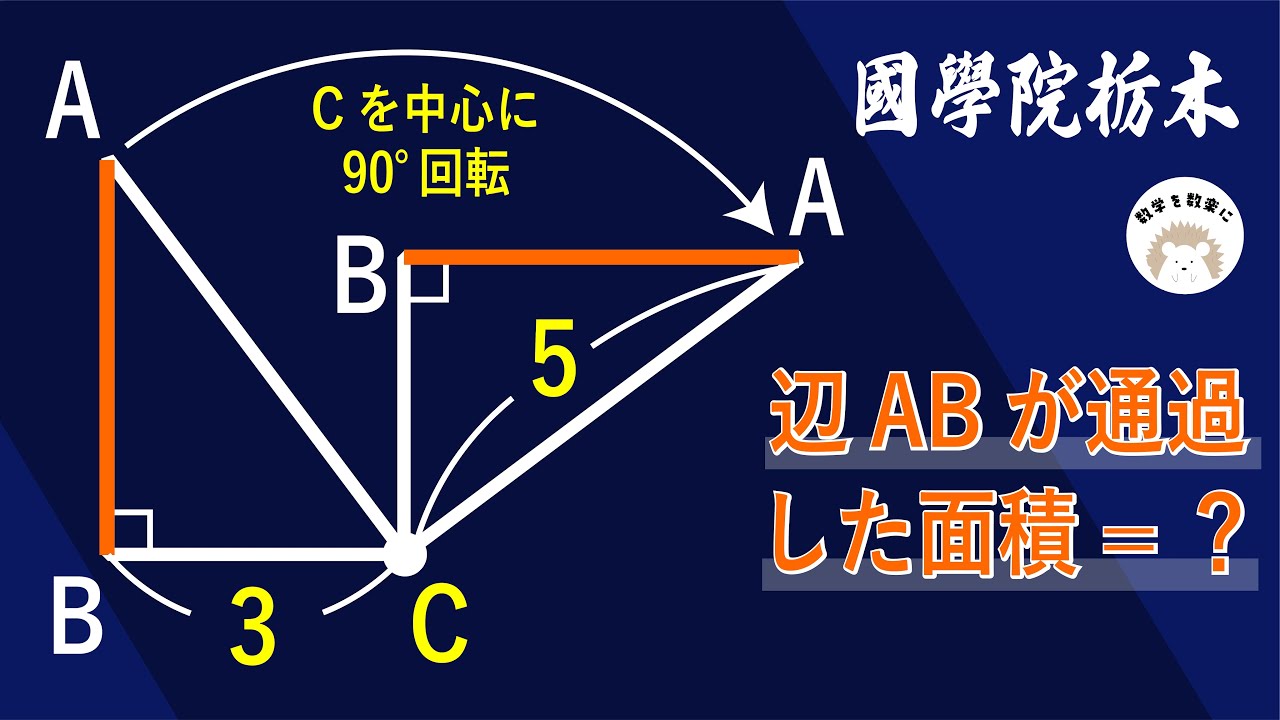
直角三角形の回転移動 國學院栃木
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
Cを中心に90°回転
辺ABが通過した面積=?
*図は動画内参照
國學院大學栃木高等学校
この動画を見る
Cを中心に90°回転
辺ABが通過した面積=?
*図は動画内参照
國學院大學栃木高等学校
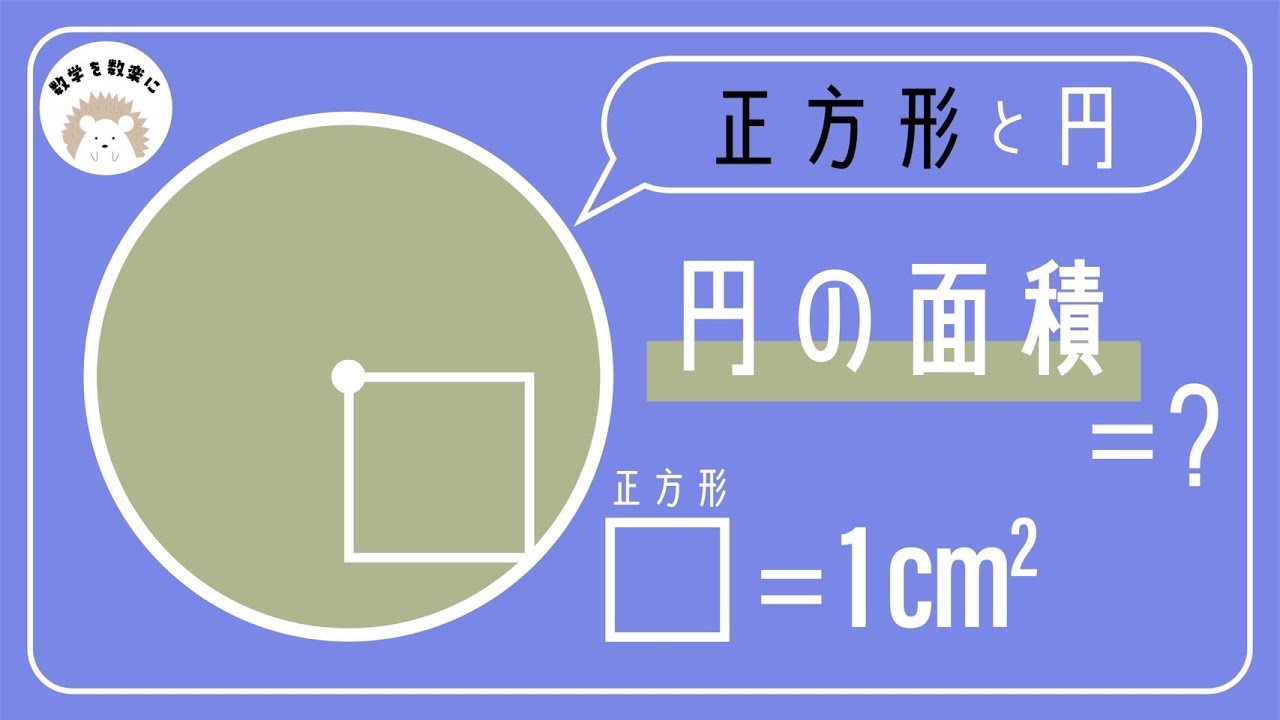
小学生も解ける!? 円の面積