 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
円周角 日大山形

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x=?$
*点は円周を10等分する点
*図は動画内参照
日本大学山形高等学校
この動画を見る
$\angle x=?$
*点は円周を10等分する点
*図は動画内参照
日本大学山形高等学校
円周角 三重高校

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x=?$
*図は動画内参照
三重高等学校
この動画を見る
$\angle x=?$
*図は動画内参照
三重高等学校
智弁和歌山 誰もが一度 ハマったことのある意外な落とし穴とは? 式の値

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a-b=3,ab=3$のとき
$2a^2+2b^2=$
智弁学園和歌山高等学校
この動画を見る
$a-b=3,ab=3$のとき
$2a^2+2b^2=$
智弁学園和歌山高等学校
筆算したいならすればいいさ 二松学舎大学附属

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
18×19×20×21×22 =
二松学舎大学附属高等学校
この動画を見る
18×19×20×21×22 =
二松学舎大学附属高等学校
【中学数学】2次方程式の基礎を学ぼう~数学苦手な人は見てね~ 3-1【中3数学】

大阪桐蔭 角の和

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
赤の角の和は何度?
*図は動画内参照
大阪桐蔭高等学校
この動画を見る
赤の角の和は何度?
*図は動画内参照
大阪桐蔭高等学校
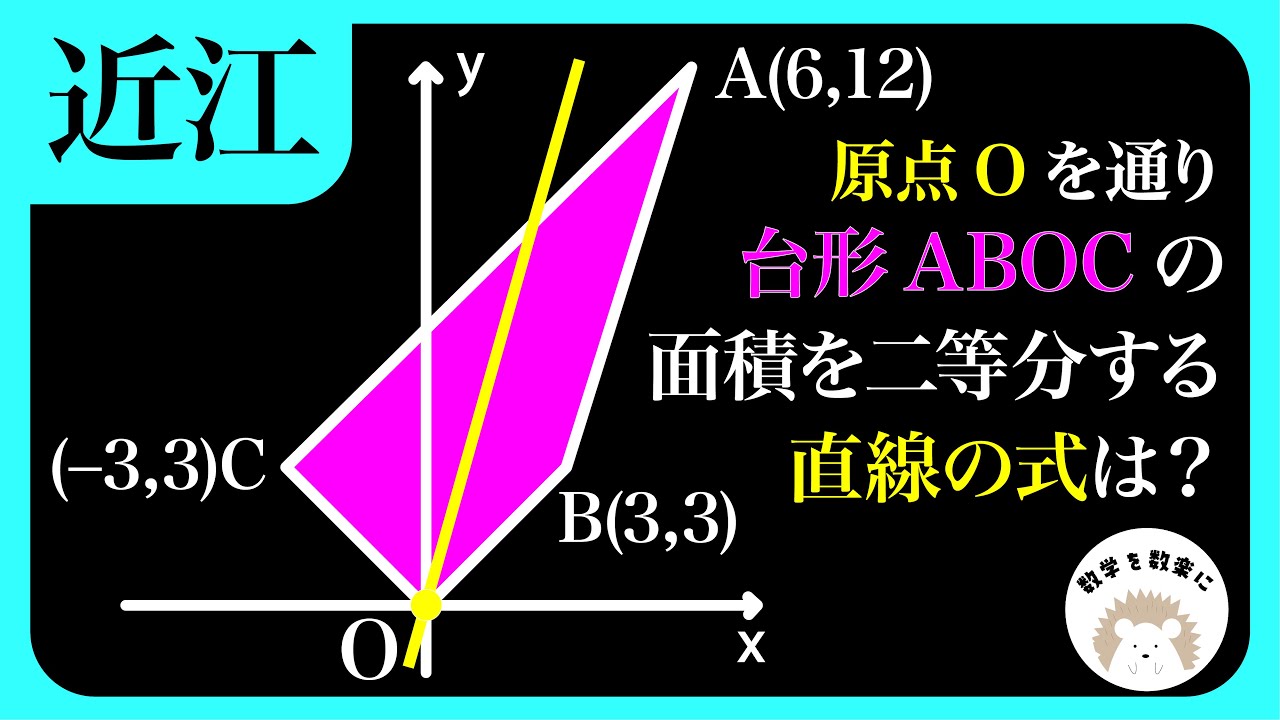
近江高校 台形の面積二等分
単元:
#数学(中学生)#中2数学#数Ⅱ#図形と方程式#点と直線#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABOCの面積を2等分する直線の式は?
*図は動画内参照
近江高等学校
この動画を見る
四角形ABOCの面積を2等分する直線の式は?
*図は動画内参照
近江高等学校
約数の個数が3個 専修大学松戸

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1~50の自然数の中で約数が3コである数は全部で何コ?
専修大学松戸高等学校
この動画を見る
1~50の自然数の中で約数が3コである数は全部で何コ?
専修大学松戸高等学校
20%引きしてから20%増ししても元には戻りませんよ 神戸国際大学附属

単元:
#数学(中学生)#文章題#単位・比と割合・比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
ある地図を80%の倍率で縮小した。
元の地図と同じにするには何%の倍率で拡大すればよいか。
*図は動画内参照
神戸国際大学附属高等学校
この動画を見る
ある地図を80%の倍率で縮小した。
元の地図と同じにするには何%の倍率で拡大すればよいか。
*図は動画内参照
神戸国際大学附属高等学校
【3分でOK!定石を身に付ける!】計算:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
【西暦を含む数学問題】 計算しなさい。
$2021 \times 2019 - 2018^2 - 2020 \times 2023 + 2019^2 +2020$
この動画を見る
入試問題 立命館高等学校
【西暦を含む数学問題】 計算しなさい。
$2021 \times 2019 - 2018^2 - 2020 \times 2023 + 2019^2 +2020$
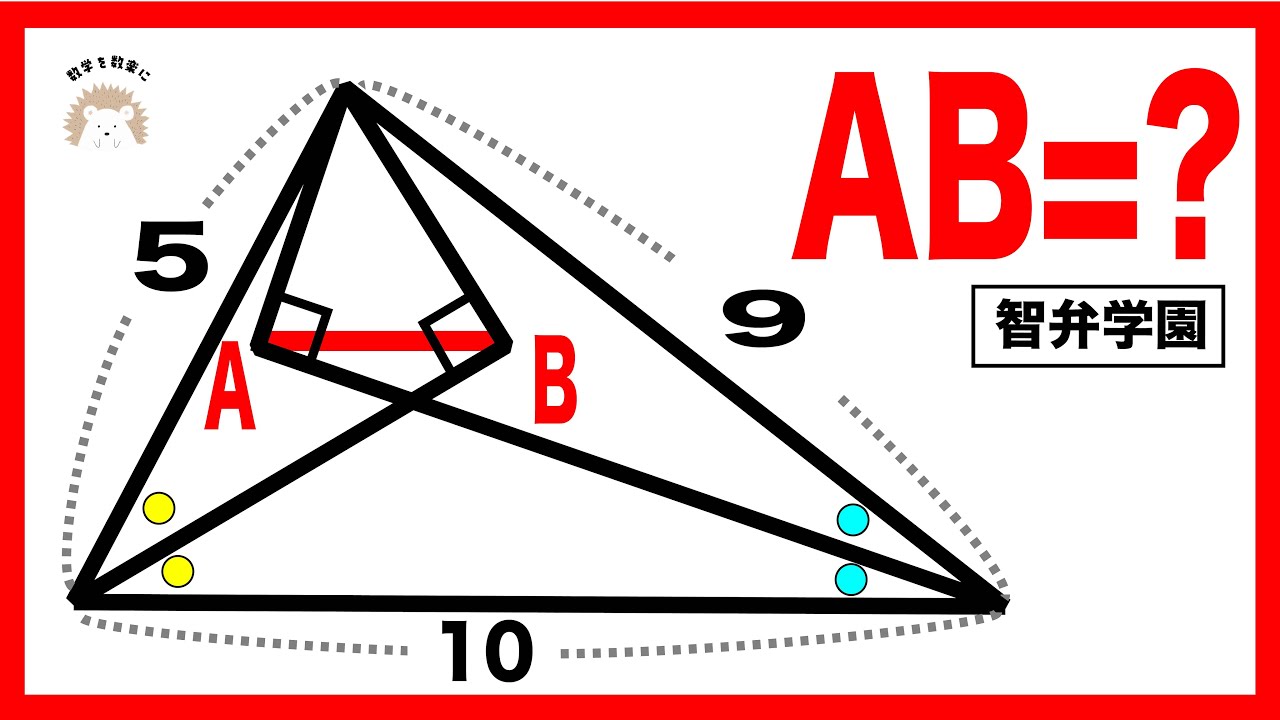
智弁学園(改)角の二等分線➕垂線
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=?
*図は動画内参照
智弁学園高等学校(改)
この動画を見る
AB=?
*図は動画内参照
智弁学園高等学校(改)
関数の問題にみえて実は。。新田高校
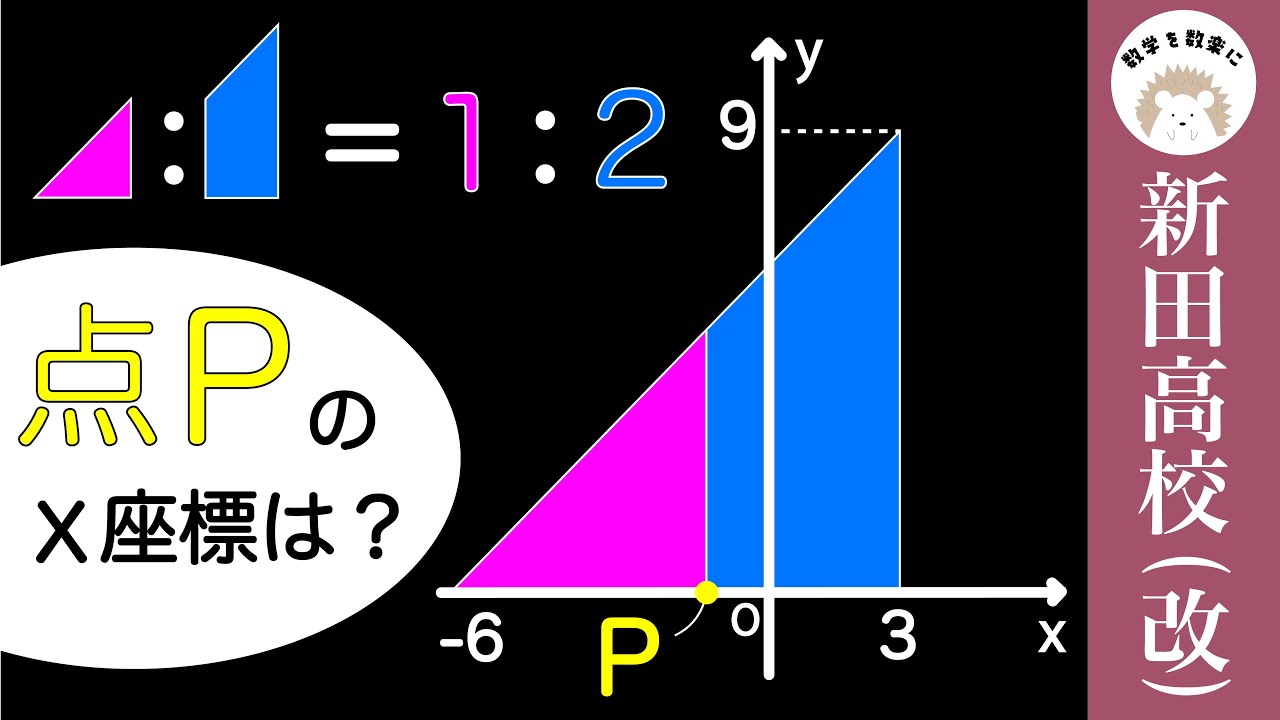
単元:
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pの座標は?
*図は動画内参照
新田高等学校
この動画を見る
点Pの座標は?
*図は動画内参照
新田高等学校
日大山形 (改)円と角 2通りで解説
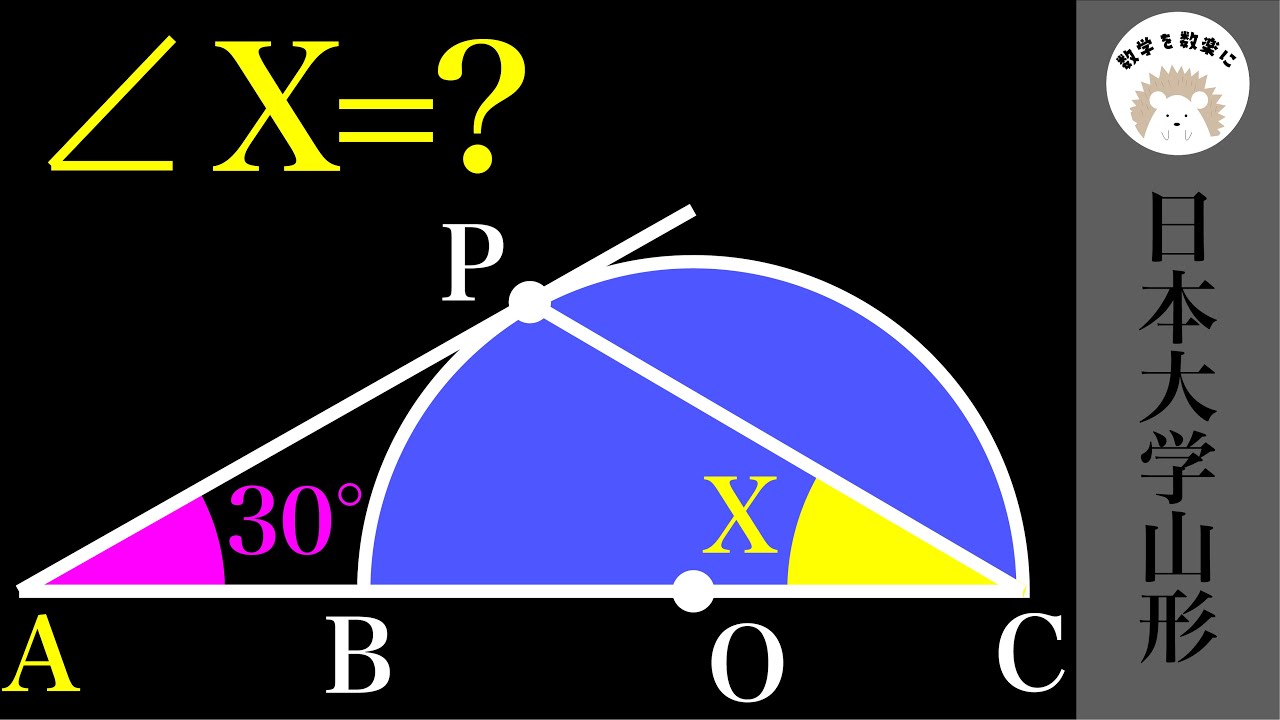
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x=?$
*図は動画内参照
日本大学山形高等学校(改)
この動画を見る
$\angle x=?$
*図は動画内参照
日本大学山形高等学校(改)
浦和学院のラスボス
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
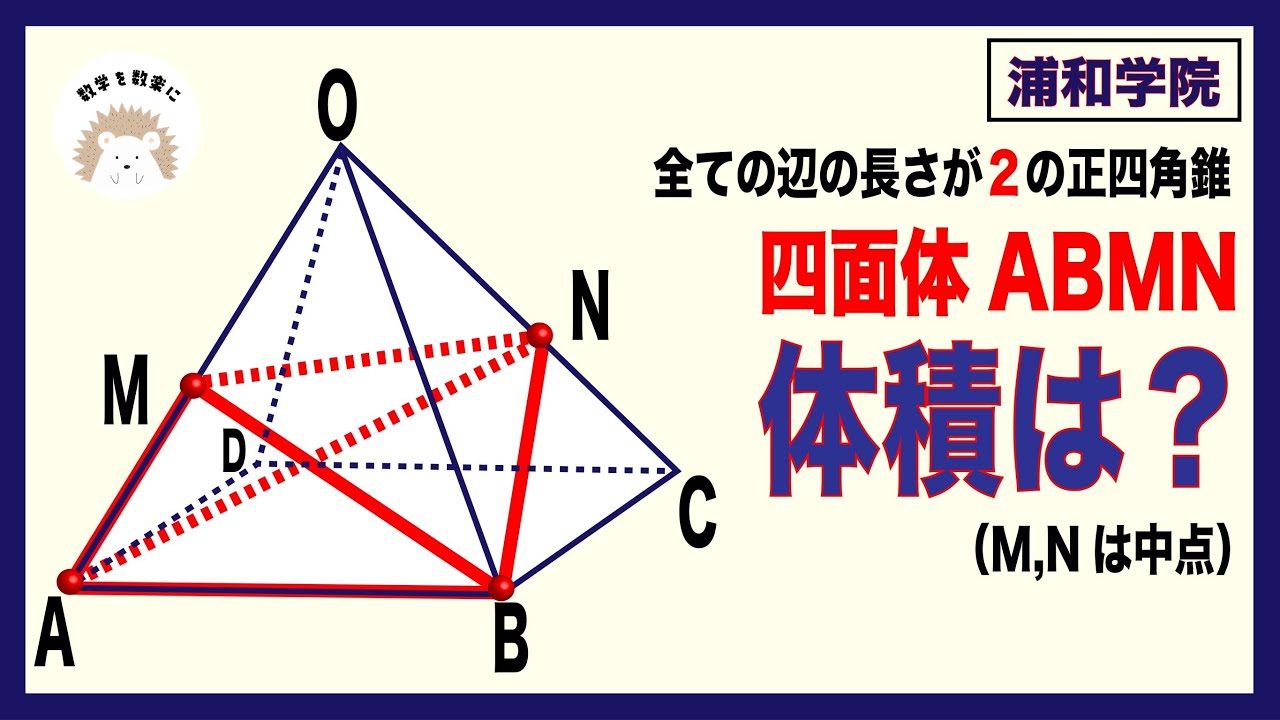
すべての辺の長さが2の正四角錐
四面体ABMNの体積=?
浦和学院高等学校
この動画を見る
すべての辺の長さが2の正四角錐
四面体ABMNの体積=?
浦和学院高等学校
角度 2通りで解説 弘前学院聖愛
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
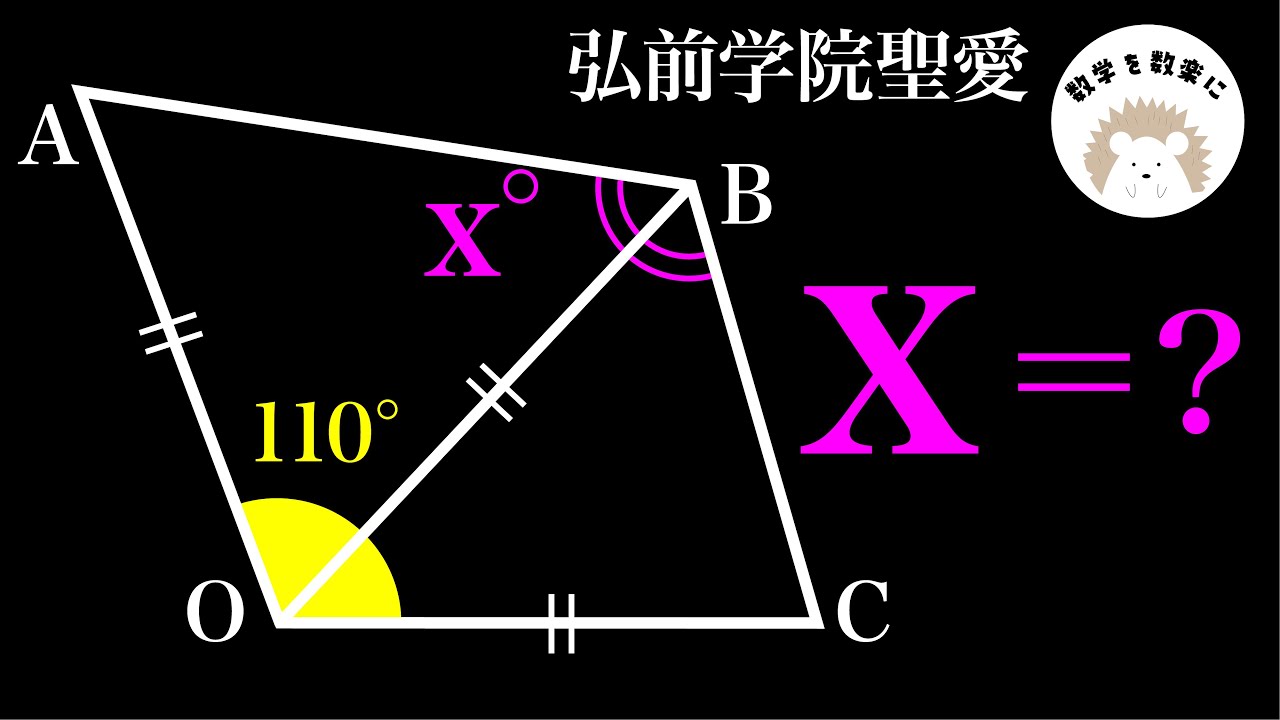
$\angle x=?$
*図は動画内参照
弘前学院聖愛高等学校
この動画を見る
$\angle x=?$
*図は動画内参照
弘前学院聖愛高等学校
石見智翠館(改) 気づけば一瞬!!
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
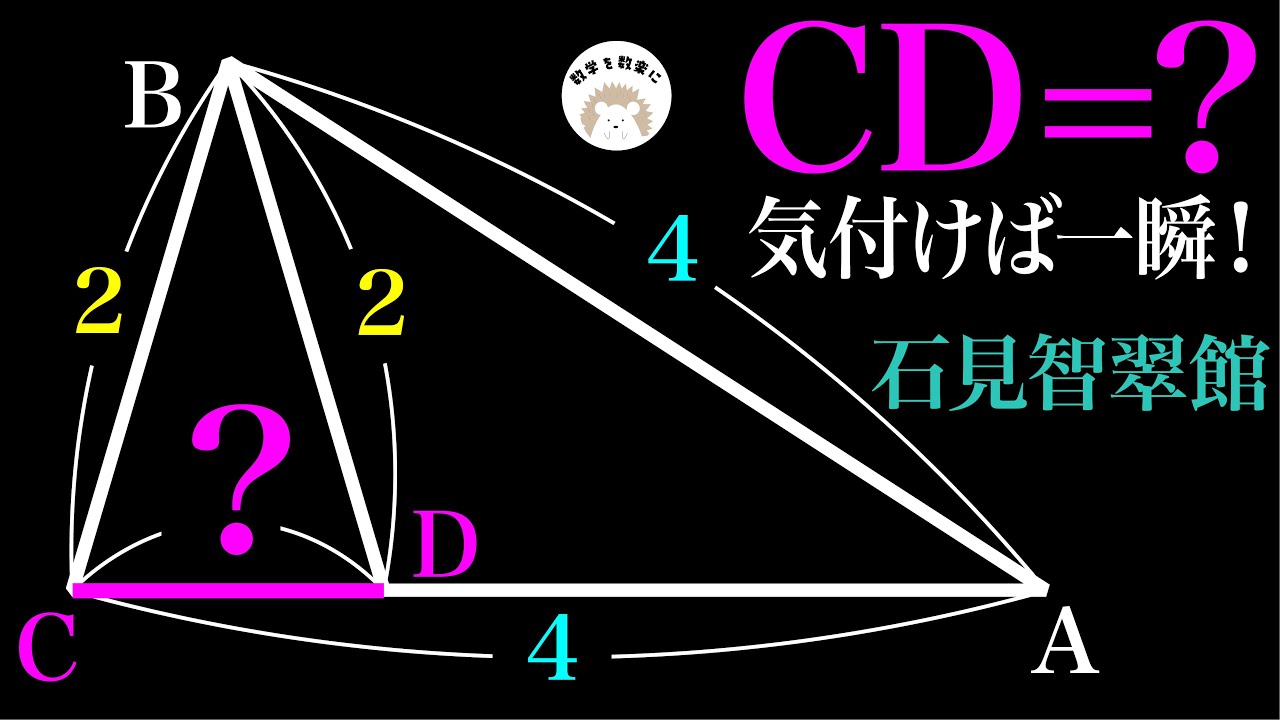
CD=?
*図は動画内参照
石見智翠館高等学校
この動画を見る
CD=?
*図は動画内参照
石見智翠館高等学校
【理解は3分!計算は30秒!】平方根:土浦日本大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#土浦日本大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 土浦日本大学高等学校
次の▬をうめなさい。
$(\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }}{2})^2(\displaystyle \frac{\sqrt{ 5 }-\sqrt{ 3 }}{2})^2=\displaystyle \frac{▬}{▬}$
この動画を見る
入試問題 土浦日本大学高等学校
次の▬をうめなさい。
$(\displaystyle \frac{\sqrt{ 5 }+\sqrt{ 3 }}{2})^2(\displaystyle \frac{\sqrt{ 5 }-\sqrt{ 3 }}{2})^2=\displaystyle \frac{▬}{▬}$
【中学数学】三角形の面積を求める問題演習~解き方と考え方~【中2数学】
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
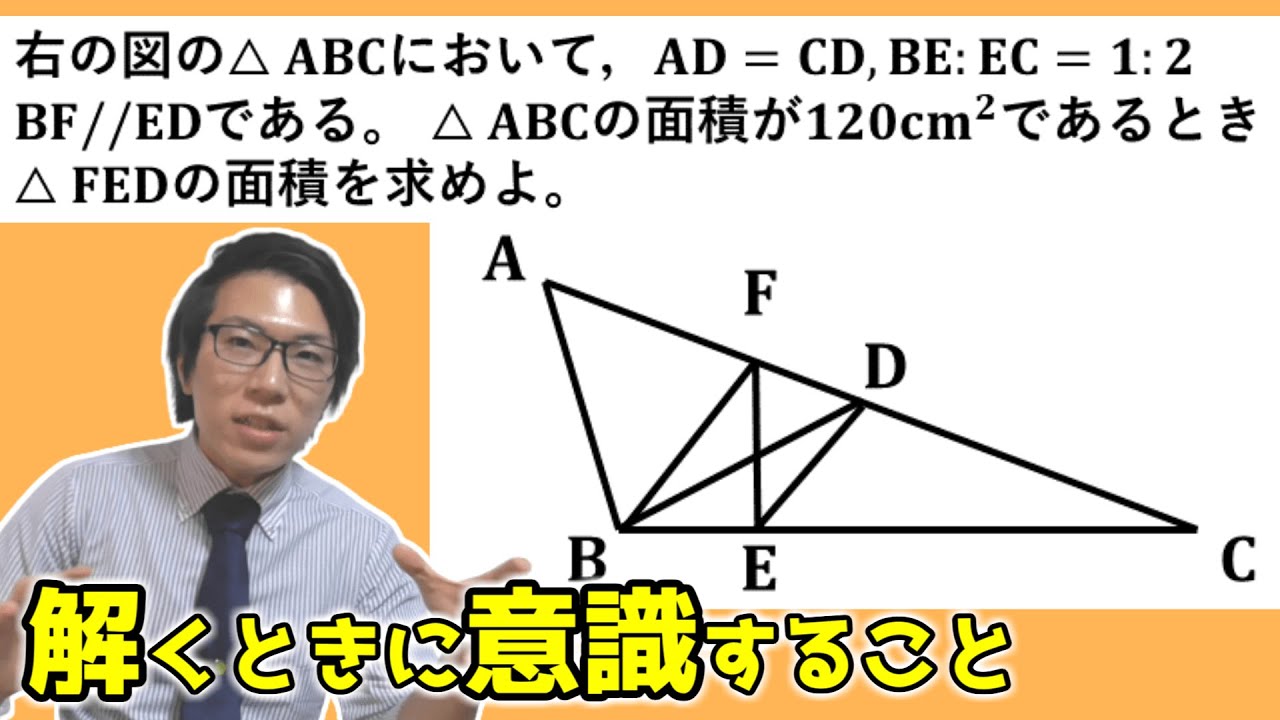
動画内の図の$\triangle ABC$において,$AD=CD$、$BE:EC=1:2 BF//ED$である。
$\triangle ABC$の面積が$120cm^2$であるとき$\triangle FED$の面積を求めよ。
この動画を見る
動画内の図の$\triangle ABC$において,$AD=CD$、$BE:EC=1:2 BF//ED$である。
$\triangle ABC$の面積が$120cm^2$であるとき$\triangle FED$の面積を求めよ。
樟南高校 知っていれば一瞬!!
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
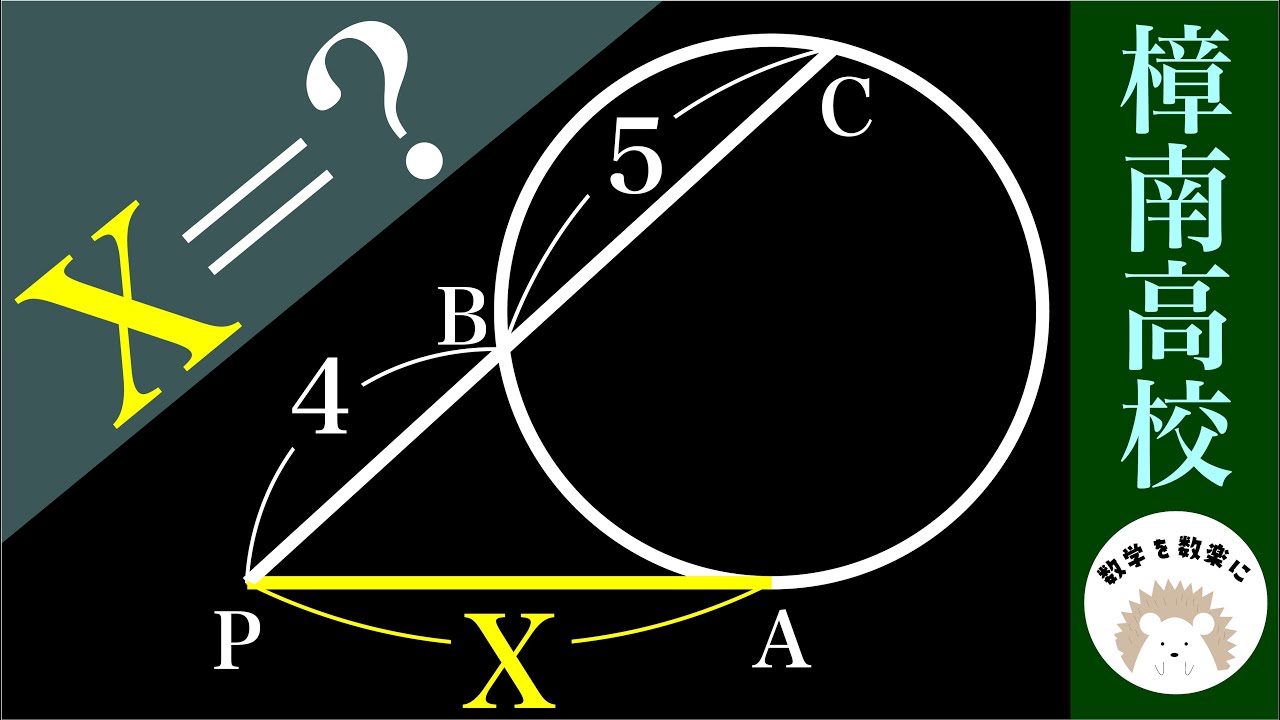
問題文全文(内容文):
x=?
*図は動画内参照
樟南高等学校
この動画を見る
x=?
*図は動画内参照
樟南高等学校
三重高校 面倒な計算はいらない。
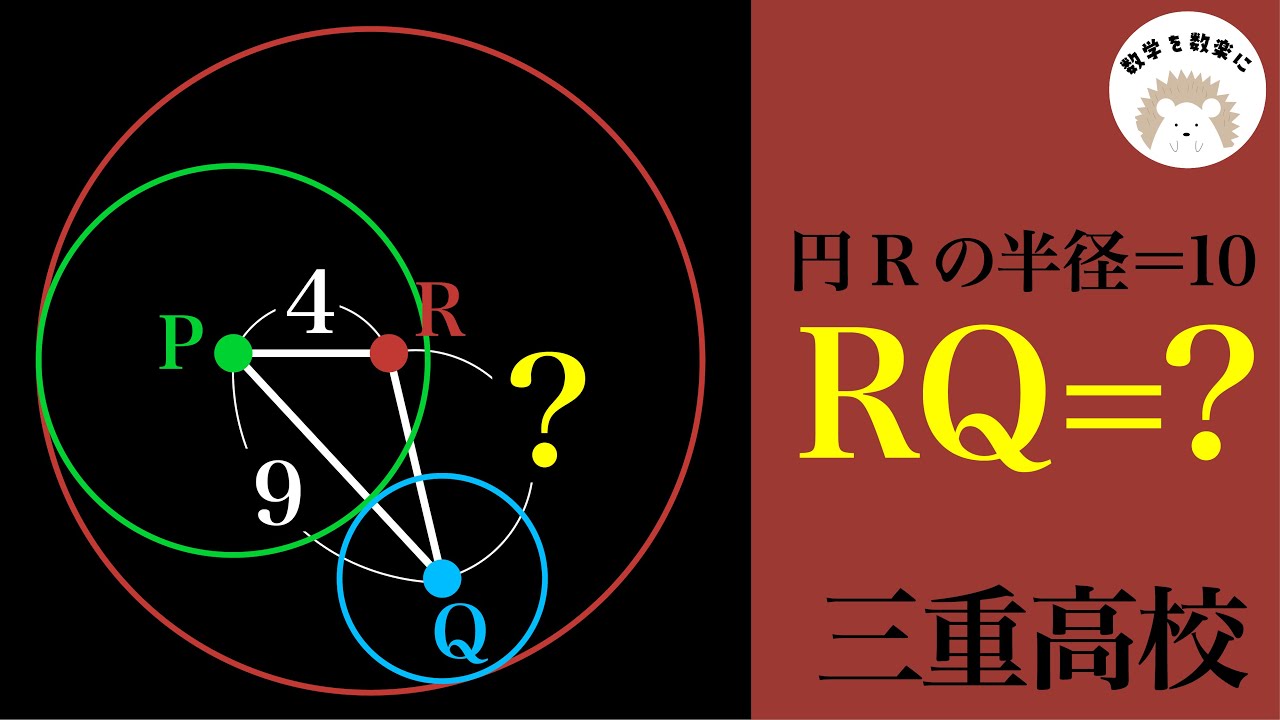
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
P,Q,Rはそれぞれの円の中心
円Rの半径=10
RQ=?
*図は動画内参照
三重高等学校
この動画を見る
P,Q,Rはそれぞれの円の中心
円Rの半径=10
RQ=?
*図は動画内参照
三重高等学校
二松学舎大学附属 因数分解 2通りで解説

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2b^2-a^2-b^2+1$を因数分解せよ
二松学舎大学附属高等学校
この動画を見る
$a^2b^2-a^2-b^2+1$を因数分解せよ
二松学舎大学附属高等学校
中央値(メジアン)とは? 日大東北

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
6人のハンドボール投げの記録
x,19,12,23,9,13
中央値=15(m)のとき
x=?
日本大学東北高等学校
この動画を見る
6人のハンドボール投げの記録
x,19,12,23,9,13
中央値=15(m)のとき
x=?
日本大学東北高等学校
円とおうぎ形と放物線 おうぎ形の面積=? 近江高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
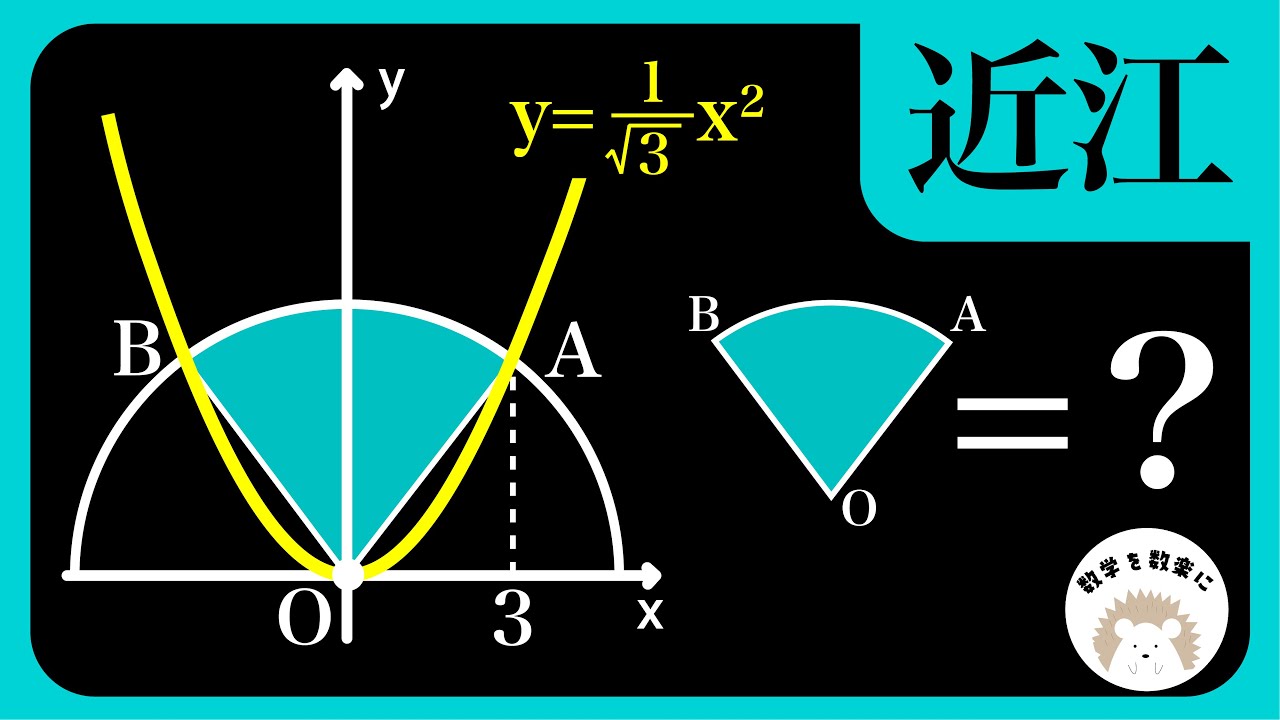
問題文全文(内容文):
おうぎ形OAB=?
*図は動画内参照
近江高等学校
この動画を見る
おうぎ形OAB=?
*図は動画内参照
近江高等学校
作新学院 立方体の切断
単元:
#数学(中学生)#立体図形#立体切断#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
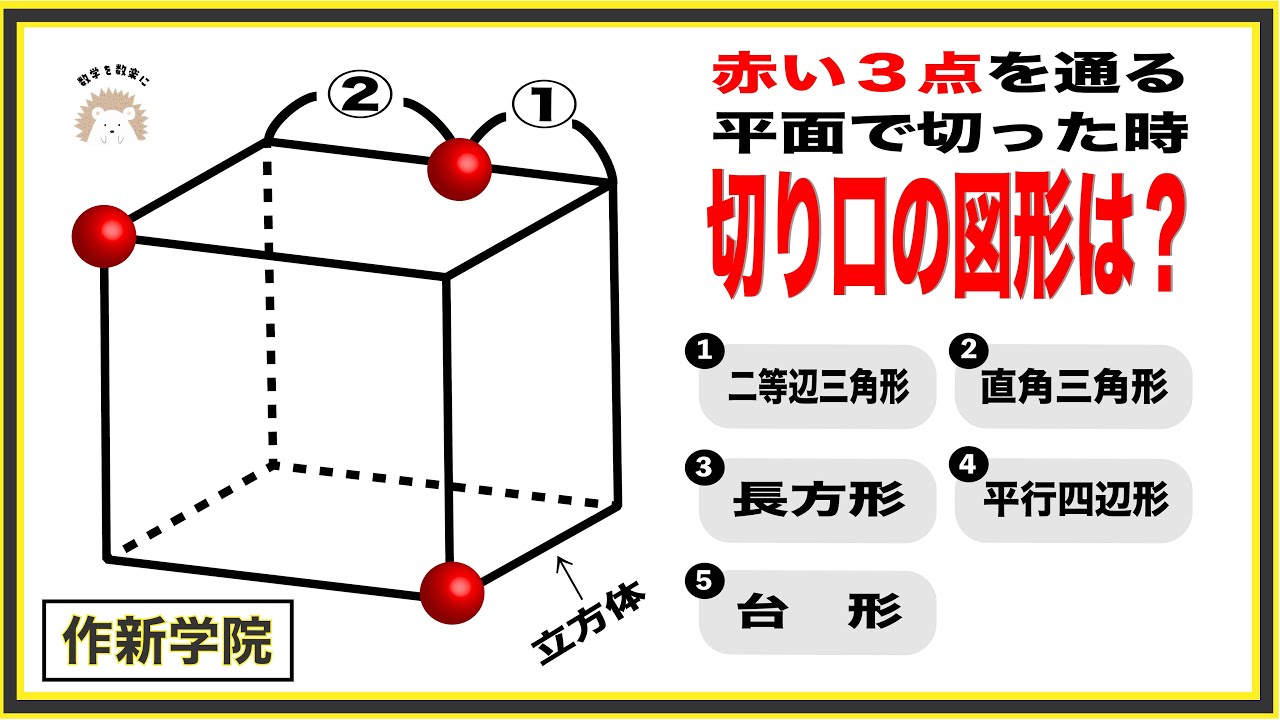
問題文全文(内容文):
立方体
赤い3点を通る平面で切ったとき切り口の図形は?
①二等辺三角形 ②直角三角形 ③長方形 ④平行四辺形 ⑤台形
*図は動画内参照
作新学院高等学校
この動画を見る
立方体
赤い3点を通る平面で切ったとき切り口の図形は?
①二等辺三角形 ②直角三角形 ③長方形 ④平行四辺形 ⑤台形
*図は動画内参照
作新学院高等学校
9の引き算の新たな計算方法発見した

入試では珍しいあの条件 前橋育英
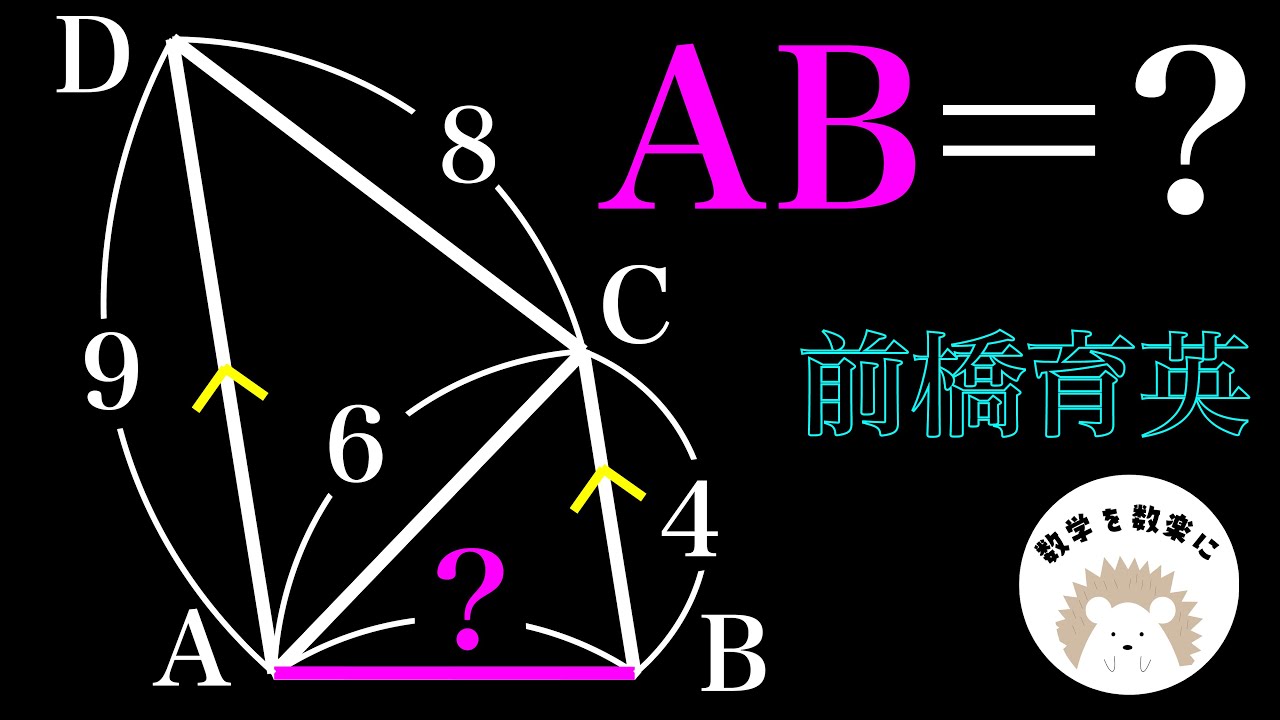
【3分でつかむ!中学数学の計算!】文字式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
$a=2,b=-\displaystyle \frac{1}{3}$
のとき
$(-\displaystyle \frac{3b^2}{a}) \div (-\displaystyle \frac{1}{2}ab^2)^3 \times \displaystyle \frac{2}{9}a^3b$
の値を求めよ。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
$a=2,b=-\displaystyle \frac{1}{3}$
のとき
$(-\displaystyle \frac{3b^2}{a}) \div (-\displaystyle \frac{1}{2}ab^2)^3 \times \displaystyle \frac{2}{9}a^3b$
の値を求めよ。
日大東北 筆算してもいいけど解けるかな?
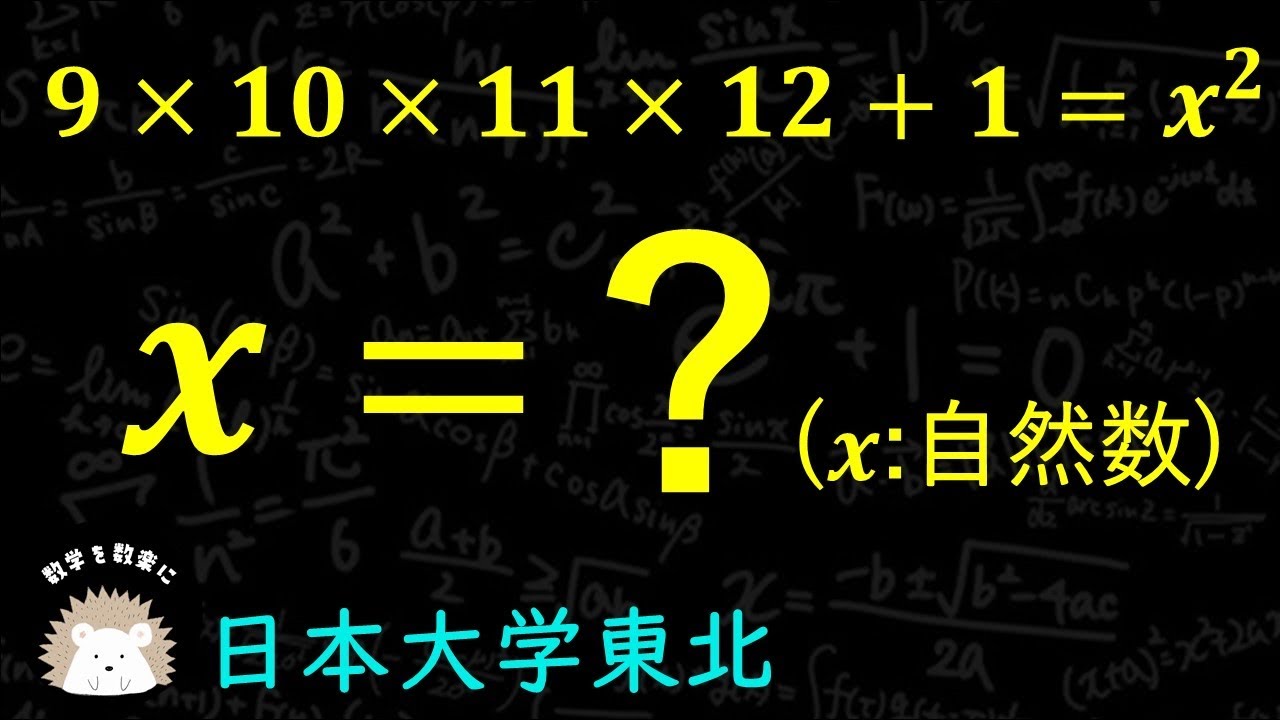
単元:
#計算と数の性質#いろいろな計算#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$9×10×11×12+1 = x^2$(xは自然数)
日本大学東北高等学校
この動画を見る
$9×10×11×12+1 = x^2$(xは自然数)
日本大学東北高等学校
近江高校 立方体の展開図
単元:
#数学(中学生)#立体図形#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
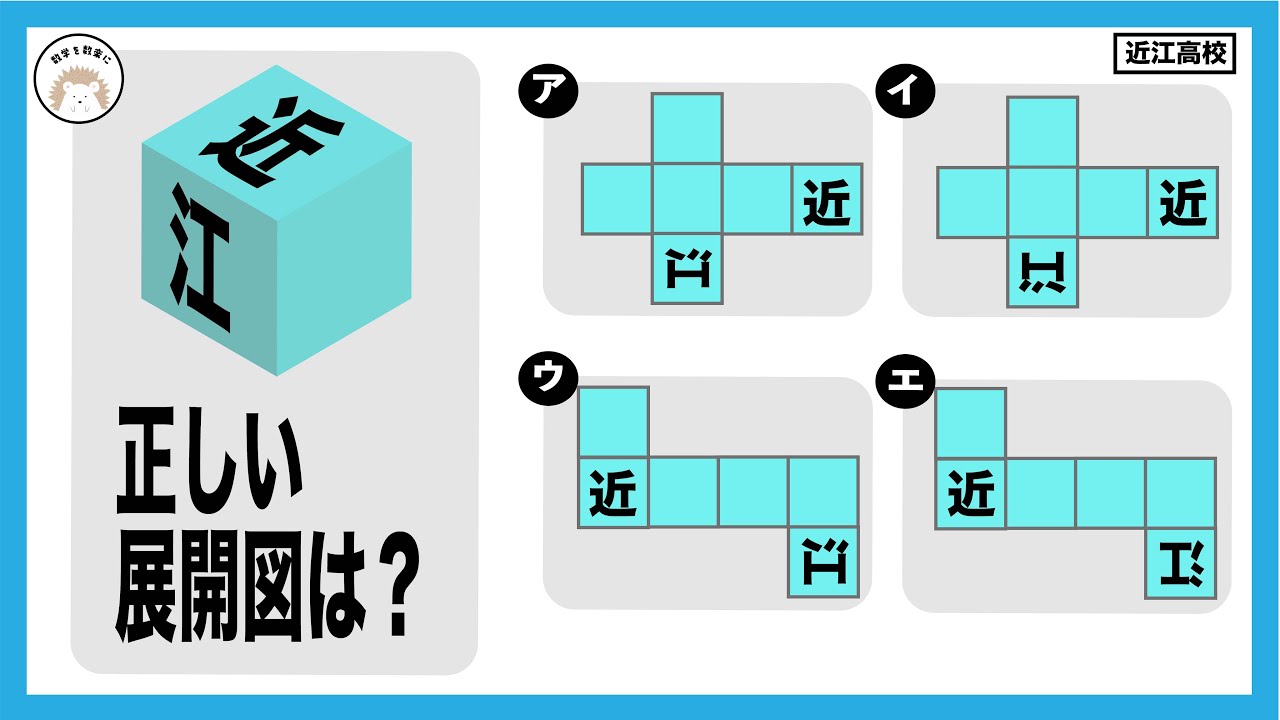
正しい展開図は?
(ア)(イ)(ウ)(エ)
*図は動画内参照
近江高等学校
この動画を見る
正しい展開図は?
(ア)(イ)(ウ)(エ)
*図は動画内参照
近江高等学校
三平方の定理使わずに解ける?中学入試 甲陽学院
単元:
#算数(中学受験)#数学(中学生)#中3数学#三平方の定理#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
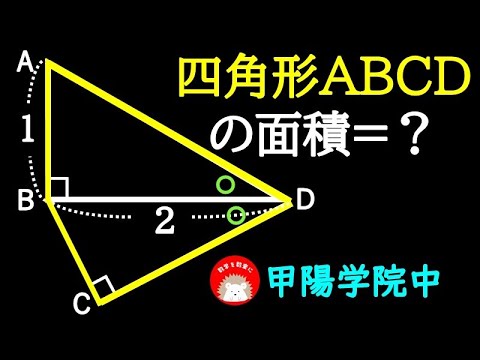
四角形ABCDの面積=?
*図は動画内参照
甲陽学院中学校
この動画を見る
四角形ABCDの面積=?
*図は動画内参照
甲陽学院中学校
