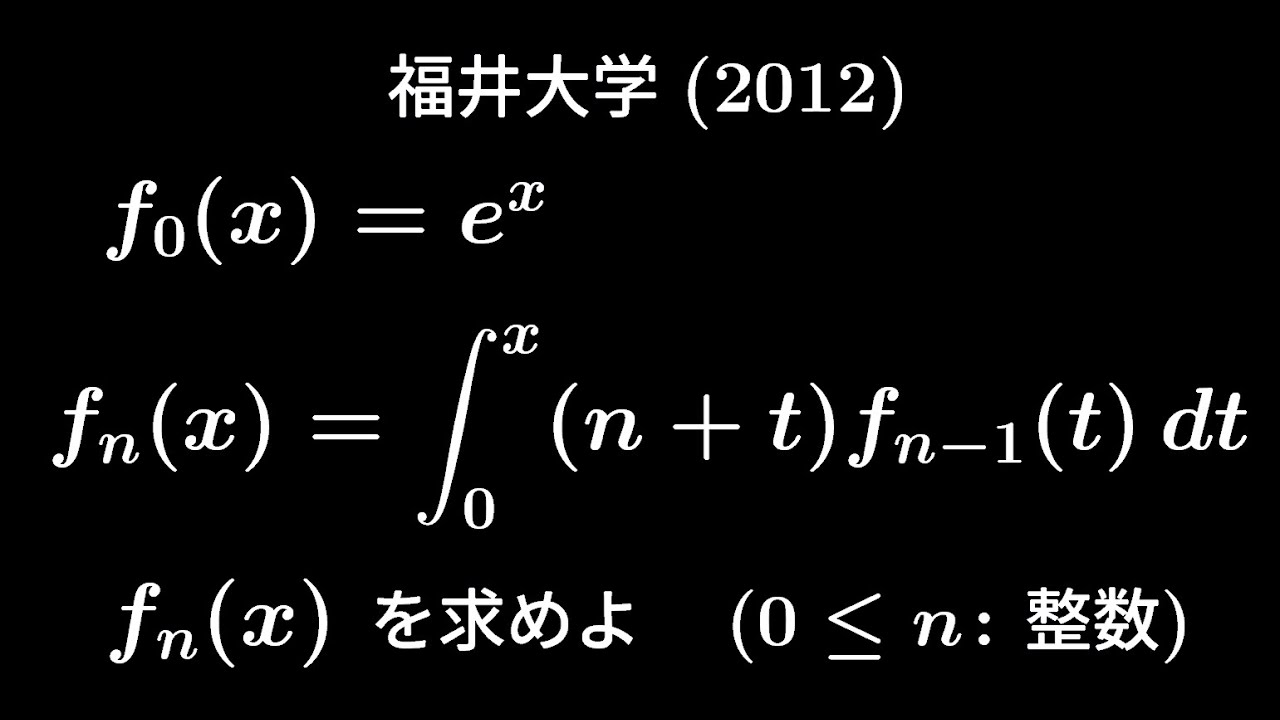🟨＝❓ 解けたら天才⁉️ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数B > 数列 > 数列とその和（等差・等比・階差・Σ） > 🟨＝❓　解けたら天才⁉️

🟨＝❓　解けたら天才⁉️

問題文全文(内容文)：
1▢=1
2▢=2
3▢=6
▢=?
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： 数学を数楽に
問題文全文(内容文)：
1▢=1
2▢=2
3▢=6
▢=?
投稿日：2021.06.03

＜関連動画＞

確率　漸化式

アイキャッチ画像
単元： #数列#漸化式#数学(高校生)#数B
指導講師： 鈴木貫太郎
問題文全文(内容文)：
サイコロを$n$回振って,出た目の積を5で割った余りが1である確率$p_n$を求めよ.
この動画を見る　

数検準１級　三項間漸化式　極限　高校数学

アイキャッチ画像
単元： #数学検定・数学甲子園・数学オリンピック等#数列#漸化式#数学検定#数学検定準1級#数学(高校生)#数B
指導講師： 鈴木貫太郎
問題文全文(内容文)：
（1）
$A \neq 0$　$a_{1}=1, a_{2}=2A$
$a_{n+2}=2Aa_{n+1}-A^2a_{n}$
一般項を求めよ。


（2）
$\displaystyle \lim_{ x \to \infty }x^2(1=\cos^3 \displaystyle \frac{1}{x})$
極限値を求めよ。

出典：数学検定準１級　過去問
この動画を見る　

【高校数学】　数B－５８　等差数列とその和②

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
①初項3,公差4の等差数列において,47となる項は第何項か求めよう.

②$4,k,6k$が等差数列であるとき,$k$の値を求めよう.

③第10項が31,第25項が76である等差数列$\{a_n \}$の一般項を求めよう.
この動画を見る　

【数B】【数列】初項4、公差５の等差数列{a_n}と、初項８，公差7の等差数列{b_n}について、これら2つの数列に共通に含まれている項を、順に並べてできる数列{c_n}の一般項を求めよ。

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
教材： #4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#中高教材#数列
指導講師： 理数個別チャンネル
問題文全文(内容文)：
初項4、公差５の等差数列${a_n}$と、初項８，公差7の等差数列${b_n}$について、これら2つの数列に共通に含まれている項を、順に並べてできる数列${c_n}$の一般項を求めよ。
この動画を見る　

福田のおもしろ数学284〜(1+1/n)^nが増加数列である証明

アイキャッチ画像
単元： #数列#漸化式#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
数列 $ \large{ a }\scriptsize{ n } = \left(1+\frac{1}{n} \right)^n $ は増加することを証明せよ。
この動画を見る　
PAGE TOP