 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
どう覚えた?

【中学理科】有色鉱物と無色鉱物の語呂合わせ~火成岩から復習~【中1理科】

【高校数学】和の記号・シグマの公式の証明 3-8.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次式を証明せよ。
$\displaystyle \sum_{i=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
$\displaystyle \sum_{i=1}^n k^3=\{ \frac{1}{2}n(n+1)\}^2$
この動画を見る
次式を証明せよ。
$\displaystyle \sum_{i=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
$\displaystyle \sum_{i=1}^n k^3=\{ \frac{1}{2}n(n+1)\}^2$
フェルマーの最終定理の証明

【中学数学】さいころの確率~まじで点数取りどころ~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問 大小2つのさいころを同時に投げるとき、次の確率を求めよ。
(1) 出る目の和が4になる確率
(2) 出る目の和が7になる確率
(3) 出る目の和が9以上になる確率
(4) 出る目の積が4になる確率
(5) 出る目の積が12の倍数になる確率
(6) 出る目の積が10以上になる確率
この動画を見る
問 大小2つのさいころを同時に投げるとき、次の確率を求めよ。
(1) 出る目の和が4になる確率
(2) 出る目の和が7になる確率
(3) 出る目の和が9以上になる確率
(4) 出る目の積が4になる確率
(5) 出る目の積が12の倍数になる確率
(6) 出る目の積が10以上になる確率
【裏技】確率のこれ知ってる?

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
袋の中に赤玉2個、白玉1個青玉1個が入っている。
この中から同時に2個とり出すとき。2個とも赤玉である確率を求めよ。
この動画を見る
袋の中に赤玉2個、白玉1個青玉1個が入っている。
この中から同時に2個とり出すとき。2個とも赤玉である確率を求めよ。
食塩水苦手な人見て!

【中学数学】円周角の定理の練習問題~基礎をしっかり~【中3数学】
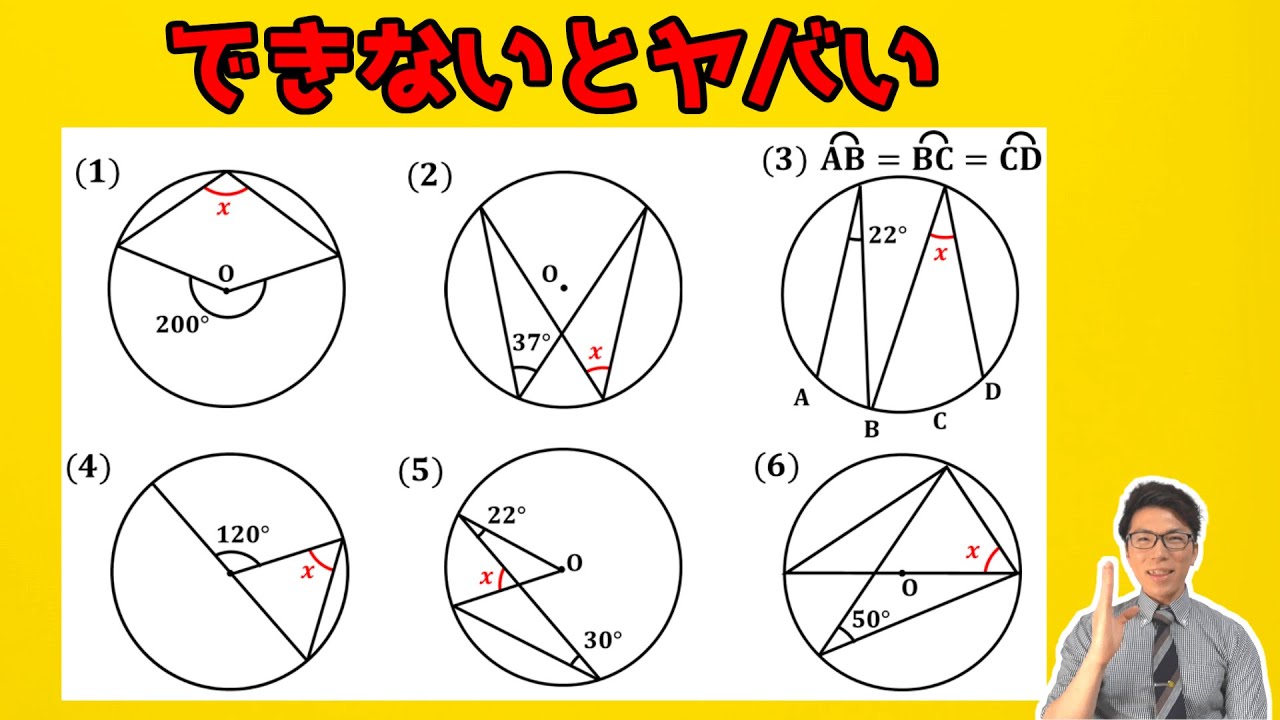
最後は意外と知らない技?

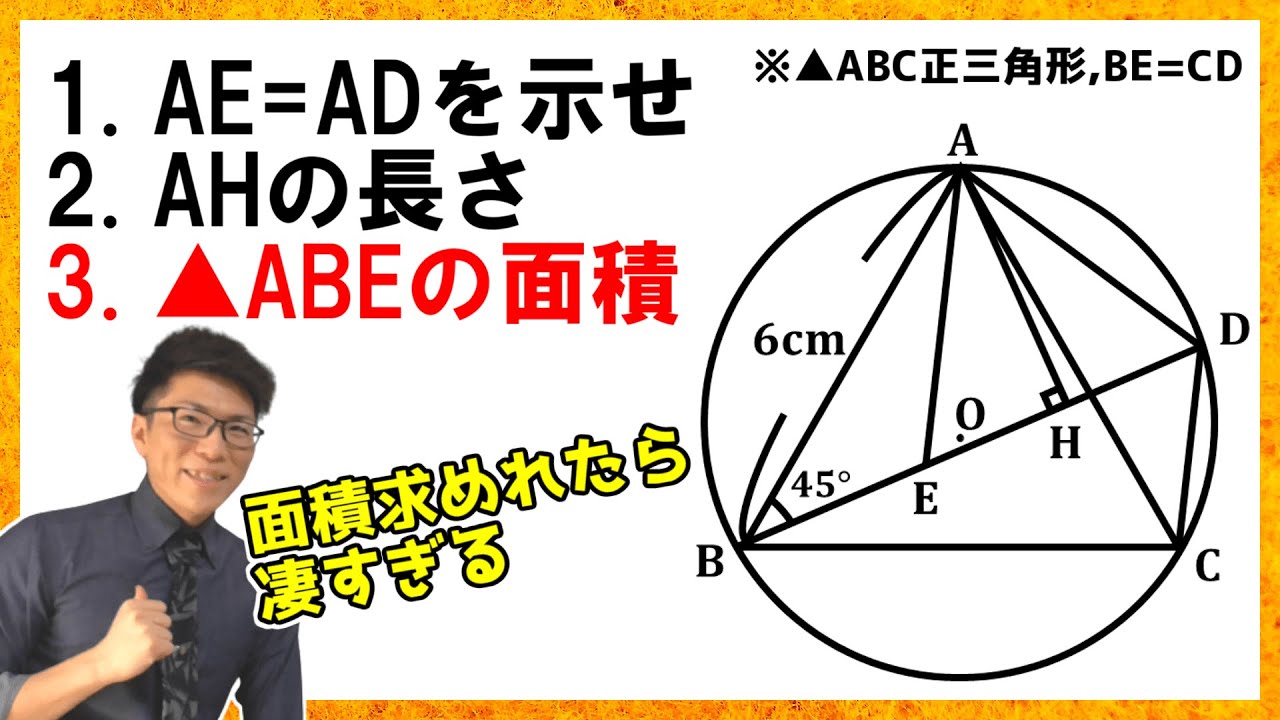
【中学数学】証明問題から三角形の面積~岐阜県公立高校入試2021年度~【高校受験】
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
4点$A,B,C,D$は円$O$の周上の点であり、$\triangle ABC$は正三角形である。また、点$E$は線分$BD$上の点で$BE=CD$である。
(1) $AE=AD$であることを証明せよ。
(2) 点$A$から線分$BD$にひいた垂線と$BD$との交点を$H$とする。$AB=6\,\rm{cm},~\angle ABD=45°$のとき、
(ア) $AH$の長さを求めよ。
(イ) $\triangle ABE$の面積を求めよ。
この動画を見る
4点$A,B,C,D$は円$O$の周上の点であり、$\triangle ABC$は正三角形である。また、点$E$は線分$BD$上の点で$BE=CD$である。
(1) $AE=AD$であることを証明せよ。
(2) 点$A$から線分$BD$にひいた垂線と$BD$との交点を$H$とする。$AB=6\,\rm{cm},~\angle ABD=45°$のとき、
(ア) $AH$の長さを求めよ。
(イ) $\triangle ABE$の面積を求めよ。
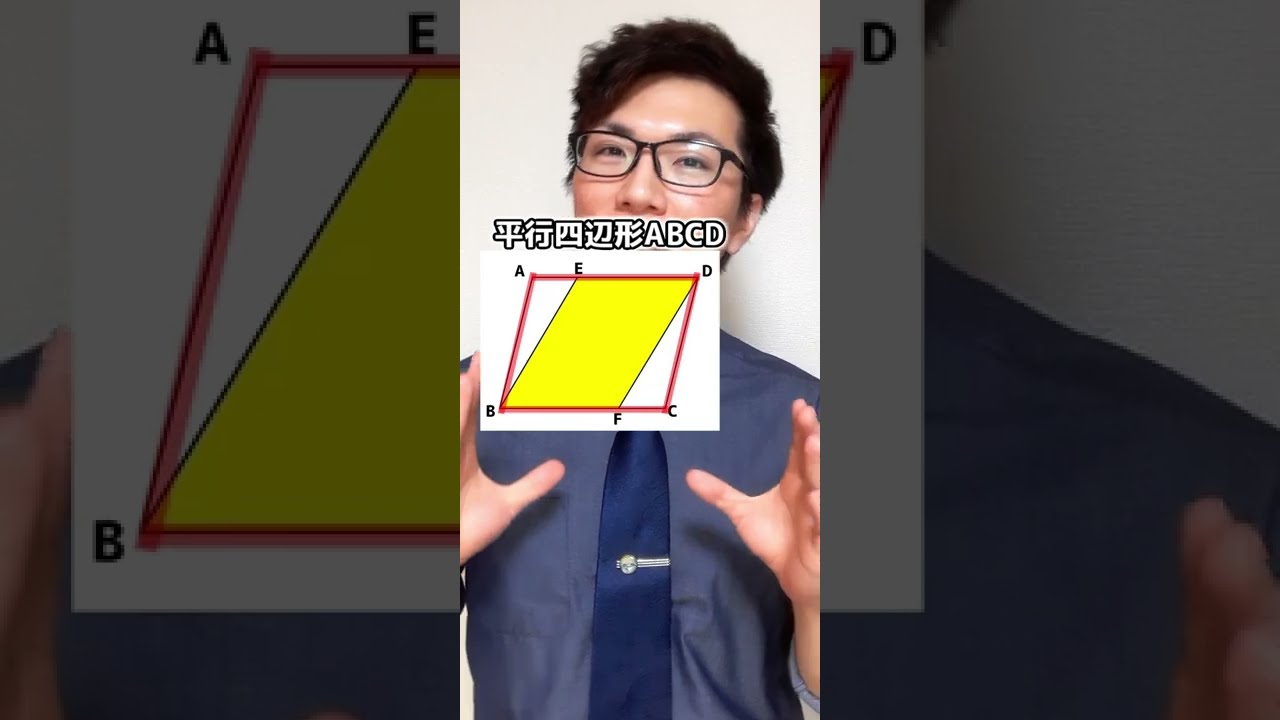
平行四辺形の証明できる?
【中学数学】確率の裏技~取り扱い注意ね~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
この動画を見る
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
【中学数学】2次方程式の解き方まとめ 3-6【中3数学】

解ける?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
233x+267y=400 \\
267x+233y=100
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
233x+267y=400 \\
267x+233y=100
\end{array}
\right.
\end{eqnarray}$
【裏技】池を回って追いこす系
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周720mの池がある。
Aは40m/分、Bは10m/分で同時に同じ方向へ池に沿って走る。
AがBに追いつくのは 何分後か?
この動画を見る
1周720mの池がある。
Aは40m/分、Bは10m/分で同時に同じ方向へ池に沿って走る。
AがBに追いつくのは 何分後か?
極限ってこういうこと?
【中学数学】確率の基礎~袋の問題まとめ~【中2数学】

単元:
#数学(中学生)#中2数学#確率
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
この動画を見る
(1) 袋の中に赤玉が2個、白玉が1個、青玉が1個入っている。この袋から同時に2個取り出すとき、2個とも赤玉である確率を求めよ。
(2) 袋の中に赤玉が4個、白玉が2個入っている。この袋から同時に2個取り出すとき、赤玉と白玉が1つずつ取り出される確率を求めよ。
(3) 袋の中に赤、白、青の玉がそれぞれ2個入っている。1回取り出した玉を袋に戻して、2回目を取り出すとき、取り出した2つの玉がどちらも青である確率を求めよ。
(4) 袋の中に赤玉4個、白玉2個が入っている。この袋から2個同時に取り出すとき、少なくとも1個は白玉が取り出される確率を求めよ。
1=0.999...らしい

食塩水の濃度の必勝法

過去問から問題は出ない??~過去問の使い方~

なんで円の面積は半径×半径×π?

池を反対方向に回る問題

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1周960mの池をA、Bが池に沿って反対方向に進む。
Aは70m/分、Bは50m/分のとき何分後に出会うか?
この動画を見る
1周960mの池をA、Bが池に沿って反対方向に進む。
Aは70m/分、Bは50m/分のとき何分後に出会うか?
【裏技】これ知ってる?

【中学数学】円周角の定理のまとめ~基礎固め~【中3数学】

単元:
#数学(中学生)#中3数学#円
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1つの弧に対する円周角は中心角の半分の大きさ $\angle APB=\frac{1}{2}2\angle AOB~\angle AOB=2\angle APB$
1つの弧に対する円周角の大きさは等しい$\angle APB=\angle AQB$
弧の長さが等しい⇔円周角が等しい$\stackrel{\frown}{AB}=\stackrel{\frown}{AB}~\angle APB=\angle CQD$
線分$AB$が直径$\angle APB=90°$
この動画を見る
1つの弧に対する円周角は中心角の半分の大きさ $\angle APB=\frac{1}{2}2\angle AOB~\angle AOB=2\angle APB$
1つの弧に対する円周角の大きさは等しい$\angle APB=\angle AQB$
弧の長さが等しい⇔円周角が等しい$\stackrel{\frown}{AB}=\stackrel{\frown}{AB}~\angle APB=\angle CQD$
線分$AB$が直径$\angle APB=90°$
これは知らないと損すぎる

【中学数学】因数分解のテクニックまとめ 3-4【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\,6x^2y-15xy^2+27xy$
$\displaystyle
(2)\,x^2+x-56$
$\displaystyle
(3)\,x^2-18x+81$
$\displaystyle
(4)\,4x^2+20x+25$
$\displaystyle
(5)\,4x^2-81$
$\displaystyle
(6)\,9(a+B)^2-30(a+b)+16$
$\displaystyle
(7)\,6x^2+12x-48$
$\displaystyle
(8)\,ax+ay-5x-5y$
$\displaystyle
(9)\,x^2+6xy+9y^2-4a^2$
$\displaystyle
(10)\,1-x^2+8xy-16y^2$
この動画を見る
$\displaystyle
(1)\,6x^2y-15xy^2+27xy$
$\displaystyle
(2)\,x^2+x-56$
$\displaystyle
(3)\,x^2-18x+81$
$\displaystyle
(4)\,4x^2+20x+25$
$\displaystyle
(5)\,4x^2-81$
$\displaystyle
(6)\,9(a+B)^2-30(a+b)+16$
$\displaystyle
(7)\,6x^2+12x-48$
$\displaystyle
(8)\,ax+ay-5x-5y$
$\displaystyle
(9)\,x^2+6xy+9y^2-4a^2$
$\displaystyle
(10)\,1-x^2+8xy-16y^2$
球の表面積ってなんで4πr^2?

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
球の表面積が$4 \pi r ^ 2$になるのはなぜか、理由解説動画です
この動画を見る
球の表面積が$4 \pi r ^ 2$になるのはなぜか、理由解説動画です
これ解ける?

単元:
#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$3x-5y=4$のとき$\displaystyle \frac{27^{ x }}{243^{ y }}$を求めよ
この動画を見る
$3x-5y=4$のとき$\displaystyle \frac{27^{ x }}{243^{ y }}$を求めよ
【裏技】暗算で円錐の表面積

【高校数学】時間内で誰ができるねん~共通テスト数学ⅠA第4問解説~【大学受験】

単元:
#数A#大学入試過去問(数学)#整数の性質#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(4) $11^4$を$2^4$で割ったときの余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、$x$が正の整数で最小になるのは、$x=$テト, $y=$ナニヌネノである
この動画を見る
(4) $11^4$を$2^4$で割ったときの余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、$x$が正の整数で最小になるのは、$x=$テト, $y=$ナニヌネノである




