 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学329〜商が平方数となる正の整数の個数と総和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\frac{13!}{m}$が平方数となる正の整数mの個数と総和を求めて下さい。
この動画を見る
$\frac{13!}{m}$が平方数となる正の整数mの個数と総和を求めて下さい。
福田のおもしろ数学328〜多項式の性質を繰り返し用いて多項式を求める

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理
指導講師:
福田次郎
問題文全文(内容文):
実数係数の多項式$P(x)$が任意の実数$\theta$に対して$P(\cos \theta +\sin \theta)=P(\cos \theta -\sin \theta)$を満たすとき、$P(x)=a_0+a_1 (1-x^2)^2+a_2 (1-x^2)^4 +\cdots+a_n (1-x^2)^{2n}$であることを証明して下さい。($a_0 ,a_1 ,\cdots ,a_n$は実数、$n$は0以上の整数)
この動画を見る
実数係数の多項式$P(x)$が任意の実数$\theta$に対して$P(\cos \theta +\sin \theta)=P(\cos \theta -\sin \theta)$を満たすとき、$P(x)=a_0+a_1 (1-x^2)^2+a_2 (1-x^2)^4 +\cdots+a_n (1-x^2)^{2n}$であることを証明して下さい。($a_0 ,a_1 ,\cdots ,a_n$は実数、$n$は0以上の整数)
福田のおもしろ数学327〜自然数の集合が和の等しい2つの集合に分割できる条件

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\mathit{X}_n ={1, 2, 3, \cdots ,n}$とする。この$\mathit{X}_n$を合計が等しい2つの集合に分割できるような自然数$n$の値をすべて求めよ。
この動画を見る
$\mathit{X}_n ={1, 2, 3, \cdots ,n}$とする。この$\mathit{X}_n$を合計が等しい2つの集合に分割できるような自然数$n$の値をすべて求めよ。
福田のおもしろ数学326〜三角形の内接円の半径

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
図のように半径34の円が8個、△ABCの辺BCに接しながら一列に外接しながら並んでいる。両端の円はそれぞれ辺AB、ACに接する。同じように半径1の円を並べると2022個並んだ。このとき、△ABCの内接円の半径を求めよ。
この動画を見る
図のように半径34の円が8個、△ABCの辺BCに接しながら一列に外接しながら並んでいる。両端の円はそれぞれ辺AB、ACに接する。同じように半径1の円を並べると2022個並んだ。このとき、△ABCの内接円の半径を求めよ。
福田のおもしろ数学325〜不定方程式の自然数解の個数

単元:
#数Ⅱ#式と証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$a,b,nは正の整数とする。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{n}$$
$$を満たす(a,b)の組の個数が2017であるとき$$
$$nが平方数であることを示せ。$$
この動画を見る
$$a,b,nは正の整数とする。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{n}$$
$$を満たす(a,b)の組の個数が2017であるとき$$
$$nが平方数であることを示せ。$$
福田のおもしろ数学324〜条件を満たす素数を調べる

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$p+2,p+6,p+8,p+12,p+14$がすべて素数になるような素数$p$をすべて求めよ。
$q+2,q+6,q+8,q+12$がすべて素数になるような素数qが$200$以下の自然数の中に少なくとも3個あることを示せ。
この動画を見る
$p+2,p+6,p+8,p+12,p+14$がすべて素数になるような素数$p$をすべて求めよ。
$q+2,q+6,q+8,q+12$がすべて素数になるような素数qが$200$以下の自然数の中に少なくとも3個あることを示せ。
福田のおもしろ数学323〜小数部分の和を不等式で評価する

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
この動画を見る
$x$の小数部分を$\{x\}$で表すことにする。
$\displaystyle\{\sqrt{1}\}+\{\sqrt{2}\}+\{\sqrt{3}\}+・・・+\{\sqrt{n^2}\}\leqq \frac{n^2-1}{2}$
を証明せよ。
福田のおもしろ数学322〜有限個の点の集合の性質

単元:
#数A#図形の性質
指導講師:
福田次郎
問題文全文(内容文):
「どの3点A,B,Cを選んでも、△ABCの面積は1未満である」
という性質を持つ平面上の有限個の点がある。
これらすべての点を、周および内部に含むような、面積4未満の三角形が存在することを証明せよ。
この動画を見る
「どの3点A,B,Cを選んでも、△ABCの面積は1未満である」
という性質を持つ平面上の有限個の点がある。
これらすべての点を、周および内部に含むような、面積4未満の三角形が存在することを証明せよ。
福田のおもしろ数学321〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x^2+y^2+z^2=2xyz$ を満たす整数の組 $(x,y,z)$ は $(0,0,0)$ のみであることを示してください。
この動画を見る
$x^2+y^2+z^2=2xyz$ を満たす整数の組 $(x,y,z)$ は $(0,0,0)$ のみであることを示してください。
福田のおもしろ数学320〜完全平方数となる条件

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
自然数 $n$ に対して $n \cdot 2^n +1$ が平方数となるような $n$ をすべて求めて下さい。
この動画を見る
自然数 $n$ に対して $n \cdot 2^n +1$ が平方数となるような $n$ をすべて求めて下さい。
福田のおもしろ数学319〜桁数と極限

単元:
#数Ⅱ#指数関数と対数関数#対数関数#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
自然数 $n$ に対して $3^n$ の桁数を $k_n$ とするとき、$\displaystyle \lim_{n \to \infty} \frac{k_n}{n}$ を求めよ。
この動画を見る
自然数 $n$ に対して $3^n$ の桁数を $k_n$ とするとき、$\displaystyle \lim_{n \to \infty} \frac{k_n}{n}$ を求めよ。
福田のおもしろ数学318〜合成関数と関数方程式

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数から実数への関数$f(x)$がすべての実数$x$で
$f(f(x)f(1-x))=f(x)$
かつ$f(f(x))=1-f(x)$を満たす。
このような$f(x)$をすべて求めて下さい。
この動画を見る
実数から実数への関数$f(x)$がすべての実数$x$で
$f(f(x)f(1-x))=f(x)$
かつ$f(f(x))=1-f(x)$を満たす。
このような$f(x)$をすべて求めて下さい。
福田の数学〜北里大学2024医学部第3問〜確率漸化式

単元:
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
箱Aには赤玉2個、白玉1個入っており、箱Bには白玉3個が入っている。2つの箱A、Bについて、次の操作を繰り返す。
(操作)2つの箱A,Bからそれぞれ1個ずつ玉を同時に取り出し、箱Aから取り出した玉を箱Bに入れて、箱Bから取り出した玉を箱Aに入れる。
n回目の操作を終えたときに箱Aに入っている赤玉の個数が2個、1個、0個である確率をそれぞれ$p_n,q_n,r_n$とする。
(1)$p_1,q_1,p_2,q_2$を求め、$r_n$を$p_n$と$q_n$を用いて表せ。
(2)$p_{n+1}$を$p_n,q_n$で表せ。また$q_{n+1}$を$q_n$を用いて表せ。
(3)$q_n$を求めよ。
(4)$s_n=3^np_n$とおいて、$s_n$を求めよ。また、$p_n$を求めよ。
この動画を見る
箱Aには赤玉2個、白玉1個入っており、箱Bには白玉3個が入っている。2つの箱A、Bについて、次の操作を繰り返す。
(操作)2つの箱A,Bからそれぞれ1個ずつ玉を同時に取り出し、箱Aから取り出した玉を箱Bに入れて、箱Bから取り出した玉を箱Aに入れる。
n回目の操作を終えたときに箱Aに入っている赤玉の個数が2個、1個、0個である確率をそれぞれ$p_n,q_n,r_n$とする。
(1)$p_1,q_1,p_2,q_2$を求め、$r_n$を$p_n$と$q_n$を用いて表せ。
(2)$p_{n+1}$を$p_n,q_n$で表せ。また$q_{n+1}$を$q_n$を用いて表せ。
(3)$q_n$を求めよ。
(4)$s_n=3^np_n$とおいて、$s_n$を求めよ。また、$p_n$を求めよ。
福田のおもしろ数学317〜複雑な数列の極限

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle a_n=n\log n\log(n+1)\{\sin(\frac{1}{\log n})-\sin(\frac{1}{\log(n+1})\}$
$\displaystyle \lim_{n\to \infty}a_n$を求めて下さい。
この動画を見る
$\displaystyle a_n=n\log n\log(n+1)\{\sin(\frac{1}{\log n})-\sin(\frac{1}{\log(n+1})\}$
$\displaystyle \lim_{n\to \infty}a_n$を求めて下さい。
福田の数学〜北里大学2024医学部第2問〜関数と不等式の証明

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)関数$y=\frac{1}{x}$の定積分を用いて、$n\geqq 2$を満たすすべての$n$に対して$f(x)\gt 0$が成り立つことを示せ。
(2)$f(x)=x+\frac{x}{1+x}-2\log (1+x)$とおく。すべての正の実数$x$に対して、$f(x)\gt 0$が成り立つことを証明せよ。さらに、すべての正の整数$n$に対して$\frac{1}{n}+\frac{1}{n+1}\gt 2\log (1+\frac{1}{n})$を示せ。
(3)$n\geqq 2$を満たすすべての整数$n$に対して$\displaystyle \sum_{k=1}^n \frac{1}{k}-\frac{1}{2}(1+\frac{1}{n})\gt \log n$が成り立つことを証明せよ。
この動画を見る
(1)関数$y=\frac{1}{x}$の定積分を用いて、$n\geqq 2$を満たすすべての$n$に対して$f(x)\gt 0$が成り立つことを示せ。
(2)$f(x)=x+\frac{x}{1+x}-2\log (1+x)$とおく。すべての正の実数$x$に対して、$f(x)\gt 0$が成り立つことを証明せよ。さらに、すべての正の整数$n$に対して$\frac{1}{n}+\frac{1}{n+1}\gt 2\log (1+\frac{1}{n})$を示せ。
(3)$n\geqq 2$を満たすすべての整数$n$に対して$\displaystyle \sum_{k=1}^n \frac{1}{k}-\frac{1}{2}(1+\frac{1}{n})\gt \log n$が成り立つことを証明せよ。
福田のおもしろ数学316〜x^n+x^{-n}が整数である証明と倍数

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
この動画を見る
2より大きい整数$t$に対して$t=x+x^{-1}$を満たす実数$x$を考える。$t_n = x+x^{-n}$とするとき$t_n$は常に整数であることを示せ。また、$t_n$が$t$の倍数となるような正の整数$n$をすべて求めよ。
福田の数学〜北里大学2024医学部第1問(4)〜正の約数の個数と総和

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2052の正の約数は全部で$\fbox{コ}$個あり、2052の正の約数の総和は$\fbox{サ}$である。また、300以下の正の整数のうち、正の約数の個数が偶数であるものは全部で$\fbox{シ}$個ある。
この動画を見る
2052の正の約数は全部で$\fbox{コ}$個あり、2052の正の約数の総和は$\fbox{サ}$である。また、300以下の正の整数のうち、正の約数の個数が偶数であるものは全部で$\fbox{シ}$個ある。
福田のおもしろ数学315〜不定方程式の整数解

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x^3 +y^3 +z^3 -3xyz=2003$を満たす整数$x, y, z$をすべて求めよ。
この動画を見る
$x^3 +y^3 +z^3 -3xyz=2003$を満たす整数$x, y, z$をすべて求めよ。
福田の数学〜北里大学2024医学部第1問(3)〜空間ベクトルと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
座標空間に4点A(-1, -1, -1), B(2, 0, 1), C(-2, 2, 0), D(1,0,5)がある。このとき、三角形ABCの面積は キ である。平面ABC上に点Hを直線DHが平面 ABCと垂直になるようにとると、点Hの座標は ク である。また、四面体ABCD の体積は ケ である。
この動画を見る
座標空間に4点A(-1, -1, -1), B(2, 0, 1), C(-2, 2, 0), D(1,0,5)がある。このとき、三角形ABCの面積は キ である。平面ABC上に点Hを直線DHが平面 ABCと垂直になるようにとると、点Hの座標は ク である。また、四面体ABCD の体積は ケ である。
福田のおもしろ数学314〜条件付き循環形式の不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師:
福田次郎
問題文全文(内容文):
$abc=1$を満たす正の数$a, b, c$に対して$\frac{ab}{a^5+b^5+ab}+\frac{bc}{b^5+c^5+bc}+\frac{ca}{c^5+a^5+ca}\leqq 1$であることを示せ。
この動画を見る
$abc=1$を満たす正の数$a, b, c$に対して$\frac{ab}{a^5+b^5+ab}+\frac{bc}{b^5+c^5+bc}+\frac{ca}{c^5+a^5+ca}\leqq 1$であることを示せ。
福田の数学〜北里大学2024医学部第1問(2)〜定積分で表された関数の最小値

単元:
#大学入試過去問(数学)#積分とその応用#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(2) $0\leqq x\leqq 2\pi$において、曲線$y=\sin x$と$x$軸で囲まれた2つの部分の面積の和は$\fbox{エ}$である。
$0\leqq x\leqq 2\pi$において、曲線$y=\sin x$と曲線$y= \cos x$ で囲まれた部分の面積は$\fbox{オ}$である。また、$f(x) =\displaystyle \int_{x}^{ x+\frac{\pi}{2} } |\sin t|dt $とすると、関数$f(x)$の最小値は$\fbox{カ}$である。
この動画を見る
(2) $0\leqq x\leqq 2\pi$において、曲線$y=\sin x$と$x$軸で囲まれた2つの部分の面積の和は$\fbox{エ}$である。
$0\leqq x\leqq 2\pi$において、曲線$y=\sin x$と曲線$y= \cos x$ で囲まれた部分の面積は$\fbox{オ}$である。また、$f(x) =\displaystyle \int_{x}^{ x+\frac{\pi}{2} } |\sin t|dt $とすると、関数$f(x)$の最小値は$\fbox{カ}$である。
福田のおもしろ数学313〜1分チャレンジ!数値の計算です

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\frac{2025^4 + 4\times 2024^4}{2024^2+4049^2}-\frac{2023^4+4\times 2024^2}{2024^2+4047^2}$ を計算してください。
この動画を見る
$\frac{2025^4 + 4\times 2024^4}{2024^2+4049^2}-\frac{2023^4+4\times 2024^2}{2024^2+4047^2}$ を計算してください。
福田の数学〜北里大学2024医学部第1問(1)〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
この動画を見る
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
福田のおもしろ数学312〜三角形の内角と辺の長さに成り立つ不等式の証明

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\triangle $ABCにおいて$60 \leqq \frac{aA+bB+cC}{a+b+c} \lt 90$が成り立つことを証明してください。ただし、A,B,Cは度数法で表されているものとする。
この動画を見る
$\triangle $ABCにおいて$60 \leqq \frac{aA+bB+cC}{a+b+c} \lt 90$が成り立つことを証明してください。ただし、A,B,Cは度数法で表されているものとする。
福田の数学〜早稲田大学2024社会科学部第3問〜集合と数列

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
この動画を見る
$n$を$n \geqq 3$である自然数とする。相異なる$n$個の正の数を小さい順に並べた集合$S=${ $a_{ 1 },a_{ 2 }・・・,a_{ n } $}を考える。$a_{ 1 }=k$とするとき、次の問いに答えよ。
(1)$a_{ i }-a_{ 1 }$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ 2 }$を求めよ。
(2)(1)のとき、$a_{ n }$を$n$の式で表せ。
(3)$\frac{a_{ i }}{a_{ 1 }}$$(i=2,3,・・・,n)$がすべての$S$の要素となるとき、$a_{ n }$を$n$の式で表せ。
福田のおもしろ数学311〜n個の積の和を最大にする方法

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$n$個の実数 $a_1\leqq a_2\leqq \cdots \leqq a_n$と$n$個の実数を適当に並べたものを$b_1, b_2, \cdots ,b_n $ として、$s = a_1b_1+a_2b_2+\cdots + a_nb_n $を最大にするには$b_1 \leqq b_2 \leqq \cdots \leqq b_n $となるように並べたときである。これを証明して下さい。(ただし、$n\geqq 2$とする)
この動画を見る
$n$個の実数 $a_1\leqq a_2\leqq \cdots \leqq a_n$と$n$個の実数を適当に並べたものを$b_1, b_2, \cdots ,b_n $ として、$s = a_1b_1+a_2b_2+\cdots + a_nb_n $を最大にするには$b_1 \leqq b_2 \leqq \cdots \leqq b_n $となるように並べたときである。これを証明して下さい。(ただし、$n\geqq 2$とする)
福田の数学〜早稲田大学2024社会科学部第2問〜三角形の内心と垂心の位置ベクトル

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
\fcolorbox{black}{ white }{$2$}OA = 6, \,OB = 5,\,AB=7である\triangle OABにおいて、\vec{a} \ = \ \vec{OA} , \ \vec{b} \ = \ \vec{OB}とおく。
\end{eqnarray}
$
$
\begin{eqnarray}
(1)\triangle OABの内心を1、辺ABと直線OIの交点をCとする。\vec{OC}を\vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
$
\begin{eqnarray}
(1) \vec{OI}を \vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
\fcolorbox{black}{ white }{$2$}OA = 6, \,OB = 5,\,AB=7である\triangle OABにおいて、\vec{a} \ = \ \vec{OA} , \ \vec{b} \ = \ \vec{OB}とおく。
\end{eqnarray}
$
$
\begin{eqnarray}
(1)\triangle OABの内心を1、辺ABと直線OIの交点をCとする。\vec{OC}を\vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
$
\begin{eqnarray}
(1) \vec{OI}を \vec{a}, \ \vec{b}で表せ。
\end{eqnarray}
$
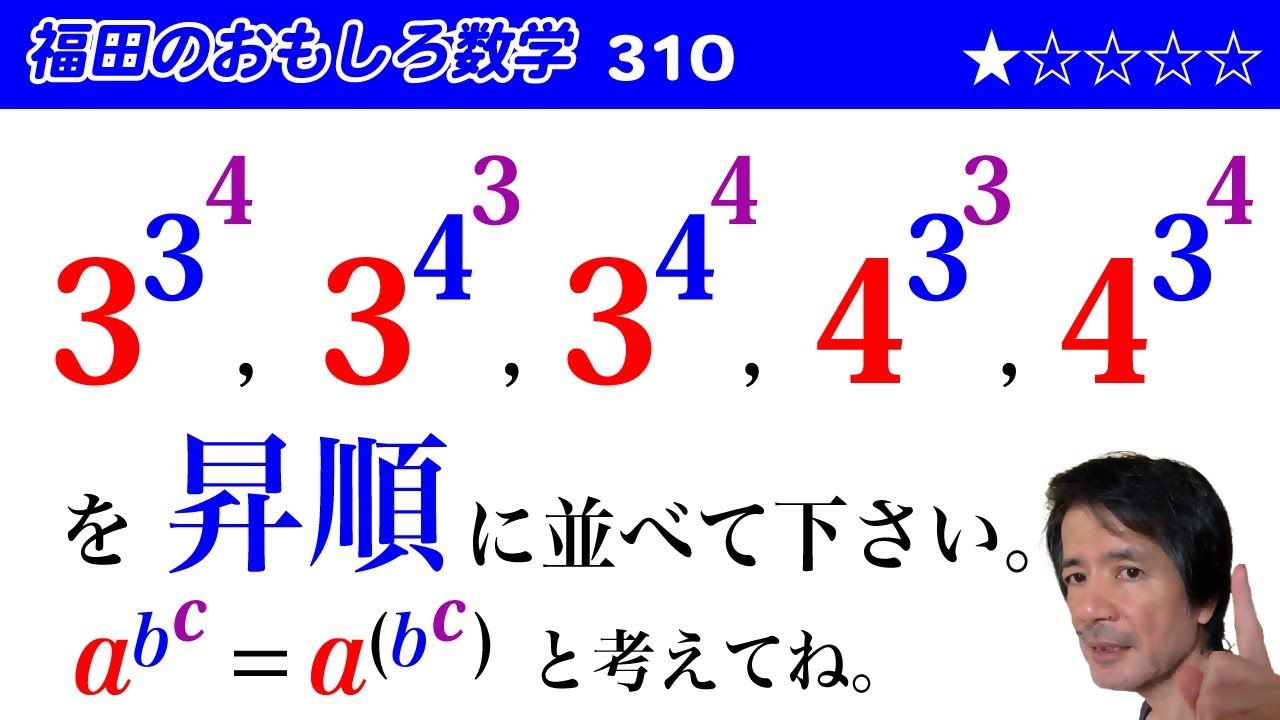
福田のおもしろ数学310〜累乗で表された数の大小比較
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$\left( \left( 3 \right)^3 \right)^4,\left( \left( 3 \right)^4 \right)^3,\left( \left( 3 \right)^4\right)^4,\left( \left( 4\right)^3 \right)^3,\left( \left( 4 \right)^3 \right)^4を昇順に直してください。ただし、a^{ b^c}=a^{ (b^c)}とする。$$
この動画を見る
$$\left( \left( 3 \right)^3 \right)^4,\left( \left( 3 \right)^4 \right)^3,\left( \left( 3 \right)^4\right)^4,\left( \left( 4\right)^3 \right)^3,\left( \left( 4 \right)^3 \right)^4を昇順に直してください。ただし、a^{ b^c}=a^{ (b^c)}とする。$$
福田の数学〜早稲田大学2024社会科学部第1問〜領域における最大最小

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$連立不等式
y≦-\frac{2}{3}x+4, y≧x-1,x≧0,y≧0
の表す領域をDとする。点(x,y)が領域Dを動くとき、次の問いに答えよ。
$$(1)領域Dを座標平面上に図示せよ。$$
$$(2)-2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(3)2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(4)aがすべての実数を動くとき、ax+yの最大値をaで分類せよ。$$
この動画を見る
$$連立不等式
y≦-\frac{2}{3}x+4, y≧x-1,x≧0,y≧0
の表す領域をDとする。点(x,y)が領域Dを動くとき、次の問いに答えよ。
$$(1)領域Dを座標平面上に図示せよ。$$
$$(2)-2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(3)2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(4)aがすべての実数を動くとき、ax+yの最大値をaで分類せよ。$$
福田のおもしろ数学309〜自然数から自然数への関数f(n)に関する関数方程式

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$$自然数を自然数へ写す関数f(n)が次を満たす。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow \frac{1}{f(a)}+\frac{1}{f(b)}=\frac{1}{f(c)}$$
$$このような関数f(n)をすべて求めて下さい。$$
この動画を見る
$$自然数を自然数へ写す関数f(n)が次を満たす。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{c}\Rightarrow \frac{1}{f(a)}+\frac{1}{f(b)}=\frac{1}{f(c)}$$
$$このような関数f(n)をすべて求めて下さい。$$



