ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
チャレンジ問題（複雑なパズル）
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{1}{1}=?,\ \dfrac{2\cdot 3}{1\cdot 3}=?,\ \dfrac{3\cdot 5\cdot 6}{1\cdot 3\cdot 5}=?$
$\dfrac{4 \cdot 7 \cdot 9 \cdot 10}{1 \cdot 3 \cdot 5 \cdot 7}=?,\ \dfrac{5 \cdot 9 \cdot 12 \cdot 14 \cdot 15}{1 \cdot 3 \cdot 5 \cdot 7 \cdot 4}=?$
(1)各式の右辺を計算せよ.
(2)式の両辺がどのように続くか予想せよ.
(3)(2)の予想を示せ.
この動画を見る
$\dfrac{1}{1}=?,\ \dfrac{2\cdot 3}{1\cdot 3}=?,\ \dfrac{3\cdot 5\cdot 6}{1\cdot 3\cdot 5}=?$
$\dfrac{4 \cdot 7 \cdot 9 \cdot 10}{1 \cdot 3 \cdot 5 \cdot 7}=?,\ \dfrac{5 \cdot 9 \cdot 12 \cdot 14 \cdot 15}{1 \cdot 3 \cdot 5 \cdot 7 \cdot 4}=?$
(1)各式の右辺を計算せよ.
(2)式の両辺がどのように続くか予想せよ.
(3)(2)の予想を示せ.
21滋賀県教員採用試験（数学：5番 接線の本数）
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
$a$は実数である.
点$(a,0)$を通る曲線
$y=(2-x)e^x$の接線の本数を求めよ.
この動画を見る
$\boxed{5}$
$a$は実数である.
点$(a,0)$を通る曲線
$y=(2-x)e^x$の接線の本数を求めよ.
高専数学 微積I #243(1) 媒介変数曲線（ｘ軸回転体）
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
この動画を見る
$-1\leqq t\leqq 1$である.
曲線$x=t^3,y=t^2-1$と$x$軸で囲まれた
図形を$x$軸中心に回転した体積$V$を求めよ.
練習問題35 数学オリンピックの問題 複素数を利用して証明してみた。
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学オリンピック#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.
この動画を見る
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.
高専数学 微積I #242(2) 媒介変数表示曲線の長さ
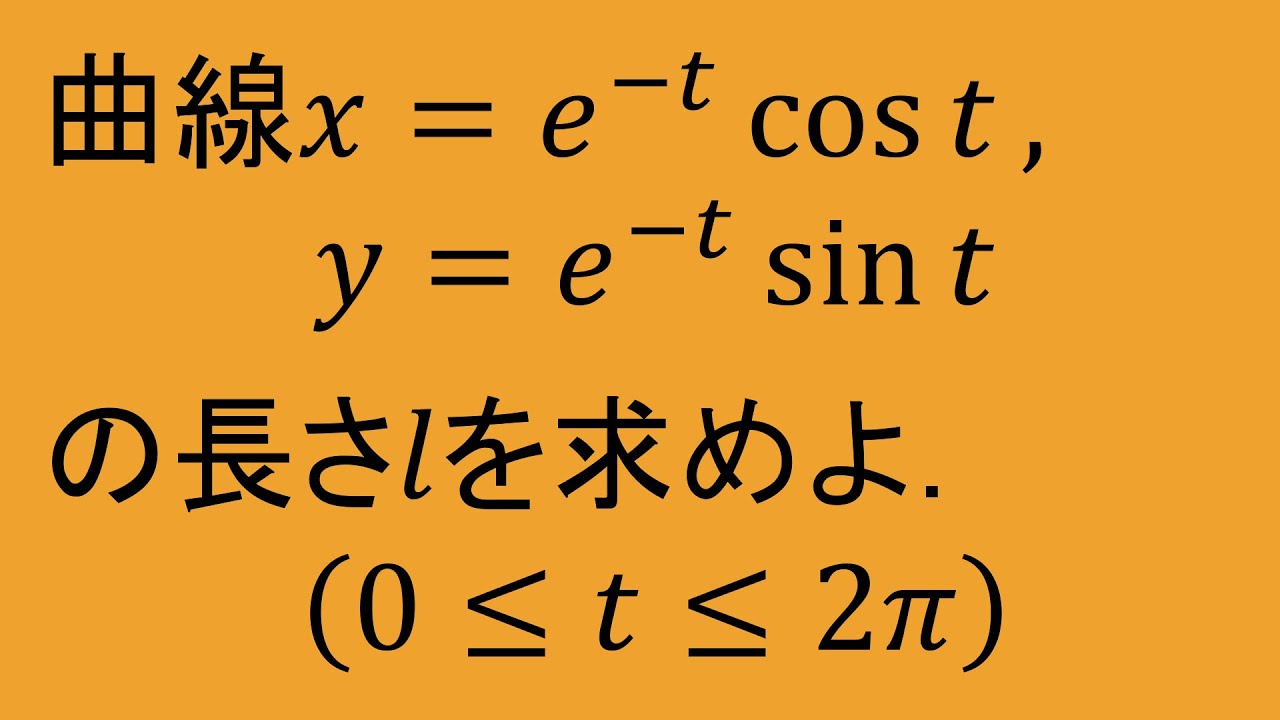
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
この動画を見る
$0\leqq t\leqq 2\pi$とする.
曲線$x=e^{-t}\cos t,y=e^{-t}\sin t$
の長さ$\ell$を求めよ.
14和歌山県教員採用試験（数学：3番 微分方程式）
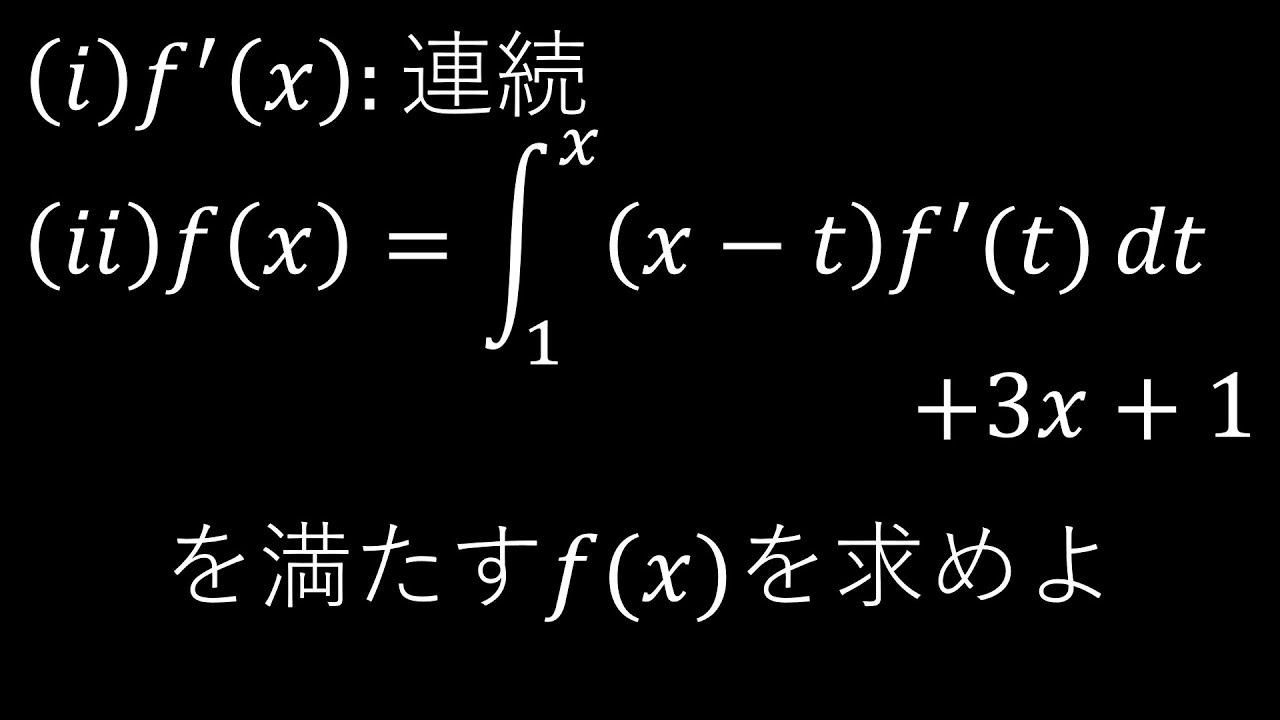
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
(i)$f`(x):$連続
(ii)$f(x)=\displaystyle \int_{1}^{x} (x-t)f`(t)dt+3x+1$
(iii)(ii)をみたす$f(x)$を求めよ.
この動画を見る
$\boxed{3}$
(i)$f`(x):$連続
(ii)$f(x)=\displaystyle \int_{1}^{x} (x-t)f`(t)dt+3x+1$
(iii)(ii)をみたす$f(x)$を求めよ.
高専数学 微積I #242(1) 媒介変数表示曲線の長さ
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
この動画を見る
曲線$x=t^3,y=3t^2(0\leqq t\leqq 1)$の
長さ$\ell$を求めよ.
練習問題34 数検1級1次 微分方程式
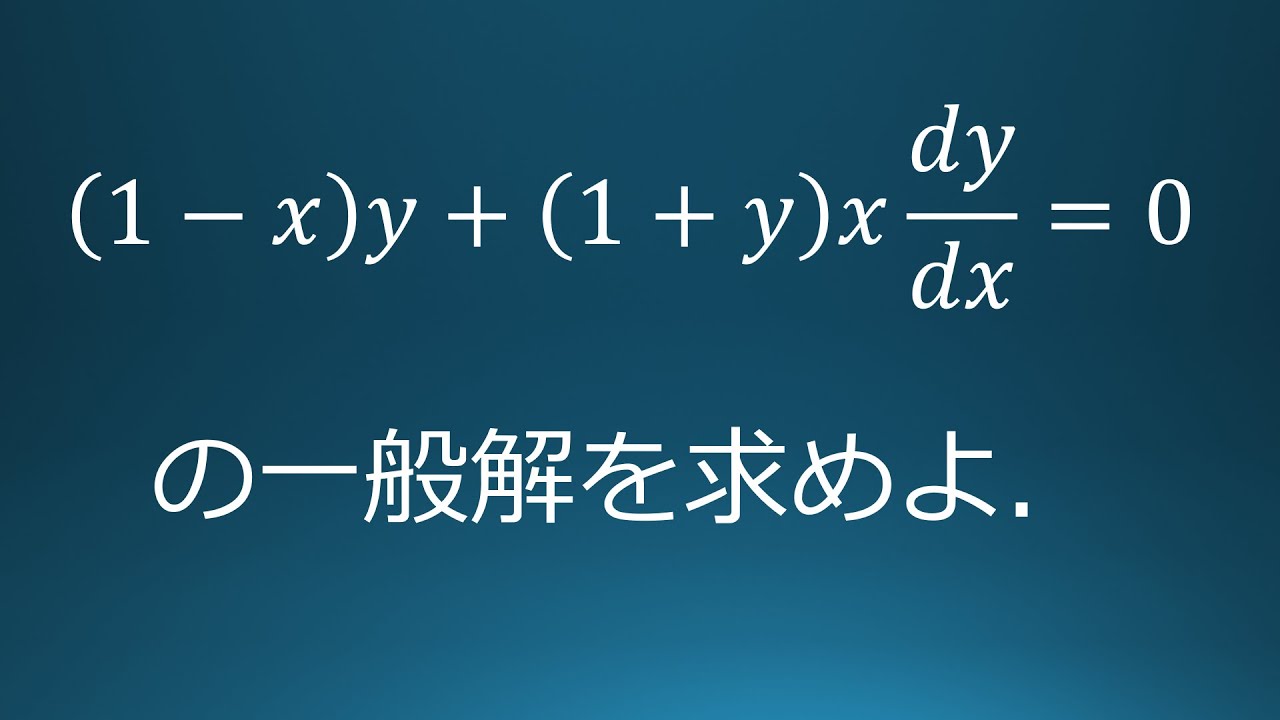
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$
の一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$
の一般解を求めよ.
高専数学 微積I #238(3)(4) 広義積分
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{\sqrt[3]{x^2}}$
(4)$\displaystyle \int_{0}^{\infty}x \ e^{-x} dx$
この動画を見る
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{\sqrt[3]{x^2}}$
(4)$\displaystyle \int_{0}^{\infty}x \ e^{-x} dx$
高専数学 微積I #238(1)(2) 広義積分
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{\infty}x^{-5} dx$
(2)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{e^{2x}}$
この動画を見る
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{\infty}x^{-5} dx$
(2)$\displaystyle \int_{0}^{\infty}\dfrac{dx}{e^{2x}}$
20滋賀県教員採用試験（数学：6番 空間ベクトル）
単元：
#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
点$A(1,2,-3)$を通り
$\vec{ a }=(3,-1,2)$に平行な直線を$\ell$とする.
点$B(4,-3,1)$を通り
$\vec{b}=(3,7,-2)$に平行な直線を$m$とする.
$\ell$と$m$の交点の座標を求めよ.
この動画を見る
$\boxed{6}$
点$A(1,2,-3)$を通り
$\vec{ a }=(3,-1,2)$に平行な直線を$\ell$とする.
点$B(4,-3,1)$を通り
$\vec{b}=(3,7,-2)$に平行な直線を$m$とする.
$\ell$と$m$の交点の座標を求めよ.
高専数学 微積I #236(3)(4) 広義積分
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{1}\dfrac{dx}{\sqrt[4]{x}}$
(4)$\displaystyle \int_{-1}^{1}\dfrac{dx}{x^4}$
この動画を見る
次の広義積分を計算せよ.
(3)$\displaystyle \int_{0}^{1}\dfrac{dx}{\sqrt[4]{x}}$
(4)$\displaystyle \int_{-1}^{1}\dfrac{dx}{x^4}$
14和歌山県教員採用試験（数学：4番 数列）
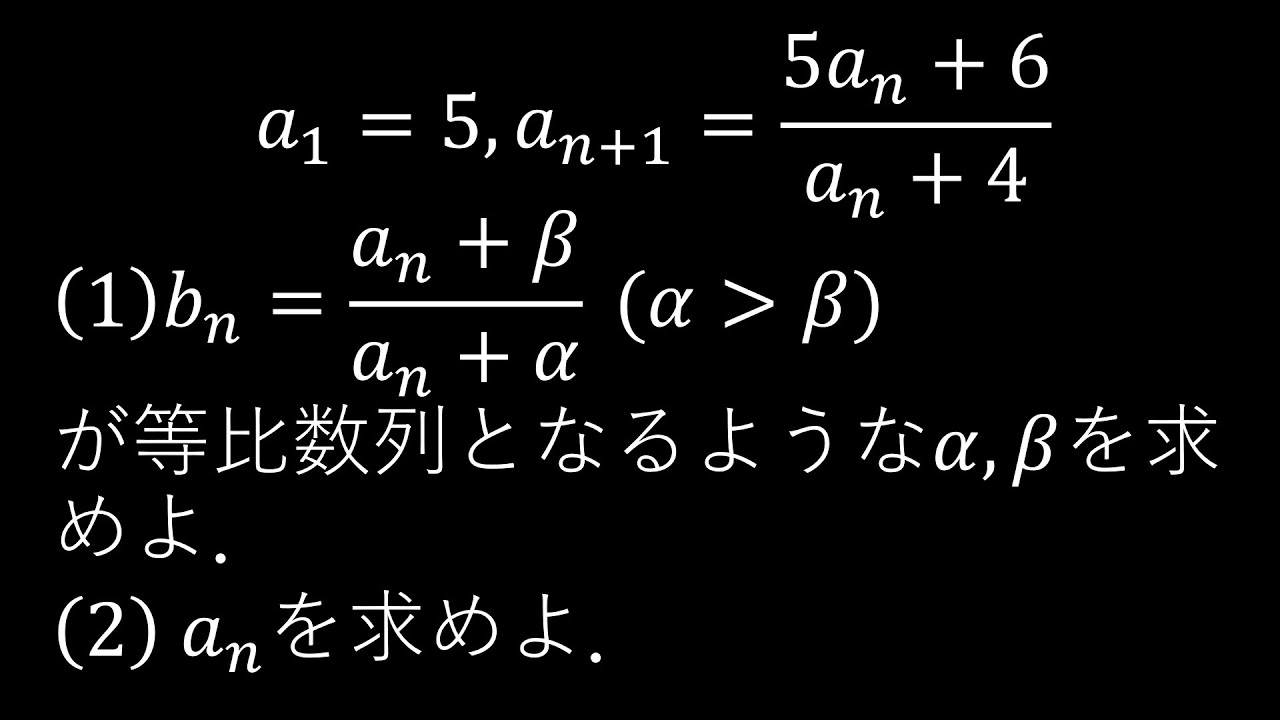
単元：
#数列#数列とその和（等差・等比・階差・Σ）#その他#数学(高校生)#数B#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$
$a_1=5,a_{n+1}=\dfrac{5a_n+6}{a_4+4}$とする.
(1)$b_n=\dfrac{a_n+\beta}{a_n+\alpha}\ (\alpha \gt \beta)$
$b_n$が等比数列となるような$\alpha,\beta$の値を求めよ.
(2)$a_n$を求めよ.
この動画を見る
$\boxed{4}$
$a_1=5,a_{n+1}=\dfrac{5a_n+6}{a_4+4}$とする.
(1)$b_n=\dfrac{a_n+\beta}{a_n+\alpha}\ (\alpha \gt \beta)$
$b_n$が等比数列となるような$\alpha,\beta$の値を求めよ.
(2)$a_n$を求めよ.
高専数学 微積I #236(1)(2) 広義積分
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{3}\dfrac{dx}{\sqrt{x-2}}$
(2)$\displaystyle \int_{0}^{3}\dfrac{dx}{\sqrt{9-x^2}}$
この動画を見る
次の広義積分を計算せよ.
(1)$\displaystyle \int_{2}^{3}\dfrac{dx}{\sqrt{x-2}}$
(2)$\displaystyle \int_{0}^{3}\dfrac{dx}{\sqrt{9-x^2}}$
12和歌山県教員採用試験（数学：1-(5) 相加・相乗平均）
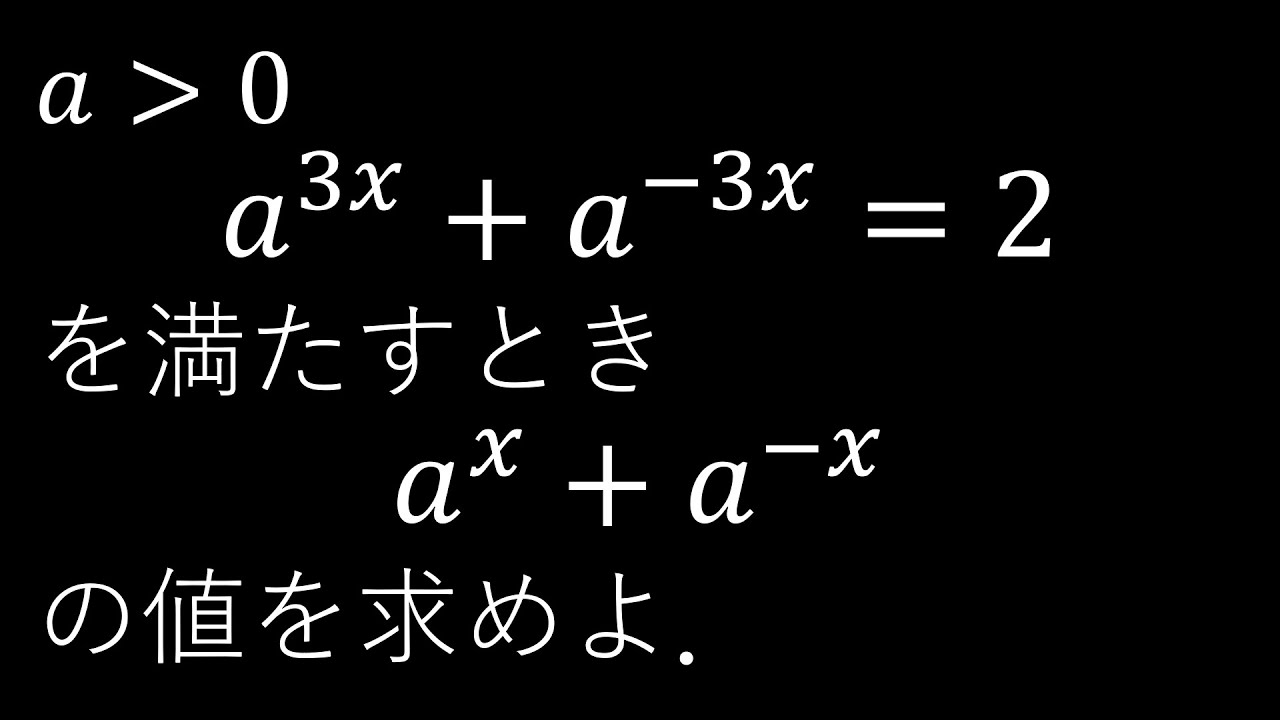
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(5)$
$a\gt 0$とする.
$a^{3x}+a^{-3x}=2$のとき,
$a^x+a^{-x}$の値を求めよ.
この動画を見る
$\boxed{1}-(5)$
$a\gt 0$とする.
$a^{3x}+a^{-3x}=2$のとき,
$a^x+a^{-x}$の値を求めよ.
17和歌山県教員採用試験（数学：1-(5) 確率）
単元：
#数A#場合の数と確率#確率#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
サイコロを3回投げ,
出た目を順に$a,b,c$とする.
$abx^2-12x+c=0$が
重解をもつ確率を求めよ.
この動画を見る
$\boxed{6}$
サイコロを3回投げ,
出た目を順に$a,b,c$とする.
$abx^2-12x+c=0$が
重解をもつ確率を求めよ.
高専数学 微積I #234(1)(2) 極座標表示の曲線の面積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
この動画を見る
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
17和歌山県教員採用試験（数学：1-(6) 展開した係数）
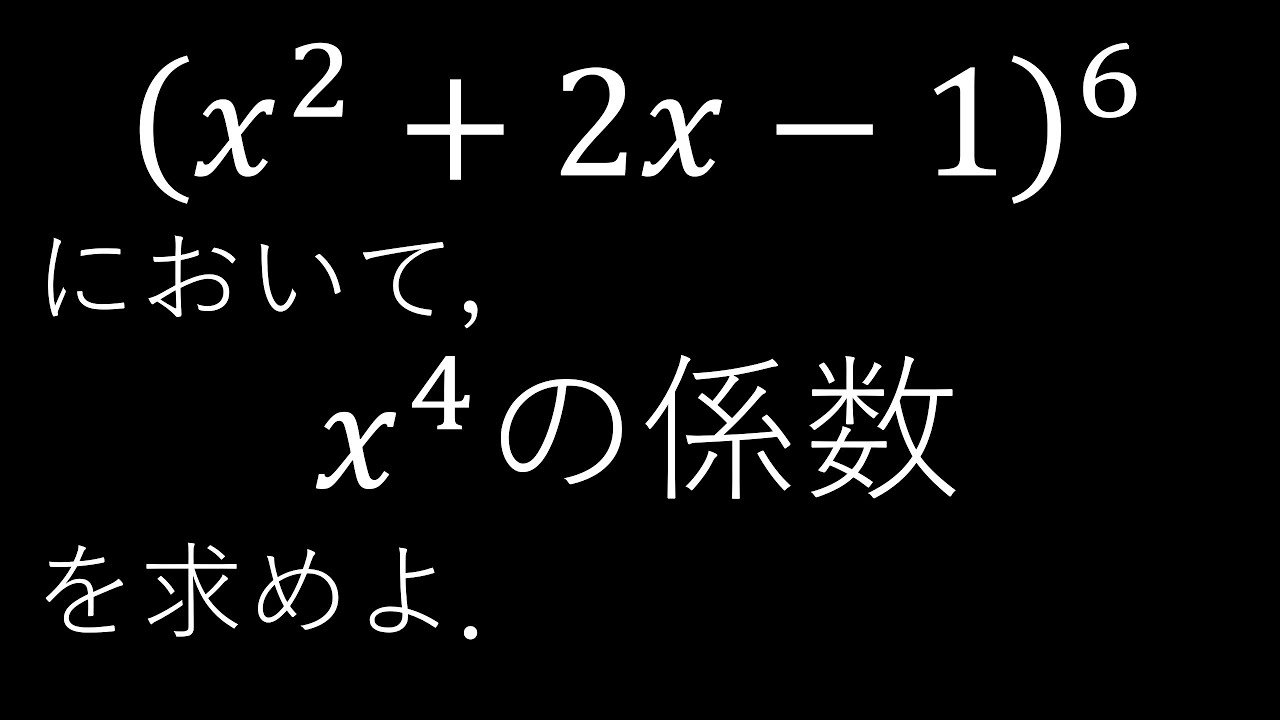
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(4)$
$(x^2+2x-1)^6$において
$x^4$の係数を求めよ.
この動画を見る
$\boxed{1}-(4)$
$(x^2+2x-1)^6$において
$x^4$の係数を求めよ.
高専数学 微積I #229(2) 媒介変数表示関数のx軸回転体の体積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
高専数学 微積I #229(1) 媒介変数表示関数のx軸回転体の体積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
11和歌山県教員採用試験（数学：4番 微分と微分方程式）
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$
$f(x)$:微分可能
任意の実数$x,y$に対して
$f(x+y)=f(x),f(y),f`(0)=2$
(1)$f(0)$を求めよ.
(2)$f(x)$を求めよ.
この動画を見る
$\boxed{4}$
$f(x)$:微分可能
任意の実数$x,y$に対して
$f(x+y)=f(x),f(y),f`(0)=2$
(1)$f(0)$を求めよ.
(2)$f(x)$を求めよ.
高専数学 微積I #227(3) 媒介変数表示関数の曲線の長さ
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
練習問題33 数検1級1次 微分方程式
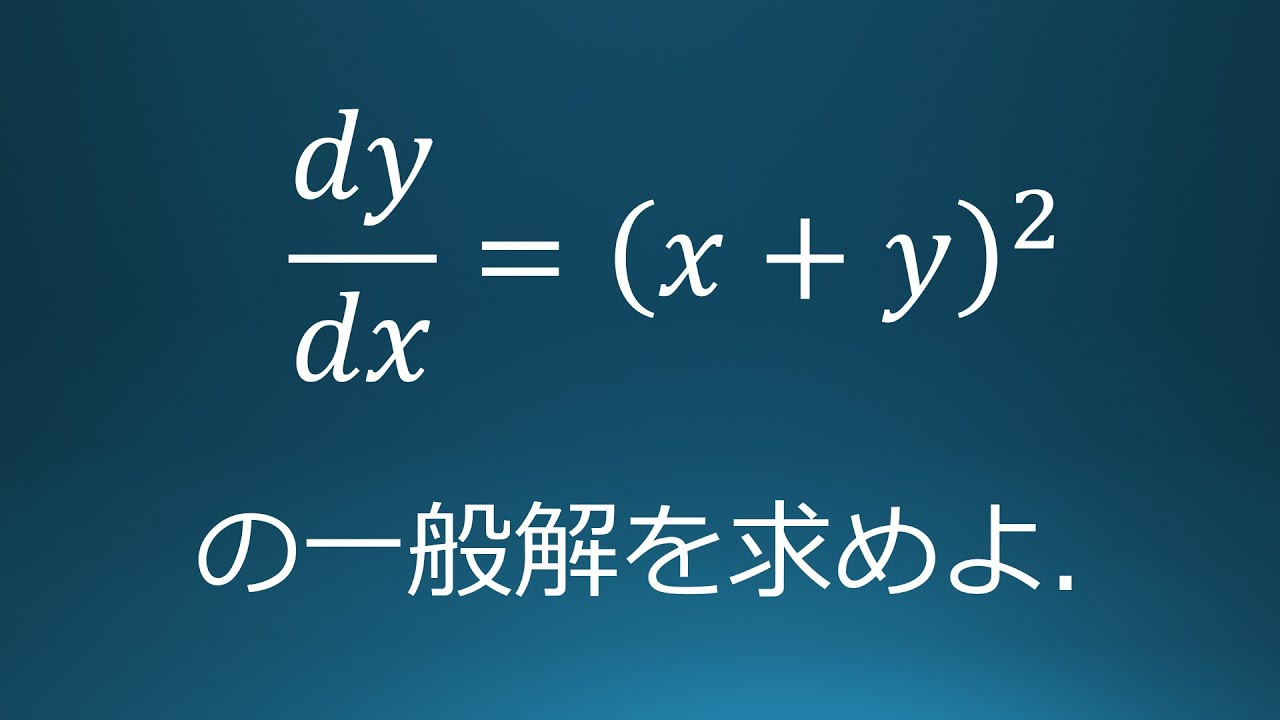
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
この動画を見る
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
08岡山県教員採用試験（数学：1-(4) 微分方程式）
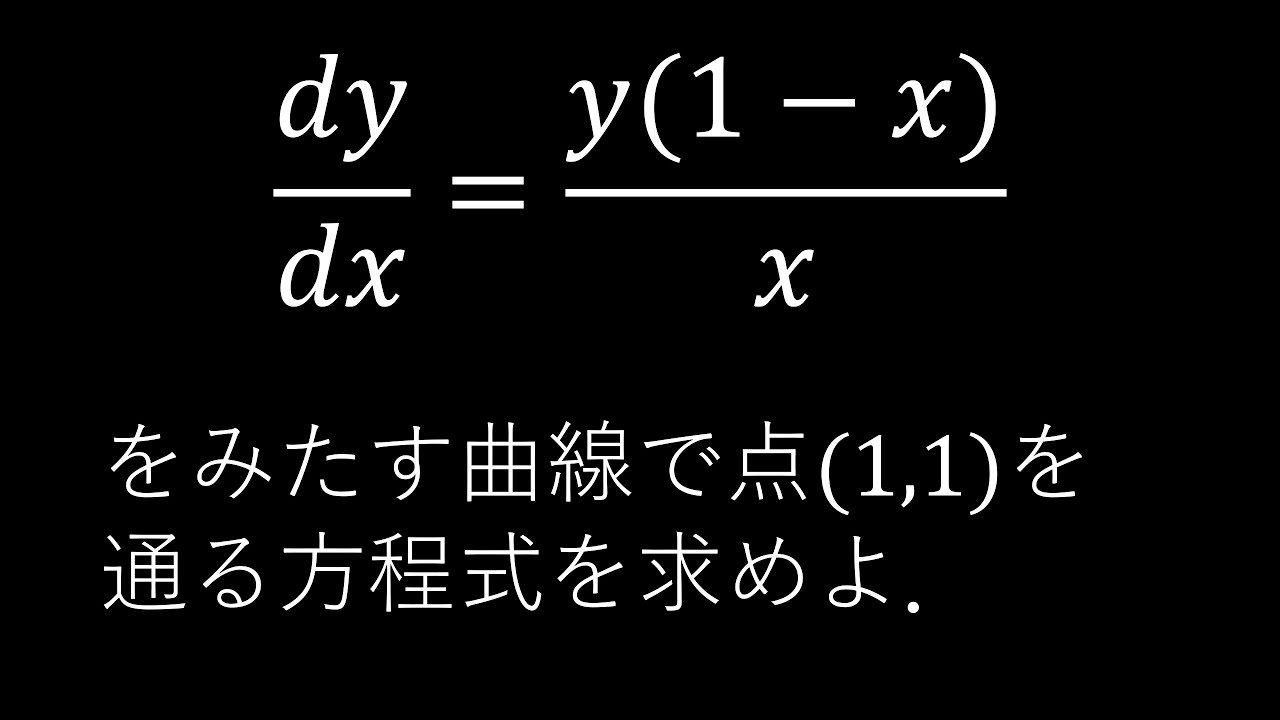
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(4)$
$\dfrac{dy}{dx}=\dfrac{y(x-1)}{x}$
をみたす曲線で$(1,1)$を通る方程式を求めよ.
この動画を見る
$\boxed{1}-(4)$
$\dfrac{dy}{dx}=\dfrac{y(x-1)}{x}$
をみたす曲線で$(1,1)$を通る方程式を求めよ.
高専数学 微積I #227(2) 媒介変数表示関数の曲線の長さ
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
16和歌山県教員採用試験（数学：4番 複素数）
単元：
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$
複素数$z=x+yi$が
$1\leqq z+\dfrac{1}{z}\leqq 6$
を満たすとき,
$z$に存在範囲を複素数平面上に図示せよ.
$x,y$は実数とする.
この動画を見る
$\boxed{4}$
複素数$z=x+yi$が
$1\leqq z+\dfrac{1}{z}\leqq 6$
を満たすとき,
$z$に存在範囲を複素数平面上に図示せよ.
$x,y$は実数とする.
高専数学 微積I #227(1) 媒介変数表示の曲線の長さ
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t \leqq \sqrt3$である.
$x=3t^2,y=3t-t^3$の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t \leqq \sqrt3$である.
$x=3t^2,y=3t-t^3$の曲線の長さ$L$を求めよ.
高専数学 微積I #226(3) 媒介変数表示の面積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
16和歌山県教員採用試験（数学：2番 解と係数の関係）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$a,b$は実数とする.
$x^3+6ax+b=0$が$a-3i$を解にもつとき,
$a,b$の値とそのときの実数解を求めよ.
この動画を見る
$\boxed{2}$
$a,b$は実数とする.
$x^3+6ax+b=0$が$a-3i$を解にもつとき,
$a,b$の値とそのときの実数解を求めよ.
ε N論法 #7 a_n ≧ b_n
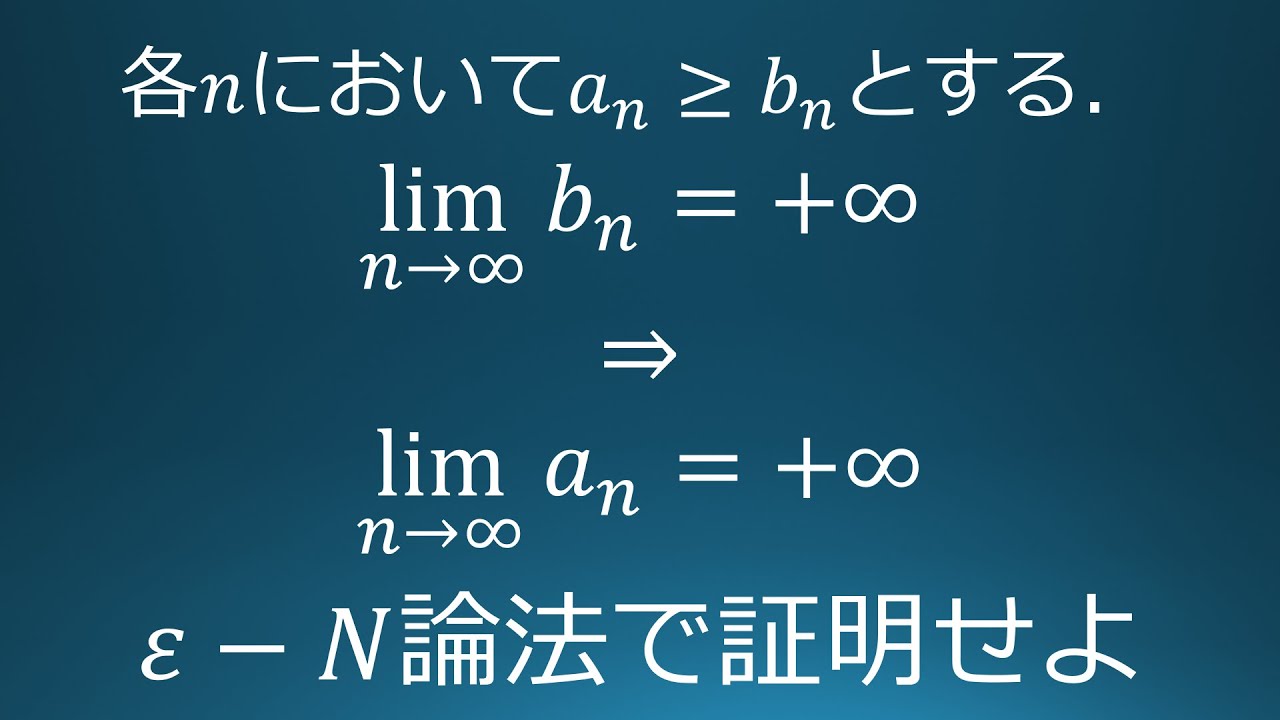
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
数列{$a_n$},{$b_n$}は各$n$において
$a_n \geqq b_n$をみたす
$\displaystyle \lim_{n\to\infty} b_n=+\infty$
$\displaystyle \lim_{n\to\infty} a_n=+\infty$
$ε N$論法で証明せよ.
この動画を見る
数列{$a_n$},{$b_n$}は各$n$において
$a_n \geqq b_n$をみたす
$\displaystyle \lim_{n\to\infty} b_n=+\infty$
$\displaystyle \lim_{n\to\infty} a_n=+\infty$
$ε N$論法で証明せよ.