 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】早稲田中2007年:図形の問題と思いきや場合の数!

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2007年早稲田中学大問2(2)の問題です。
下の図2のように、高さが6㎝の正三角形の内部の点Pから辺BC、CA、ABへ垂線を引き、その長さをそれぞれxcm、ycm、zcmとします。
x、y、zがすべて整数であるような点Pは全部で何個ありますか。
この動画を見る
2007年早稲田中学大問2(2)の問題です。
下の図2のように、高さが6㎝の正三角形の内部の点Pから辺BC、CA、ABへ垂線を引き、その長さをそれぞれxcm、ycm、zcmとします。
x、y、zがすべて整数であるような点Pは全部で何個ありますか。
【受験算数】早稲田中過去問解説:円の中の三角形の面積を求める

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2007年早稲田中学②大問2(2)です。
図2の点A、B、C、D、E、F、G、Hは半径5㎝の円の周を8等分する点です。三角形ABDの面積は何㎠ですか。
この動画を見る
2007年早稲田中学②大問2(2)です。
図2の点A、B、C、D、E、F、G、Hは半径5㎝の円の周を8等分する点です。三角形ABDの面積は何㎠ですか。
【話法シリーズ③】 自由間接話法(描出話法)

単元:
#英語(高校生)#英文法#話法の転換#大学入試過去問(英語)#学校別大学入試過去問解説(英語)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の英文を和訳しなさい。
John, now in his second year at college, was home for the spring vacation, and his mother took the opportunity of having a serious talk with him. Did he know where he wanted to live? John was not sure. Did he know what he wanted to do? He was equally uncertain, but when pressed remarked that he should prefer to be quite free of any profession. She was not shocked, but went on sewing for a few minutes.(1989年 東大)
この動画を見る
次の英文を和訳しなさい。
John, now in his second year at college, was home for the spring vacation, and his mother took the opportunity of having a serious talk with him. Did he know where he wanted to live? John was not sure. Did he know what he wanted to do? He was equally uncertain, but when pressed remarked that he should prefer to be quite free of any profession. She was not shocked, but went on sewing for a few minutes.(1989年 東大)
否定:『同時』を表すNo soonerやHardlyやScarcely!

単元:
#英語(高校生)#英文法#否定表現・特別な表現
指導講師:
理数個別チャンネル
問題文全文(内容文):
I had no sooner arrived than it began to rain.
を倒置にしよう!
そして、別の表現で書き換えよう!
この動画を見る
I had no sooner arrived than it began to rain.
を倒置にしよう!
そして、別の表現で書き換えよう!
【数Ⅱ】図形と方程式:束の考え方…我々は一体何をさせられているのか。

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの円
$x^2+y^2=25$
$(x-4)^2+(y-3)^2=2$
について
(1)2つの円の交点を通る直線の式を求めよ
(2)2つの円の交点と(3,1)を通る円の式を求めよ
この動画を見る
2つの円
$x^2+y^2=25$
$(x-4)^2+(y-3)^2=2$
について
(1)2つの円の交点を通る直線の式を求めよ
(2)2つの円の交点と(3,1)を通る円の式を求めよ
【英語】時制など:選択問題で正答率を上げる ~解説編~

単元:
#英語(高校生)#英文法#時制
指導講師:
理数個別チャンネル
問題文全文(内容文):
By the end of next year, I ( ) for thirty years.
1.will be lived
2.will have lived
3.have lived
4.could live
この動画を見る
By the end of next year, I ( ) for thirty years.
1.will be lived
2.will have lived
3.have lived
4.could live
【数検2級】数学検定2級 問題9~問題12

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題9.整式$x^4+3x^2+3x-2$を$x^2-2x+2$で割ったときの余りを求めなさい。
問題10.xy平面上の2点A(-2,0),B(4,-3)を結んでできる線分ABを2:1に内分する点Pの座標を求めなさい。
問題11.次の計算をしなさい。
$\log_{10}\dfrac{1}{36}+2\log_{10}\dfrac{6}{5}-\log_{10}4$
問題12.$0\leqq\theta\leqq 2\pi$のとき、次の方程式を満たす$\theta$の値を求めなさい。
$-2\sin\theta+1=0$
この動画を見る
問題9.整式$x^4+3x^2+3x-2$を$x^2-2x+2$で割ったときの余りを求めなさい。
問題10.xy平面上の2点A(-2,0),B(4,-3)を結んでできる線分ABを2:1に内分する点Pの座標を求めなさい。
問題11.次の計算をしなさい。
$\log_{10}\dfrac{1}{36}+2\log_{10}\dfrac{6}{5}-\log_{10}4$
問題12.$0\leqq\theta\leqq 2\pi$のとき、次の方程式を満たす$\theta$の値を求めなさい。
$-2\sin\theta+1=0$
【英語】強い否定語を動物たちが紹介!【not/no/neverなどの使い方と意味の違い】

単元:
#英語(高校生)#英文法#否定表現・特別な表現
指導講師:
理数個別チャンネル
問題文全文(内容文):
notやnoやneverなど「強い否定語」の使い方や違いを動物たちが分かりやすく教えてくれます!
この動画を見る
notやnoやneverなど「強い否定語」の使い方や違いを動物たちが分かりやすく教えてくれます!
【世界史】2022年共通テスト世界史第1問徹底解説

単元:
#社会(高校生)#世界史#大学入試過去問・共通テスト・模試関連
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022共通テスト世界史について解説動画を作ってみました。大問毎に分けて作成していきます。
問1:中国の解剖学・薬学・植物学について
問2:東南アジアのオランダの拠点について
問3:中国と朝鮮の関係の歴史について
問4:イスラム教に関する資料読み取りについて
問5:イランにおけるキリスト教の歴史について
問6:アッバース朝下の出来事について
問7:金(中国)の歴史について
問8:チベット仏教の歴史について
問9:中国における記録書について
この動画を見る
2022共通テスト世界史について解説動画を作ってみました。大問毎に分けて作成していきます。
問1:中国の解剖学・薬学・植物学について
問2:東南アジアのオランダの拠点について
問3:中国と朝鮮の関係の歴史について
問4:イスラム教に関する資料読み取りについて
問5:イランにおけるキリスト教の歴史について
問6:アッバース朝下の出来事について
問7:金(中国)の歴史について
問8:チベット仏教の歴史について
問9:中国における記録書について
【数検2級】数学検定2級 問題4~問題8

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題4. 2次関数$y=x^2+4x+a$の最小値が1となるように、定数aの値を定めなさい。
問題5. $0°\leqq\theta\leqq 180°$とします。$\tan\theta=\dfrac{1}{2}$のとき、$\cos\theta$の値を求めなさい。
問題6. 3個のさいころを同時に振るとき、3個とも異なる目が出る確率を求めなさい。ただし、さいころの目は1から6まであり、どの目も出る確率は等しいものとします。
問題7. 2進法で表された数$1011010_{(2)}$を10進法で表しなさい。
問題8. 次の計算をしなさい。$\dfrac{x+1}{x+2} -\dfrac{x+2}{x+3}$
この動画を見る
問題4. 2次関数$y=x^2+4x+a$の最小値が1となるように、定数aの値を定めなさい。
問題5. $0°\leqq\theta\leqq 180°$とします。$\tan\theta=\dfrac{1}{2}$のとき、$\cos\theta$の値を求めなさい。
問題6. 3個のさいころを同時に振るとき、3個とも異なる目が出る確率を求めなさい。ただし、さいころの目は1から6まであり、どの目も出る確率は等しいものとします。
問題7. 2進法で表された数$1011010_{(2)}$を10進法で表しなさい。
問題8. 次の計算をしなさい。$\dfrac{x+1}{x+2} -\dfrac{x+2}{x+3}$
【数検2級】数学検定2級 問題1~問題3

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.次の式を展開して計算しなさい。
$(x+1)^2(x-1)^2$
問題2.次の式を因数分解しなさい。
$8a^2+22a+15$
問題3.次の式の分母を有理化しなさい。
$\dfrac{2}{\sqrt7}-1$
この動画を見る
問題1.次の式を展開して計算しなさい。
$(x+1)^2(x-1)^2$
問題2.次の式を因数分解しなさい。
$8a^2+22a+15$
問題3.次の式の分母を有理化しなさい。
$\dfrac{2}{\sqrt7}-1$
【受験算数】単位換算・速さ:時間との区別が大事!速さの単位変換

【受験算数】単位換算・速さ:苦手な人が多い時間の単位換算をマスターしよう!

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#速さ#速さその他
指導講師:
理数個別チャンネル
問題文全文(内容文):
案外できない人が多い時間の単位変換です。速さとの違いに注意!
この動画を見る
案外できない人が多い時間の単位変換です。速さとの違いに注意!
【中学数学】相似な図形:線分比と面積比の巧みな利用
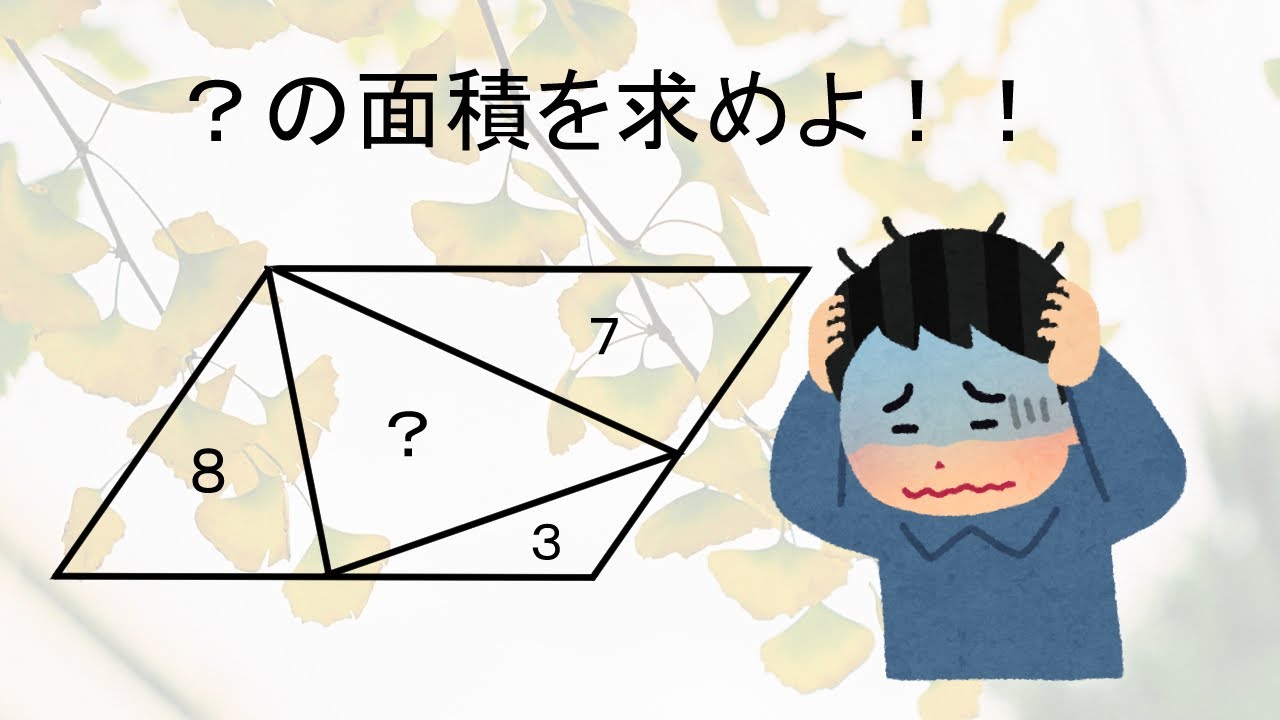
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
この動画を見る
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
【英語】英作文の基本 ~ポイント~

【英語】英作文の基本 ~例題~

【受験理科】溶液:溶けている状態とは

【受験理科】気象:エルニーニョ現象とラニーニャ現象はどう違うの??

単元:
#理科(中学受験)#地学分野#理科(中学生)#地学
指導講師:
理数個別チャンネル
問題文全文(内容文):
エルニーニョ現象とラニーニャ現象の【雲の出来る場所】と【海水温】の関係とは??
この動画を見る
エルニーニョ現象とラニーニャ現象の【雲の出来る場所】と【海水温】の関係とは??
【世界史】『ナポレオンのトリビア』

単元:
#社会(高校生)#世界史#近代ヨーロッパ・アメリカ世界の成立
指導講師:
理数個別チャンネル
問題文全文(内容文):
世界史で頻出のナポレオンの『ちょっと得する豆知識』を紹介!
「鉛筆のトリビア」
「缶詰のトリビア」
「アルプス越えのトリビア」
「ナポレオンの○○時間のトリビア」
この動画を見る
世界史で頻出のナポレオンの『ちょっと得する豆知識』を紹介!
「鉛筆のトリビア」
「缶詰のトリビア」
「アルプス越えのトリビア」
「ナポレオンの○○時間のトリビア」
【英検ライティング】ボディ(理由)が思いつかない人必見!魔法の思考術と実践【英検2級・準1級向け】

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
It is sometimes said that all people should be able to enter museums for free. Do you agree with this opinion?
●Donations
●Learning environment
●Maintenance
この動画を見る
It is sometimes said that all people should be able to enter museums for free. Do you agree with this opinion?
●Donations
●Learning environment
●Maintenance
【英語】比較:『クジラ構文』を解説!

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#構文#比較
指導講師:
理数個別チャンネル
問題文全文(内容文):
「『クジラ構文』って聞いたことあるけど、なんだかわからない~」という人向けの解説動画です!
この動画を見る
「『クジラ構文』って聞いたことあるけど、なんだかわからない~」という人向けの解説動画です!
【英検ライティング】ボディ(理由)が思いつかない人必見!魔法の思考術と実践 ~英検2級・準1級向け~

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
It is sometimes said that all people should be able to enter museums for free. Do you agree with this opinion?
●Donations
●Learning environment
●Maintenance
この動画を見る
It is sometimes said that all people should be able to enter museums for free. Do you agree with this opinion?
●Donations
●Learning environment
●Maintenance
「接続詞」のwhere(2011年早稲田大)

単元:
#英語(高校生)#英文法#接続詞#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#早稲田大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
接続詞のwhereについて説明します。
次の英文を和訳しなさい。
He hypothesized that air was something interfering in the fall of the feather and that if an experiment could be done where there is no air, then the hammer and feather would fall at the same speed.
(2011早稲田理系)
この動画を見る
接続詞のwhereについて説明します。
次の英文を和訳しなさい。
He hypothesized that air was something interfering in the fall of the feather and that if an experiment could be done where there is no air, then the hammer and feather would fall at the same speed.
(2011早稲田理系)
【英検2級】リーディングの長文問題の解き方見せます

単元:
#英語(高校生)#長文読解#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
リーディングの長文問題の解き方見せます
この動画を見る
リーディングの長文問題の解き方見せます
【英検2級】最新テンプレで「反対(disagree)」で書くやり方を紹介します

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
Some people say that more apartment buildings should allow pets such as dogs and cats. Do you agree with this opinion?
●Cleanliness
●Lifestyles
●Neighbors
この動画を見る
Some people say that more apartment buildings should allow pets such as dogs and cats. Do you agree with this opinion?
●Cleanliness
●Lifestyles
●Neighbors
【英検3級】How oftenで始まる疑問文で聞かれた場合の満点ライティングを紹介

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
How often do you travel?
この動画を見る
How often do you travel?
【速報】共通テスト英語リーディング(2022)第4問の解説 ~引っかけ多数~

単元:
#英語(高校生)#大学入試過去問(英語)#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テスト(英語)2022年度の第4問を同日に解いてみた感想と、実際の解き方を一挙公開!!です。
この動画を見る
共通テスト(英語)2022年度の第4問を同日に解いてみた感想と、実際の解き方を一挙公開!!です。
【受験理科】人体③『呼吸・循環(2つの呼吸)』

単元:
#理科(中学受験)#生物分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
人体の消化吸収をわかりやすく説明します!
人体の「2つの呼吸」について
「外呼吸」について
「内呼吸」について
この動画を見る
人体の消化吸収をわかりやすく説明します!
人体の「2つの呼吸」について
「外呼吸」について
「内呼吸」について
【日本最速解答速報】共通テスト英語リーディング(2022)第4問の解説 ~引っかけ多数~

単元:
#英語(高校生)#大学入試過去問(英語)#大学入試解答速報#英語#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テスト英語リーディング(2022)第4問の解説をしていきます.
この動画を見る
共通テスト英語リーディング(2022)第4問の解説をしていきます.
【受験理科】人体②『吸収・排出(う〇ちとお〇っこ)』





