 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】『授業動画【仕事算】』

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
理数個別チャンネル
問題文全文(内容文):
1.スコップ1回で5kgの砂を運べる。500kgの砂を運びたい時、スコップ何回で運べるか?
2.水槽にAの水道管だけで水を入れると60時間、Bの水道管だけだと40時間、Cの水道管だけなら24時間、満水にするために時間がかかります。AとBとCの水道管で同時に水を入れたところ、途中でAの水道管が故障していたため満水にするために13時間かかりました。Aの水道管が動いていた時間は何時間ですか?
この動画を見る
1.スコップ1回で5kgの砂を運べる。500kgの砂を運びたい時、スコップ何回で運べるか?
2.水槽にAの水道管だけで水を入れると60時間、Bの水道管だけだと40時間、Cの水道管だけなら24時間、満水にするために時間がかかります。AとBとCの水道管で同時に水を入れたところ、途中でAの水道管が故障していたため満水にするために13時間かかりました。Aの水道管が動いていた時間は何時間ですか?
【受験算数】『授業動画【電車の通過算】』
単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
理数個別チャンネル
問題文全文(内容文):
電車が秒速2mで歩く人を10秒で追い越し、秒速15mで走るバイクを36秒で追い越します。
(1)電車の速さは秒速何mですか?
(2)電車の長さは何mですか?
この動画を見る
電車が秒速2mで歩く人を10秒で追い越し、秒速15mで走るバイクを36秒で追い越します。
(1)電車の速さは秒速何mですか?
(2)電車の長さは何mですか?
【受験理科】『授業動画【電熱線と発熱量】』

単元:
#理科(中学受験)#物理分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
電熱線の発熱量を、並列回路・直列回路・並列回路∔直列回路で大小関係を比較して考える動画です。
この動画を見る
電熱線の発熱量を、並列回路・直列回路・並列回路∔直列回路で大小関係を比較して考える動画です。
【受験算数】『授業動画【バイクの旅人算】』

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算#ダイヤグラム
指導講師:
理数個別チャンネル
問題文全文(内容文):
「父が兄弟を交互にバイクに乗せて目的地に連れていく旅人算の問題」を①算で解いてみました。
父、兄、 弟が同時に22km離れた目的地に向かう。
父は時速36kmのバイクでまず弟を目的地の手前まで運び、 弟はそこから時速4kmで目的地に向かった。父はすぐに引き返して時速6kmで歩いてきた兄と合流したら兄を乗せて目的地に向かったところ、歩いていた弟と同時に目的地に到着した。
弟は目的地の何km手前から歩き始めたか?
この動画を見る
「父が兄弟を交互にバイクに乗せて目的地に連れていく旅人算の問題」を①算で解いてみました。
父、兄、 弟が同時に22km離れた目的地に向かう。
父は時速36kmのバイクでまず弟を目的地の手前まで運び、 弟はそこから時速4kmで目的地に向かった。父はすぐに引き返して時速6kmで歩いてきた兄と合流したら兄を乗せて目的地に向かったところ、歩いていた弟と同時に目的地に到着した。
弟は目的地の何km手前から歩き始めたか?
【数Ⅱ】二項定理を覚えられない人へ

【受験理科】『授業動画【光の色と波長】』

【受験理科】化学:気体の発生②

【中学受験理科】【模試解説集】化学:気体の発生②

単元:
#理科(中学受験)#化学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
鉄と亜鉛に塩酸Aを加えて気体Pを発生させ、(図)のような方法で集める実験を行いました。これについて、次の問いに答えなさい。
<実験1>
①~④の番号をつけた三角フラスコに、いろいろな重さの亜鉛の粉末を入れ、塩酸Aを150㎤ずつ加え、発生する気体Pの体積を調べた。
<実験2>
⑤~⑧の番号をつけた三角フラスコに、いろいろな重さの鉄の粉末を入れ、塩酸を150㎤ずつ加え、発生する気体Pの体積を調べた。
問5 三角フラスコに鉄5.6gを入れて、実験で使った塩酸A250㎡を反応させると鉄はすべて溶けました。残った塩酸Aに亜鉛を加えるとき、残った塩酸Aと過不足なく反応する亜鉛の重さは何gですか。数字で答えなさい。
問6 鉄と亜鉛の粉末をあわせて15g用意し、塩酸Aを十分に加えてすべて溶かしたところ、気体Pが6L発生しました。この粉末にふくまれる鉄は何gですか。数字で答えなさい。
この動画を見る
鉄と亜鉛に塩酸Aを加えて気体Pを発生させ、(図)のような方法で集める実験を行いました。これについて、次の問いに答えなさい。
<実験1>
①~④の番号をつけた三角フラスコに、いろいろな重さの亜鉛の粉末を入れ、塩酸Aを150㎤ずつ加え、発生する気体Pの体積を調べた。
<実験2>
⑤~⑧の番号をつけた三角フラスコに、いろいろな重さの鉄の粉末を入れ、塩酸を150㎤ずつ加え、発生する気体Pの体積を調べた。
問5 三角フラスコに鉄5.6gを入れて、実験で使った塩酸A250㎡を反応させると鉄はすべて溶けました。残った塩酸Aに亜鉛を加えるとき、残った塩酸Aと過不足なく反応する亜鉛の重さは何gですか。数字で答えなさい。
問6 鉄と亜鉛の粉末をあわせて15g用意し、塩酸Aを十分に加えてすべて溶かしたところ、気体Pが6L発生しました。この粉末にふくまれる鉄は何gですか。数字で答えなさい。
【受験理科】化学:気体の発生①
【中学受験理科】【模試解説集】化学:気体の発生①
単元:
#理科(中学受験)#化学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
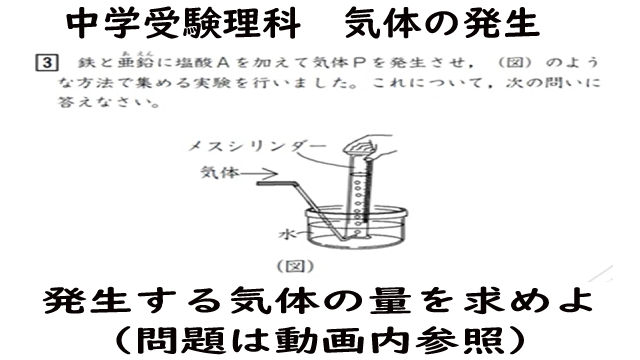
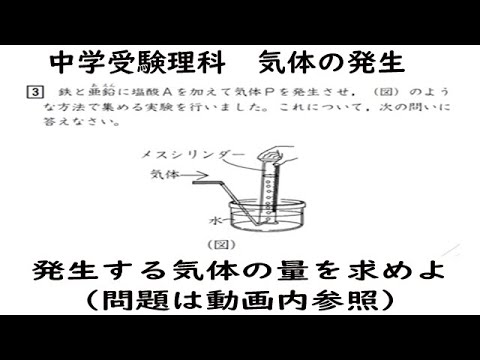
鉄と亜鉛に塩酸Aを加えて気体Pを発生させ、(図)のような方法で集める実験を行いました。これについて、次の問いに答えなさい。
<実験1>
①~④の番号をつけた三角フラスコに、いろいろな重さの亜鉛の粉末を入れ、塩酸Aを150㎤ずつ加え、発生する気体Pの体積を調べた。
<実験2>
⑤~⑧の番号をつけた三角フラスコに、いろいろな重さの鉄の粉末を入れ、塩酸を150㎤ずつ加え、発生する気体Pの体積を調べた。
問3 実験で使った塩酸を2倍にうすめて、塩酸Bをつくりました。このあと三角フラスコに亜鉛を5.5g入れ、塩酸Bを100㎡加えて反応させました。これについて、下の問いに答えなさい。
(1) この反応が終わったあとに、亜鉛か塩酸Bのいずれかが残りました。残った物質を下から選び、記号で答えなさい。また、残った量を数字で答え、正しい単位を○で囲みなさい。
(ア) 亜鉛 (イ) 塩酸
(2) この反応で発生した気体Pは何Lですか。数字で答えなさい。
問4 塩酸A100c㎡と過不足なく反応する鉄の重さは何gですか。数字で答えなさい。
この動画を見る
鉄と亜鉛に塩酸Aを加えて気体Pを発生させ、(図)のような方法で集める実験を行いました。これについて、次の問いに答えなさい。
<実験1>
①~④の番号をつけた三角フラスコに、いろいろな重さの亜鉛の粉末を入れ、塩酸Aを150㎤ずつ加え、発生する気体Pの体積を調べた。
<実験2>
⑤~⑧の番号をつけた三角フラスコに、いろいろな重さの鉄の粉末を入れ、塩酸を150㎤ずつ加え、発生する気体Pの体積を調べた。
問3 実験で使った塩酸を2倍にうすめて、塩酸Bをつくりました。このあと三角フラスコに亜鉛を5.5g入れ、塩酸Bを100㎡加えて反応させました。これについて、下の問いに答えなさい。
(1) この反応が終わったあとに、亜鉛か塩酸Bのいずれかが残りました。残った物質を下から選び、記号で答えなさい。また、残った量を数字で答え、正しい単位を○で囲みなさい。
(ア) 亜鉛 (イ) 塩酸
(2) この反応で発生した気体Pは何Lですか。数字で答えなさい。
問4 塩酸A100c㎡と過不足なく反応する鉄の重さは何gですか。数字で答えなさい。
【英語】ヤバい和製英語紹介!ドラクエにも出てきた!?

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#名詞・冠詞・代名詞#形容詞・副詞#会話文#勉強法・その他#その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
和製英語には別の意味で伝わってしまうものがたくさんあります!ここで確認しておこう!ドラクエにも和製英語出てきたよ!
この動画を見る
和製英語には別の意味で伝わってしまうものがたくさんあります!ここで確認しておこう!ドラクエにも和製英語出てきたよ!
【数Ⅰ】図形と計量:三角比:【超重要】斜辺と角から線分の長さを求める!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【超重要】直角三角形の「斜辺」と「角」を用いて他の辺を表せ!
この動画を見る
【超重要】直角三角形の「斜辺」と「角」を用いて他の辺を表せ!
【数Ⅱ】間違えやすい? 点と直線の距離の公式の覚え方

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
この動画を見る
点と直線の距離の公式がどっちだっけ…となったとき、そんなときのための講義です。
【受験理科】『授業動画【光の屈折プロレス編】』

【英語】前置詞asの後に形容詞?前置詞の後ろって名詞じゃないの?!

単元:
#英語(高校生)#英文法#前置詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
前置詞のasの後ろに形容詞しか書かれていない・・・。そんな基本ルールを逸脱するasの考え方です。
この動画を見る
前置詞のasの後ろに形容詞しか書かれていない・・・。そんな基本ルールを逸脱するasの考え方です。
Lesson11-2 ニュートレジャー Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#There is~の文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson11-2 ニュートレジャー Stage1 3rd Edition解説していきます.
この動画を見る
Lesson11-2 ニュートレジャー Stage1 3rd Edition解説していきます.
Lesson11-2 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中2英語#文型(第1文型、第2文型、第3文型、第4文型、第5文型)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson11#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson11-2 N.T. ENGLISH SERIES Third Edition Stage1
there is 構文
この動画を見る
Lesson11-2 N.T. ENGLISH SERIES Third Edition Stage1
there is 構文
Lesson11-1 ニュートレジャー Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#There is~の文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson11-1 ニュートレジャー Stage1 3rd Edition解説していきます.
この動画を見る
Lesson11-1 ニュートレジャー Stage1 3rd Edition解説していきます.
Lesson11-1 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#There is~の文(肯定文・否定文・疑問文)#可算名詞・不可算名詞、冠詞a,an,the
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson11#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson11-1 N.T. ENGLISH SERIES Third Edition Stage1
there is 構文
この動画を見る
Lesson11-1 N.T. ENGLISH SERIES Third Edition Stage1
there is 構文
図形と計量空間の基本1 【烈's study!がていねいに解説】
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
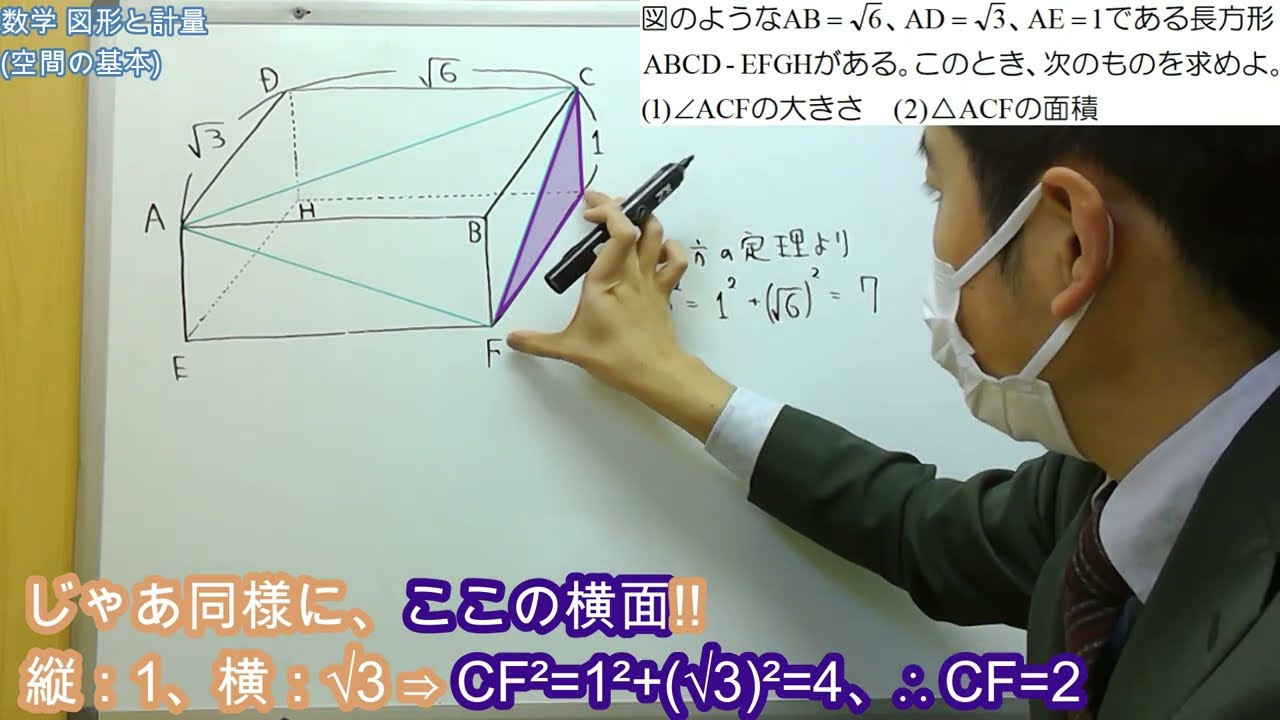
右の図のような$AB=\sqrt6、AD=\sqrt3、AE=1$である直方体$ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\angle ACF$の大きさ
(2)$△ACF$の面積
この動画を見る
右の図のような$AB=\sqrt6、AD=\sqrt3、AE=1$である直方体$ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\angle ACF$の大きさ
(2)$△ACF$の面積
Lesson9-3 ニュートレジャー Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#時刻の表し方とたずね方、曜日・日付のたずね方、When~?、「時」を表す前置詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Third Edition Stage1 Lesson9-3の解説です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Third Edition Stage1 Lesson9-3の解説です。
Lesson9-3 NT Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#時刻の表し方とたずね方、曜日・日付のたずね方、When~?、「時」を表す前置詞
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson9#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-3の解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-3の解説です。
Lesson9-2 ニュートレジャー Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-2の解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-2の解説です。
Lesson9-2 NT Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#過去進行形(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson9#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-2の解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson9-2の解説です。
Lesson7-3 ニュートレジャー Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson7-3のKeyPoint例文解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson7-3のKeyPoint例文解説です。
Lesson7-3 NT Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson7#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson7-3のKeyPoint例文解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson7-3のKeyPoint例文解説です。
Lesson7-2 ニュートレジャー Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson7-2のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson7-2のKeyPoint例文解説です。
Lesson7-2 NT Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#現在進行形(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson7#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson7-2のKeyPoint例文解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson7-2のKeyPoint例文解説です。
図形と計量 余弦定理応用2【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
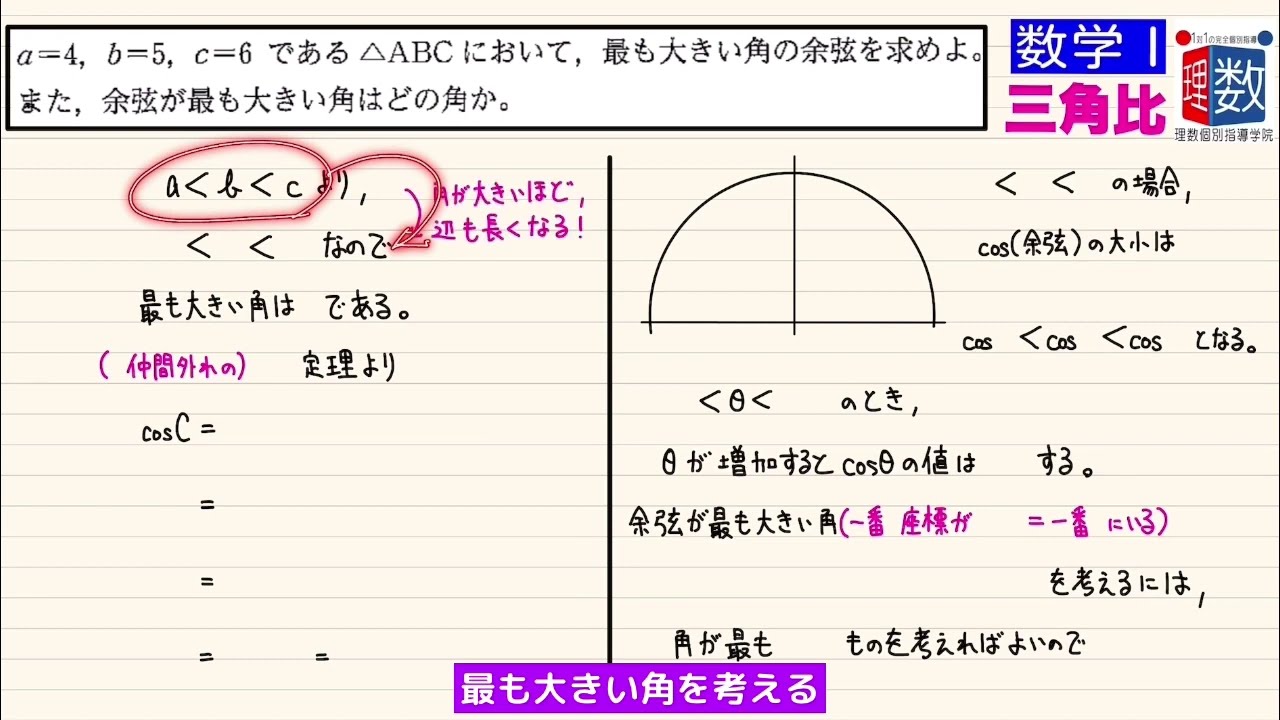
$a=4,b=5,c=6$ である$△ABC$において,最も大きい角の余弦を求めよ。また,余弦が最も大きい角はどの角か。
この動画を見る
$a=4,b=5,c=6$ である$△ABC$において,最も大きい角の余弦を求めよ。また,余弦が最も大きい角はどの角か。
図形と計量 余弦定理応用1【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各場合について,$△ABC$ の残りの辺の長さと角の大きさを求めよ。
(1) $b=3,c=\sqrt3,B=60°$
(2) $b=2\sqrt3,c=2,C=30°$
この動画を見る
次の各場合について,$△ABC$ の残りの辺の長さと角の大きさを求めよ。
(1) $b=3,c=\sqrt3,B=60°$
(2) $b=2\sqrt3,c=2,C=30°$




