 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【英語】Lesson1-1 ① Stage1 【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#be動詞の過去形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
私立中1英語の教科書の文法解説と例文解説、be動詞の現在形の肯定文です。
この動画を見る
私立中1英語の教科書の文法解説と例文解説、be動詞の現在形の肯定文です。
Lesson1-1 ① NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson1#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
私立中1英語の教科書の文法解説と例文解説、be動詞の現在形の肯定文です。
この動画を見る
私立中1英語の教科書の文法解説と例文解説、be動詞の現在形の肯定文です。
【中学数学】数学用語チェック絵本 vol 4 比例と反比例

【数B】ベクトル:単位ベクトルを成分で表そう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題616
$\vec{a}=(-3,4)$と同じ向きの単位ベクトル$\vec{e}$を求めよ。
この動画を見る
アドバンスプラス数学B
問題616
$\vec{a}=(-3,4)$と同じ向きの単位ベクトル$\vec{e}$を求めよ。
【数C】単位ベクトルを成分で表そう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題616
vec(a)=(-3,4)と同じ向きの単位ベクトルvec(e)を求めよ。
この動画を見る
アドバンスプラス数学B
問題616
vec(a)=(-3,4)と同じ向きの単位ベクトルvec(e)を求めよ。
【中学数学】数学用語チェック絵本 vol 3 方程式

【まだまだ使えます】【英検2級】2022年度2回のライティング問題に「英検2級のテンプレ動画」を当てはめてみた。【日本最速解答速報】

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
Some people say that Japan should accept more people from other countries to work in Japan.
Do you agree with this opinion?
POINTS
Aging society
Culture
Language
この動画を見る
Some people say that Japan should accept more people from other countries to work in Japan.
Do you agree with this opinion?
POINTS
Aging society
Culture
Language
【受験算数】流水算・通過算:(練習❹)通過算と和差算【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)長さ280mの列車Aと、長さ200mの列車Bがあります。列車Aと列車Bが出会ってからはなれるまでに10秒、列車Aが列車Bに追いついてから追いこすまでに30秒かかりました。列車Aの速さは時速何kmですか。
(2)時速72kmで進んでいる列車がトンネルに入り始めて20秒後には、列車の先頭がトンネルの全長の2/5のところまで進みました。その後、この電車がトンネルを出終わるまでに36秒かかりました。トンネルの長さと列車の長さはそれぞれ何mですか。
この動画を見る
(1)長さ280mの列車Aと、長さ200mの列車Bがあります。列車Aと列車Bが出会ってからはなれるまでに10秒、列車Aが列車Bに追いついてから追いこすまでに30秒かかりました。列車Aの速さは時速何kmですか。
(2)時速72kmで進んでいる列車がトンネルに入り始めて20秒後には、列車の先頭がトンネルの全長の2/5のところまで進みました。その後、この電車がトンネルを出終わるまでに36秒かかりました。トンネルの長さと列車の長さはそれぞれ何mですか。
【中学受験理科】物理:焦点距離6cmのレンズの中心から10cmの位置に物体を置いた時の像の大きさを求めよ
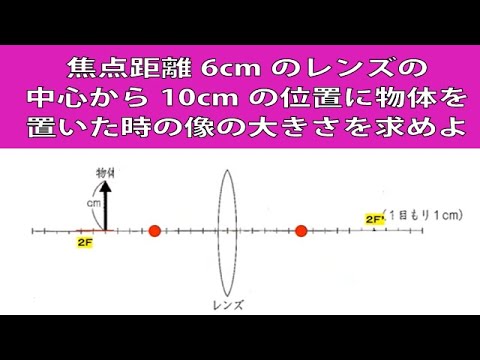
【受験理科】物理:焦点距離6cmのレンズの中心から10cmの位置に物体を置いた時の像の大きさを求めよ

【数C】ベクトルが「平行」であるときの典型解法をおさえよう!

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題615
vec(a)=(1,x),vec(b)=(x,4)が平行であるような実数xの値を求めよ。
この動画を見る
アドバンスプラス数学B
問題615
vec(a)=(1,x),vec(b)=(x,4)が平行であるような実数xの値を求めよ。
【数B】ベクトル:ベクトルが「平行」であるときの典型解法をおさえよう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題615
$\vec{a}=(1,x),\vec{b}=(x,4)$が平行であるような実数xの値を求めよ。
この動画を見る
アドバンスプラス数学B
問題615
$\vec{a}=(1,x),\vec{b}=(x,4)$が平行であるような実数xの値を求めよ。
【受験算数】流水算・通過算:(練習❸)流水算:エンジンが止まるとき【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
船が川の下流のA地点から45km上流のB地点まで行くのに、いつもは5時間かかります。ある日、エンジンが途中で20分間動かなくなったので、A地点からB地点まで行くのに5時間28分かかりました。船の静水での速さと川の流れの速さはそれぞれ一定として、次の問いに答えなさい。
(1)この川の流れの速さは毎時何kmですか。
(2)いつもはA地点とB地点を往復するのに何時間かかりますか。
この動画を見る
船が川の下流のA地点から45km上流のB地点まで行くのに、いつもは5時間かかります。ある日、エンジンが途中で20分間動かなくなったので、A地点からB地点まで行くのに5時間28分かかりました。船の静水での速さと川の流れの速さはそれぞれ一定として、次の問いに答えなさい。
(1)この川の流れの速さは毎時何kmですか。
(2)いつもはA地点とB地点を往復するのに何時間かかりますか。
【数B】ベクトル:ベクトルの基本⑬内心ベクトルの求め方

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
角$A=60°,AB=8,AC=5$である三角形ABCの内心をIとする。$AB=b,AC=c$とするときAIをb,cを用いて表せ.
この動画を見る
角$A=60°,AB=8,AC=5$である三角形ABCの内心をIとする。$AB=b,AC=c$とするときAIをb,cを用いて表せ.
【数C】ベクトルの基本⑬内心ベクトルの求め方

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
角A=60°,AB=8,AC=5である三角形ABCの内心をIとする。AB=b,AC=cとするときAIをb,cを用いて表せ
この動画を見る
角A=60°,AB=8,AC=5である三角形ABCの内心をIとする。AB=b,AC=cとするときAIをb,cを用いて表せ
【受験理科】物理:レンズ①作図の基本をわかりやすく解説します
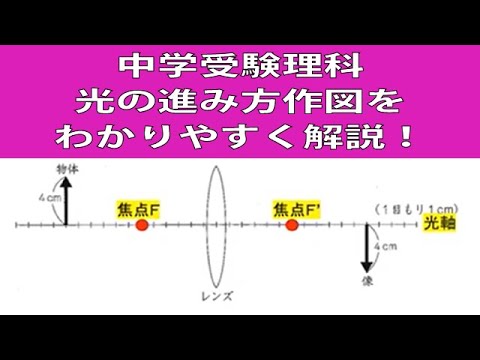
【中学受験理科】物理:レンズ①作図の基本をわかりやすく解説します

【受験算数】流水算・通過算:(練習❷)流速が変わる流水算【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある船は、川下のA地点から60km上流にあるB地点まで上るのに、いつもなら5時間かかります。ある日、川の流れの速さがいつもの2倍になっていたので、A地点からB地点まで上るのに6時間かかりました。これについて、次の問いに答えなさい。
(1)この船の静水時の速さは毎時何kmですか。
(2)この日、B地点からA地点まで下るのに何時間何分かかりますか。
この動画を見る
ある船は、川下のA地点から60km上流にあるB地点まで上るのに、いつもなら5時間かかります。ある日、川の流れの速さがいつもの2倍になっていたので、A地点からB地点まで上るのに6時間かかりました。これについて、次の問いに答えなさい。
(1)この船の静水時の速さは毎時何kmですか。
(2)この日、B地点からA地点まで下るのに何時間何分かかりますか。
【数B】ベクトル:ベクトルの基本⑫位置ベクトルの考え方

【数C】ベクトルの基本⑫位置ベクトルの考え方

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
位置ベクトルの考え方についての動画です!
この動画を見る
位置ベクトルの考え方についての動画です!
【受験算数】流水算・通過算:(練習❶)流速がわからない流水算【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
川の上流にある北町から下流にある南町までの60kmを往復する2せきの船A、Bがあります。いま、A、Bがそれぞれ北町と南町を同時に出発したところ、北町から下流に36kmの地点で初めて出会いました。A、Bの静水時の速さはそれぞれ毎時16km、毎時14kmとするとき、この川の流れの速さは毎時何kmですか。
この動画を見る
川の上流にある北町から下流にある南町までの60kmを往復する2せきの船A、Bがあります。いま、A、Bがそれぞれ北町と南町を同時に出発したところ、北町から下流に36kmの地点で初めて出会いました。A、Bの静水時の速さはそれぞれ毎時16km、毎時14kmとするとき、この川の流れの速さは毎時何kmですか。
【英語】50音順に文法用語を解説する③可算名詞編

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中2英語#名詞・冠詞・代名詞#可算名詞・不可算名詞、冠詞a,an,the
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は可算名詞の基本について解説しています。
この動画を見る
今回は可算名詞の基本について解説しています。
【英語】50音順に文法用語を解説するシリーズ②「過去分詞」編

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#受動態#分詞・分詞構文#受動態#現在完了(継続、経験、完了・結果)#分詞(現在分詞の形容詞的用法、過去分詞の形容詞的用法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第二回は『過去分詞』です。前半は過去分詞の用法を、後半は過去分詞の大切なポイントを解説しています。
この動画を見る
第二回は『過去分詞』です。前半は過去分詞の用法を、後半は過去分詞の大切なポイントを解説しています。
【数C】ベクトルの基本⑪平面ベクトルのときの三角形の面積の計算

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点A(-2,1),B(3,0),C(2,4)が与えられたとき、三角形ABCの面積を求めよ
この動画を見る
3点A(-2,1),B(3,0),C(2,4)が与えられたとき、三角形ABCの面積を求めよ
【数B】ベクトル:ベクトルの基本⑪平面ベクトルのときの三角形の面積の計算

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点$A(-2,1),B(3,0),C(2,4)$が与えられたとき、三角形ABCの面積を求めよ
この動画を見る
3点$A(-2,1),B(3,0),C(2,4)$が与えられたとき、三角形ABCの面積を求めよ
【受験算数】過不足算を使ってとうもろこしの数を求めよう!

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
教材:
#SPX#6年算数D-SPX#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
とうもろこしをいくつかの箱に入れてみたところ、次のことが分かりました。
(A)とうもろこしをある本数ずつ入れると、箱が5つ余りました。
また、とうもろこしが3本入った箱が1箱だけ出来ました。
(B)1箱あたりのとうもろこしの本数を(A)よりも5本少なくすると、とうもろこしが56本余りました。
(C)1箱あたりのとうもろこしの本数を(A)よりも3本少なくすると、とうもろこしが6本余りました。
このとき次の問いに答えなさい。
(1)箱はいくつありますか。
(2)とうもろこしは何本ありますか。
この動画を見る
とうもろこしをいくつかの箱に入れてみたところ、次のことが分かりました。
(A)とうもろこしをある本数ずつ入れると、箱が5つ余りました。
また、とうもろこしが3本入った箱が1箱だけ出来ました。
(B)1箱あたりのとうもろこしの本数を(A)よりも5本少なくすると、とうもろこしが56本余りました。
(C)1箱あたりのとうもろこしの本数を(A)よりも3本少なくすると、とうもろこしが6本余りました。
このとき次の問いに答えなさい。
(1)箱はいくつありますか。
(2)とうもろこしは何本ありますか。
【受験算数】過不足算:過不足算を使ってとうもろこしの数を求めよう!

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
理数個別チャンネル
問題文全文(内容文):
とうもろこしをいくつかの箱に入れてみたところ、次のことが分かりました。
(A)とうもろこしをある本数ずつ入れると、箱が5つ余りました。
また、とうもろこしが3本入った箱が1箱だけ出来ました。
(B)1箱あたりのとうもろこしの本数を(A)よりも5本少なくすると、とうもろこしが56本余りました。
(C)1箱あたりのとうもろこしの本数を(A)よりも3本少なくすると、とうもろこしが6本余りました。
このとき次の問いに答えなさい。
(1)箱はいくつありますか。
(2)とうもろこしは何本ありますか。
この動画を見る
とうもろこしをいくつかの箱に入れてみたところ、次のことが分かりました。
(A)とうもろこしをある本数ずつ入れると、箱が5つ余りました。
また、とうもろこしが3本入った箱が1箱だけ出来ました。
(B)1箱あたりのとうもろこしの本数を(A)よりも5本少なくすると、とうもろこしが56本余りました。
(C)1箱あたりのとうもろこしの本数を(A)よりも3本少なくすると、とうもろこしが6本余りました。
このとき次の問いに答えなさい。
(1)箱はいくつありますか。
(2)とうもろこしは何本ありますか。
【数学】二次方程式の活用:みんなが嫌いな動く点Pを得意に!

単元:
#数学(中学生)#中3数学#2次方程式
教材:
#KEYワーク#KEYワーク(数学)中2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
みんなの苦手な動点Pの問題を克服しよう!
この動画を見る
みんなの苦手な動点Pの問題を克服しよう!
【数学】2次方程式:二次方程式の活用 みんなが嫌いな動く点Pを得意に!

【英語】50音順に文法用語を解説するシリーズ①「意味上の主語」編

単元:
#英語(高校生)#英文法#英文解釈#不定詞#動名詞#分詞・分詞構文#勉強法・その他#その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は『意味上の主語』について解説します。
この動画を見る
今回は『意味上の主語』について解説します。




