 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【ここからでも楽しめる!】三角比の計算(4):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
この動画を見る
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
【中学からの!】三角比の計算(3):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
この動画を見る
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
30秒で高校入試の必須内容を身に付ける動画~全国入試問題解法 #Shorts #入試問題 #数学
単元:
#数学(中学生)#中2数学#1次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3点$A(-4,13),B(1,3),C(5,a)$は同一直線上にある.
定数$a$の値を求めよ.
この動画を見る
3点$A(-4,13),B(1,3),C(5,a)$は同一直線上にある.
定数$a$の値を求めよ.
【3分で理解する!道を外れると…!】二次方程式:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$(2x-3)^2+4(2x-3)-45=0$を解きなさい.
中央大附属高校過去問
この動画を見る
2次方程式$(2x-3)^2+4(2x-3)-45=0$を解きなさい.
中央大附属高校過去問
【安全な解法も大切なわけですが…】二次方程式:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x$の2次方程式$x^2-4ax+a^2=0$の1つの解が$x=2$のとき,
$a$の値は$\Box$である.
福岡大学附属大濠高等学校過去問
この動画を見る
$x$の2次方程式$x^2-4ax+a^2=0$の1つの解が$x=2$のとき,
$a$の値は$\Box$である.
福岡大学附属大濠高等学校過去問
【上手いやり方などと自慢するなかれ…!】平方根:愛知県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(\sqrt5+\sqrt2)^2-(\sqrt5-\sqrt2)^2$を計算しなさい.
愛知県公立高等学校過去問
この動画を見る
$(\sqrt5+\sqrt2)^2-(\sqrt5-\sqrt2)^2$を計算しなさい.
愛知県公立高等学校過去問
入試で必須の計算を15秒で習得する動画~全国入試問題解法 #Shorts #入試問題
単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(\sqrt2-\sqrt6)^2+\dfrac{12}{\sqrt3}$を計算せよ.
この動画を見る
$(\sqrt2-\sqrt6)^2+\dfrac{12}{\sqrt3}$を計算せよ.
30秒で高校入試の必出問題を身に付ける動画~全国入試問題解法 #Shorts #高校入試
単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{67-2n}$の値が整数であるとき,最も小さい$n$を求めよ.($n$は自然数)
この動画を見る
$\sqrt{67-2n}$の値が整数であるとき,最も小さい$n$を求めよ.($n$は自然数)
【基礎を軽んずれば基礎に泣く!】文字式:滋賀県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$A=4x-1$であり,$B=-2x+3$とするとき,次の式を計算しなさい.
$-4A+3B+2A$
滋賀県高校過去問
この動画を見る
$A=4x-1$であり,$B=-2x+3$とするとき,次の式を計算しなさい.
$-4A+3B+2A$
滋賀県高校過去問
【3分でケアレスミスをなくす!】文字式:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\left(-\dfrac{2}{3}a^2b\right)^2\div a^2b^3\times(-9ab^2)$を計算し,簡単にすると$\Box$である.
福岡大学附属大濠高等学校過去問
この動画を見る
$\left(-\dfrac{2}{3}a^2b\right)^2\div a^2b^3\times(-9ab^2)$を計算し,簡単にすると$\Box$である.
福岡大学附属大濠高等学校過去問
【信じて突き進もう!】連立方程式:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
正の数$x,y,z$が,$x=y(z+2)=(x+y)z$を満たしているとき
$z$の値を求めよ.また,$\dfrac{y}{x}$の値を求めよ.
ラサール高校過去問
この動画を見る
正の数$x,y,z$が,$x=y(z+2)=(x+y)z$を満たしているとき
$z$の値を求めよ.また,$\dfrac{y}{x}$の値を求めよ.
ラサール高校過去問
15秒で数学の基礎が身に付くための一軍女子~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$y=2x^2$の$x$の変域$-2\leqq x\leqq a$のとき,$y$の変域は$b\leqq y\leqq 18$である.
$a,b$の値を求めよ.
この動画を見る
$y=2x^2$の$x$の変域$-2\leqq x\leqq a$のとき,$y$の変域は$b\leqq y\leqq 18$である.
$a,b$の値を求めよ.
【中学からの!】三角比の計算(2):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
【正しい攻め方をしないと…】因数分解:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$xy^2-xz^2+2xz-x$を因数分解しなさい.
立命館高校過去問
この動画を見る
$xy^2-xz^2+2xz-x$を因数分解しなさい.
立命館高校過去問
【中学からの!】三角比の計算(1):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
数学の基礎から学ぶ15秒の七夕ダ~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中1数学#中3数学#空間図形#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
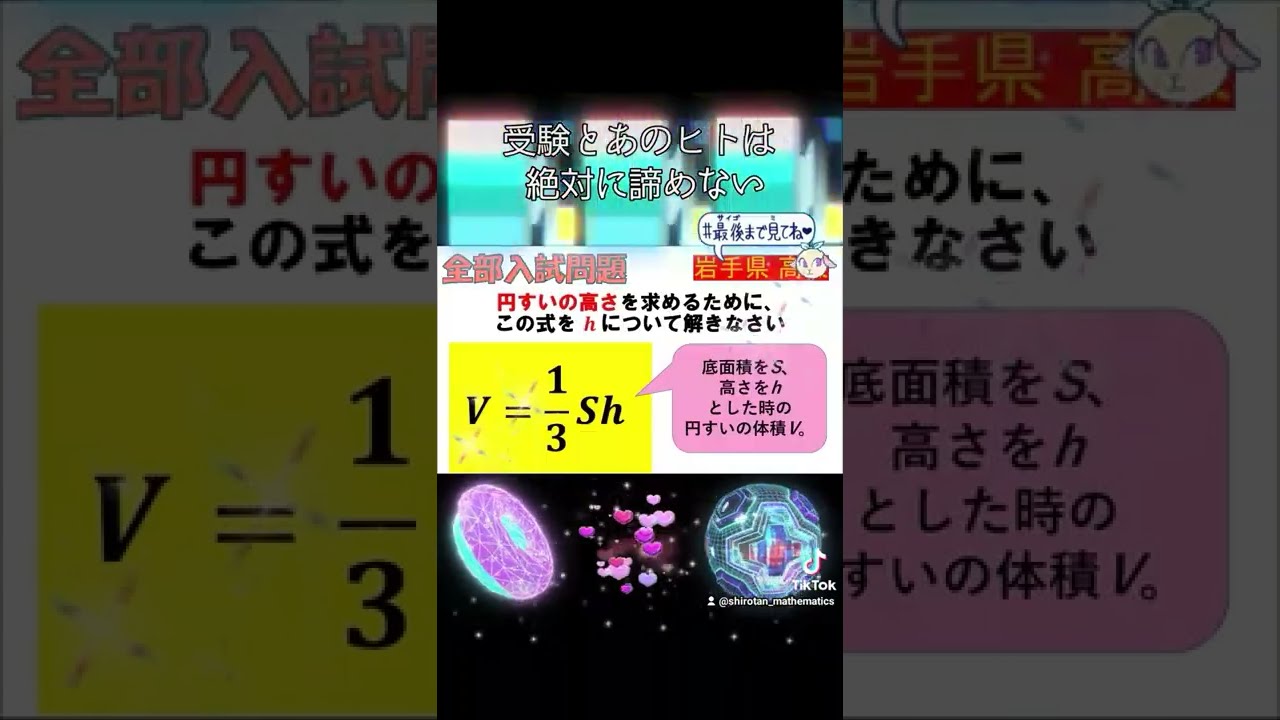
円錐の体積$V$は$V=\dfrac{1}{3}SH$である.
$H$のついて解きなさい.($S$は底面積であり,$H$は高さ)
この動画を見る
円錐の体積$V$は$V=\dfrac{1}{3}SH$である.
$H$のついて解きなさい.($S$は底面積であり,$H$は高さ)
【3分で図形の基礎から応用まで!】二次方程式:島根県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#角度と面積#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
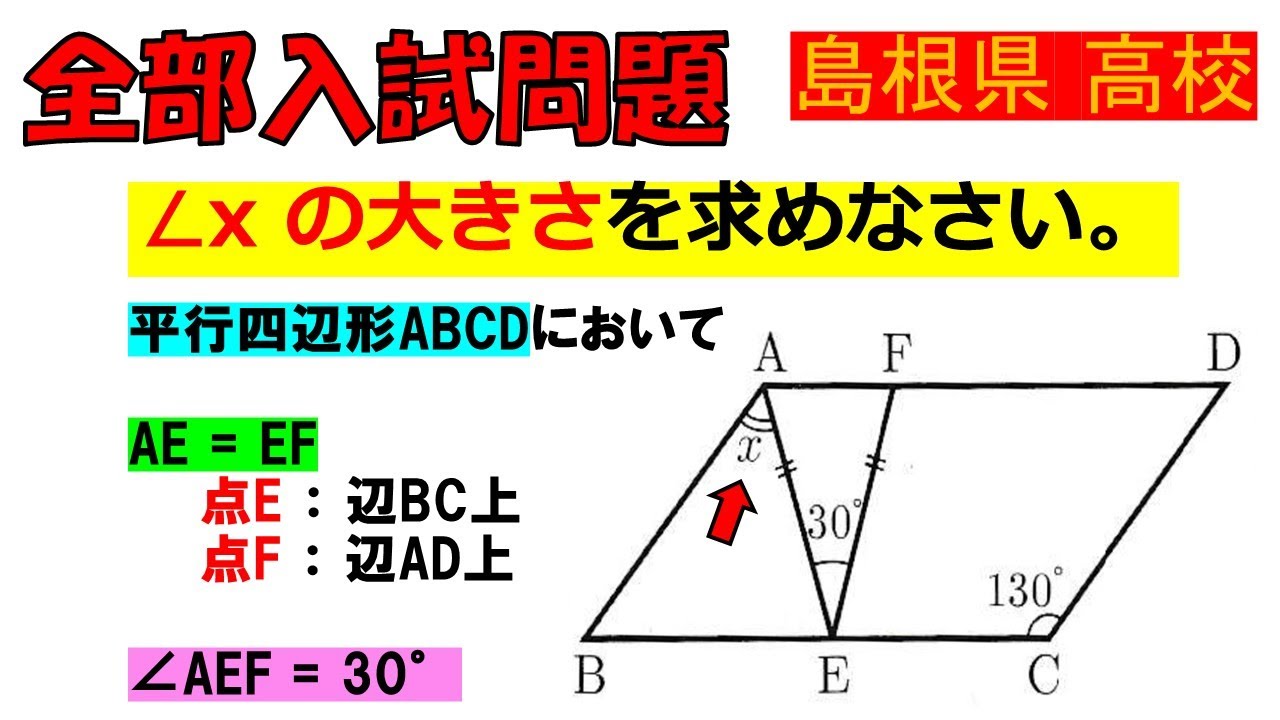
平行四辺形$ABCD$において
$AE=EF$であり,点$E$は辺$BC$上にあり,点$F$は辺$AD$上にある.
$\angle AEF=30°$である.
$\angle x$の大きさを求めなさい.
島根県公立高等学校過去問
この動画を見る
平行四辺形$ABCD$において
$AE=EF$であり,点$E$は辺$BC$上にあり,点$F$は辺$AD$上にある.
$\angle AEF=30°$である.
$\angle x$の大きさを求めなさい.
島根県公立高等学校過去問
30秒で数学の偏差値を4.5上げる動画~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
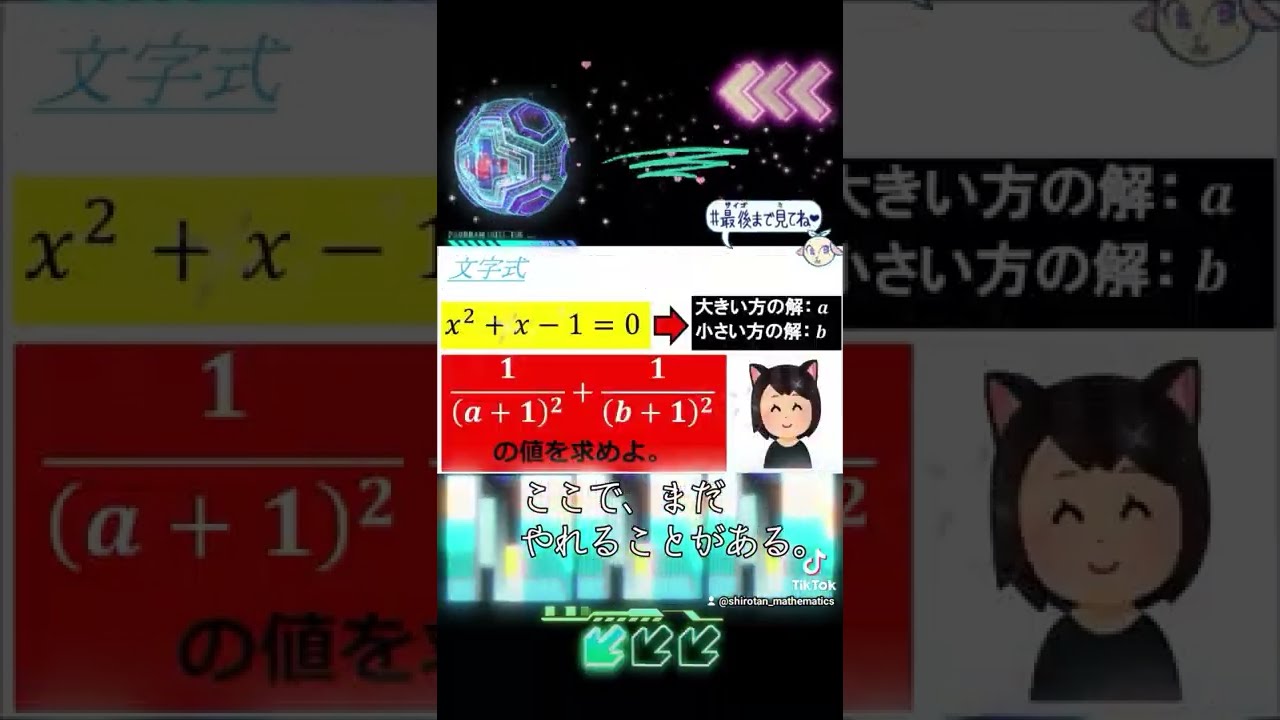
$x^2+x-1=0$の大きい方の解を$a$とし,小さい方の解を$b$とする.
$\dfrac{1}{(a+1)^2}+\dfrac{1}{(b+1)^2}$の値を求めよ.
この動画を見る
$x^2+x-1=0$の大きい方の解を$a$とし,小さい方の解を$b$とする.
$\dfrac{1}{(a+1)^2}+\dfrac{1}{(b+1)^2}$の値を求めよ.
【5分で実力アップ!】確率:向上高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
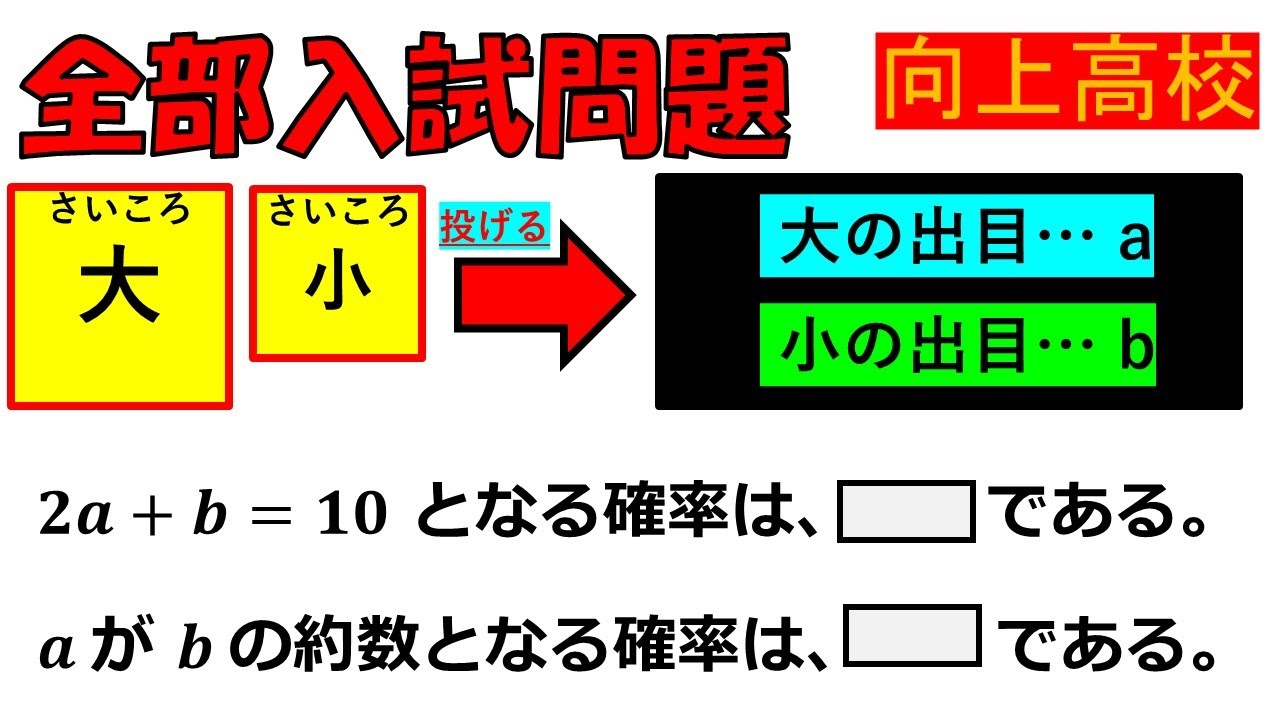
大きいサイコロと小さいサイコロを投げたとき,大の出目を$a$とし,小の出目を$b$とする.
$2a+b=10$となる確率は,$\Box$である.
$a$が$b$の約数となる確率は,$\Box$である.
向上高等学校過去問
この動画を見る
大きいサイコロと小さいサイコロを投げたとき,大の出目を$a$とし,小の出目を$b$とする.
$2a+b=10$となる確率は,$\Box$である.
$a$が$b$の約数となる確率は,$\Box$である.
向上高等学校過去問
【1分で分かる方針!】文章題:向上高等学校~全国入試問題解法

単元:
#数学(中学生)#文章題#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
現在,母の年齢は38歳,姉は13歳,妹は10歳である.
母の年齢が,姉と妹の年齢の和に等しくなるのは,$\Box$年後である.
向上高等学校過去問
この動画を見る
現在,母の年齢は38歳,姉は13歳,妹は10歳である.
母の年齢が,姉と妹の年齢の和に等しくなるのは,$\Box$年後である.
向上高等学校過去問
30秒で数学の基礎を1つ身に付ける相棒~全国入試問題解法 #Shorts #高校入試
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=4(x+2)・・・・① \\
6x-y=-10・・・・②
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=4(x+2)・・・・① \\
6x-y=-10・・・・②
\end{array}
\right.
\end{eqnarray}$
これを解け.
【中学生から理解できる!】三角比(さんかくひ)[ エッセンシャル版 ]:~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三角比に関して解説していきます.
この動画を見る
三角比に関して解説していきます.
15秒で数学の基礎を身に付けるリズム~全国入試問題解法 #Shorts #数学
【気楽にやろう!上手くやろう!】確率:桐朋高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
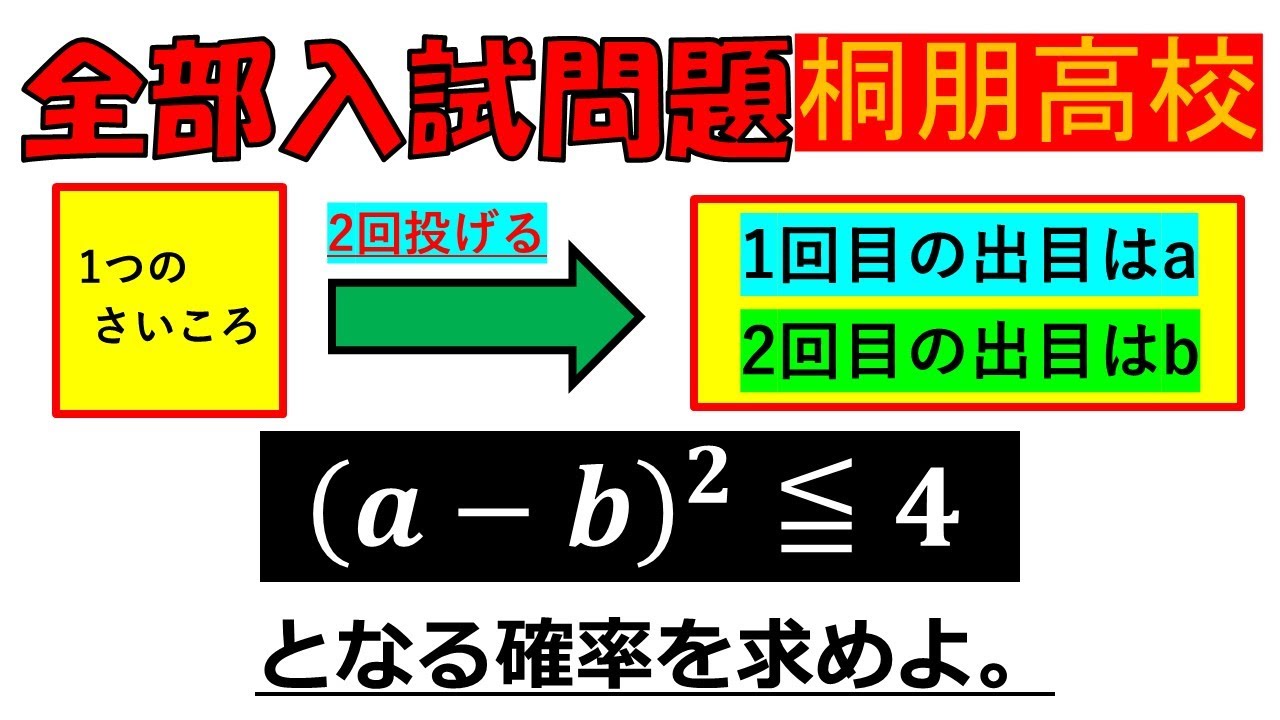
1つのさいころを2回投げるとき,1回目の出目は$a$であり,2回目の出目は$b$である.
$(a-b)^2 \leqq 4$となる確率を求めよ.
桐朋高等学校過去問
この動画を見る
1つのさいころを2回投げるとき,1回目の出目は$a$であり,2回目の出目は$b$である.
$(a-b)^2 \leqq 4$となる確率を求めよ.
桐朋高等学校過去問
【見た目に惑わされないで…】二次方程式:桐朋高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$\dfrac{x^2}{6}-\dfrac{x+5}{3}+\dfrac{1}{2}=0$を解け.
桐朋高等学校過去問
この動画を見る
2次方程式$\dfrac{x^2}{6}-\dfrac{x+5}{3}+\dfrac{1}{2}=0$を解け.
桐朋高等学校過去問
数学のエッセンスを0.5分に詰め込んだ動画~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
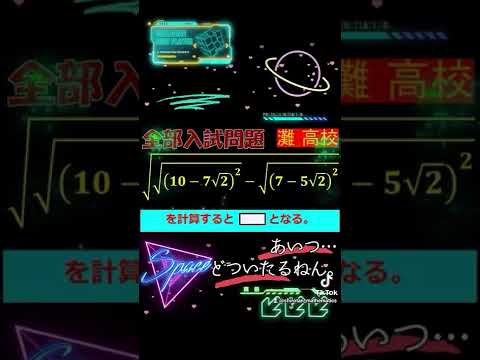
$\sqrt{\sqrt{(10-7\sqrt2)}^2-\sqrt{(7-5\sqrt2)^2}}$の値を求めよ.
この動画を見る
$\sqrt{\sqrt{(10-7\sqrt2)}^2-\sqrt{(7-5\sqrt2)^2}}$の値を求めよ.
【小学校の学習範囲から始まって】整数:市川高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$A-2B-2G+L=2021$のとき,自然数の組$(A,B)$をすべて求めよ.
※$G$は1でない自然数とする.
市川高校過去問
この動画を見る
$A-2B-2G+L=2021$のとき,自然数の組$(A,B)$をすべて求めよ.
※$G$は1でない自然数とする.
市川高校過去問
15秒で数学の1問を身に付ける動画~全国入試問題解法 #Shorts #数学
単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
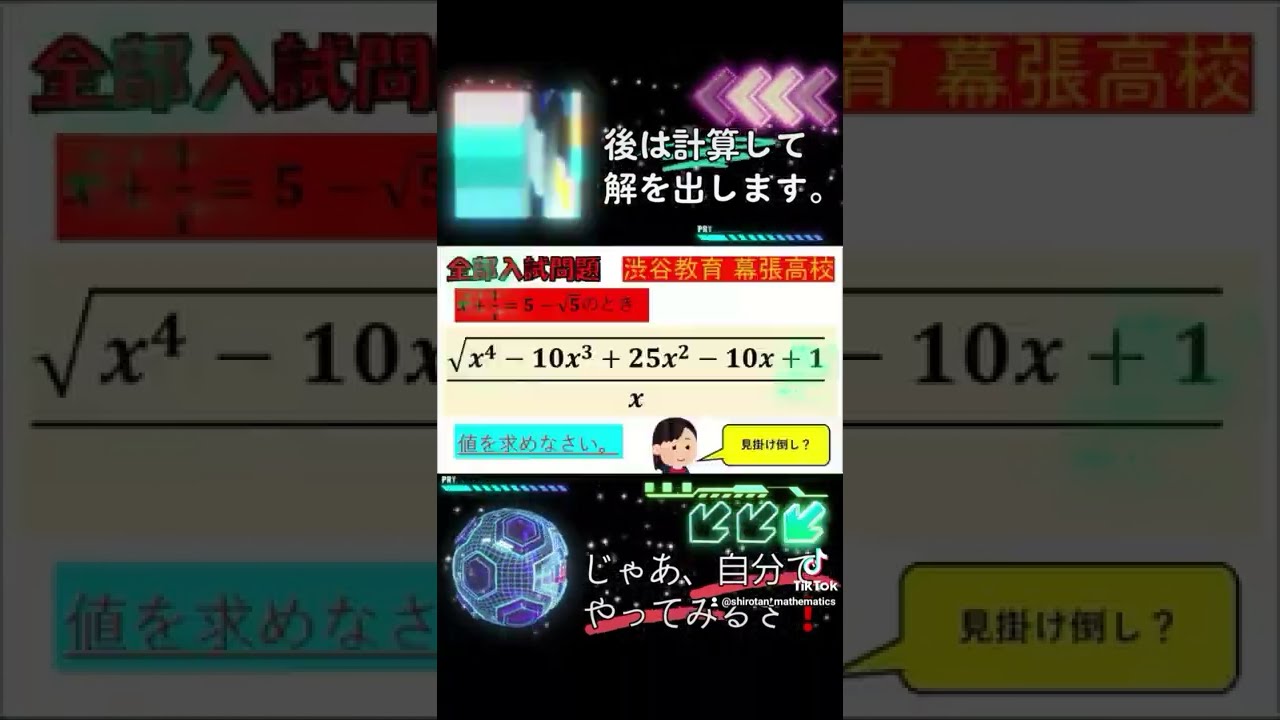
問題文全文(内容文):
$x+\dfrac{1}{x}=5-\sqrt5$のとき,$\dfrac{\sqrt{x^4-10x^3+25x^2-10x+1}}{x}$の値を求めよ.
この動画を見る
$x+\dfrac{1}{x}=5-\sqrt5$のとき,$\dfrac{\sqrt{x^4-10x^3+25x^2-10x+1}}{x}$の値を求めよ.
【…で、実際の解き方は?】二次方程式:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$(2x+3)^2=(3x-8)^2$を解きなさい.
法政大第二高校過去問
この動画を見る
2次方程式$(2x+3)^2=(3x-8)^2$を解きなさい.
法政大第二高校過去問
【無理数とは!】平方根(有理数と無理数)後編:教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根(有理数と無理数)に関して解説していきます.
この動画を見る
平方根(有理数と無理数)に関して解説していきます.



