 数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
割ると余りと商が等しい 2021西大和学園B

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数Nを49で割ったとき商と余りが等しくなった。
このようなNのうち2021より大きいNの個数は?
2021西大和学園高等学校
この動画を見る
自然数Nを49で割ったとき商と余りが等しくなった。
このようなNのうち2021より大きいNの個数は?
2021西大和学園高等学校
角度を求める A A A (清風)
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
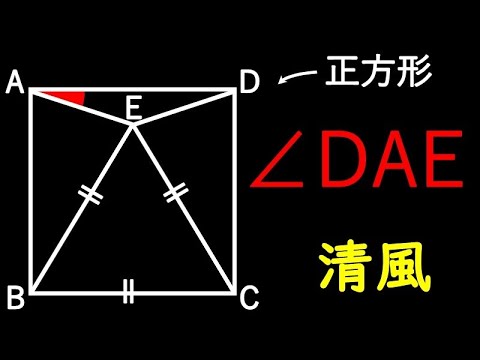
四角形ABCDは正方形
$\angle DAE=?$
*図は動画内参照
横浜清風高等学校
この動画を見る
四角形ABCDは正方形
$\angle DAE=?$
*図は動画内参照
横浜清風高等学校
受験生必見!!円と相似

単元:
#数学(中学生)#中3数学#数A#図形の性質#相似な図形#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円と相似まとめ
*図は動画内参照
この動画を見る
円と相似まとめ
*図は動画内参照
市川 整数 D

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)129と282の最小公倍数は?
(2)自然数A,Bの最大公約数をG、最小公倍数をLとする。
A,BをGで割ったときの商をそれぞれa,bとする。
(ⅰ)Lをa,b,Gで表せ
(ⅱ)A-2B-2G+L=2021のとき(A,B)をすべて求めよ。(G≠1)
2021市川高等学校
この動画を見る
(1)129と282の最小公倍数は?
(2)自然数A,Bの最大公約数をG、最小公倍数をLとする。
A,BをGで割ったときの商をそれぞれa,bとする。
(ⅰ)Lをa,b,Gで表せ
(ⅱ)A-2B-2G+L=2021のとき(A,B)をすべて求めよ。(G≠1)
2021市川高等学校
2021 日大習志野 角の和
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
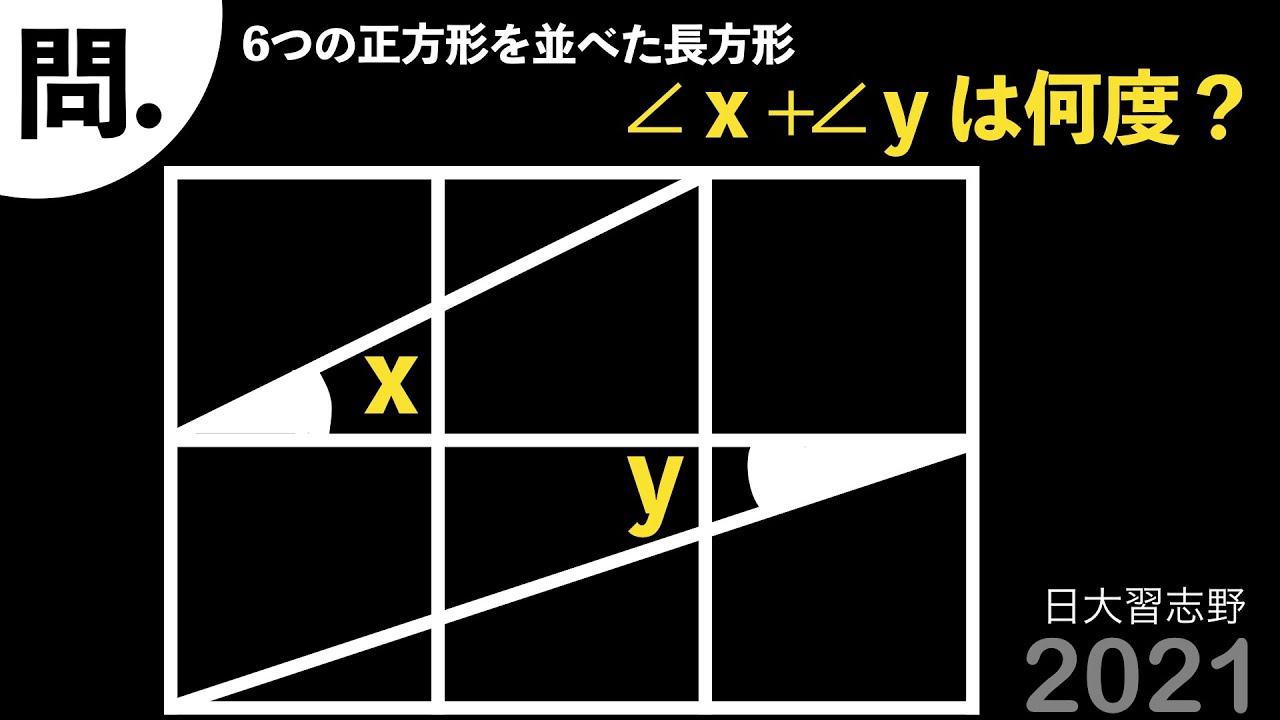
6つの正方形を並べた長方形
$\angle x + \angle y = ?$
2021日本大学習志野高等学校
この動画を見る
6つの正方形を並べた長方形
$\angle x + \angle y = ?$
2021日本大学習志野高等学校
円錐台 内接球 2021 C

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
球を除いた体積=?
*図は動画内参照
2021専修大学松戸高等学校
この動画を見る
球を除いた体積=?
*図は動画内参照
2021専修大学松戸高等学校
2021 平方根と因数分解 A 昭和学院秀英
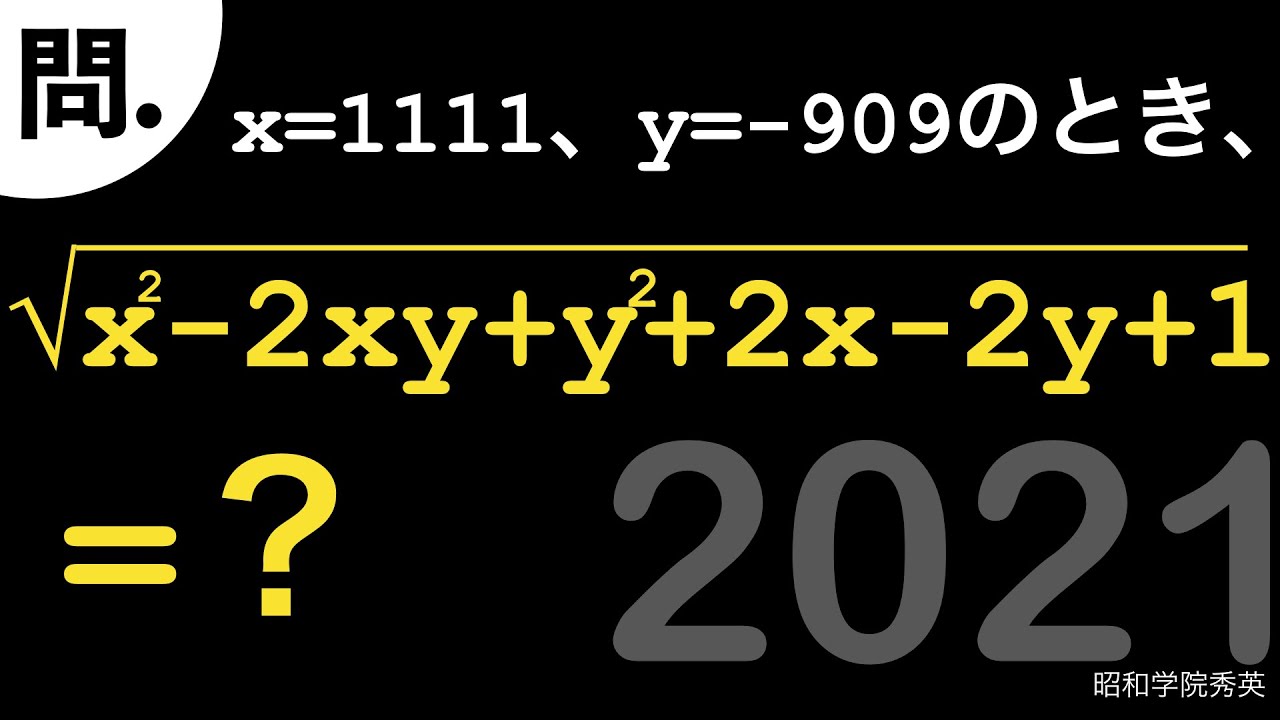
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
x=1111,y=-909のとき
$\sqrt{x^2-2xy+y^2+2x-2y+1} =?$
2021昭和学院秀英高等学校
この動画を見る
x=1111,y=-909のとき
$\sqrt{x^2-2xy+y^2+2x-2y+1} =?$
2021昭和学院秀英高等学校
2021渋谷幕張 円 D
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
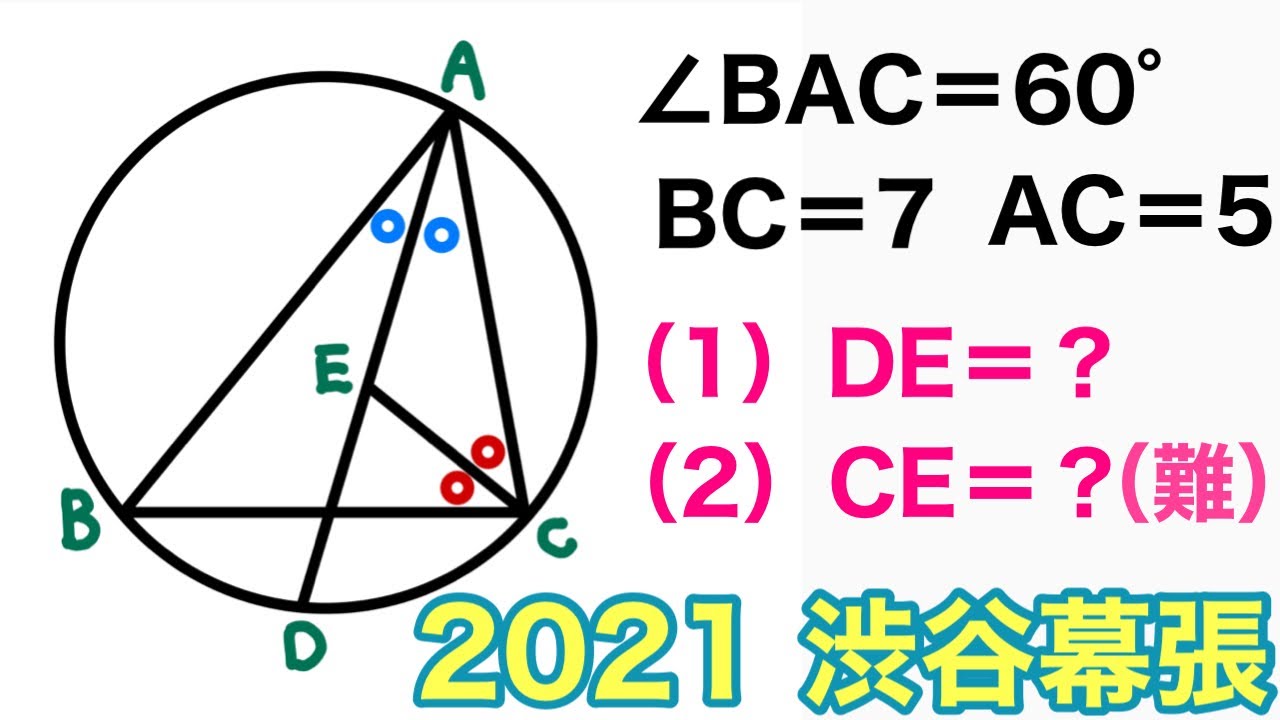
$\angle BAC=60°$
(1)DE=?
(2)CE=?
*図は動画内参照
2021渋谷教育学園幕張高等学校
この動画を見る
$\angle BAC=60°$
(1)DE=?
(2)CE=?
*図は動画内参照
2021渋谷教育学園幕張高等学校
2021昭和学院秀英 確率

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2⃣、3⃣、4⃣、5⃣、6⃣
5枚のカードから無作為に1枚取り出し数字を記録して戻す作業を3回繰り返したとき、記録した数字の積が4の倍数となる確率を求めよ。
2021昭和学院秀英高等学校
この動画を見る
2⃣、3⃣、4⃣、5⃣、6⃣
5枚のカードから無作為に1枚取り出し数字を記録して戻す作業を3回繰り返したとき、記録した数字の積が4の倍数となる確率を求めよ。
2021昭和学院秀英高等学校
2021昭和秀英 正四角錐の外接球
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
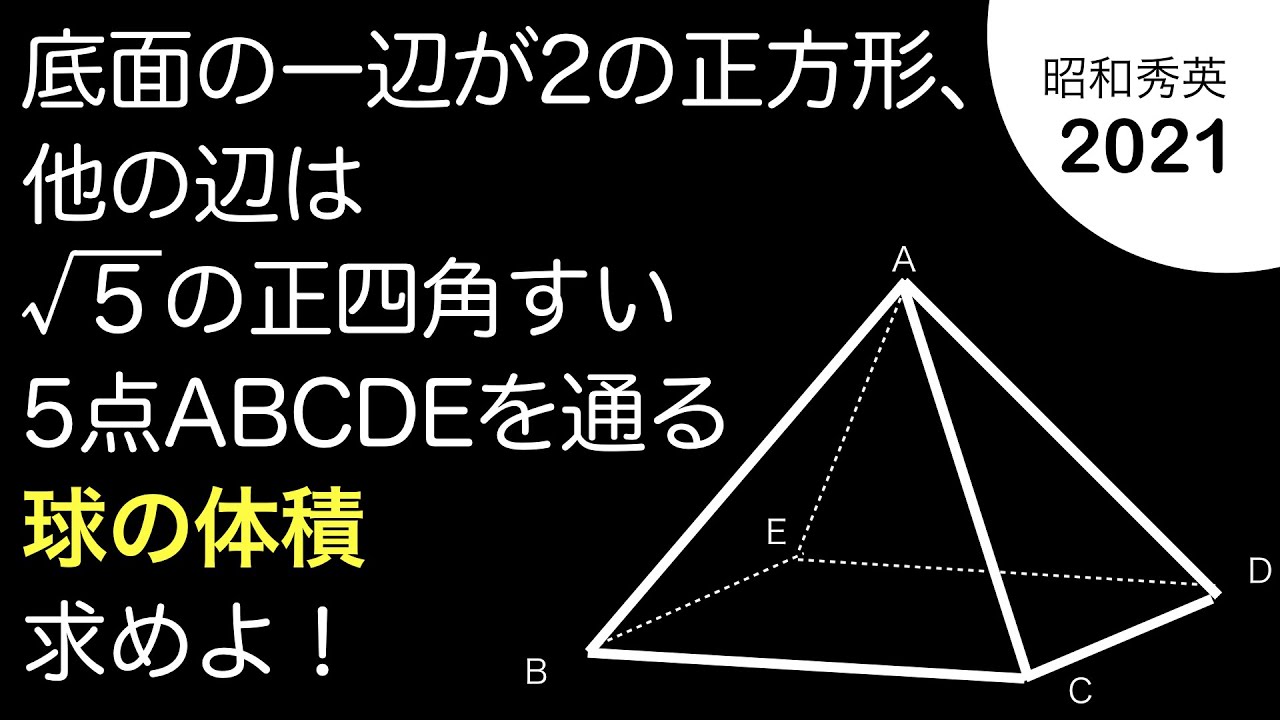
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
*図は動画内参照
2021昭和学院秀英高等学校
この動画を見る
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
*図は動画内参照
2021昭和学院秀英高等学校
瞬殺!!三角形の面積二等分 慶應義塾
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
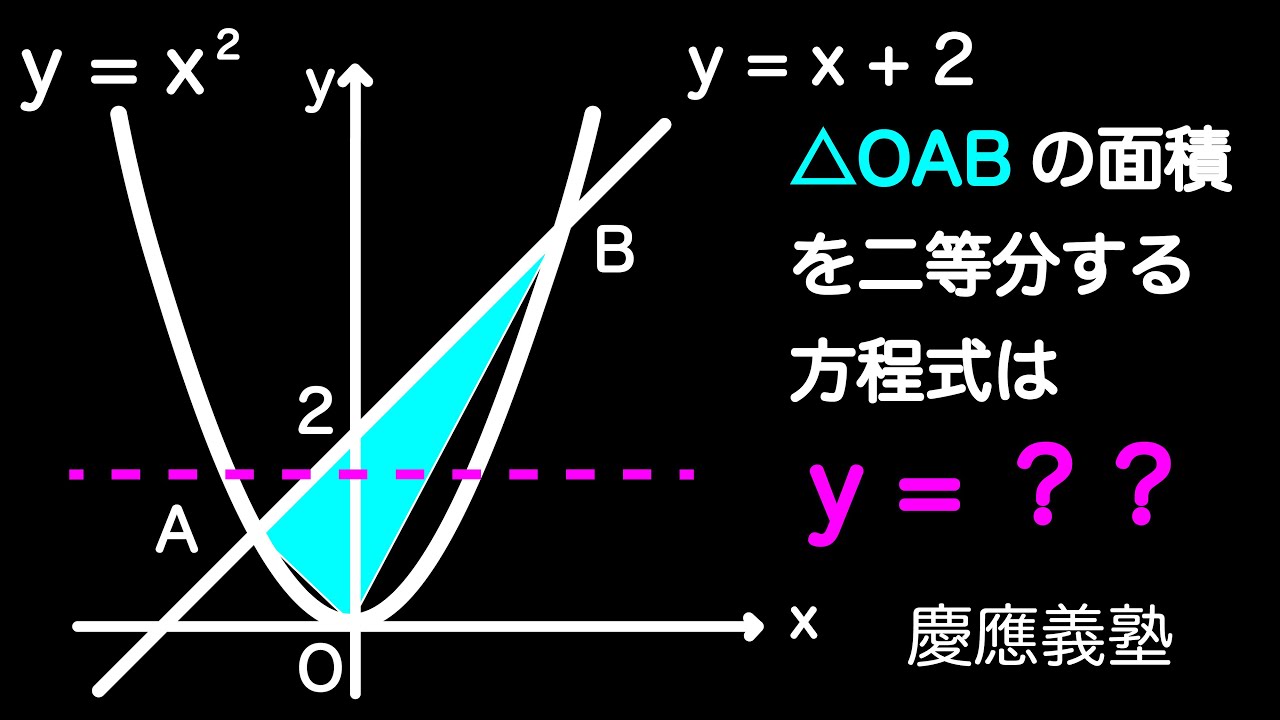
△OABの面積を二等分するx軸に平行な直線の式を求めよ。
*図は動画内参照
慶應義塾高等学校
この動画を見る
△OABの面積を二等分するx軸に平行な直線の式を求めよ。
*図は動画内参照
慶應義塾高等学校
中2も解ける平面図形 C
単元:
#数学(中学生)#平面図形#角度と面積#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
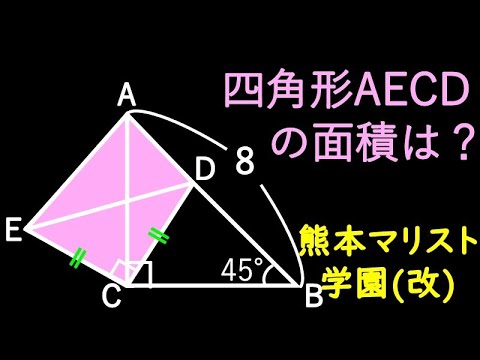
四角形AECDの面積=?
*図は動画内参照
熊本マリスト学園高等学校(改)
この動画を見る
四角形AECDの面積=?
*図は動画内参照
熊本マリスト学園高等学校(改)
一定であることの証明 慶應志木
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
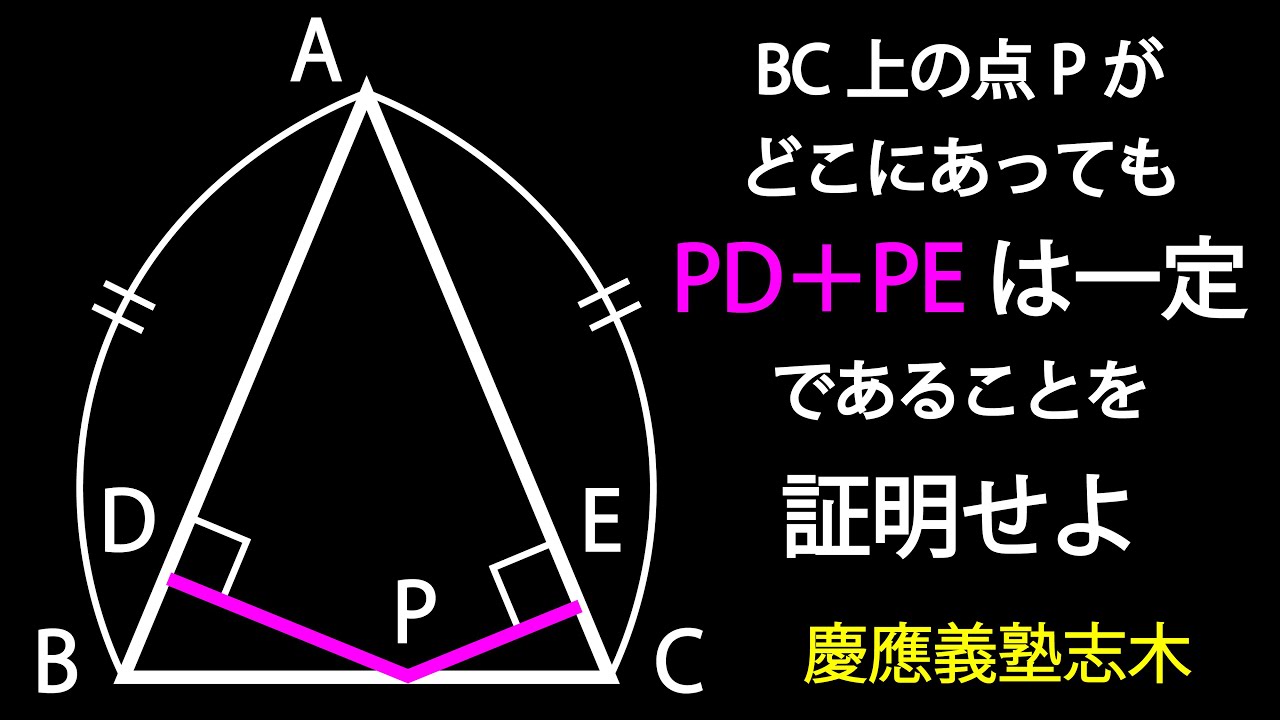
PD+PE=一定であることを証明せよ。
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
PD+PE=一定であることを証明せよ。
*図は動画内参照
慶應義塾志木高等学校
円 三角形の合同の証明 B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
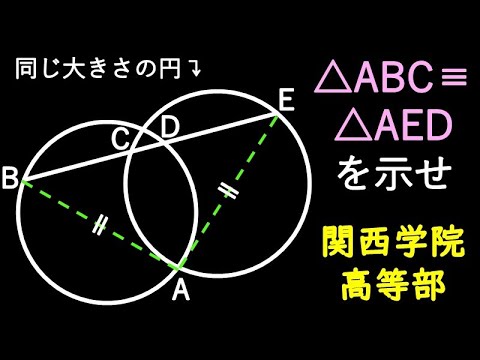
同じ大きさの円
△ABC≡△AEDを示せ
*図は動画内参照
関西学院高等部
この動画を見る
同じ大きさの円
△ABC≡△AEDを示せ
*図は動画内参照
関西学院高等部
函館ラ・サール 面積比
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
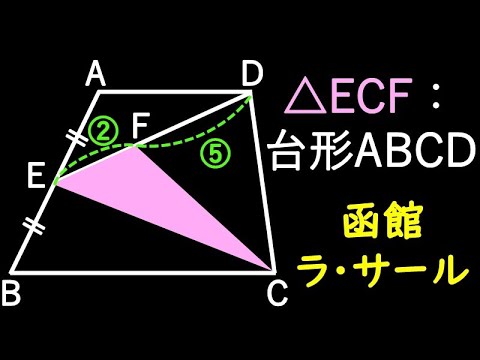
△ECF:台形ABCD=?
*図は動画内参照
函館ラ・サール高等学校
この動画を見る
△ECF:台形ABCD=?
*図は動画内参照
函館ラ・サール高等学校
2次方程式の応用 (灘)C

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a>0 , b>0でaは奇数、bは素数
xの2次方程式
$x^2-ax-b^3=0$が
整数解をもつときa=? b=?
灘高等学校
この動画を見る
a>0 , b>0でaは奇数、bは素数
xの2次方程式
$x^2-ax-b^3=0$が
整数解をもつときa=? b=?
灘高等学校
円 面積最大 角度最大 A
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
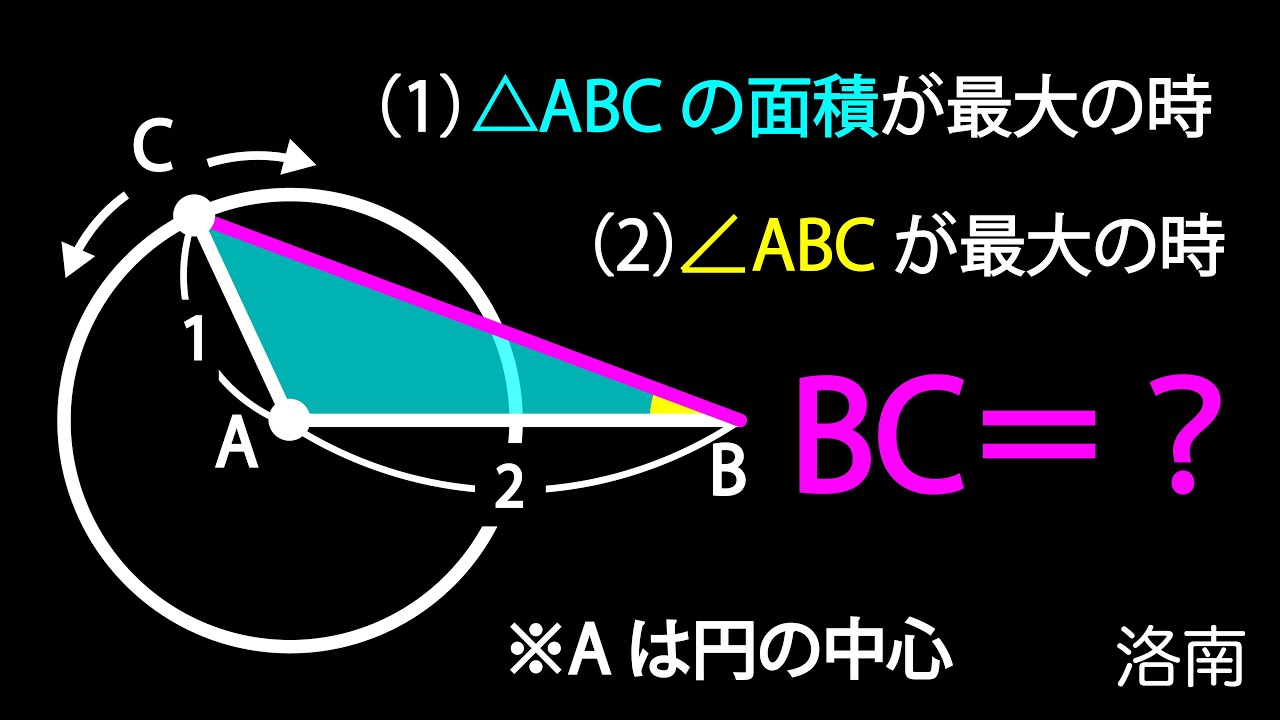
(1)△ABCの面積が最大の時
(2)$\angle ABC$が最大の時
BC=?
*図は動画内参照
洛南高等学校
この動画を見る
(1)△ABCの面積が最大の時
(2)$\angle ABC$が最大の時
BC=?
*図は動画内参照
洛南高等学校
二つの円 角の二等分線 C
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
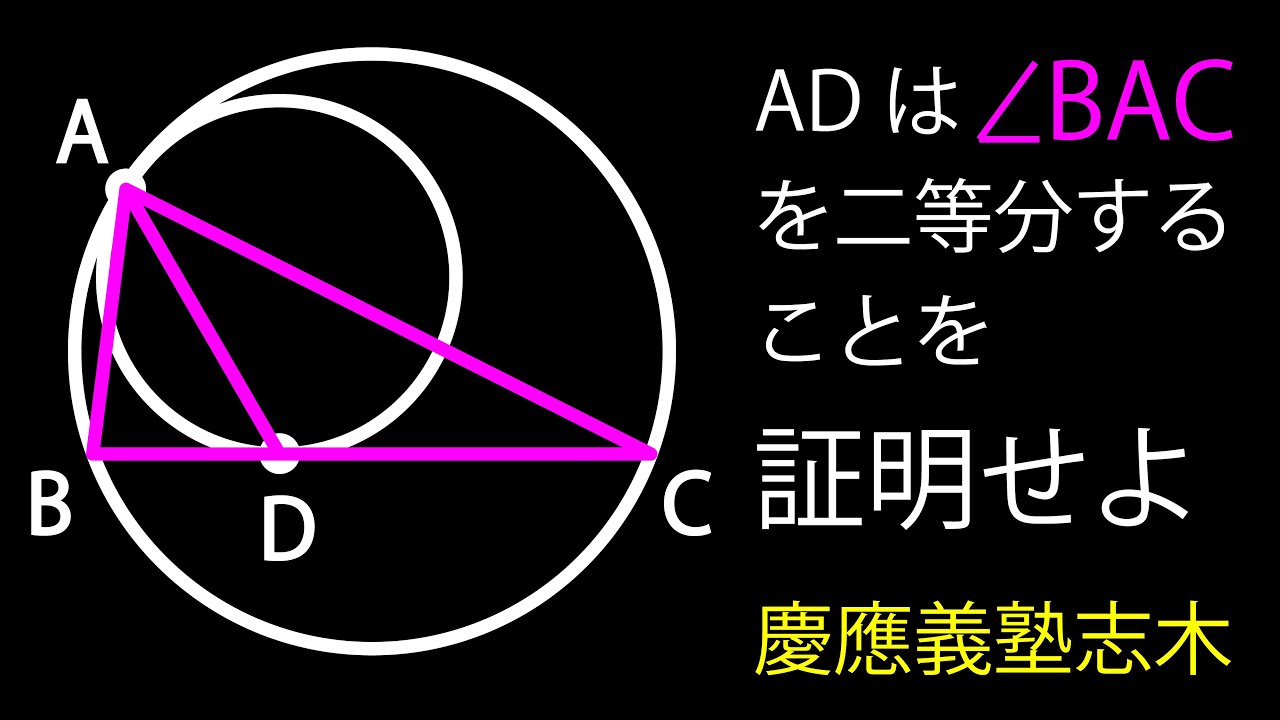
ADは$\angle BAC$を二等分することを示せ
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
ADは$\angle BAC$を二等分することを示せ
*図は動画内参照
慶應義塾志木高等学校
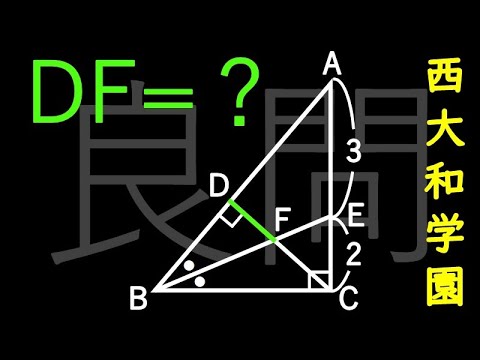
三平方の定理不要! 西大和学園 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DF=?
*図は動画内参照
西大和学園高等学校
この動画を見る
DF=?
*図は動画内参照
西大和学園高等学校
平方根の計算 A コメント欄に良い解説あり!

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{1}{\sqrt 2} - \frac{1}{\sqrt 3})(\frac{1}{\sqrt 6} + \frac{1}{3})=$
日比谷高等学校
この動画を見る
$(\frac{1}{\sqrt 2} - \frac{1}{\sqrt 3})(\frac{1}{\sqrt 6} + \frac{1}{3})=$
日比谷高等学校
整数問題 京都女子
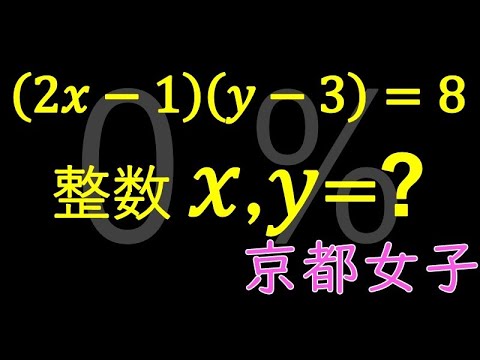
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(2x-1)(y-3) =8$となる整数x、yの値を求めよ。
京都女子高等学校
この動画を見る
$(2x-1)(y-3) =8$となる整数x、yの値を求めよ。
京都女子高等学校
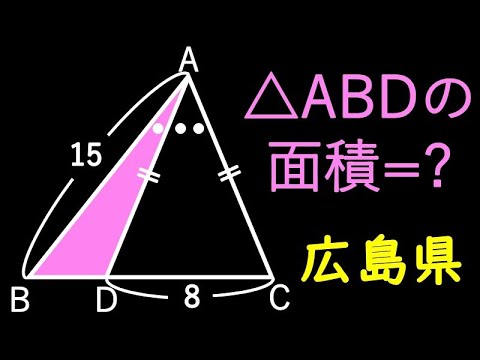
良問!広島県!
等式を満たす2個のサイコロ 確率 立川高校 確率

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
大小2コのサイコロを同時に投げる。
大きいサイコロの目=x
小さいサイコロの目=y
$x^2-6x=y^2-6y$となる確率は?
立川高等学校
この動画を見る
大小2コのサイコロを同時に投げる。
大きいサイコロの目=x
小さいサイコロの目=y
$x^2-6x=y^2-6y$となる確率は?
立川高等学校
素数の二乗の和 B 四天王寺

単元:
#計算と数の性質#数の性質その他#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2+y^2 =365$を満たす素数x,y(x<y)を求めよ。
四天王寺高等学校
この動画を見る
$x^2+y^2 =365$を満たす素数x,y(x<y)を求めよ。
四天王寺高等学校
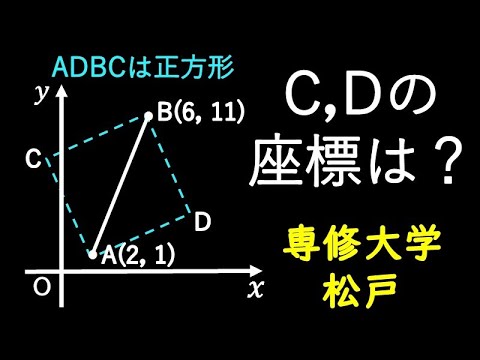
斜めの正方形 B 風車
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
ADBCは正方形
点Cと点Dの座標は?
*図は動画内参照
専修大学松戸高等学校
この動画を見る
ADBCは正方形
点Cと点Dの座標は?
*図は動画内参照
専修大学松戸高等学校
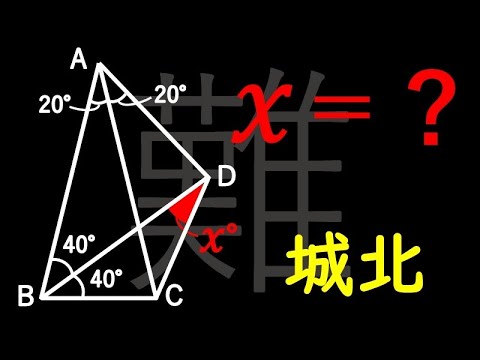
角度 難易度MAX
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x=?$
*図は動画内参照
城北高等学校
この動画を見る
$\angle x=?$
*図は動画内参照
城北高等学校
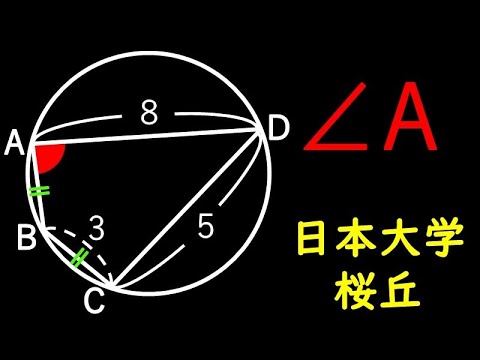
角度を求める C 日大桜ヶ丘
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle A=?$
*図は動画内参照
日本大学櫻丘高等学校
この動画を見る
$\angle A=?$
*図は動画内参照
日本大学櫻丘高等学校
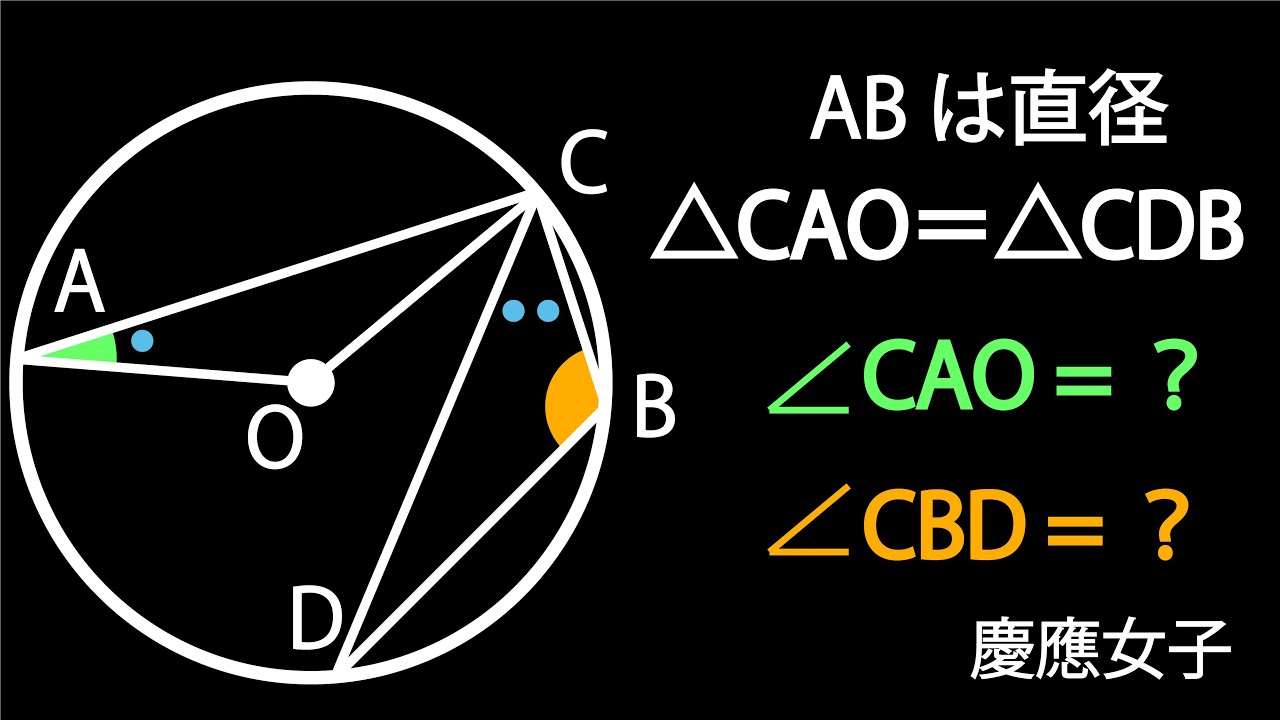
円と角度 慶應女子B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△CAO=△CDB
$\angle CAO = ?$
$\angle CBD = ?$
*図は動画内参照
慶應義塾女子高等学校
この動画を見る
△CAO=△CDB
$\angle CAO = ?$
$\angle CBD = ?$
*図は動画内参照
慶應義塾女子高等学校
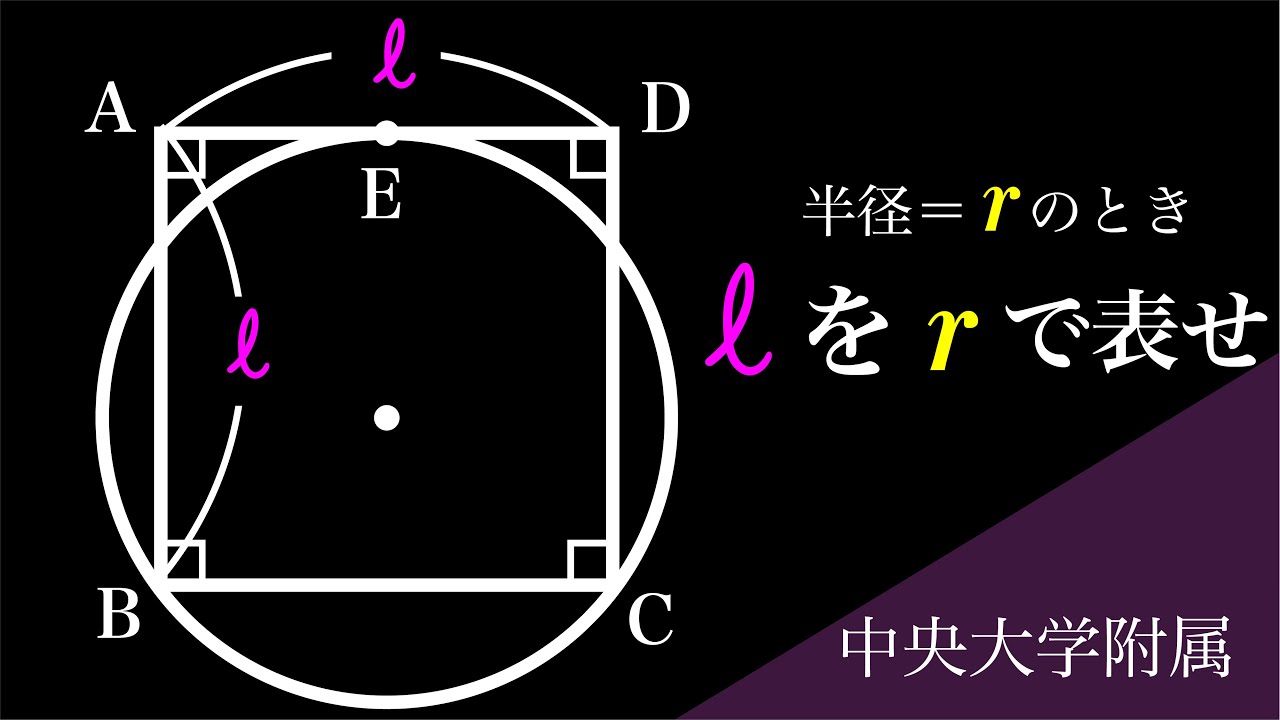
円と三平方 中央大附属 C
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形の1辺の長さ=l
半径=r
lをrで表せ
*図は動画内参照
中央大学附属高等学校
この動画を見る
正方形の1辺の長さ=l
半径=r
lをrで表せ
*図は動画内参照
中央大学附属高等学校
補助線のセンス問われます 円と三平方の定理 中央大附属

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径=2
BH=?
*図は動画内参照
中央大学附属高等学校
この動画を見る
半径=2
BH=?
*図は動画内参照
中央大学附属高等学校





