 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x-5^x=\sqrt{15^x-25^x}$
この動画を見る
実数解を求めよ.
$3^x-5^x=\sqrt{15^x-25^x}$
図形問題 中学生範囲

ドモアブルの定理の証明と応用

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は整数である.
$Z=\sin\theta+i\cos\theta$
$Z^n$を$\cos n\theta$と$\sin n\theta$を用いて表せ.
2021京都工芸大過去問
この動画を見る
$n$は整数である.
$Z=\sin\theta+i\cos\theta$
$Z^n$を$\cos n\theta$と$\sin n\theta$を用いて表せ.
2021京都工芸大過去問
京都工芸繊維大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$m^{m-1}+1$を$8$で割った余りを求めよ.
(1)$m$が偶数のとき
(2)$m$が奇数のとき
2021京都工芸大過去問
この動画を見る
$n$を自然数とする.
$m^{m-1}+1$を$8$で割った余りを求めよ.
(1)$m$が偶数のとき
(2)$m$が奇数のとき
2021京都工芸大過去問
素因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1280000401=p,q$
$p$は3桁であるとき,これを解け.
この動画を見る
$1280000401=p,q$
$p$は3桁であるとき,これを解け.
横浜市立(医)約数・倍数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$A,B$の最大公約数が$G$であり,最小公倍数が$L$である.
$L^2-G^2=72$であるとき,$(A,B)$をすべて求めよ.
2021横浜市立(医)
この動画を見る
自然数$A,B$の最大公約数が$G$であり,最小公倍数が$L$である.
$L^2-G^2=72$であるとき,$(A,B)$をすべて求めよ.
2021横浜市立(医)
綺麗な問題

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の値を求めよ.
$\cos\dfrac{\pi}{33}・\cos\dfrac{2\pi}{33}・\cos\dfrac{4\pi}{33}・\cos\dfrac{8\pi}{33}・\cos\dfrac{16\pi}{33}$
この動画を見る
次の値を求めよ.
$\cos\dfrac{\pi}{33}・\cos\dfrac{2\pi}{33}・\cos\dfrac{4\pi}{33}・\cos\dfrac{8\pi}{33}・\cos\dfrac{16\pi}{33}$
コメント欄の別解は本当にありがたいです

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$16^{\cos^2 x}+16^{\sin^2 x}=10$の別解に関して解説していきます.
この動画を見る
$16^{\cos^2 x}+16^{\sin^2 x}=10$の別解に関して解説していきます.
見掛け倒しの方程式
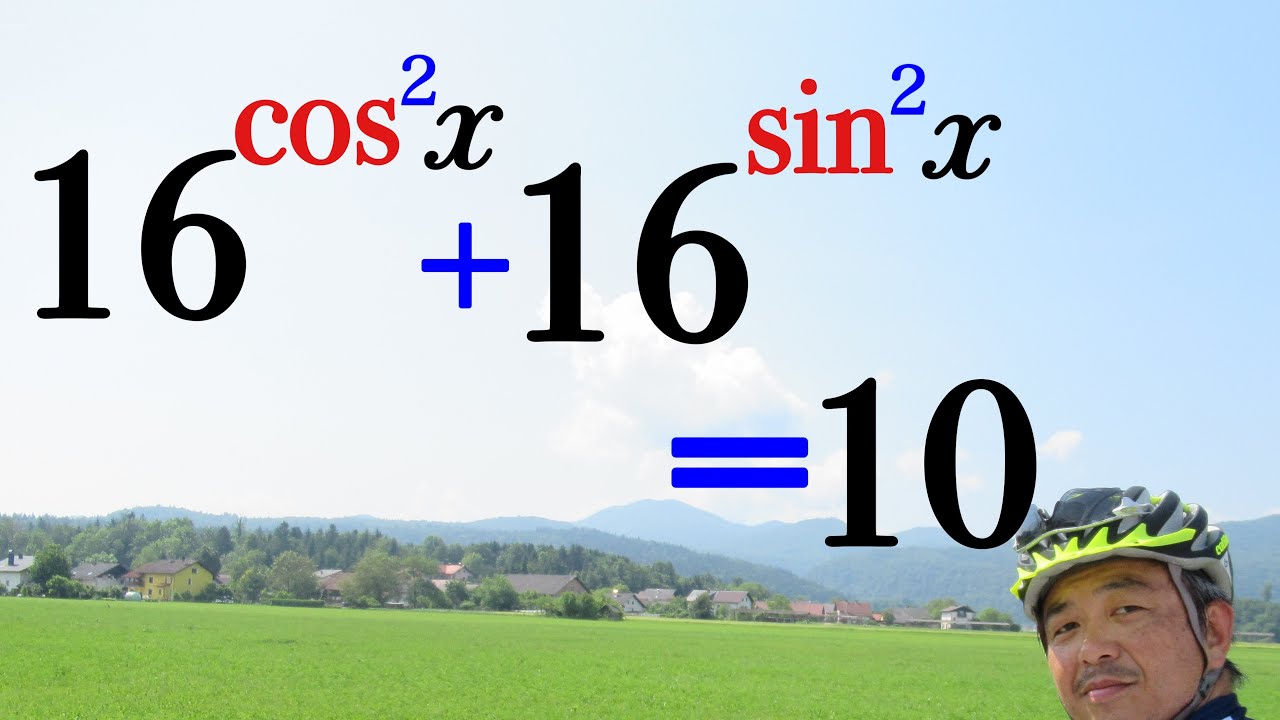
ちょいムズ整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$n$をすべて求めよ.
$\vert 2^n+5^n-65 \vert$が平方数である.
この動画を見る
自然数$n$をすべて求めよ.
$\vert 2^n+5^n-65 \vert$が平方数である.
素数判定 あの定理の証明

三乗根の整数問題

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$(m,n) m\gt 0$をすべて求めよ.
$\sqrt[3]{7+\sqrt m}+\sqrt[3]{7-\sqrt m}=n$
この動画を見る
整数$(m,n) m\gt 0$をすべて求めよ.
$\sqrt[3]{7+\sqrt m}+\sqrt[3]{7-\sqrt m}=n$
ちょっと変わった指数方程式

ただの4次方程式 その2

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$x^4+2x^2-400x=9991$
この動画を見る
これを解け.
$x^4+2x^2-400x=9991$
ただの4次方程式
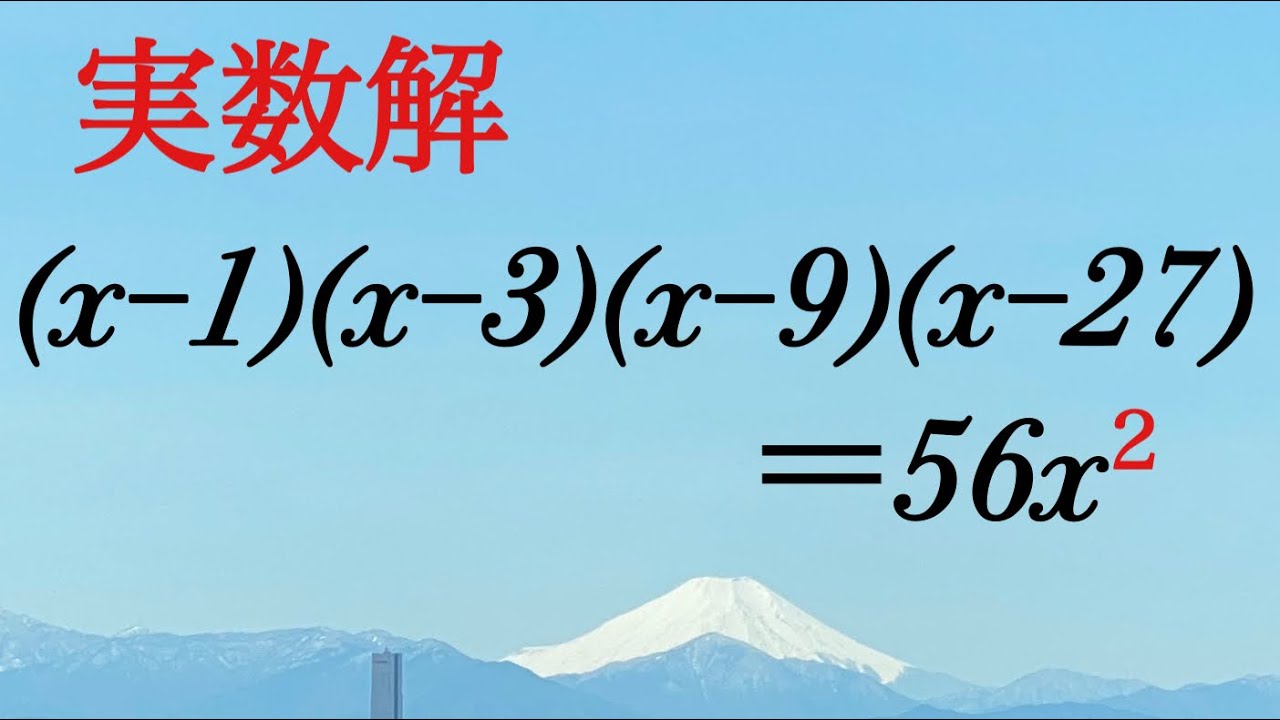
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
この動画を見る
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
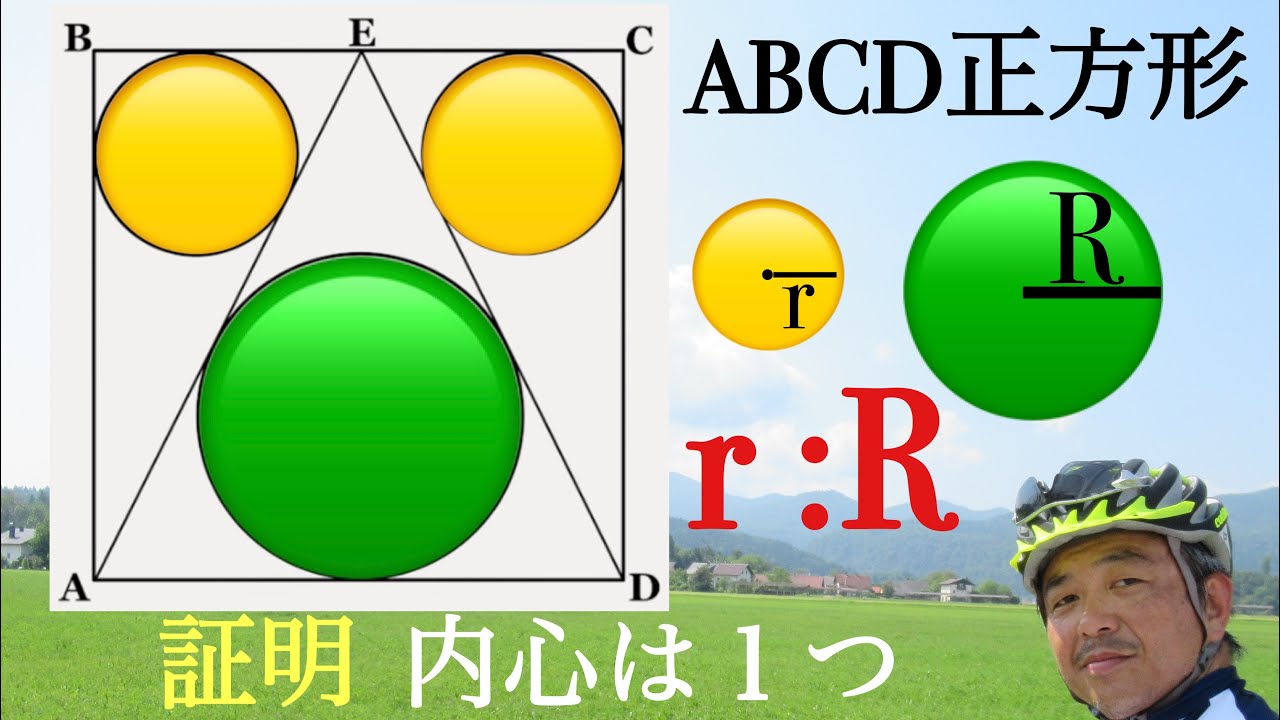
内心 こんなところに黄金比が
2つの解法レピュニット数の和

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
この動画を見る
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
どっちがでかい?
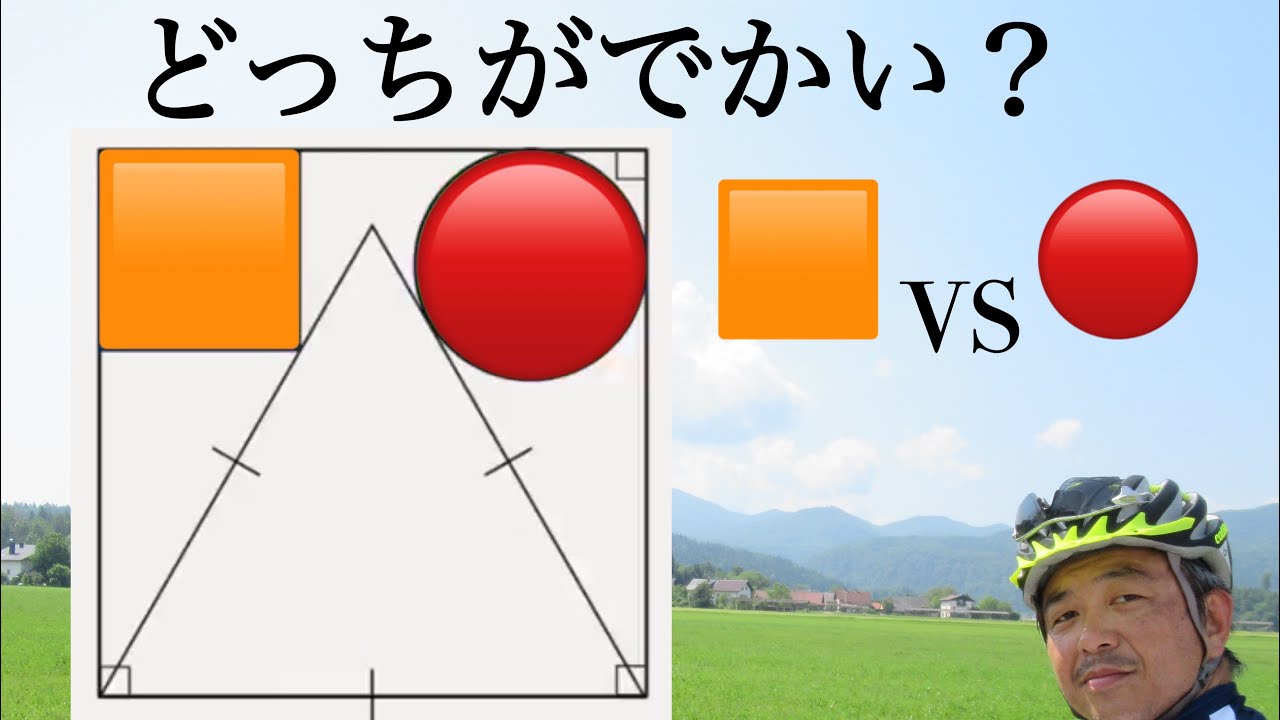
指数不等式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\left(\dfrac{5}{3}\right)^{\frac{x^2+x-3}{x+1}}\leqq \dfrac{2}{3}・\left(\dfrac{5}{2}\right)^{x-\left(\frac{3}{x+1}\right)}$
この動画を見る
これを解け.
$\left(\dfrac{5}{3}\right)^{\frac{x^2+x-3}{x+1}}\leqq \dfrac{2}{3}・\left(\dfrac{5}{2}\right)^{x-\left(\frac{3}{x+1}\right)}$
慶應(理) 関数の極限

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0,e a \fallingdotseq 2.71・・・$
(1)$\sqrt x \log_x \gt -1$を示せ.
(2)(1)を利用して$\displaystyle \lim_{x\to +0} x\log x=0$を示せ.
2019慶應(理)過去問
この動画を見る
$x\gt 0,e a \fallingdotseq 2.71・・・$
(1)$\sqrt x \log_x \gt -1$を示せ.
(2)(1)を利用して$\displaystyle \lim_{x\to +0} x\log x=0$を示せ.
2019慶應(理)過去問
慶應(経済)実数解を持たない4次方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の$4$次方程式が実数解をもたない実数$a$の範囲を求めよ.
$x^4-ax^3+(-2a^2+a+4)x^2+(-2a^2+4a)x$
$+4a=0$
1999慶應(経)
この動画を見る
次の$4$次方程式が実数解をもたない実数$a$の範囲を求めよ.
$x^4-ax^3+(-2a^2+a+4)x^2+(-2a^2+4a)x$
$+4a=0$
1999慶應(経)
愛のある2次方程式

大阪市立大 複素数・整数

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,d$を自然数とする.
$\omega=a-b\sqrt5 i$
$z=c-d\sqrt5 i$
$-\omega z=11+8\sqrt5 i$
$(a,b,c,d)$をすべて求めよ.
2021大阪市立大過去問
この動画を見る
$a,b,c,d$を自然数とする.
$\omega=a-b\sqrt5 i$
$z=c-d\sqrt5 i$
$-\omega z=11+8\sqrt5 i$
$(a,b,c,d)$をすべて求めよ.
2021大阪市立大過去問
ただの不等式

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$30x^2-2・3^{x+1}+19x・3^x \gt 5x^2・3^{x+1}$
$+38x-12$
この動画を見る
これを解け.
$30x^2-2・3^{x+1}+19x・3^x \gt 5x^2・3^{x+1}$
$+38x-12$
またやるの!π>3 05証明 驚愕の解法

早稲田(社)整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$k\geqq 3$を自然数とする.
$2021_{(k)}$を
(1)$k-1$で割り切れる$k$の値を求めよ.
(2)$k+1$で割った余りを$k$で表せ.
(3)$k+2$で割ったら余りが$1$である$k$の値を求めよ.
2021早稲田(社)
この動画を見る
$k\geqq 3$を自然数とする.
$2021_{(k)}$を
(1)$k-1$で割り切れる$k$の値を求めよ.
(2)$k+1$で割った余りを$k$で表せ.
(3)$k+2$で割ったら余りが$1$である$k$の値を求めよ.
2021早稲田(社)
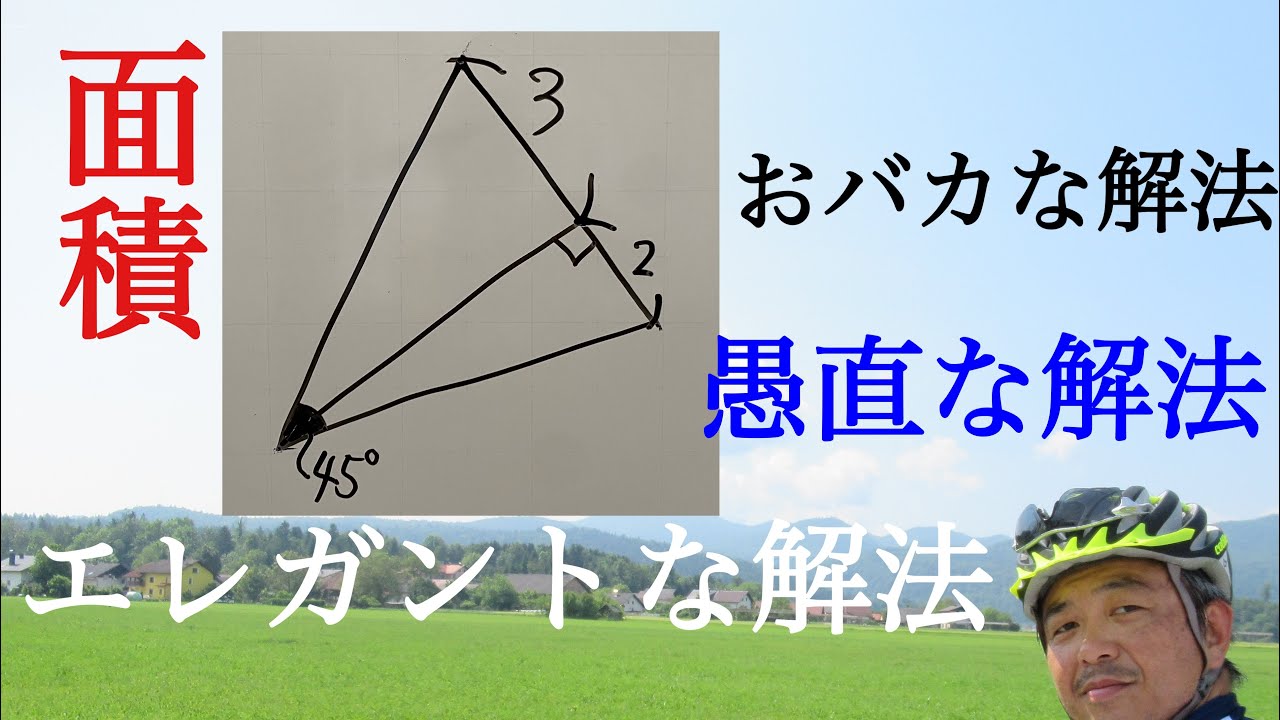
三角形の面積 おバカな解法・愚直な解法・エレガントな解法
立教大 関数の最小値

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$とする.
$\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{2}{x}\right)$の最小値を求めよ.
2021立教大過去問
この動画を見る
$x\gt 0$とする.
$\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{2}{x}\right)$の最小値を求めよ.
2021立教大過去問
聖マリアンナ医大 Σ4乗以上の公式証明

単元:
#数Ⅱ#式と証明#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$\displaystyle \sum_{k=1}^{n}k^3=\left[\dfrac{n(n+1)}{2}\right]$を示せ.
②$(k+1)^5-k^5=5k^4+10k^3+10k^2+5k+1$を利用して
$\displaystyle \sum_{k=1}^{n}k^4$は$n$の5次式で表せることを示せ.
③$\displaystyle \sum_{k=1}^n k^d$は$n$の$(d+1)$次式で表せることを示せ.
2019聖マリアンナ医大過去問
この動画を見る
①$\displaystyle \sum_{k=1}^{n}k^3=\left[\dfrac{n(n+1)}{2}\right]$を示せ.
②$(k+1)^5-k^5=5k^4+10k^3+10k^2+5k+1$を利用して
$\displaystyle \sum_{k=1}^{n}k^4$は$n$の5次式で表せることを示せ.
③$\displaystyle \sum_{k=1}^n k^d$は$n$の$(d+1)$次式で表せることを示せ.
2019聖マリアンナ医大過去問
3通りの解法 首都大

単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\log_{10}x+\log_{10}y=\log_{10}(y+2x^2+1)$
整数$(x,y)$を全て求めよ.
2008首都大過去問
この動画を見る
$\log_{10}x+\log_{10}y=\log_{10}(y+2x^2+1)$
整数$(x,y)$を全て求めよ.
2008首都大過去問



