 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
2021 神戸大(文)複素数の累乗

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$(3+i)^n$
$n=2,3,4,5$の値と虚部の整数を$10$で割った余りを求めよ.
②$(3+i)^n$は虚数であることを示せ.($n$は自然数)
2021神戸大(文)
この動画を見る
①$(3+i)^n$
$n=2,3,4,5$の値と虚部の整数を$10$で割った余りを求めよ.
②$(3+i)^n$は虚数であることを示せ.($n$は自然数)
2021神戸大(文)
cosの積 華麗な解法で綺麗な答え

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\displaystyle \prod_{k=1}^7 \cos\dfrac{\pi}{15}\pi=$
$\cos\dfrac{\pi}{15}\cos\dfrac{2\pi}{15}\cos\dfrac{3\pi}{15}\cos\dfrac{4\pi}{15}\cos\dfrac{5\pi}{15}\cos\dfrac{6\pi}{15}\cos\dfrac{7\pi}{15}$
この動画を見る
これを解け.
$\displaystyle \prod_{k=1}^7 \cos\dfrac{\pi}{15}\pi=$
$\cos\dfrac{\pi}{15}\cos\dfrac{2\pi}{15}\cos\dfrac{3\pi}{15}\cos\dfrac{4\pi}{15}\cos\dfrac{5\pi}{15}\cos\dfrac{6\pi}{15}\cos\dfrac{7\pi}{15}$
方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
この動画を見る
これを解け.$x$を実数とする.
$\sqrt{x^2+3x+2}-\sqrt{x^2+2x+5}=3-x$
なるほど!コメント欄は勉強になります

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1~nの自然数から3つ選ぶ.
3の数のどの2つも連続でない確率を求めよ.
2021近畿大(医)
この動画を見る
1~nの自然数から3つ選ぶ.
3の数のどの2つも連続でない確率を求めよ.
2021近畿大(医)
近畿大(医)確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1~nの自然数から3つ選ぶ.
3の数のどの2つも連続でない確率を求めよ.
2021近畿大(医)
この動画を見る
1~nの自然数から3つ選ぶ.
3の数のどの2つも連続でない確率を求めよ.
2021近畿大(医)
埼玉医科大 確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A,B$交互にサイコロを振り,直前と同じ目が出たら負け,$A$から始めたとき,$B$の負ける確率を求めよ.
2021埼玉医科大過去問
この動画を見る
$A,B$交互にサイコロを振り,直前と同じ目が出たら負け,$A$から始めたとき,$B$の負ける確率を求めよ.
2021埼玉医科大過去問
2021富山大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P\gt 3$,$P$と$P+4$は素数である.
(1)$P$を6で割った余りを示せ.
(2)$P+2$は3の倍数であることを示せ.
(3)$(P+1)(P+2)(P+3)$は$120$の倍数であることを示せ.
2021富山大過去問
この動画を見る
$P\gt 3$,$P$と$P+4$は素数である.
(1)$P$を6で割った余りを示せ.
(2)$P+2$は3の倍数であることを示せ.
(3)$(P+1)(P+2)(P+3)$は$120$の倍数であることを示せ.
2021富山大過去問
富山大 積分のフリしたただの漸化式
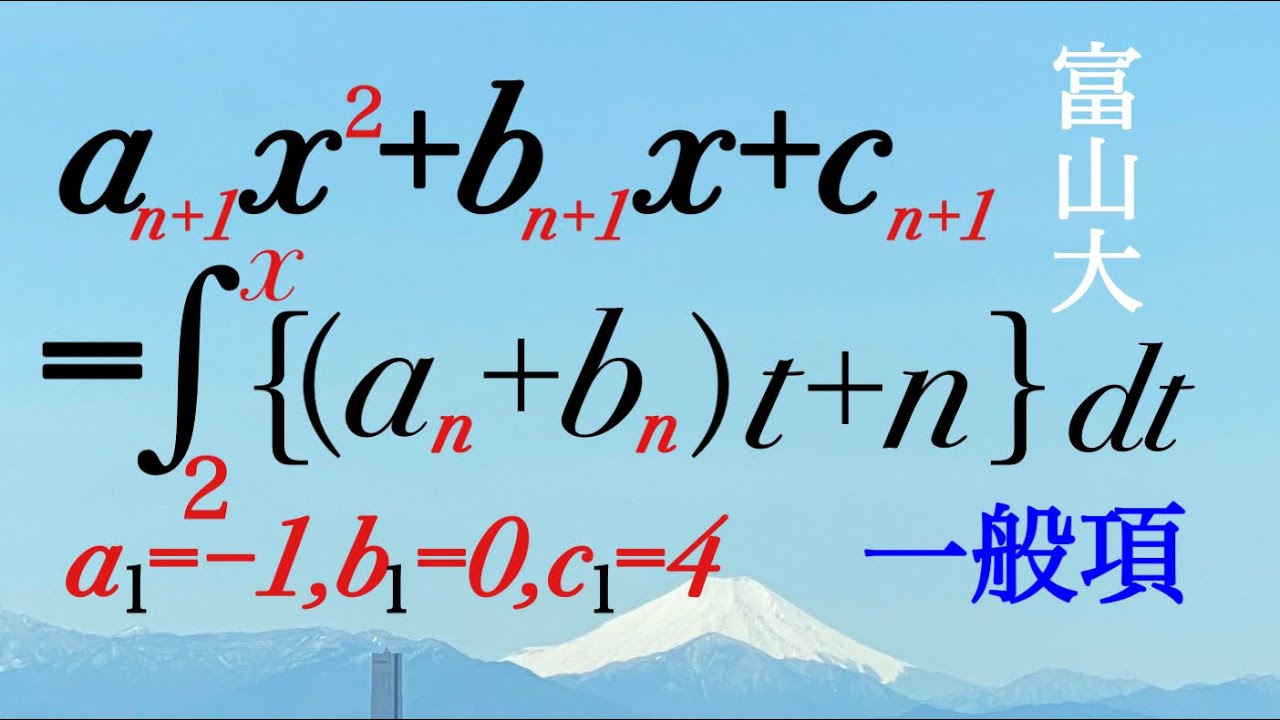
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=-1,b=0,c_1=4$
$a_{n+4}x^2+b_{n+1}x+c_{n+1}=\displaystyle \int_{2}^{x}{(a_n+b_n)t+n}at$
$a_n,b_n,c_n$の一般項を求めよ.
2021富山大過去問
この動画を見る
$a_1=-1,b=0,c_1=4$
$a_{n+4}x^2+b_{n+1}x+c_{n+1}=\displaystyle \int_{2}^{x}{(a_n+b_n)t+n}at$
$a_n,b_n,c_n$の一般項を求めよ.
2021富山大過去問
因数分解&ご報告

ただの因数分解2021関西医科大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$(x^2-15x-2)(x^2+15x-2)-5x^2+2021$
2021関西医科大過去問
この動画を見る
因数分解せよ.
$(x^2-15x-2)(x^2+15x-2)-5x^2+2021$
2021関西医科大過去問
大阪大 積分のフリした整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$を整数とする.
$\displaystyle \int_{a}^{c}(x^2+bx)dx=\displaystyle \int_{b}^{c}(x^2+ax)dx$
①$a\neq b$なら$c$は3の倍数であることを示せ.
②$a\lt b,c=3600$ 整数$(a,b)$は何組であるか?
2021大阪大過去問
この動画を見る
$a,b,c$を整数とする.
$\displaystyle \int_{a}^{c}(x^2+bx)dx=\displaystyle \int_{b}^{c}(x^2+ax)dx$
①$a\neq b$なら$c$は3の倍数であることを示せ.
②$a\lt b,c=3600$ 整数$(a,b)$は何組であるか?
2021大阪大過去問
2021北海道大 連立漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2,b_1=1$
$c_n=a_nb_n$
$a_{n+1}=2a_n+3b_n$
$b_{n+1}=a_n+2b_n$
①$c_2$
②$c_n$は偶数
③$n$が偶数なら$c_n$は28の倍数であることを示せ.
2021北海道大過去問
この動画を見る
$a_1=2,b_1=1$
$c_n=a_nb_n$
$a_{n+1}=2a_n+3b_n$
$b_{n+1}=a_n+2b_n$
①$c_2$
②$c_n$は偶数
③$n$が偶数なら$c_n$は28の倍数であることを示せ.
2021北海道大過去問
答えは0個です。早稲田(商)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021$以下の正の整数で,すべての約数の和が奇数であるものの個数を求めよ.
2021早稲田(商)
この動画を見る
$2021$以下の正の整数で,すべての約数の和が奇数であるものの個数を求めよ.
2021早稲田(商)
2021京都大 整数問題(理系)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3^n-2^n$が素数なら$n$は素数であることを示せ.
2021京都大(理)
この動画を見る
$3^n-2^n$が素数なら$n$は素数であることを示せ.
2021京都大(理)
京都大2021 素数という条件は必要か

2021京都大 秒殺整数問題

頑張って解いてほしい自作問題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\overbrace{111・・・・・・11}^{100桁}$
$243$で割った余りを求めよ.
この動画を見る
$\overbrace{111・・・・・・11}^{100桁}$
$243$で割った余りを求めよ.
どってことない問題

いろいろな方法で解こう

単元:
#数Ⅱ#指数関数と対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(\dfrac{1}{2021}\right)$ VS $\left(\dfrac{1}{2022}\right)^{2021}$
どちらが大きいか?
この動画を見る
$\left(\dfrac{1}{2021}\right)$ VS $\left(\dfrac{1}{2022}\right)^{2021}$
どちらが大きいか?
2021同志社大 4次方程式4つの虚数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
この動画を見る
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
慶応高校 一言言いたいだけの動画

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$(a^2-2a-6)(a^2-2a-17)+18$
2021慶應義塾高過去問
この動画を見る
因数分解せよ.
$(a^2-2a-6)(a^2-2a-17)+18$
2021慶應義塾高過去問
2021早稲田 4次方程式の解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
この動画を見る
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
2021早稲田大 整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-x^2+1$
①$x^6$を$f(x)$で割った余りを求めよ.
②$x^{2021}$を$f(x)$で割った余りを求めよ.
③$(x^2-1)^{3k}-1$は$f(x)$で割り切れることを示せ.$k$は自然数である.
2021早稲田(理)
この動画を見る
$f(x)=x^4-x^2+1$
①$x^6$を$f(x)$で割った余りを求めよ.
②$x^{2021}$を$f(x)$で割った余りを求めよ.
③$(x^2-1)^{3k}-1$は$f(x)$で割り切れることを示せ.$k$は自然数である.
2021早稲田(理)
2021慶應義塾大 整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha^2+3\alpha+3=0$のとき,
(1)$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
(2)$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った商と余りを求めよ.
$(x+1)^{2021}$を$x^2+3x+3$で割った余りを求めよ.
2021慶應(理)
この動画を見る
$\alpha^2+3\alpha+3=0$のとき,
(1)$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
(2)$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った商と余りを求めよ.
$(x+1)^{2021}$を$x^2+3x+3$で割った余りを求めよ.
2021慶應(理)
2021慶應義塾大(理工) 式の値

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha^2+3\alpha+3=0$のとき,$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
2021慶應(理)
この動画を見る
$\alpha^2+3\alpha+3=0$のとき,$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
2021慶應(理)
2021灘高 不思議な誘導付き整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ab^2+(3a+4)b+2a+6=0・・・①$を満たす.
(1)$P=2ab+3a+4$とする.$P^2$を$a$のみを用いて表せ.
(2)①を満たす整数$a,b$を求めよ.$a \neq 0,b \neq 0$
2021灘高過去問
この動画を見る
$ab^2+(3a+4)b+2a+6=0・・・①$を満たす.
(1)$P=2ab+3a+4$とする.$P^2$を$a$のみを用いて表せ.
(2)①を満たす整数$a,b$を求めよ.$a \neq 0,b \neq 0$
2021灘高過去問
明治大 3倍角の公式と3次方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3$倍角の公式を利用して$x^3-3x-1=0$の$3$つの解を$cos$を用いて答えよ.
2020明治大過去問
この動画を見る
$3$倍角の公式を利用して$x^3-3x-1=0$の$3$つの解を$cos$を用いて答えよ.
2020明治大過去問
法政大 複素数の方程式

ざ・見掛け倒し 複素数の基本
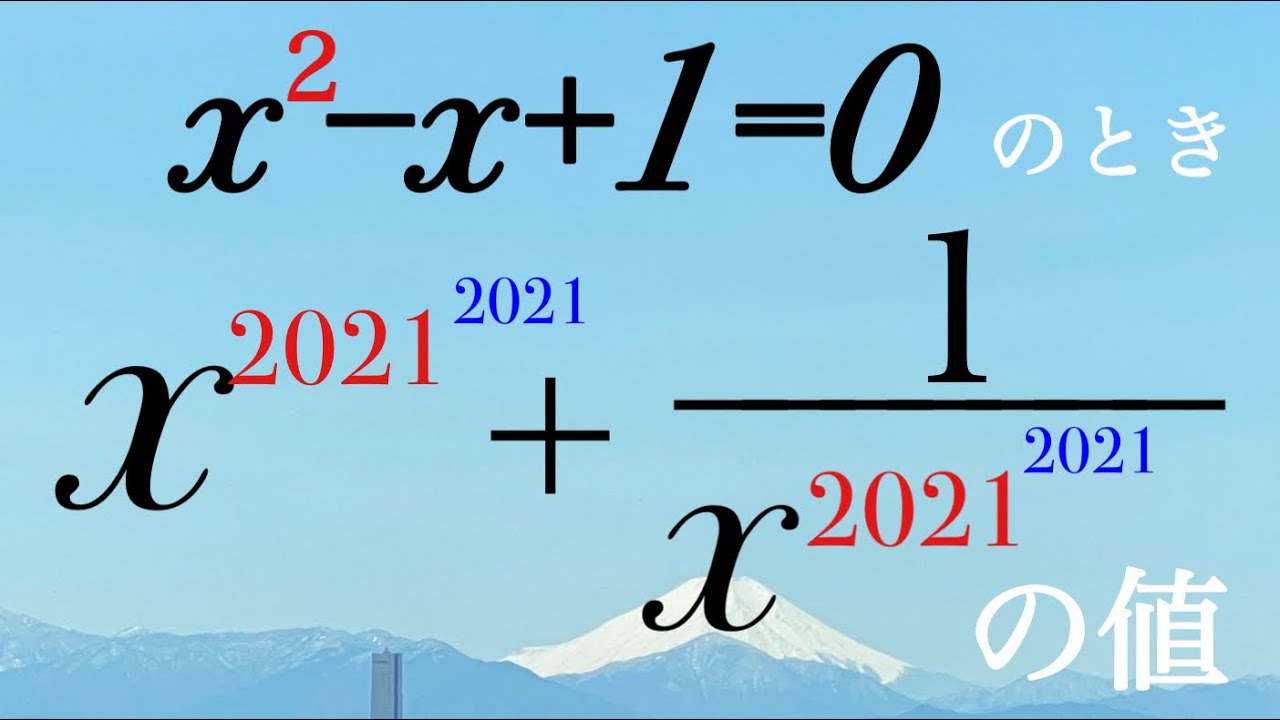
単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-x+1=0$のとき,$x^{2020^{2021}}+\dfrac{1}{x^{2021^{2021}}}$の値を求めよ.
この動画を見る
$x^2-x+1=0$のとき,$x^{2020^{2021}}+\dfrac{1}{x^{2021^{2021}}}$の値を求めよ.
三乗根を外せ (類題)学習院大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
三乗根を外せ.
$\sqrt[3]{9-4\sqrt5}$
この動画を見る
三乗根を外せ.
$\sqrt[3]{9-4\sqrt5}$



