 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
東京都立大

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z^4-2(\cos\displaystyle \frac{3}{7}\pi)z^3+2z^2-2(\cos\displaystyle \frac{3}{7}\pi)z+1=0$
(1)
$z+\displaystyle \frac{1}{z}$の値を求めよ
(2)
$z^n+\displaystyle \frac{1}{z^n}$の実部の最大値とそれを与える自然数$n$を求めよ
出典:東京都立大学 過去問
この動画を見る
$z^4-2(\cos\displaystyle \frac{3}{7}\pi)z^3+2z^2-2(\cos\displaystyle \frac{3}{7}\pi)z+1=0$
(1)
$z+\displaystyle \frac{1}{z}$の値を求めよ
(2)
$z^n+\displaystyle \frac{1}{z^n}$の実部の最大値とそれを与える自然数$n$を求めよ
出典:東京都立大学 過去問
中央大(法)正多角形の内角

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1つの内角の比が$4:5$となる正多角形の組を求めよ
出典:2001年中央大学法学部 過去問
この動画を見る
1つの内角の比が$4:5$となる正多角形の組を求めよ
出典:2001年中央大学法学部 過去問
指数方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
以下を解け
$9^x+15^x=25^x$
この動画を見る
以下を解け
$9^x+15^x=25^x$
成城大 ド・モアブル証明 6倍角の公式?

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#式と証明#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\cos\theta+i\sin\theta$
(1)
$n$整数
$z^n=\cos n \theta + i \sin n \theta$を示せ
(2)
$z+\displaystyle \frac{1}{z}$を$\cos \theta$を用いて表せ
(3)
$\cos^6\theta$を$\cos2\theta,\cos4\theta,\cos6\theta$を用いて表せ
出典:2005年成城大学 過去問
この動画を見る
$z=\cos\theta+i\sin\theta$
(1)
$n$整数
$z^n=\cos n \theta + i \sin n \theta$を示せ
(2)
$z+\displaystyle \frac{1}{z}$を$\cos \theta$を用いて表せ
(3)
$\cos^6\theta$を$\cos2\theta,\cos4\theta,\cos6\theta$を用いて表せ
出典:2005年成城大学 過去問
マイクロソフトの数学部で講師をしてきた。合同式で暗号

芝浦工業大 漸化式 特性方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#漸化式#学校別大学入試過去問解説(数学)#芝浦工業大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=9$
$S_{n+1}=4a_n-10$
一般項$a_n$を求めよ
出典:2005年芝浦工業大学 過去問
この動画を見る
$a_1=9$
$S_{n+1}=4a_n-10$
一般項$a_n$を求めよ
出典:2005年芝浦工業大学 過去問
慶應義塾大(経済)漸化式 特性方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=1$
$a_{n+1}=2a_n^2$
(1)
一般項$a_n$1を求めよ
(2)
$a_n \lt 10^{60}$を満たす最大の$n$
$log_{10}2=0.3010$
出典:2005年慶應義塾大学経済学部 過去問
この動画を見る
$a_1=1$
$a_{n+1}=2a_n^2$
(1)
一般項$a_n$1を求めよ
(2)
$a_n \lt 10^{60}$を満たす最大の$n$
$log_{10}2=0.3010$
出典:2005年慶應義塾大学経済学部 過去問
早稲田大(商)複素数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=(x^2+x+2)^{99}$
$=a_0+a_1x+a_2x^2+a_3x^3+…+a_{198}x^{198}$
$x^2+x+1=0$の1つの解を$\omega$とする
(2)
$f(\omega)$の値を求めよ
(2)
$S=\displaystyle \sum_{k=0}^{66} a_{3k}=a_0+a_3+a_6+…+a_{198}$
出典:1999年早稲田大学 商学部 過去問
この動画を見る
$f(x)=(x^2+x+2)^{99}$
$=a_0+a_1x+a_2x^2+a_3x^3+…+a_{198}x^{198}$
$x^2+x+1=0$の1つの解を$\omega$とする
(2)
$f(\omega)$の値を求めよ
(2)
$S=\displaystyle \sum_{k=0}^{66} a_{3k}=a_0+a_3+a_6+…+a_{198}$
出典:1999年早稲田大学 商学部 過去問
青山学院大 4次関数の接線 積分公式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4+2x^3-3x^2-2x-4$と$y=ax+b$が異なる2点で接している
(1)
$a,b$の値を求めよ
(2)
$f(x)$と$y=ax+b$で囲まれる面積を求めよ
出典:1994年青山学院大学 過去問
この動画を見る
$f(x)=x^4+2x^3-3x^2-2x-4$と$y=ax+b$が異なる2点で接している
(1)
$a,b$の値を求めよ
(2)
$f(x)$と$y=ax+b$で囲まれる面積を求めよ
出典:1994年青山学院大学 過去問
神奈川大 複素数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\displaystyle \frac{1-i}{\sqrt{ 3 }-i})^{12}$
出典:神奈川大学 過去問
この動画を見る
$(\displaystyle \frac{1-i}{\sqrt{ 3 }-i})^{12}$
出典:神奈川大学 過去問
日本大(医学部)複素数
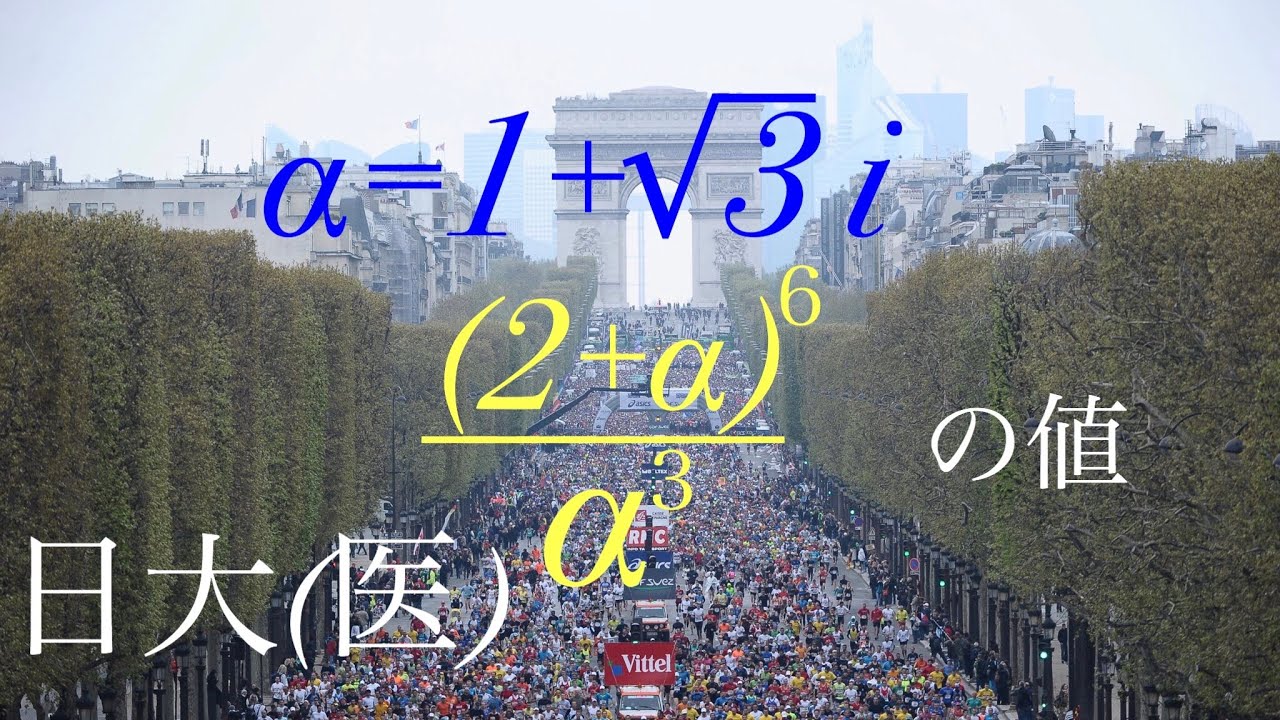
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=1+\sqrt{ 3 }i$
$\displaystyle \frac{(2+\alpha)^6}{\alpha^3}$の値を求めよ
出典:日本大学医学部 過去問
この動画を見る
$\alpha=1+\sqrt{ 3 }i$
$\displaystyle \frac{(2+\alpha)^6}{\alpha^3}$の値を求めよ
出典:日本大学医学部 過去問
日本大(医学部)複素数
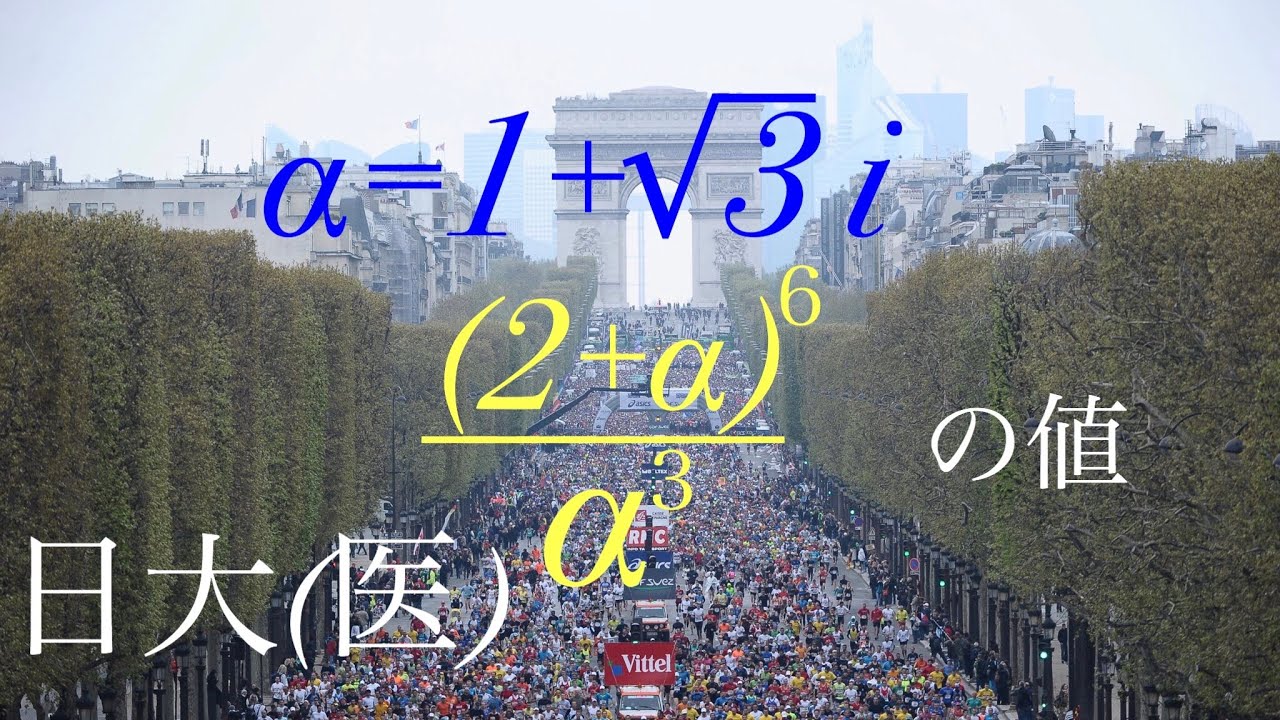
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=1+\sqrt3 i$
$\dfrac{(2+\alpha)^6}{\alpha^3}$の値を求めよ.
日本(医)過去問
この動画を見る
$\alpha=1+\sqrt3 i$
$\dfrac{(2+\alpha)^6}{\alpha^3}$の値を求めよ.
日本(医)過去問
山梨大 複素数
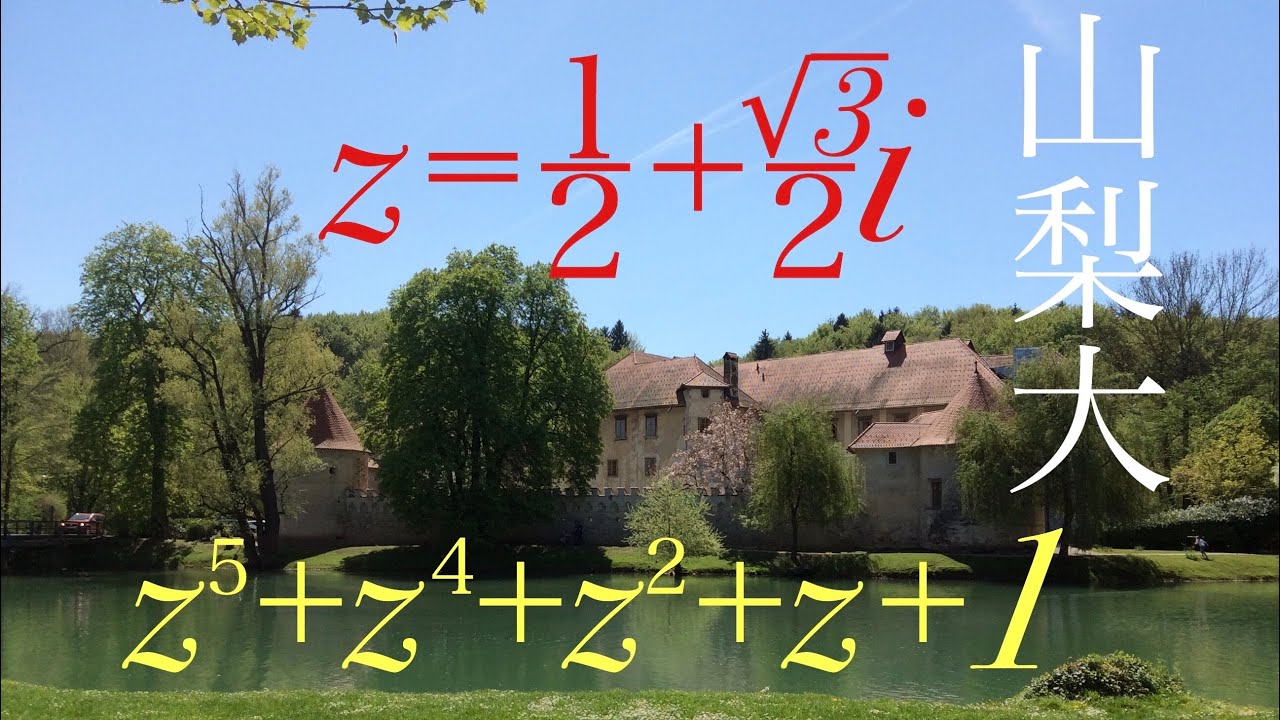
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\displaystyle \frac{1}{2}+\displaystyle \frac{\sqrt{ 3 }}{2}i$
$z^5+z^4+z^2+z+1$の値を求めよ。
出典:山梨大学 過去問
この動画を見る
$z=\displaystyle \frac{1}{2}+\displaystyle \frac{\sqrt{ 3 }}{2}i$
$z^5+z^4+z^2+z+1$の値を求めよ。
出典:山梨大学 過去問
東邦(薬)放物線内の格子点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$自然数
$y=x^2-3x+3n+2$と$y=3nx$とで囲まれた図形の内部(境界線を含む)の格子点の数を求めよ
出典:1994年東邦大学 過去問
この動画を見る
$n$自然数
$y=x^2-3x+3n+2$と$y=3nx$とで囲まれた図形の内部(境界線を含む)の格子点の数を求めよ
出典:1994年東邦大学 過去問
早稲田大 4次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は自然数
$x^4+ax^3+(a+b)x^2+(2-a)x+1=0$
この方程式の解はすべて絶対値が1の複素数である。
$a,b$を求めよ
出典:2003年早稲田大学 過去問
この動画を見る
$a,b$は自然数
$x^4+ax^3+(a+b)x^2+(2-a)x+1=0$
この方程式の解はすべて絶対値が1の複素数である。
$a,b$を求めよ
出典:2003年早稲田大学 過去問
慶應(総合政策)絶対値のついた三次関数の最大最小

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3+3x^2-2$
$|f(-x+2)|$の区間$1 \leqq x \leqq 5$における最大値、最小値を求めよ
出典:2003年慶應義塾大学 過去問
この動画を見る
$f(x)=x^3+3x^2-2$
$|f(-x+2)|$の区間$1 \leqq x \leqq 5$における最大値、最小値を求めよ
出典:2003年慶應義塾大学 過去問
東大 積分 ヨビノリたくみ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0 \leqq t \leqq 2,x^4-2x^2-1+t=0$の実数解のうち
最大のもの:$g_1(t)$
最小のもの:$g_2(t)$
$\displaystyle \int_{0}^{2} (g_1(t)-g_2(t)) dx$
出典:1993年東京大学 過去問
この動画を見る
$0 \leqq t \leqq 2,x^4-2x^2-1+t=0$の実数解のうち
最大のもの:$g_1(t)$
最小のもの:$g_2(t)$
$\displaystyle \int_{0}^{2} (g_1(t)-g_2(t)) dx$
出典:1993年東京大学 過去問
千葉大 三次関数と円 東大数学科卒の杉山さん

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#円と方程式#指数関数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
曲線$y=x^3-x$と円$(x-a^2)+(y-a)^2=2a^2$の共有点が2つ
共有点の$x$座標は?
$(a \gt 0)$
出典:千葉大学 過去問
この動画を見る
曲線$y=x^3-x$と円$(x-a^2)+(y-a)^2=2a^2$の共有点が2つ
共有点の$x$座標は?
$(a \gt 0)$
出典:千葉大学 過去問
もっちゃんと学ぶ 対数 早稲田の過去問もやるよ

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
対数の解説動画です
$15^{50}=??$
出典:早稲田大学 過去問
この動画を見る
対数の解説動画です
$15^{50}=??$
出典:早稲田大学 過去問
青山学院大 関数の最大値・最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x,y)$が次の式を満たすとき
$x^2+y^2-4x-4y+3=0$
$x+2y$の最大値と最小値を求めよ
出典:2003年青山学院大学 過去問
この動画を見る
$(x,y)$が次の式を満たすとき
$x^2+y^2-4x-4y+3=0$
$x+2y$の最大値と最小値を求めよ
出典:2003年青山学院大学 過去問
早稲田(政経)対数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a \gt 0,a \neq 1$ 不等式を解け
$log_a(x+2) \geqq log_{a^2}(3x+16)$
出典:2003年早稲田大学 政治経済学部 過去問
この動画を見る
$a \gt 0,a \neq 1$ 不等式を解け
$log_a(x+2) \geqq log_{a^2}(3x+16)$
出典:2003年早稲田大学 政治経済学部 過去問
学習院大 三次関数と放物線の共通接線の本数

単元:
#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3-x$と$y=x^2+a$の共通接線の数を求めよ
出典:2003年学習院大学 過去問
この動画を見る
$y=x^3-x$と$y=x^2+a$の共通接線の数を求めよ
出典:2003年学習院大学 過去問
東京医科歯科大 整式の大小比較

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は異なる整数
大小比較せよ
(1)
$a^3+b^3,a^2b+ab^2$
(2)
$(a+b+c)(a^2+b^2+c^2)$
$(a+b+c)(ab+bc+ca)$
$3(a^3+b^3+c^3),9abc$
出典:2010年東京医科歯科大学 過去問
この動画を見る
$a,b,c$は異なる整数
大小比較せよ
(1)
$a^3+b^3,a^2b+ab^2$
(2)
$(a+b+c)(a^2+b^2+c^2)$
$(a+b+c)(ab+bc+ca)$
$3(a^3+b^3+c^3),9abc$
出典:2010年東京医科歯科大学 過去問
弘前大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
和が$406$で最小公倍数が$2660$である2つの自然数を求めよ
出典:2010年弘前大学 過去問
この動画を見る
和が$406$で最小公倍数が$2660$である2つの自然数を求めよ
出典:2010年弘前大学 過去問
数学オリンピック予選 整数問題

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$11^{12^{13}}$の十の位
$11$の$12^{13}$乗であり
$11^{12}$の$13$乗ではない
出典:2007年数学オリンピック 予選問題
この動画を見る
$11^{12^{13}}$の十の位
$11$の$12^{13}$乗であり
$11^{12}$の$13$乗ではない
出典:2007年数学オリンピック 予選問題
センター試験(追試)数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$C_1=2$
$C_{n+1}=-C_n+n^2+3$
(1)
$C_{25}-C_{23}$の値を求めよ。
(2)
$C_{25}$の値を求めよ。
出典:2004年センター試験 追試問題
この動画を見る
$C_1=2$
$C_{n+1}=-C_n+n^2+3$
(1)
$C_{25}-C_{23}$の値を求めよ。
(2)
$C_{25}$の値を求めよ。
出典:2004年センター試験 追試問題
名古屋市立大 積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-2x^2$と$y=k$が動画内の図のように交わり$S_1+S_3=S_2$となる。
$k$の値を求めよ。
出典:2001年名古屋市立大学 過去問
この動画を見る
$f(x)=x^4-2x^2$と$y=k$が動画内の図のように交わり$S_1+S_3=S_2$となる。
$k$の値を求めよ。
出典:2001年名古屋市立大学 過去問
漸化式 数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_2=3$
$2S_n=(n+1)a_n-(n-1)$
{$a_n$}の一般項を求めよ
この動画を見る
$a_2=3$
$2S_n=(n+1)a_n-(n-1)$
{$a_n$}の一般項を求めよ
南山大 指数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#南山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x+a・2^{x+1}+b=0$が異なる2つ負の解をもつための$a,b$の満たすべき条件を図示せよ
出典:南山大学 過去問
この動画を見る
$4^x+a・2^{x+1}+b=0$が異なる2つ負の解をもつための$a,b$の満たすべき条件を図示せよ
出典:南山大学 過去問
熊本大 関数の領域

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \geqq x^2-1 \\
y \leqq x+1
\end{array}
\right.
\end{eqnarray}$
$(x,y)$がこの領域を動く
$x^2+y^2-4y$の最大値・最小値を求めよ。
出典:2001年熊本大学 過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \geqq x^2-1 \\
y \leqq x+1
\end{array}
\right.
\end{eqnarray}$
$(x,y)$がこの領域を動く
$x^2+y^2-4y$の最大値・最小値を求めよ。
出典:2001年熊本大学 過去問



