 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
名古屋大 3次式の係数決定

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3+ax^2+bx+c$
$a,b,c$は整数
$f(\sqrt{ 2 })=0$
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$f(w)$は実数
$a,b,c$の値を求めよ
出典:2006年名古屋大学 過去問
この動画を見る
$f(x)=x^3+ax^2+bx+c$
$a,b,c$は整数
$f(\sqrt{ 2 })=0$
$w=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$
$f(w)$は実数
$a,b,c$の値を求めよ
出典:2006年名古屋大学 過去問
東北大 3次方程式 整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-(p-3)x^2-3x+p-1=0$の3つの解がすべて整数となるような実数$p$を求めよ
出典:2000年東北大学 過去問
この動画を見る
$x^3-(p-3)x^2-3x+p-1=0$の3つの解がすべて整数となるような実数$p$を求めよ
出典:2000年東北大学 過去問
早稲田大 整数問題 約数の総積

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$10^n$の正の約数すべての積を求めよ
出典:早稲田大学 過去問
この動画を見る
$10^n$の正の約数すべての積を求めよ
出典:早稲田大学 過去問
北海道大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1つのサイコロを投げ続けて、2回連続して同じ目が出たら終了。
(1)
4回以内(4回を含む)に終わる確率は?
(2)
$r$回以内に終わる確率は?
$(r \geqq 2)$
出典:2006年北海道大学 過去問
この動画を見る
1つのサイコロを投げ続けて、2回連続して同じ目が出たら終了。
(1)
4回以内(4回を含む)に終わる確率は?
(2)
$r$回以内に終わる確率は?
$(r \geqq 2)$
出典:2006年北海道大学 過去問
Entrance exam for Kyoto University.find all $(p,q)$ that meets $p^q+q^p=$prime number.p,q are prime .

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p^q+q^p=$素数を満たすすべての$(p,q)$を見つけてください。($p,q$は素数)
出典:京都大学 入試問題
この動画を見る
$p^q+q^p=$素数を満たすすべての$(p,q)$を見つけてください。($p,q$は素数)
出典:京都大学 入試問題
名古屋大 微分積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=a-(a^3-1)x^2-a^2x^4$ $(a \gt 0)$
(1)
$f(x)$のグラフの概形は?
(2)
$f(x)$と$x$軸とで囲まれる面積を$S(a),\displaystyle \lim_{ a \to \infty }S(a)$
出典:1974年名古屋大学 過去問
この動画を見る
$f(x)=a-(a^3-1)x^2-a^2x^4$ $(a \gt 0)$
(1)
$f(x)$のグラフの概形は?
(2)
$f(x)$と$x$軸とで囲まれる面積を$S(a),\displaystyle \lim_{ a \to \infty }S(a)$
出典:1974年名古屋大学 過去問
横浜市立大(医)
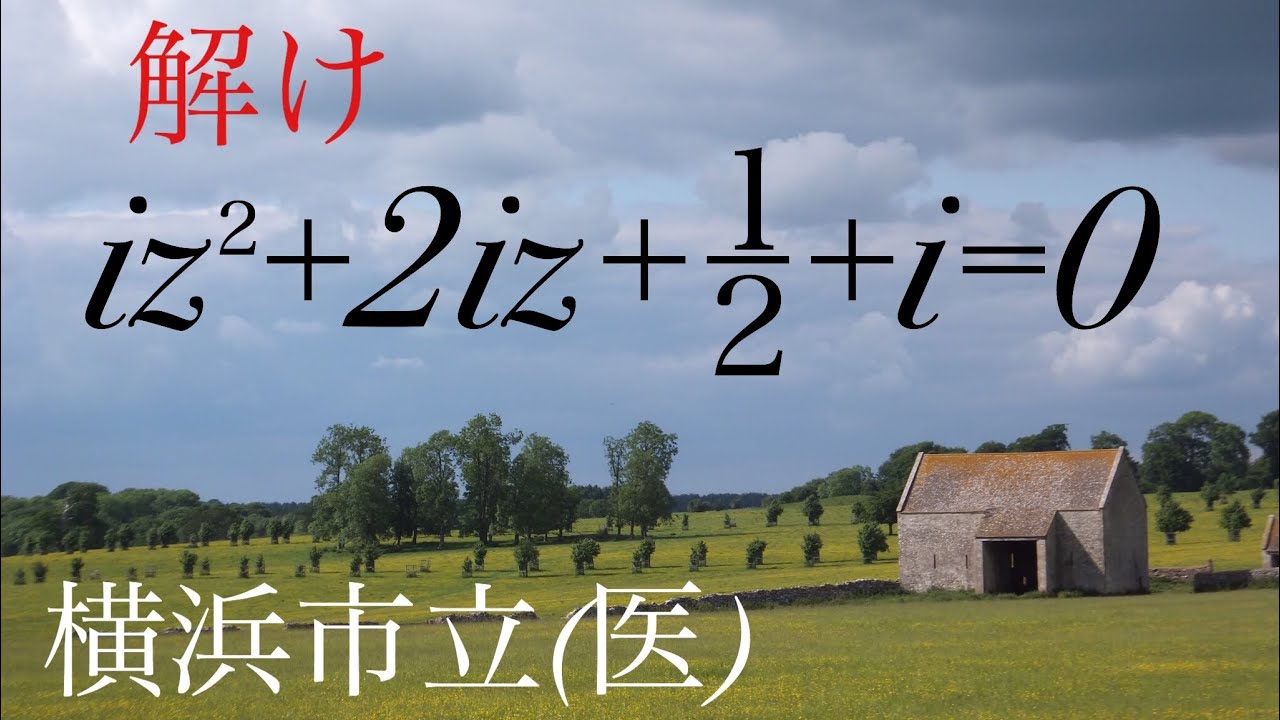
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$iz^2+2iz+\displaystyle \frac{1}{2}+i=0$を解け
出典:2000年横浜市立大学 過去問
この動画を見る
$iz^2+2iz+\displaystyle \frac{1}{2}+i=0$を解け
出典:2000年横浜市立大学 過去問
連続k個の自然数の積はk!の倍数&整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は奇数
$n^5+2n^3-3n$は96の倍数であることを証明せよ
連続$k$個の自然数の積は$k!$の倍数である
この動画を見る
$n$は奇数
$n^5+2n^3-3n$は96の倍数であることを証明せよ
連続$k$個の自然数の積は$k!$の倍数である
京都大 複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{2Z+2i}{Z+2i}=\bar{ Z }$を満たす複素数$Z$をすべて求めよ
出典:2005年京都大学 過去問
この動画を見る
$\displaystyle \frac{2Z+2i}{Z+2i}=\bar{ Z }$を満たす複素数$Z$をすべて求めよ
出典:2005年京都大学 過去問
神戸大 積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
全ての実数$x$で$f(x)=|x^2-1|+\displaystyle \int_{0}^{ 2 } f(x) dx$が成り立つ
(1)
$f(x)$を求めよ
(2)
$\displaystyle \int_{0}^{ a } f(x) dx=\displaystyle \frac{4}{3}$を満たす正の実数$a$
出典:1981年神戸大学 過去問
この動画を見る
全ての実数$x$で$f(x)=|x^2-1|+\displaystyle \int_{0}^{ 2 } f(x) dx$が成り立つ
(1)
$f(x)$を求めよ
(2)
$\displaystyle \int_{0}^{ a } f(x) dx=\displaystyle \frac{4}{3}$を満たす正の実数$a$
出典:1981年神戸大学 過去問
渋谷教育学園幕張高校 税込価格が1万円以下は何通り?

単元:
#数学(中学生)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
鈴木貫太郎
問題文全文(内容文):
1万円以下の税込価格で存在しない価格は何通りか。
税率8%、税抜き価格は自然数。税込み価格は小数点以下は切り捨て
出典:渋谷教育学園幕張高等学校 過去問
この動画を見る
1万円以下の税込価格で存在しない価格は何通りか。
税率8%、税抜き価格は自然数。税込み価格は小数点以下は切り捨て
出典:渋谷教育学園幕張高等学校 過去問
名古屋大 微分 複雑な方程式の解

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$f(x)=x^{-2}2^x$ $(x \neq 0)$
$f'(x) \gt 0$となる条件を求めよ
(2)
$2^x=x^2$実数解の個数を求めよ
(3)
$2^x=x^2$の有理数解をすべて求めよ
出典:2015年名古屋大学 過去問
この動画を見る
(1)
$f(x)=x^{-2}2^x$ $(x \neq 0)$
$f'(x) \gt 0$となる条件を求めよ
(2)
$2^x=x^2$実数解の個数を求めよ
(3)
$2^x=x^2$の有理数解をすべて求めよ
出典:2015年名古屋大学 過去問
福井大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$k,n$は自然数 $a_{1}=k$
$a_{n+1}=2a_{n}+1$
(1)
$a_{n+4}-a_{n}$は15の倍数であることを示せ
(2)
$a_{2010}$が15の倍数となる最小の$k$の値は?
出典:福井大学 過去問
この動画を見る
$k,n$は自然数 $a_{1}=k$
$a_{n+1}=2a_{n}+1$
(1)
$a_{n+4}-a_{n}$は15の倍数であることを示せ
(2)
$a_{2010}$が15の倍数となる最小の$k$の値は?
出典:福井大学 過去問
場合の数 数学オリンピック予選

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#場合の数#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2001$個の自然数$1,2,3…,2001$の中から何個かの数を選ぶ。
選んだ数の総和が奇数となる選び方は何通りか。
(1個も選ばないときの総和は$0$とする。)
出典:数学オリンピック 予選問題
この動画を見る
$2001$個の自然数$1,2,3…,2001$の中から何個かの数を選ぶ。
選んだ数の総和が奇数となる選び方は何通りか。
(1個も選ばないときの総和は$0$とする。)
出典:数学オリンピック 予選問題
早稲田大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_{1}=a,a_{n}=3^n-5a_{n-1}$ $(n \geqq 2)$
(1)
一般項$a_{n}$を求めよ
(2)
任意の自然数$n$に対し、$a_{n+1} \gt a_{n}$が成り立つときの$a$の値を求めよ
出典:2000年早稲田大学 過去問
この動画を見る
$a_{1}=a,a_{n}=3^n-5a_{n-1}$ $(n \geqq 2)$
(1)
一般項$a_{n}$を求めよ
(2)
任意の自然数$n$に対し、$a_{n+1} \gt a_{n}$が成り立つときの$a$の値を求めよ
出典:2000年早稲田大学 過去問
名古屋大 数列 不等式の証明

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_{1}=0,a_{n+1}=\sqrt{ a_{n}^2+5 }-1$ ($n$自然数)
(1)
$0 \leqq a_{n} \lt 2$を示せ
(2)
$a_{n} \lt a_{n+1}$を示せ
出典:名古屋大学 過去問
この動画を見る
$a_{1}=0,a_{n+1}=\sqrt{ a_{n}^2+5 }-1$ ($n$自然数)
(1)
$0 \leqq a_{n} \lt 2$を示せ
(2)
$a_{n} \lt a_{n+1}$を示せ
出典:名古屋大学 過去問
中学入試問題 駒場東邦 整数問題

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#駒場東邦中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$121 \times 122 \times 123 \times 124 \times 125 \times 126 \times 127 \times$
$ 128 \times 129 \times 130$
1の位から順にみて最初に現れる0以外の数字は?
出典:駒場東邦中学校 過去問
この動画を見る
$121 \times 122 \times 123 \times 124 \times 125 \times 126 \times 127 \times$
$ 128 \times 129 \times 130$
1の位から順にみて最初に現れる0以外の数字は?
出典:駒場東邦中学校 過去問
慶應義塾大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_{n}=n3^n_{100}C_{n}$
$b_{n}=n^22^n_{100}C_{n}$
$(n=1,2,3…100)$
(1)
$a_{n}$が最大となる$n$
(2)
$b_{n}$が最大となる$n$
出典:慶應義塾 過去問
この動画を見る
$a_{n}=n3^n_{100}C_{n}$
$b_{n}=n^22^n_{100}C_{n}$
$(n=1,2,3…100)$
(1)
$a_{n}$が最大となる$n$
(2)
$b_{n}$が最大となる$n$
出典:慶應義塾 過去問
南山大 n!0が100個並ぶ

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#南山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n!$は1の位から連続して100個以上の0が並ぶ。
最小の$n$を求めよ。
出典:南山大学 過去問
この動画を見る
$n!$は1の位から連続して100個以上の0が並ぶ。
最小の$n$を求めよ。
出典:南山大学 過去問
名古屋大 双曲線 東大大学院数学科卒 杉山さん

単元:
#大学入試過去問(数学)#平面上の曲線#2次曲線#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=\displaystyle \frac{a^x+a^{-x}}{a^x-a^{-x}}$
$a \gt 0,a \neq 1$
(1)
$f(x)$のとりうる範囲を求めよ
(2)
$f(x)-bx=0$が解をもつ条件を求めよ
出典:1994年名古屋大学 過去問
この動画を見る
$f(x)=\displaystyle \frac{a^x+a^{-x}}{a^x-a^{-x}}$
$a \gt 0,a \neq 1$
(1)
$f(x)$のとりうる範囲を求めよ
(2)
$f(x)-bx=0$が解をもつ条件を求めよ
出典:1994年名古屋大学 過去問
Prove π is larger than 3.05 ~Tokyo University Entrance Examination~

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\pi$が3.05より大きいことを証明せよ
出典:東京大学 入試問題
この動画を見る
$\pi$が3.05より大きいことを証明せよ
出典:東京大学 入試問題
九州大 3次方程式:2次方程式 有理数解

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=\cos20^{ \circ }+i \sin 20^{ \circ }$
$\alpha = Z+\bar{ Z }$←共役な複素数
(1)
$\alpha$が解となる整数係数3次方程式は?
(2)
(1)の3次方程式は、3つの実数解をもち、そのすべては有理数でないことを示せ
(3)
有理数係数の2次方程式で$\alpha$を解に持つものはないことを示せ
出典:2000年九州大学 過去問
この動画を見る
$Z=\cos20^{ \circ }+i \sin 20^{ \circ }$
$\alpha = Z+\bar{ Z }$←共役な複素数
(1)
$\alpha$が解となる整数係数3次方程式は?
(2)
(1)の3次方程式は、3つの実数解をもち、そのすべては有理数でないことを示せ
(3)
有理数係数の2次方程式で$\alpha$を解に持つものはないことを示せ
出典:2000年九州大学 過去問
広島大 対数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$log_{2}3$は無理数、証明せよ
(2)
$p,q$は異なる自然数
$p$ $log_{2}3$と$q$ $log_{2}3$の小数部分は異なる。
証明せよ
(3)
$log_{2}3$の小数第一位の数を求めよ
出典:広島大学 過去問
この動画を見る
(1)
$log_{2}3$は無理数、証明せよ
(2)
$p,q$は異なる自然数
$p$ $log_{2}3$と$q$ $log_{2}3$の小数部分は異なる。
証明せよ
(3)
$log_{2}3$の小数第一位の数を求めよ
出典:広島大学 過去問
東工大 極限 東大大学院 数学科卒 杉山さん

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$自然数
半径$\displaystyle \frac{1}{n}$の円を重ならないように、半径1の円に外接させる。
外接する円の最大個数を$a_{n}$とする。
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{a_{n}}{n}$を求めよ
出典:1992年東京工業大学 過去問
この動画を見る
$n$自然数
半径$\displaystyle \frac{1}{n}$の円を重ならないように、半径1の円に外接させる。
外接する円の最大個数を$a_{n}$とする。
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{a_{n}}{n}$を求めよ
出典:1992年東京工業大学 過去問
福井県立大 不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#福井県立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は正の実数
$\displaystyle \frac{abc}{(ab+1)(bc+1)(ca+1)} \leqq \displaystyle \frac{1}{8}$を証明せよ
等号式立条件も証明せよ
出典:福井県立大学 過去問
この動画を見る
$a,b,c$は正の実数
$\displaystyle \frac{abc}{(ab+1)(bc+1)(ca+1)} \leqq \displaystyle \frac{1}{8}$を証明せよ
等号式立条件も証明せよ
出典:福井県立大学 過去問
中学生向け計算問題 因数分解 暇つぶし

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解
$\sqrt{ 900・901・902・903+1 }$を計算せよ
$(x+1)(x+2)(x+3)(x+4)-3$
この動画を見る
因数分解
$\sqrt{ 900・901・902・903+1 }$を計算せよ
$(x+1)(x+2)(x+3)(x+4)-3$
千葉大 整式
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
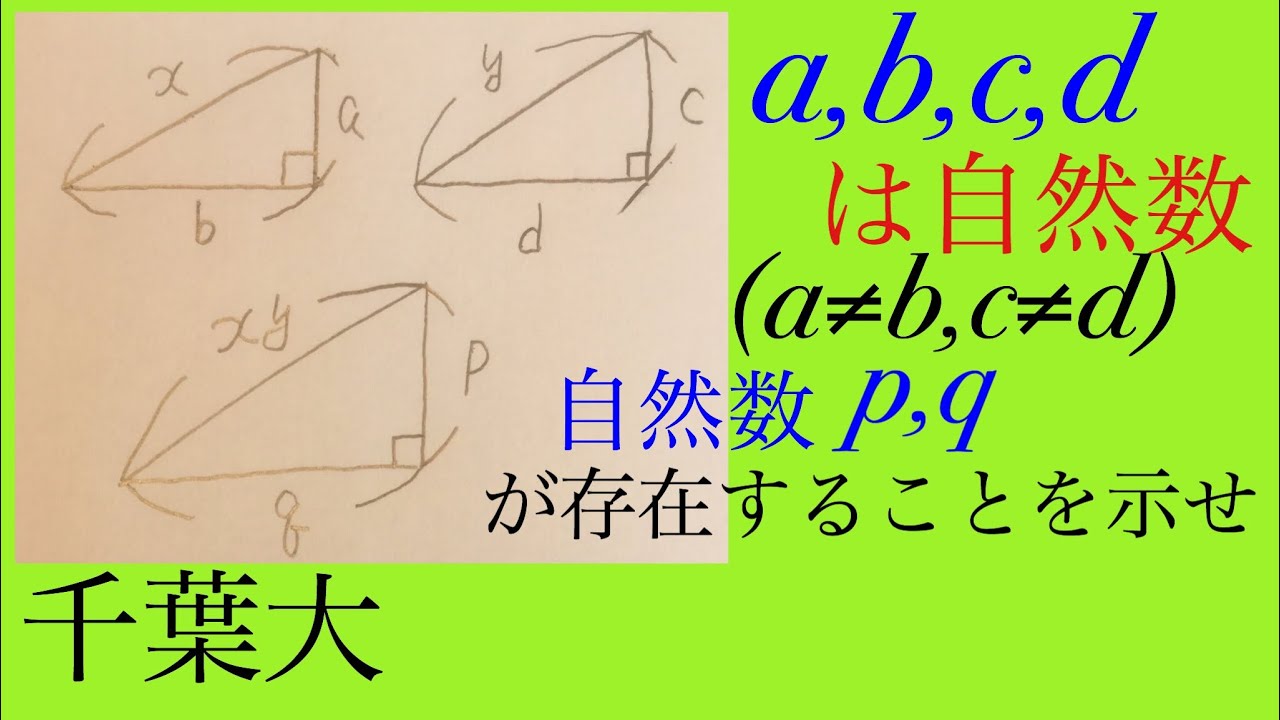
$a,b,c,d$は自然数
$a \neq b,c \neq d$
自然数$p,q$が存在することを示せ
出典:2004年千葉大学 過去問
この動画を見る
$a,b,c,d$は自然数
$a \neq b,c \neq d$
自然数$p,q$が存在することを示せ
出典:2004年千葉大学 過去問
大阪教育大 複雑な3乗根の外し方

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#2次方程式#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }+1 }-\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }-1 }$の値を求めよ
出典:大阪教育大学
この動画を見る
$\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }+1 }-\sqrt[3]{ \sqrt{ \displaystyle \frac{28}{27} }-1 }$の値を求めよ
出典:大阪教育大学
整数問題 合同式 二項展開

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \frac{n^5}{15}+\displaystyle \frac{n^4}{6}+\displaystyle \frac{n^3}{3}+\displaystyle \frac{n^2}{3}+\displaystyle \frac{n}{10}$は$n$が自然数なら自然数であることを示せ
この動画を見る
$\displaystyle \frac{n^5}{15}+\displaystyle \frac{n^4}{6}+\displaystyle \frac{n^3}{3}+\displaystyle \frac{n^2}{3}+\displaystyle \frac{n}{10}$は$n$が自然数なら自然数であることを示せ
早稲田大学 数列、複素数

単元:
#大学入試過去問(数学)#複素数平面#数列#漸化式#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=1+2\sqrt{ 6 }i$
$Z^n=a_{n}+b_{n}i$
(1)
$a_{n}^2+b^2_{n}=5^{2n}$を示せ
(2)
$a_{n+2}=Pa_{n+1}+qa_{n}$ $P,q$の値
(3)
$a_{n}$は5の倍数でないことを示せ
(4)
$Z^n$は実数でないことを示せ
出典:2013年早稲田大学 過去問
この動画を見る
$Z=1+2\sqrt{ 6 }i$
$Z^n=a_{n}+b_{n}i$
(1)
$a_{n}^2+b^2_{n}=5^{2n}$を示せ
(2)
$a_{n+2}=Pa_{n+1}+qa_{n}$ $P,q$の値
(3)
$a_{n}$は5の倍数でないことを示せ
(4)
$Z^n$は実数でないことを示せ
出典:2013年早稲田大学 過去問



