 過去問解説(学校別)
過去問解説(学校別)
 過去問解説(学校別)
過去問解説(学校別)
九九の和わかるかな?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#開智中学
指導講師:
重吉
問題文全文(内容文):
かけ算の九九(一桁の整数のかけ算)81個の数字を全て合計すると▭です。
この動画を見る
かけ算の九九(一桁の整数のかけ算)81個の数字を全て合計すると▭です。
秒で解ける?2025年筑波大附属中「約分」

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#筑波大学附属中学
指導講師:
問題文全文(内容文):
分母と分子の和が860で、約分すると$\dfrac{3}{17}$になる分数を求めなさい。
この動画を見る
分母と分子の和が860で、約分すると$\dfrac{3}{17}$になる分数を求めなさい。
慶應義塾湘南藤沢中等部2025年入試「場合の数」の解説です。

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#慶應義塾湘南藤沢中等部
指導講師:
問題文全文(内容文):
大小2つのサイコロをふって、大きいサイコロの目を十の位、小さくサイコロの目を一の位とする。この二けたの数が3の倍数になるのは▭通りである。
この動画を見る
大小2つのサイコロをふって、大きいサイコロの目を十の位、小さくサイコロの目を一の位とする。この二けたの数が3の倍数になるのは▭通りである。
2025年慶應義塾中等部入試問題算数大問③1,2 中学受験指導歴20年以上のプロ講師解説

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
大問3
(1) [図1]のように、正方形の1辺を延長し、さら
に3本の直線をかき加えました。角xの大きさは▭度です。
※図は動画内参照
(2) [図2] のように、角Aが等しい2つの直角三角形を組み合わせました。四角形 DBCE 面積が 51.48㎤であるとき、三角形ABCの面積は▭㎠です。
この動画を見る
大問3
(1) [図1]のように、正方形の1辺を延長し、さら
に3本の直線をかき加えました。角xの大きさは▭度です。
※図は動画内参照
(2) [図2] のように、角Aが等しい2つの直角三角形を組み合わせました。四角形 DBCE 面積が 51.48㎤であるとき、三角形ABCの面積は▭㎠です。
2025年攻玉社中入試問題算数大問① 中学受験指導歴20年以上のプロ解説!

東大寺学園が書類送検される #shorts

単元:
#算数(中学受験)#数学(中学生)#英語(中学生)#過去問解説(学校別)#高校入試過去問(英語)#高校入試過去問(数学)#東大寺学園中学#東大寺学園高等学校#東大寺学園高等学校
指導講師:
Morite2 English Channel
問題文全文(内容文):
あの**超有名進学校**がまさかの事態に!
高校生クイズでもおなじみの**東大寺学園**と校長たちが、労働基準法違反の容疑で**書類送検**されたぞ。
奈良労働基準監督署の調べによると、2024年10月、教員36人に対し、時間外労働や休日労働をさせたにもかかわらず、**割増賃金約130万円を支払わなかった**疑いが持たれている。
この未払いのほとんどは、**部活動**に関わるものだったという。
しかも、もっとヤバいのは、実は2023年12月に是正勧告が出ていたにもかかわらず、翌年2024年11月の立ち入り調査で**再び不払いが確認された**という事実!どうなってんだ!?
この問題は、残業代がまともに支払われず、**働かせ放題**になっている公立学校の先生たちの労働環境にもつながる、**日本の教育現場の闇**を象徴しているぞ。
この動画を見る
あの**超有名進学校**がまさかの事態に!
高校生クイズでもおなじみの**東大寺学園**と校長たちが、労働基準法違反の容疑で**書類送検**されたぞ。
奈良労働基準監督署の調べによると、2024年10月、教員36人に対し、時間外労働や休日労働をさせたにもかかわらず、**割増賃金約130万円を支払わなかった**疑いが持たれている。
この未払いのほとんどは、**部活動**に関わるものだったという。
しかも、もっとヤバいのは、実は2023年12月に是正勧告が出ていたにもかかわらず、翌年2024年11月の立ち入り調査で**再び不払いが確認された**という事実!どうなってんだ!?
この問題は、残業代がまともに支払われず、**働かせ放題**になっている公立学校の先生たちの労働環境にもつながる、**日本の教育現場の闇**を象徴しているぞ。
2025年慶應義塾中等部入試算数大問② 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
大問1
(1) 太郎君は、所持金の2/9より80円多い金額でノートを買い、次に残りの所持金の2/3より20円少ない金額でペンを買ったところ、180円残りました。太郎君が買ったノートの値段は ▭円です。
(2) 動画内参照
(3) 姉と妹のはじめの所持金の比は3:2でしたが、姉は400円使い、妹は270円もらったので、 姉と妹の所持金の比は2:9になりました。姉のはじめの所持金は▭円です。
(4) 一定の割合で水が入ってくる貯水タンクに、ア. イLの水が入っています。この貯水タンクの水は、毎分150Lの割合でくみ出すとちょうど10分でなくなり、毎分125Lの割合でくみ出すとちょうど18分でなくなります。
(5) 前輪の周の長さが1.7mで、後輪の周の長さが1.2mの自転車があります。この自転車で▭ mの道のりを進むと、後輪が前輪より100回多く回転します。
この動画を見る
大問1
(1) 太郎君は、所持金の2/9より80円多い金額でノートを買い、次に残りの所持金の2/3より20円少ない金額でペンを買ったところ、180円残りました。太郎君が買ったノートの値段は ▭円です。
(2) 動画内参照
(3) 姉と妹のはじめの所持金の比は3:2でしたが、姉は400円使い、妹は270円もらったので、 姉と妹の所持金の比は2:9になりました。姉のはじめの所持金は▭円です。
(4) 一定の割合で水が入ってくる貯水タンクに、ア. イLの水が入っています。この貯水タンクの水は、毎分150Lの割合でくみ出すとちょうど10分でなくなり、毎分125Lの割合でくみ出すとちょうど18分でなくなります。
(5) 前輪の周の長さが1.7mで、後輪の周の長さが1.2mの自転車があります。この自転車で▭ mの道のりを進むと、後輪が前輪より100回多く回転します。
2025年浅野中入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#浅野中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1)動画内参照
(2) 5人の生徒A、B、C、D、Eの身長を調べたところ、Aの身長がもっとも低く、 A、B、C、D、Eの順に高くなっていました。また、DとEの身長の平均はCと Eの身長の平均より5cm高く、CとDの身長の平均は154cmでした。このとき、 Cの身長は イcmです。
また、5人の生徒から2人を選び、2人の身長の平均を求めると、平均が151cm となる組は2組ありました。5人の生徒A、B、C、D、Eの身長の平均は ウcmです。
(3) 西暦の下2桁、月を2桁、日にちを2桁とする6個の数字を順に組み合わせて6 桁の数を作ります。たとえば「西暦2025年2月3日」は「250203」と表されます。 西暦2025年1月1日から西暦2025年12月31日までの365個の6桁の数を考えます。ただし、西暦2025年はうるう年ではありません。
365個の6桁の数の各位の数字の積を考えます。たとえば、「250203」であれば [2 ×5 *×0 *×2 × 0 × 3 = 0]になります。もっとも大きな積は エ であり、積が0となる6桁の数は全部で オ個あります。
(4) 【図1】のような平行四辺形ABCDを、直線ACを軸として1回転させてできる立体の体積はカ cm²、表面積はキ cm²になります。
ただし、円周率は3.14とし、(円すいの体積)=(底面積)×(高さ)×1/3で求められます。
※図は動画内参照
(5) 兄と弟が、2人でいっしょに庭の掃除を始めて、休まずに掃除をし続ければ2時間30分で終わる予定でした。実際には弟が掃除を始め、兄が寝坊して20分遅れて掃除を始めたので、予定より14分長くかかりました。
兄と弟が1時間にする仕事の量の比をもっとも簡単な整数の比で答えるとク : ケです。
もし、2人がいっしょに掃除を始め、兄は「30分掃除をすると10分休むこと」 を繰り返し、弟は休まずに掃除をし続けた場合、掃除が終わるまでコ時間サ分かかります。
この動画を見る
大問1
(1)動画内参照
(2) 5人の生徒A、B、C、D、Eの身長を調べたところ、Aの身長がもっとも低く、 A、B、C、D、Eの順に高くなっていました。また、DとEの身長の平均はCと Eの身長の平均より5cm高く、CとDの身長の平均は154cmでした。このとき、 Cの身長は イcmです。
また、5人の生徒から2人を選び、2人の身長の平均を求めると、平均が151cm となる組は2組ありました。5人の生徒A、B、C、D、Eの身長の平均は ウcmです。
(3) 西暦の下2桁、月を2桁、日にちを2桁とする6個の数字を順に組み合わせて6 桁の数を作ります。たとえば「西暦2025年2月3日」は「250203」と表されます。 西暦2025年1月1日から西暦2025年12月31日までの365個の6桁の数を考えます。ただし、西暦2025年はうるう年ではありません。
365個の6桁の数の各位の数字の積を考えます。たとえば、「250203」であれば [2 ×5 *×0 *×2 × 0 × 3 = 0]になります。もっとも大きな積は エ であり、積が0となる6桁の数は全部で オ個あります。
(4) 【図1】のような平行四辺形ABCDを、直線ACを軸として1回転させてできる立体の体積はカ cm²、表面積はキ cm²になります。
ただし、円周率は3.14とし、(円すいの体積)=(底面積)×(高さ)×1/3で求められます。
※図は動画内参照
(5) 兄と弟が、2人でいっしょに庭の掃除を始めて、休まずに掃除をし続ければ2時間30分で終わる予定でした。実際には弟が掃除を始め、兄が寝坊して20分遅れて掃除を始めたので、予定より14分長くかかりました。
兄と弟が1時間にする仕事の量の比をもっとも簡単な整数の比で答えるとク : ケです。
もし、2人がいっしょに掃除を始め、兄は「30分掃除をすると10分休むこと」 を繰り返し、弟は休まずに掃除をし続けた場合、掃除が終わるまでコ時間サ分かかります。
2025年洗足学園中入試算数大問①、② 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#洗足学園中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1)動画内参照
(2)動画内参照
大問2
(1) 121、 2332、3003のように数字の並び方が右からも左からも同じである数を回文数といいます。4桁の整数で15の倍数である回文数のうち、もっとも大きい数を答えなさい。
(2) 花子さんは90円のボールペンをちょうど何本か買えるお金を持っています。 そのお金で120円のシャープペンを買うと、買える本数は90円のボールペンより 7本少なくなり30円残ります。花子さんが持っているお金はいくらですか。
(3) 川に沿って15km離れたA地点とB地点を船が往復します。この船が川上の B地点からA地点まで下ると2時間かかります。また、A地点からB地点まで上るとき、静水時の速さを1.5倍にすると3時間20分かかります。このとき、川の流れの速さは毎分何mですか。ただし、 静水時の船の速さは一定であるものとします。
(4) 直径12cmの円の周上に円周を12等分する点をとります。色のついた部分の
面積の和は何cmですか。
※図は動画内参照
この動画を見る
大問1
(1)動画内参照
(2)動画内参照
大問2
(1) 121、 2332、3003のように数字の並び方が右からも左からも同じである数を回文数といいます。4桁の整数で15の倍数である回文数のうち、もっとも大きい数を答えなさい。
(2) 花子さんは90円のボールペンをちょうど何本か買えるお金を持っています。 そのお金で120円のシャープペンを買うと、買える本数は90円のボールペンより 7本少なくなり30円残ります。花子さんが持っているお金はいくらですか。
(3) 川に沿って15km離れたA地点とB地点を船が往復します。この船が川上の B地点からA地点まで下ると2時間かかります。また、A地点からB地点まで上るとき、静水時の速さを1.5倍にすると3時間20分かかります。このとき、川の流れの速さは毎分何mですか。ただし、 静水時の船の速さは一定であるものとします。
(4) 直径12cmの円の周上に円周を12等分する点をとります。色のついた部分の
面積の和は何cmですか。
※図は動画内参照
2025年聖光学院中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#文章題#売買損益と食塩水#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#聖光学院中学
指導講師:
重吉
問題文全文(内容文):
(1) 次の計算の□にあてはまる数を答えなさい。
\[
\left\{ (2.2 - \Box) \times 1.75 + 0.7 \right\} \div 1.625 = 0.8
\]
(2) 濃度が5%の食塩水が600gあります。この食塩水に、食塩、水、5%の食塩水を □gずつ加えたところ、濃度は10%になりました。このとき、 □にあてはまる数を答えなさい。
(3) 昨年,日本では新紙幣が発行されました。ある店舗の自動券売機の中にある。
千円札,五千円札、一万円札の枚数を調べたところ、以下のようになりました。
・紙幣の総枚数は37枚
・新五千円札と旧五千円札の枚数の比は1:3
・新一万円札は旧一万円札より2枚多い
・千円札は新旧あわせて17枚
・新一万円札と新五千円札の枚数の和と、新千円札の枚数は同じ
・旧五千円札と旧千円札の総額は、新五千円札と新千円札の総額の2倍
このとき、新五千円札は ア 枚、旧一万円札は イ枚です。 アとイにあてはまる数を答えなさい。
この動画を見る
(1) 次の計算の□にあてはまる数を答えなさい。
\[
\left\{ (2.2 - \Box) \times 1.75 + 0.7 \right\} \div 1.625 = 0.8
\]
(2) 濃度が5%の食塩水が600gあります。この食塩水に、食塩、水、5%の食塩水を □gずつ加えたところ、濃度は10%になりました。このとき、 □にあてはまる数を答えなさい。
(3) 昨年,日本では新紙幣が発行されました。ある店舗の自動券売機の中にある。
千円札,五千円札、一万円札の枚数を調べたところ、以下のようになりました。
・紙幣の総枚数は37枚
・新五千円札と旧五千円札の枚数の比は1:3
・新一万円札は旧一万円札より2枚多い
・千円札は新旧あわせて17枚
・新一万円札と新五千円札の枚数の和と、新千円札の枚数は同じ
・旧五千円札と旧千円札の総額は、新五千円札と新千円札の総額の2倍
このとき、新五千円札は ア 枚、旧一万円札は イ枚です。 アとイにあてはまる数を答えなさい。
2025年海城中入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#海城中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1)動画内参照
(2) 学校の廊下の幅を、まっすぐな2本の棒AとBを用いて測ります。棒Aで測ると5本と6/7本分、棒Bで測ると6本と5/6本分でした。棒AとBの長さの差が6cmのとき、廊下の幅は何cmですか。
(3) 原価300円の商品を150個仕入れました。はじめ2割の利益を見こんで定価をつけて販売しましたがいくつか売れ残りました。そこで、定価の2割引きで販売したところすべて売り切れ、全体で5328円の利益がありました。定価で売った 個数を求めなさい。
(4) 分母が60である分数のうち、0より大きく1より小さいものを考えます。
1/60,2/60,3/60,4/60,5/60,....,58/60,59/60
この中で約分できない分数は何個ありますか。
(5) 図の円上の点は円を9等分した点です。このとき、角アの大きさを求めなさい。
※図は動画内参照
この動画を見る
大問1
(1)動画内参照
(2) 学校の廊下の幅を、まっすぐな2本の棒AとBを用いて測ります。棒Aで測ると5本と6/7本分、棒Bで測ると6本と5/6本分でした。棒AとBの長さの差が6cmのとき、廊下の幅は何cmですか。
(3) 原価300円の商品を150個仕入れました。はじめ2割の利益を見こんで定価をつけて販売しましたがいくつか売れ残りました。そこで、定価の2割引きで販売したところすべて売り切れ、全体で5328円の利益がありました。定価で売った 個数を求めなさい。
(4) 分母が60である分数のうち、0より大きく1より小さいものを考えます。
1/60,2/60,3/60,4/60,5/60,....,58/60,59/60
この中で約分できない分数は何個ありますか。
(5) 図の円上の点は円を9等分した点です。このとき、角アの大きさを求めなさい。
※図は動画内参照
2025年雙葉中入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#雙葉中学
指導講師:
重吉
問題文全文(内容文):
[ 1] ア ~キにあてはまる数を書きましょう。(式と計算と答え)
(2) 右の図は半円を組み合わせたものです。3つの半円の中心は同じで、半径の比は、1:2:3です。
1番大きい円の半径が9cmのとき、かげをつけた部分の周りの長さは合計で イ cmです。
※図は動画内参照
(3) 日本で使われる部屋の広さを表す単位として「帖」があります。1帖は、 そうじ 1.62 m²です。掃除ロボットAは、6帖を掃除するのに27分かかり、 掃除ロボットBは、10帖を掃除するのに30分かかります。2つのロボットA、B が同時に 37.44m² の部屋を掃除するのに ウ分 エ秒かかります。
(4)下の表は、40人の生徒が50点満点のテストを受けた結果を表したものです。
※図は動画内参照
中央値が35点、最頻値が40点、平均値はキ点でした。
この動画を見る
[ 1] ア ~キにあてはまる数を書きましょう。(式と計算と答え)
(2) 右の図は半円を組み合わせたものです。3つの半円の中心は同じで、半径の比は、1:2:3です。
1番大きい円の半径が9cmのとき、かげをつけた部分の周りの長さは合計で イ cmです。
※図は動画内参照
(3) 日本で使われる部屋の広さを表す単位として「帖」があります。1帖は、 そうじ 1.62 m²です。掃除ロボットAは、6帖を掃除するのに27分かかり、 掃除ロボットBは、10帖を掃除するのに30分かかります。2つのロボットA、B が同時に 37.44m² の部屋を掃除するのに ウ分 エ秒かかります。
(4)下の表は、40人の生徒が50点満点のテストを受けた結果を表したものです。
※図は動画内参照
中央値が35点、最頻値が40点、平均値はキ点でした。
2025年武蔵中入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#武蔵中学
指導講師:
重吉
問題文全文(内容文):
大問1
次の▭ にあてはまる数を書き入れなさい。
(1)
(ア) 3%の食塩水▭ gに、5.5%の食塩水を加えて120gの食塩水を作ったところ、
できた食塩水は4%になりました。
(イ) %の食塩水が80g入っている容器に、3.5%の食塩水を160g加えた
ところ、容器の中の食塩水の濃度は1/2倍になりました。
(2) 200枚のコインがすべて表向きに横一列に並べてあります。最初に、左から偶数番目のコインをすべてひっくり返します。次に、左から3の倍数番目(3番目,6番目, 9番日……)のコインをすべてひっくり返します。このとき、表向きになっているコインは全部で▭枚です。さらに、左から5の倍数番目(5番日,10番日, 15番目……)のコインをすべてひっくり返すと、表向きになっているコインは全部で▭枚です。
この動画を見る
大問1
次の▭ にあてはまる数を書き入れなさい。
(1)
(ア) 3%の食塩水▭ gに、5.5%の食塩水を加えて120gの食塩水を作ったところ、
できた食塩水は4%になりました。
(イ) %の食塩水が80g入っている容器に、3.5%の食塩水を160g加えた
ところ、容器の中の食塩水の濃度は1/2倍になりました。
(2) 200枚のコインがすべて表向きに横一列に並べてあります。最初に、左から偶数番目のコインをすべてひっくり返します。次に、左から3の倍数番目(3番目,6番目, 9番日……)のコインをすべてひっくり返します。このとき、表向きになっているコインは全部で▭枚です。さらに、左から5の倍数番目(5番日,10番日, 15番目……)のコインをすべてひっくり返すと、表向きになっているコインは全部で▭枚です。
2025年筑波大学附属駒場中入試問題算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#筑波大学附属駒場中学#筑波大学附属中学
指導講師:
重吉
問題文全文(内容文):
[1] 1から9までの整数のうち、いずれか1つが
書かれたカードがあります。
これらのカードを、右の図のようにならんだア~ケのマス目に1枚ずつ置くことを考えます。
ただし、
アには 123 の3枚のカードから1枚を
イウエには 445566の6枚のカードから3枚を
オカキクケには 777888999 の9枚のカードから5枚を
それぞれ選んで置くものとします。
ここでは、たとえばアのマス目に置いたカードのことを、アのカードということにします。 次の問いに答えなさい。
(1)ア、ウ、キのカードに書かれた3つの数について考えます。
ア、ウ、キのカードに書かれた3つの数の合計が、3の倍数となりました。
このような3枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。
(2)ア、イ、ウ、エ、キのカードに書かれた5つの数について考えます。
ア、ウ、キのカードに書かれた3つの数の合計と、
イ、ウ、エのカードに書かれた3つの数の合計が、どちらも3の倍数となりました。
このような5枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。
(3) ア~ケのカードに書かれた9つの数について考えます。
ア、ウ 、キのカードに書かれた3つの数の合計、
イ、ウ、エのカードに書かれた3つの数の合計、
オ、カ、キ、ク、ケのカードに書かれた5つの数の合計が、すべて3の倍数となりました。
このような9枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。
この動画を見る
[1] 1から9までの整数のうち、いずれか1つが
書かれたカードがあります。
これらのカードを、右の図のようにならんだア~ケのマス目に1枚ずつ置くことを考えます。
ただし、
アには 123 の3枚のカードから1枚を
イウエには 445566の6枚のカードから3枚を
オカキクケには 777888999 の9枚のカードから5枚を
それぞれ選んで置くものとします。
ここでは、たとえばアのマス目に置いたカードのことを、アのカードということにします。 次の問いに答えなさい。
(1)ア、ウ、キのカードに書かれた3つの数について考えます。
ア、ウ、キのカードに書かれた3つの数の合計が、3の倍数となりました。
このような3枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。
(2)ア、イ、ウ、エ、キのカードに書かれた5つの数について考えます。
ア、ウ、キのカードに書かれた3つの数の合計と、
イ、ウ、エのカードに書かれた3つの数の合計が、どちらも3の倍数となりました。
このような5枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。
(3) ア~ケのカードに書かれた9つの数について考えます。
ア、ウ 、キのカードに書かれた3つの数の合計、
イ、ウ、エのカードに書かれた3つの数の合計、
オ、カ、キ、ク、ケのカードに書かれた5つの数の合計が、すべて3の倍数となりました。
このような9枚のカードの置き方として、考えられるものは全部で何通りありますか。
ただし、同じ数が書かれたカードどうしは区別しないものとします。
2025年早稲田実業中入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#早稲田実業中等部
指導講師:
重吉
問題文全文(内容文):
大問1
(2)2桁の整数A、Bがあります。AとBの最大公約数は6、最小公倍数は360です。AはBより大きいとき、Aにあてはまる数をすべて求めなさい。
(3) 500円硬貨,100円硬貨,50円硬貨がたくさんあります。これらの硬貨を使って1600円を支払う
方法は何通りありますか。ただし、使わない硬貨があってもよいものとします。
(4) ある学校の入学試験の合格者は受験者全体の40%で、合格者の平均点は合格最低点より12点高く、不合格者の平均点は合格最低点より13点低かったです。また、受験者全体の平均点は60点でした。このとき、合格最低点を求めなさい。
この動画を見る
大問1
(2)2桁の整数A、Bがあります。AとBの最大公約数は6、最小公倍数は360です。AはBより大きいとき、Aにあてはまる数をすべて求めなさい。
(3) 500円硬貨,100円硬貨,50円硬貨がたくさんあります。これらの硬貨を使って1600円を支払う
方法は何通りありますか。ただし、使わない硬貨があってもよいものとします。
(4) ある学校の入学試験の合格者は受験者全体の40%で、合格者の平均点は合格最低点より12点高く、不合格者の平均点は合格最低点より13点低かったです。また、受験者全体の平均点は60点でした。このとき、合格最低点を求めなさい。
2025年慶應義塾中等部入試算数大問① 中学受験指導歴20年以上プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
【1】 次の□に適当な数を入れなさい。
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right) = \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(2)
\[
\left\{ 3.88 - \frac{2}{3} \times \left( 2\frac{1}{6} + 3\frac{1}{3} \right) \right\} \div \left( 5\frac{1}{2} - \frac{\boxed{\text{イ}}}{\boxed{\text{ア}}} \right) = \frac{8}{175}
\]
(3)
\[
\frac{3}{7} で割っても\, 2\frac{4}{5} をかけても整数になる数のうち、最も小さい数は\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(4) 1, 2, 3, 4,5の5個の数字の中から、異なる3個の数字を選んで3桁の整数をつくるとき、250以上450未満の整数は全部で□個つくることができます。
(5) 2025の約数をすべて加えると□になります。
この動画を見る
【1】 次の□に適当な数を入れなさい。
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right) = \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(2)
\[
\left\{ 3.88 - \frac{2}{3} \times \left( 2\frac{1}{6} + 3\frac{1}{3} \right) \right\} \div \left( 5\frac{1}{2} - \frac{\boxed{\text{イ}}}{\boxed{\text{ア}}} \right) = \frac{8}{175}
\]
(3)
\[
\frac{3}{7} で割っても\, 2\frac{4}{5} をかけても整数になる数のうち、最も小さい数は\quad \boxed{\text{ア}}\frac{\boxed{\text{イ}}}{\boxed{\text{ウ}}}
\]
(4) 1, 2, 3, 4,5の5個の数字の中から、異なる3個の数字を選んで3桁の整数をつくるとき、250以上450未満の整数は全部で□個つくることができます。
(5) 2025の約数をすべて加えると□になります。
2025年早稲田中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#文章題その他#早稲田中学
指導講師:
重吉
問題文全文(内容文):
(1) 次のように、ある規則にしたがって数が並んでいます。並べられた数の和を答えなさい。
1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 7, 8, 7, 8, 9, 10,.....75, 76, 77, 78, 77, 78, 79, 80
(2) バス停からバス停Bまで5kmあり、途中に体育館があります。バス停 A もどから体育館まで行くのに、自転車で行く場合と、バスに乗ってバス停Bまで行き、体育館まで歩いて戻る場合では同じ時間かかります。バスは分速800m,自転車は分速180mで進み、歩く速さは分速45mです。バス停Aから体育館までの道のりは何mですか。
(3) みかん、りんご、ももの1個あたりの値段はそれぞれ100円,150円,173円 。これらの果物を3403円分おつりがないように買います。個数の合計が最も多くなるように買うには、みかん、りんご、ももをそれぞれ何個ずつ買えばよいですか。ただし、どの果物も1個以上は買うものとします。
この動画を見る
(1) 次のように、ある規則にしたがって数が並んでいます。並べられた数の和を答えなさい。
1, 2, 3, 4, 3, 4, 5, 6, 5, 6, 7, 8, 7, 8, 9, 10,.....75, 76, 77, 78, 77, 78, 79, 80
(2) バス停からバス停Bまで5kmあり、途中に体育館があります。バス停 A もどから体育館まで行くのに、自転車で行く場合と、バスに乗ってバス停Bまで行き、体育館まで歩いて戻る場合では同じ時間かかります。バスは分速800m,自転車は分速180mで進み、歩く速さは分速45mです。バス停Aから体育館までの道のりは何mですか。
(3) みかん、りんご、ももの1個あたりの値段はそれぞれ100円,150円,173円 。これらの果物を3403円分おつりがないように買います。個数の合計が最も多くなるように買うには、みかん、りんご、ももをそれぞれ何個ずつ買えばよいですか。ただし、どの果物も1個以上は買うものとします。
2025年豊島岡女子学園中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
この動画を見る
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
2つの二次方程式 2025立教新座

単元:
#算数(中学受験)#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式#過去問解説(学校別)#立教新座中学
指導講師:
数学を数楽に
問題文全文(内容文):
2つの2次方程式
$x^2-kx-10=0$
$x^2+5x+2k=0$
が共通解を1つだけ持つ。この共有解と定数$k$の値を求めよ。
ただし$k≠5$
この動画を見る
2つの2次方程式
$x^2-kx-10=0$
$x^2+5x+2k=0$
が共通解を1つだけ持つ。この共有解と定数$k$の値を求めよ。
ただし$k≠5$
2025年渋谷教育学園渋谷中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#平面図形その他#速さ#速さその他#場合の数#場合の数#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
(1) \[
\frac{1}{2} + 7.15 \div \left( \frac{5}{7} - 1.875 \times \frac{2}{15} \right)
\]
(2) 渋男さんと教子さんは、駅から学校までジョギングをしました。駅と学校のちょうど真ん中に公園があります。2人は駅を同時に出発し、学校に同時に着きました。渋男さんは駅から公園までは時速8km、公園から学校までは時速12kmで走りました。救子さんは駅から学校まで一定の速さで走りました。教子さんの速さは時速何kmですか。
(3) 【A】はAの約数の個数を表します。例えば、6の約数は1.2.3.6なので 【6】=4です。
このとき、【【2025】×30】はいくつですか。
(4) A, B, C, D, E, F, G, H, I, J, Kの11人の生徒を5人部屋と6人部屋に分けます。 A, B, Cの3人の生徒が同じ部屋に入るとすると、11人の分け方は何通りありますか。
(5) 渋男さんと教子さんがある仕事をします。2人で一緒に行えば2時間で終わります。 同じ仕事を教子さんが1人で行うと、4時間30分で終わります。
ある日、同じ仕事を渋男さんと教子さんは9時から2人で一緒に始めました。9時40分に渋男さんは忘れ物に気づいて家へ帰りました。渋男さんがいない間、教子さんは1人で仕事をしました。渋男さんが戻ってきた後、渋男さんは1.2倍のスピードで、教子さんはこれまでと同じスピードで一緒に仕事を進めました。その結果、11時46分に終わりました。渋男さんが戻ってきたのは何時何分ですか。
(6) 下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何cmですか。
※図は動画内参照
この動画を見る
(1) \[
\frac{1}{2} + 7.15 \div \left( \frac{5}{7} - 1.875 \times \frac{2}{15} \right)
\]
(2) 渋男さんと教子さんは、駅から学校までジョギングをしました。駅と学校のちょうど真ん中に公園があります。2人は駅を同時に出発し、学校に同時に着きました。渋男さんは駅から公園までは時速8km、公園から学校までは時速12kmで走りました。救子さんは駅から学校まで一定の速さで走りました。教子さんの速さは時速何kmですか。
(3) 【A】はAの約数の個数を表します。例えば、6の約数は1.2.3.6なので 【6】=4です。
このとき、【【2025】×30】はいくつですか。
(4) A, B, C, D, E, F, G, H, I, J, Kの11人の生徒を5人部屋と6人部屋に分けます。 A, B, Cの3人の生徒が同じ部屋に入るとすると、11人の分け方は何通りありますか。
(5) 渋男さんと教子さんがある仕事をします。2人で一緒に行えば2時間で終わります。 同じ仕事を教子さんが1人で行うと、4時間30分で終わります。
ある日、同じ仕事を渋男さんと教子さんは9時から2人で一緒に始めました。9時40分に渋男さんは忘れ物に気づいて家へ帰りました。渋男さんがいない間、教子さんは1人で仕事をしました。渋男さんが戻ってきた後、渋男さんは1.2倍のスピードで、教子さんはこれまでと同じスピードで一緒に仕事を進めました。その結果、11時46分に終わりました。渋男さんが戻ってきたのは何時何分ですか。
(6) 下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何cmですか。
※図は動画内参照
基本セオリーがぎゅーと詰まった良問!あの形が見えるかな?【中学受験算数】【2025年】【西京中】

2025年麻布中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#麻布中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1) 1辺の長さが1cmの正三角形Aを、1辺の長さが3cmの正三角形Bにそってすべらないように転がします。図1の位置から矢印の向きに転がしていったところ、AはBの周りを1周してもとの位置にもどりました。点Pの描いた曲線の長さを求めなさい。
※図は動画内参照
この動画を見る
大問1
(1) 1辺の長さが1cmの正三角形Aを、1辺の長さが3cmの正三角形Bにそってすべらないように転がします。図1の位置から矢印の向きに転がしていったところ、AはBの周りを1周してもとの位置にもどりました。点Pの描いた曲線の長さを求めなさい。
※図は動画内参照
2025年桜蔭中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#桜蔭中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1)
\[
\left( \frac{15}{7} + 0.6 \right) \times \boxed{\text{ア}} + 6 \frac{7}{13} - \frac{19}{91} = 9
\]
(2) 底面が正方形の直方体Pと、円柱Qがあります。2つの立体の高さは同じです。図のように、 直方体Pには底面のAからBへ、円柱Qには底面のCからDへ、長さが最も短くなるように側面を1周させて糸を巻きつけたところ、2つの立体に巻きつけた糸の長さは同じとなりました。
① 直方体Pの底面の1辺の長さは、円柱Qの底面の半径の$\boxed{\text{イ}}$倍です。
② 直方体Pの体積は、円柱の体積の$\boxed{\text{ウ}}$倍です。
※図は動画内参照
(3) ある整数nを4で割った余りを(n),7で割った余りを [n] と表すことにします。
たとえば、 6÷4 = 1 余り2なので(6)=2
6÷7 = 0 余り6なので [6] =6 です。
① (n)= 3 である1以上の整数nについて考えます。
小さい順に並べたとき、2025番目に来る数は$\boxed{\text{エ}}$です。また、1番目から2025番目までの数のうち、 [n] = 5 となる数は $\boxed{\text{オ}}$個あります。
② 1から100までの整数のうち、 (n)= [n] となる整数は $\boxed{\text{カ}}$個あります。
この動画を見る
大問1
(1)
\[
\left( \frac{15}{7} + 0.6 \right) \times \boxed{\text{ア}} + 6 \frac{7}{13} - \frac{19}{91} = 9
\]
(2) 底面が正方形の直方体Pと、円柱Qがあります。2つの立体の高さは同じです。図のように、 直方体Pには底面のAからBへ、円柱Qには底面のCからDへ、長さが最も短くなるように側面を1周させて糸を巻きつけたところ、2つの立体に巻きつけた糸の長さは同じとなりました。
① 直方体Pの底面の1辺の長さは、円柱Qの底面の半径の$\boxed{\text{イ}}$倍です。
② 直方体Pの体積は、円柱の体積の$\boxed{\text{ウ}}$倍です。
※図は動画内参照
(3) ある整数nを4で割った余りを(n),7で割った余りを [n] と表すことにします。
たとえば、 6÷4 = 1 余り2なので(6)=2
6÷7 = 0 余り6なので [6] =6 です。
① (n)= 3 である1以上の整数nについて考えます。
小さい順に並べたとき、2025番目に来る数は$\boxed{\text{エ}}$です。また、1番目から2025番目までの数のうち、 [n] = 5 となる数は $\boxed{\text{オ}}$個あります。
② 1から100までの整数のうち、 (n)= [n] となる整数は $\boxed{\text{カ}}$個あります。
式の値 昭和学院秀英
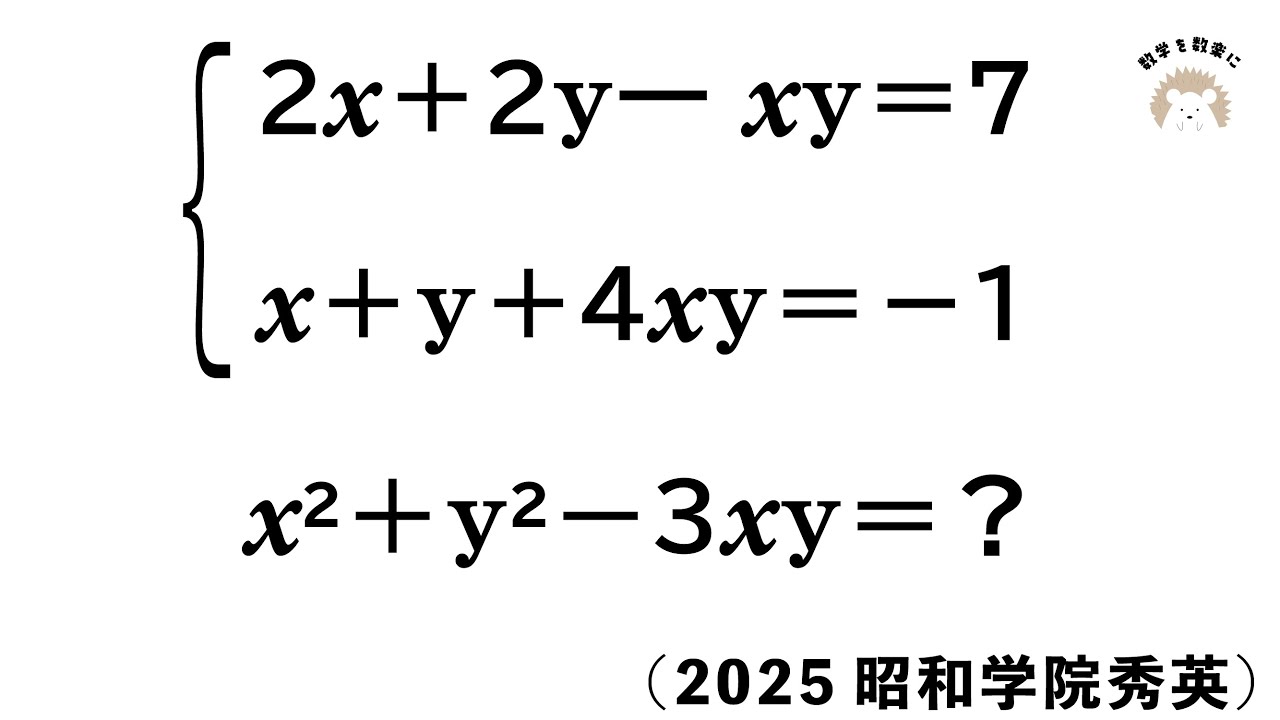
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#昭和学院秀英中学
指導講師:
数学を数楽に
問題文全文(内容文):
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
この動画を見る
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
2025年開成中入試問題算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#開成中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1) (0.02km + 13m - 40cm)(2.3m + 32cm - 120mm) は何aですか。
(2) ショウヘイ君はいくらかのお金を所持しています。まず、所持金の $\frac{1}{9}$より20円安い商品Aを買いました。次に、残金の$\frac{1}{7}$より40円安い商品Bを買いました。続けて、このときの残金の$\frac{1}{5}$より10円安い商品Cを買ったところ、最後に残ったお金ははじめの所持金の4割より480円多かったそうです。商品の値段はいくらでしたか。
この動画を見る
大問1
(1) (0.02km + 13m - 40cm)(2.3m + 32cm - 120mm) は何aですか。
(2) ショウヘイ君はいくらかのお金を所持しています。まず、所持金の $\frac{1}{9}$より20円安い商品Aを買いました。次に、残金の$\frac{1}{7}$より40円安い商品Bを買いました。続けて、このときの残金の$\frac{1}{5}$より10円安い商品Cを買ったところ、最後に残ったお金ははじめの所持金の4割より480円多かったそうです。商品の値段はいくらでしたか。
2025年渋谷教育学園幕張中入試算数大問② 中学受験指導歴20年以上プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#渋谷教育学園渋谷中学#渋谷教育学園幕張中学校
指導講師:
重吉
問題文全文(内容文):
大問2
2つの数A.Bは、3.4.5.6.8.9のいずれかの数であり、異なるものとします。
4けたの数 A77Bをアとします。アの各位の数を、左から小さい順に並べかえて作った4けたの数をイとします。アからイを引いた数をウとします。例えば、 A = 6 、B = 5 とすると、ア=6775、イ=5677であり、ウ=1098 です。
次の各問いに答えなさい。
(1)ウとして考えられる最も大きな数を答えなさい。
(2)ウが2けたの数になるAとBの組は何通りありますか。
(3)ウが3けたの数になるAとBの組は何通りありますか。
この動画を見る
大問2
2つの数A.Bは、3.4.5.6.8.9のいずれかの数であり、異なるものとします。
4けたの数 A77Bをアとします。アの各位の数を、左から小さい順に並べかえて作った4けたの数をイとします。アからイを引いた数をウとします。例えば、 A = 6 、B = 5 とすると、ア=6775、イ=5677であり、ウ=1098 です。
次の各問いに答えなさい。
(1)ウとして考えられる最も大きな数を答えなさい。
(2)ウが2けたの数になるAとBの組は何通りありますか。
(3)ウが3けたの数になるAとBの組は何通りありますか。
重吉の母校久留米附設中2025年入試算数大問① 中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#久留米大学附設中学
指導講師:
重吉
問題文全文(内容文):
(1)
\[
(16 \times 16 - \Box) \div \left(17 \div 1000 + 27 \div 250\right) = 2000
\]
(2) 2,3,4の3つの数の中から1つを選んで0に足していく操作を繰り返します。足した数の合計がちょうど8になって操作を終了したとき、次の①、②の場合、数の足し方はそれぞれ何通りありますか。
①足した数の順番が異なるものも同じものとして数える場合
②足した数の順番が異なるものは別のものとして数える場合
(3)図のように、正五角形と正八角形が1辺を共有して重なっています。
アの角度は何度ですか。小数で答えなさい。
※図は動画内参照
(4) 図のように、1辺の長さが6cmの立方体ABCD-EFGHがあり、正方形ABCDの対角線の交点をOとします。四角すいO-EFGH を立体Xとし、Xを4点A,F,GDを通る平面Yで切断するとき、OHと平面Yの交点をPとします。
①比OP:PHを最も簡単な整数比で答えなさい。
②点Oを含むほうの立体の体積は何㎤ですか。
※図は動画内参照
この動画を見る
(1)
\[
(16 \times 16 - \Box) \div \left(17 \div 1000 + 27 \div 250\right) = 2000
\]
(2) 2,3,4の3つの数の中から1つを選んで0に足していく操作を繰り返します。足した数の合計がちょうど8になって操作を終了したとき、次の①、②の場合、数の足し方はそれぞれ何通りありますか。
①足した数の順番が異なるものも同じものとして数える場合
②足した数の順番が異なるものは別のものとして数える場合
(3)図のように、正五角形と正八角形が1辺を共有して重なっています。
アの角度は何度ですか。小数で答えなさい。
※図は動画内参照
(4) 図のように、1辺の長さが6cmの立方体ABCD-EFGHがあり、正方形ABCDの対角線の交点をOとします。四角すいO-EFGH を立体Xとし、Xを4点A,F,GDを通る平面Yで切断するとき、OHと平面Yの交点をPとします。
①比OP:PHを最も簡単な整数比で答えなさい。
②点Oを含むほうの立体の体積は何㎤ですか。
※図は動画内参照
2025年灘中1日目入試算数大問⑦、⑧ 中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#灘中学校
指導講師:
重吉
問題文全文(内容文):
大問7
8個の数3,4,5,6,7,8,9,0を並べ替えると、 A, B, C, D, E, F, G, Hとなりました。
5桁の整数 1ABC2をDで割ると割り切れ、商が4桁の整数 EFGH となるとき、整数 EFGH は▭です。
大問8
図のように、平行四辺形ABCDがあり、点E, F は辺BCを3等分し、点G, H, Iは辺ADを4等分しています。3直線BD, EI, FGで囲まれた斜線部分の面積は平行四辺形ABCDの面積の▭倍です。
※図は動画内参照
この動画を見る
大問7
8個の数3,4,5,6,7,8,9,0を並べ替えると、 A, B, C, D, E, F, G, Hとなりました。
5桁の整数 1ABC2をDで割ると割り切れ、商が4桁の整数 EFGH となるとき、整数 EFGH は▭です。
大問8
図のように、平行四辺形ABCDがあり、点E, F は辺BCを3等分し、点G, H, Iは辺ADを4等分しています。3直線BD, EI, FGで囲まれた斜線部分の面積は平行四辺形ABCDの面積の▭倍です。
※図は動画内参照
2025年灘中1日目算数入試大問④~⑥中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師:
重吉
問題文全文(内容文):
4,
2025は9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0です。4桁の整数のよくうち、9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0であるものは2025を含
めて全部で▭個あります。
5,
A駅ではB駅行き、C駅行き、D駅行きの3種類の電車が、それぞれ一定の間隔で発車します。 ある日、3種類の最初の電車が同時に発車し、3種類の最後の電車も同時に発車し、B駅行きは69本 C駅行きは71本、D駅行きは41本発車しました。この日、3種類の電車が同時に発車したのは最初と最後を含めて全部で ① 回で、3種類のうち2種類の電車のみが同時に発車したのは全部で② 回でした。
6,
右の図(動画内参照)は、1×1から9×9の81個の数を表にしたものです。太線の長方形の中に書かれたすべての数のけいせん和は315です。この表の罫線で囲まれた長方形は全部で 2025個ありますが、そのうち、中に書かれたすべての数の和が315であるものは、太線の長方形を含めて全部個あります。ただし、正方形は長方形にで含まれるとします。
この動画を見る
4,
2025は9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0です。4桁の整数のよくうち、9の倍数でも25の倍数でもあり、4つの位の数のうち1つだけが0であるものは2025を含
めて全部で▭個あります。
5,
A駅ではB駅行き、C駅行き、D駅行きの3種類の電車が、それぞれ一定の間隔で発車します。 ある日、3種類の最初の電車が同時に発車し、3種類の最後の電車も同時に発車し、B駅行きは69本 C駅行きは71本、D駅行きは41本発車しました。この日、3種類の電車が同時に発車したのは最初と最後を含めて全部で ① 回で、3種類のうち2種類の電車のみが同時に発車したのは全部で② 回でした。
6,
右の図(動画内参照)は、1×1から9×9の81個の数を表にしたものです。太線の長方形の中に書かれたすべての数のけいせん和は315です。この表の罫線で囲まれた長方形は全部で 2025個ありますが、そのうち、中に書かれたすべての数の和が315であるものは、太線の長方形を含めて全部個あります。ただし、正方形は長方形にで含まれるとします。
【受験算数】平面図形:合同な図形を探す 【洛南高附中2019】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#洛南高校附属中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
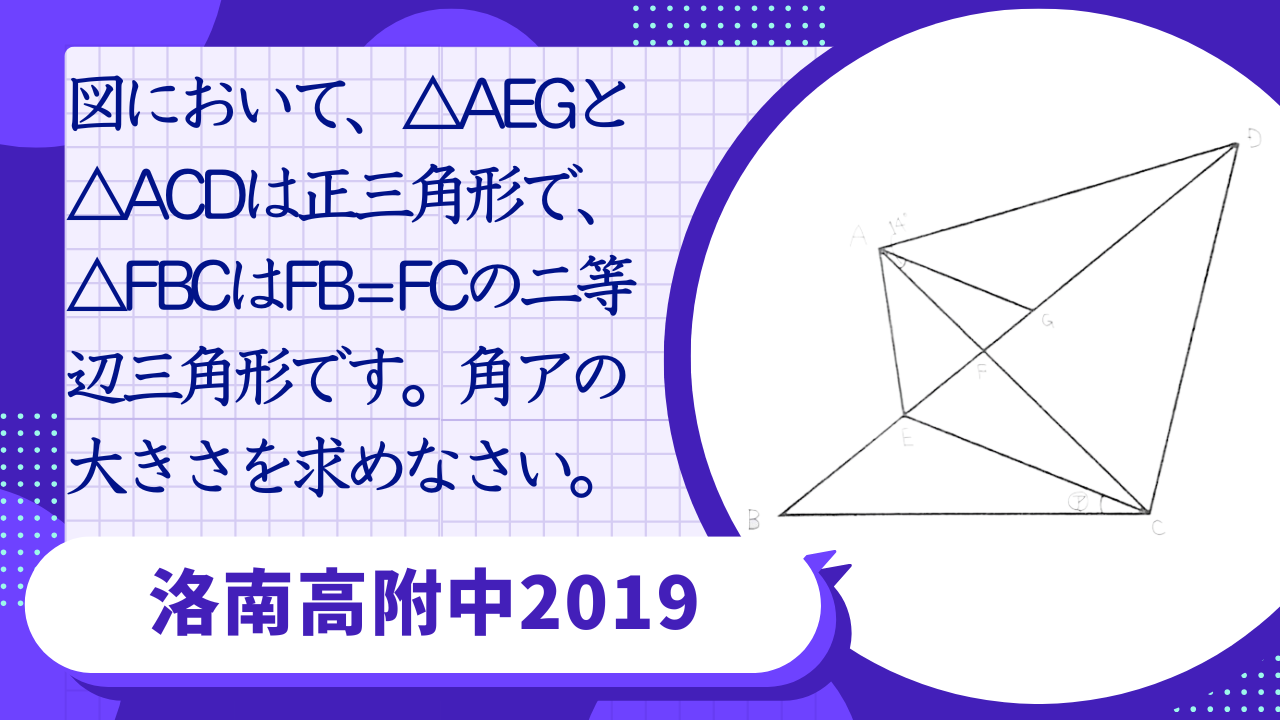
図において、△AEGと△ACDは正三角形で、△FBCはFB=FCの二等辺三角形です。角アの大きさを求めなさい。
この動画を見る
図において、△AEGと△ACDは正三角形で、△FBCはFB=FCの二等辺三角形です。角アの大きさを求めなさい。
