 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
【中学受験算数】【最終回】ゼロから始める中学受験算数50 最終回!容器に水を入れる問題!!
単元:
#算数(中学受験)#単位・比と割合・比例・反比例#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
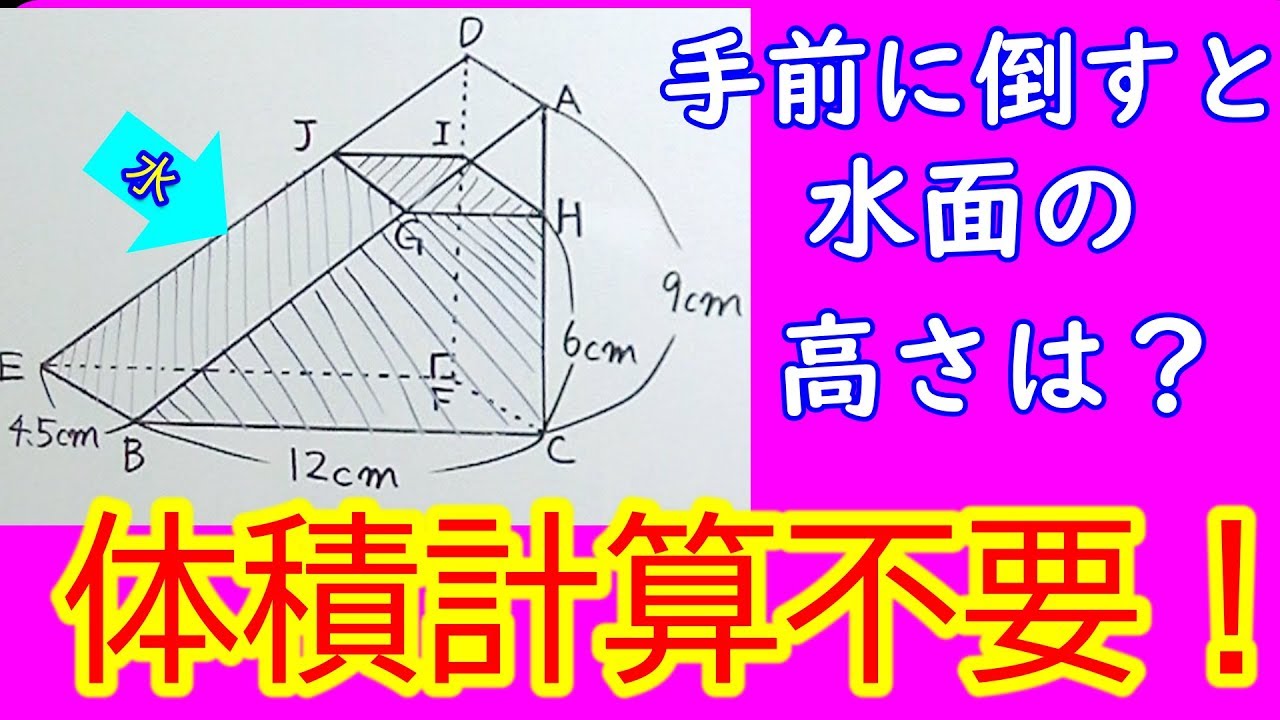
1⃣下の図のような三角柱の容器の中に、深さ半分のところまで水が入っています。この容器を、三角形ABCの部分が底になるように置くと、水の深さは何㎝になりますか。
2⃣図1のような水そうに、一定の割合で水を入れました。図2のグラフは水を入れ始めてからの時間と、アの部分の水の深さの関係を表したものです。
(1)1分間に何㎤の水を入れましたか。
(2)図1のxを求めましょう。
3⃣下の図のような形をした水そうに、一定の割合で水を入れたところ、5分30秒でいっぱいになりました。グラフは水をいれはじめてからの時間と水の深さとの関係を表したものです。
(1)1分間に何㎤の水を入れたか。
(2)xの値を求めましょう。
(3)最も深い部分は何㎝ですか。
*図は動画内参照
この動画を見る
1⃣下の図のような三角柱の容器の中に、深さ半分のところまで水が入っています。この容器を、三角形ABCの部分が底になるように置くと、水の深さは何㎝になりますか。
2⃣図1のような水そうに、一定の割合で水を入れました。図2のグラフは水を入れ始めてからの時間と、アの部分の水の深さの関係を表したものです。
(1)1分間に何㎤の水を入れましたか。
(2)図1のxを求めましょう。
3⃣下の図のような形をした水そうに、一定の割合で水を入れたところ、5分30秒でいっぱいになりました。グラフは水をいれはじめてからの時間と水の深さとの関係を表したものです。
(1)1分間に何㎤の水を入れたか。
(2)xの値を求めましょう。
(3)最も深い部分は何㎝ですか。
*図は動画内参照
【中学受験算数】【立体】ゼロから始める中学受験算数49 立体図形問題にセンスは必要ない!誰でも解ける方法を教えます!!
単元:
#算数(中学受験)#立体図形#立体図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
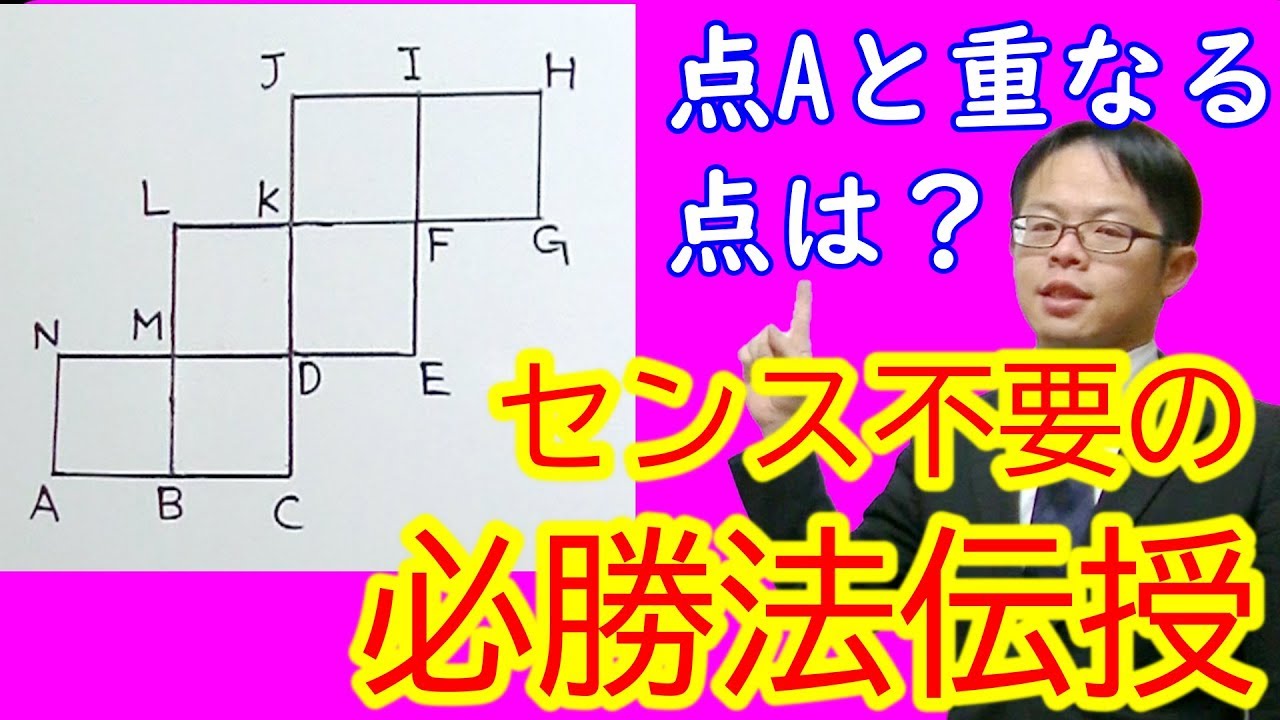
1⃣下の図は立方体の展開図です。この展開図を組み立てます。
(1)点Aと重なる点をすべて答えましょう。
(2)辺FGと重なる辺を答えましょう。
2⃣同じ大きさの立方体の積み木を使って、ある立体をつくりました。
下の図は、この立体を真正面から見た図と真上から見た図です。
(1)使っている積み木の数は最も多くて何個ですか。
(2)使っている積み木の数は最も少なくて何個ですか。
*図は動画内参照
この動画を見る
1⃣下の図は立方体の展開図です。この展開図を組み立てます。
(1)点Aと重なる点をすべて答えましょう。
(2)辺FGと重なる辺を答えましょう。
2⃣同じ大きさの立方体の積み木を使って、ある立体をつくりました。
下の図は、この立体を真正面から見た図と真上から見た図です。
(1)使っている積み木の数は最も多くて何個ですか。
(2)使っている積み木の数は最も少なくて何個ですか。
*図は動画内参照
【中学受験算数】【回転体】ゼロから始める中学受験算数48 センスが無くても解ける!回転体の体積!切断された直方体の体積!

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図の台形ABCDを、辺DCを軸として1回転させてできる立体の体積を求めましょう。
2⃣下の図は直方体をななめに切断してできた立体です。
この立体の体積は何㎤ですか。
*図は動画内参照
この動画を見る
1⃣下の図の台形ABCDを、辺DCを軸として1回転させてできる立体の体積を求めましょう。
2⃣下の図は直方体をななめに切断してできた立体です。
この立体の体積は何㎤ですか。
*図は動画内参照
【中学受験算数】【円すい】【裏技】ゼロから始める中学受験算数47 裏技公式で一発解決!!円柱・円錐の体積・表面積!!

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図のような円柱の体積と表面積を求めましょう。
2⃣下の図のような円すいの体積と表面積を求めましょう。
*図は動画内参照
この動画を見る
1⃣下の図のような円柱の体積と表面積を求めましょう。
2⃣下の図のような円すいの体積と表面積を求めましょう。
*図は動画内参照
【中学受験算数】【体積】【表面積】ゼロから始める中学受験算数46 スッキリ解決!直方体と立方体の体積・表面積!
単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣たて5㎝、横8㎝、高さ6㎝の直方体の体積と表面積を求めましょう。
2⃣1辺が7㎝の立方体の体積と表面積を求めましょう。
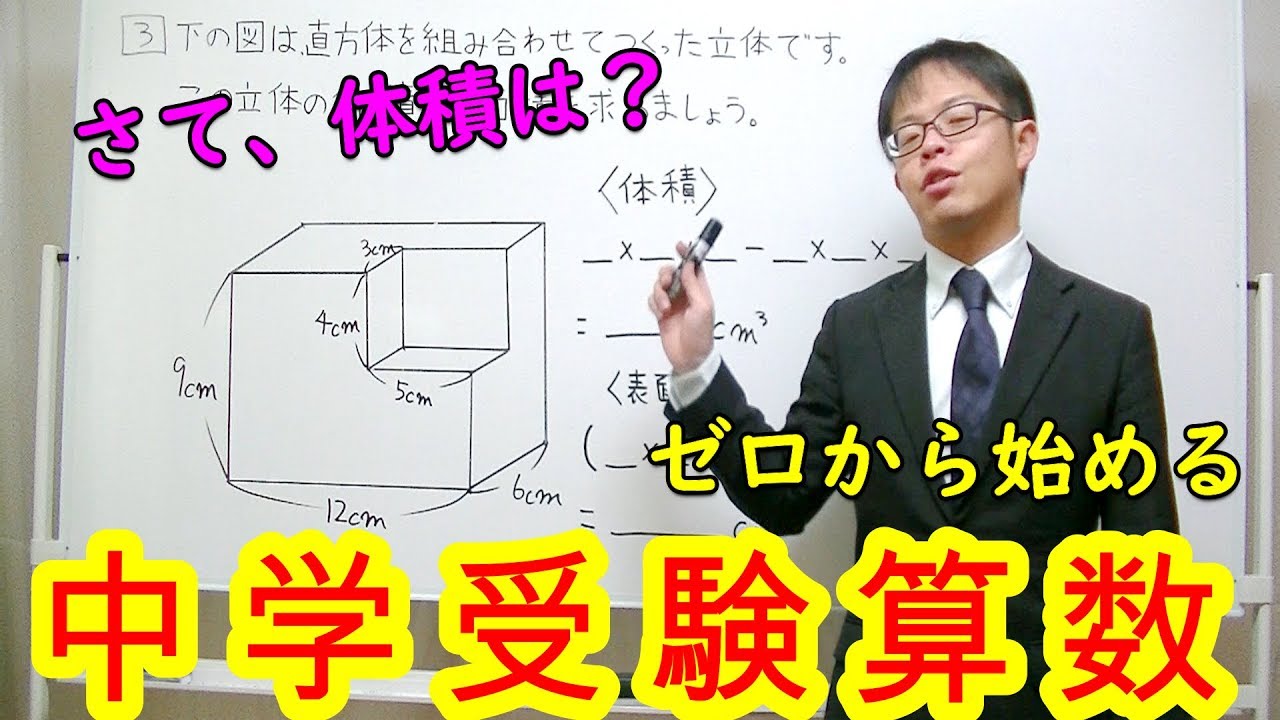
3⃣下の図は直方体を組み合わせてつくった立体です。
この立体の体積と表面積を求めましょう。
*図は動画内参照
この動画を見る
1⃣たて5㎝、横8㎝、高さ6㎝の直方体の体積と表面積を求めましょう。
2⃣1辺が7㎝の立方体の体積と表面積を求めましょう。
3⃣下の図は直方体を組み合わせてつくった立体です。
この立体の体積と表面積を求めましょう。
*図は動画内参照
【中学受験算数】【円が転がる】ゼロから始める中学受験算数45 円が転がる問題を分かりやすく解説!!

単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#速さ#点の移動・時計算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図のように、半径5㎝の円が、たて15㎝、横30㎝の長方形の辺にそって外側を1周します。このとき、円の中心がえがく線の長さと、円が通る部分の面積を求めましょう。
2⃣下の図のように、たて12㎝、横16㎝の長方形ABCDの外側と内側を半径2㎝の円P、円Qがそれぞれ辺にそって1周します。このとき、円Pと円Qの中心がえがく線の長さをそれぞれ求めましょう。
3⃣下の図のような長方形ABCDがあり、点Pは点Aを出発し、点B、Cを通って点Dまで、毎秒2㎝の速さで動きます。
(1)点Pが出発してから3秒後の三角形PADの面積を求めましょう。
(2)三角形PADの面積が変わらないのは、点Pが出発後、何秒後から何秒後までですか。
*図は動画内参照
この動画を見る
1⃣下の図のように、半径5㎝の円が、たて15㎝、横30㎝の長方形の辺にそって外側を1周します。このとき、円の中心がえがく線の長さと、円が通る部分の面積を求めましょう。
2⃣下の図のように、たて12㎝、横16㎝の長方形ABCDの外側と内側を半径2㎝の円P、円Qがそれぞれ辺にそって1周します。このとき、円Pと円Qの中心がえがく線の長さをそれぞれ求めましょう。
3⃣下の図のような長方形ABCDがあり、点Pは点Aを出発し、点B、Cを通って点Dまで、毎秒2㎝の速さで動きます。
(1)点Pが出発してから3秒後の三角形PADの面積を求めましょう。
(2)三角形PADの面積が変わらないのは、点Pが出発後、何秒後から何秒後までですか。
*図は動画内参照
【中学受験算数】【回転移動】ゼロから始める中学受験算数44 分かる!楽勝!平行移動と回転移動!!

単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#体積・表面積・回転体・水量・変化のグラフ
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)下の図は、直径12㎝の半円を真上方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(2)下の図は、半径2㎝の円を真横方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(3)下の図は、直径12㎝の半円を点Oを中心として30°回転させたものです。
斜線部分の面積を求めましょう。
(4)下の図は、半径4㎝の半円を点Oを中心として45°回転させたものです。
斜線部分の面積を求めましょう。
2⃣下の図は、三角形ABCを、点Cを中心として矢印の方向に回転させ、辺BCと辺CA’が一直線になるように三角形A’B’Cをつくったものです。このとき、斜線部の面積を求めましょう。
3⃣下の図は、AB=4㎝、BC=3㎝、CA=5㎝の三角形ABCを点Cを中心として90°回転させて、三角形A’B’Cに移したものです。
斜線部分の面積を求めましょう。
*図は動画内参照
この動画を見る
1⃣
(1)下の図は、直径12㎝の半円を真上方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(2)下の図は、半径2㎝の円を真横方向に3㎝移動させたものです。
斜線部分の面積を求めましょう。
(3)下の図は、直径12㎝の半円を点Oを中心として30°回転させたものです。
斜線部分の面積を求めましょう。
(4)下の図は、半径4㎝の半円を点Oを中心として45°回転させたものです。
斜線部分の面積を求めましょう。
2⃣下の図は、三角形ABCを、点Cを中心として矢印の方向に回転させ、辺BCと辺CA’が一直線になるように三角形A’B’Cをつくったものです。このとき、斜線部の面積を求めましょう。
3⃣下の図は、AB=4㎝、BC=3㎝、CA=5㎝の三角形ABCを点Cを中心として90°回転させて、三角形A’B’Cに移したものです。
斜線部分の面積を求めましょう。
*図は動画内参照
インド式計算 汎用性のある技

単元:
#計算と数の性質#いろいろな計算
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{array}{r}
32 \\[-3pt]
\underline{\times\phantom{0}56}\\[-3pt]
\end{array}$
$\begin{array}{r}
63 \\[-3pt]
\underline{\times\phantom{0}52}\\[-3pt]
\end{array}$
$\begin{array}{r}
46 \\[-3pt]
\underline{\times\phantom{0}78}\\[-3pt]
\end{array}$
$\begin{array}{r}
ab \\[-3pt]
\underline{\times\phantom{0}cd}\\[-3pt]
\end{array}$
$(10a+b)(10c+d)$
この動画を見る
$\begin{array}{r}
32 \\[-3pt]
\underline{\times\phantom{0}56}\\[-3pt]
\end{array}$
$\begin{array}{r}
63 \\[-3pt]
\underline{\times\phantom{0}52}\\[-3pt]
\end{array}$
$\begin{array}{r}
46 \\[-3pt]
\underline{\times\phantom{0}78}\\[-3pt]
\end{array}$
$\begin{array}{r}
ab \\[-3pt]
\underline{\times\phantom{0}cd}\\[-3pt]
\end{array}$
$(10a+b)(10c+d)$
【中学受験算数】【相似の利用】ゼロから始める中学受験算数43 きっちり分かる!相似の利用!!

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#平面図形#相似と相似を利用した問題
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)縮尺$\frac{1}{2500}$の地図上で、8㎝の直線道路の長さは、実際には何m?
(2)縮尺$\frac{1}{50000}$の地図上で、面積が4㎠の土地があります。この土地の実際の面積は、何㎢ありますか。
2⃣地面に垂直に立てた長さ1mの棒のかげの長さは1.8mでした。
このとき、そばに立っていた木のかげの長さは7.2mでした。
この木の高さは何mありますか。
3⃣地面に垂直に立てた長さ1mの棒のかげの長さは1.6mでした。
このとき、次の問いに答えましょう。
(1)校庭のポールの高さは6.5mです。かげの長さは何mですか。
(2)校舎のかげの長さは19.2mでした。校舎の高さは何mですか。
4⃣地面から高さ6mの位置に街灯があります。この街灯の真下から15m離れたところに、身長1.5mの人が立っています。この人のかげの長さは何mですか。
*図は動画内参照
この動画を見る
1⃣
(1)縮尺$\frac{1}{2500}$の地図上で、8㎝の直線道路の長さは、実際には何m?
(2)縮尺$\frac{1}{50000}$の地図上で、面積が4㎠の土地があります。この土地の実際の面積は、何㎢ありますか。
2⃣地面に垂直に立てた長さ1mの棒のかげの長さは1.8mでした。
このとき、そばに立っていた木のかげの長さは7.2mでした。
この木の高さは何mありますか。
3⃣地面に垂直に立てた長さ1mの棒のかげの長さは1.6mでした。
このとき、次の問いに答えましょう。
(1)校庭のポールの高さは6.5mです。かげの長さは何mですか。
(2)校舎のかげの長さは19.2mでした。校舎の高さは何mですか。
4⃣地面から高さ6mの位置に街灯があります。この街灯の真下から15m離れたところに、身長1.5mの人が立っています。この人のかげの長さは何mですか。
*図は動画内参照
【中学受験算数】りんぺん比はこう解けば簡単!! ゼロから始める中学受験算数42

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図の三角形ABCの面積は120㎠で、AD:DC=2:3、BE:ED=1:2です。三角形ABEの面積は何㎠ですか。
2⃣下の図の三角形ABCで、AD:DB=3:2、AE:EC=1:2のとき、三角形ADEと三角形ABCの面積の比を最も簡単な整数の比で表しましょう。
3⃣下の図の三角形ABCで、AD:DB=3:5、AE:EC=4:5のとき、三角形ADEと三角形ABCの面積の比を最も簡単な整数の比で表しましょう。
4⃣半径6㎝の円Aと半径10㎝の円Bがあります。円Aと円Bの面積の比を最も簡単な整数の比で表しましょう。
5⃣下の図の三角形ABCで、BCとDEは平行で、AD:DB=3:2のとき、三角形ADEと三角形ABCの面積の比を最も簡単な整数の比で表しましょう。
*図は動画内参照
この動画を見る
1⃣下の図の三角形ABCの面積は120㎠で、AD:DC=2:3、BE:ED=1:2です。三角形ABEの面積は何㎠ですか。
2⃣下の図の三角形ABCで、AD:DB=3:2、AE:EC=1:2のとき、三角形ADEと三角形ABCの面積の比を最も簡単な整数の比で表しましょう。
3⃣下の図の三角形ABCで、AD:DB=3:5、AE:EC=4:5のとき、三角形ADEと三角形ABCの面積の比を最も簡単な整数の比で表しましょう。
4⃣半径6㎝の円Aと半径10㎝の円Bがあります。円Aと円Bの面積の比を最も簡単な整数の比で表しましょう。
5⃣下の図の三角形ABCで、BCとDEは平行で、AD:DB=3:2のとき、三角形ADEと三角形ABCの面積の比を最も簡単な整数の比で表しましょう。
*図は動画内参照
【中学受験算数】ピラミッド相似、リボン相似、色々な相似問題はこう解け! ゼロから始める中学受験算数41
単元:
#算数(中学受験)#数学(中学生)#中3数学#相似な図形#平面図形#相似と相似を利用した問題
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
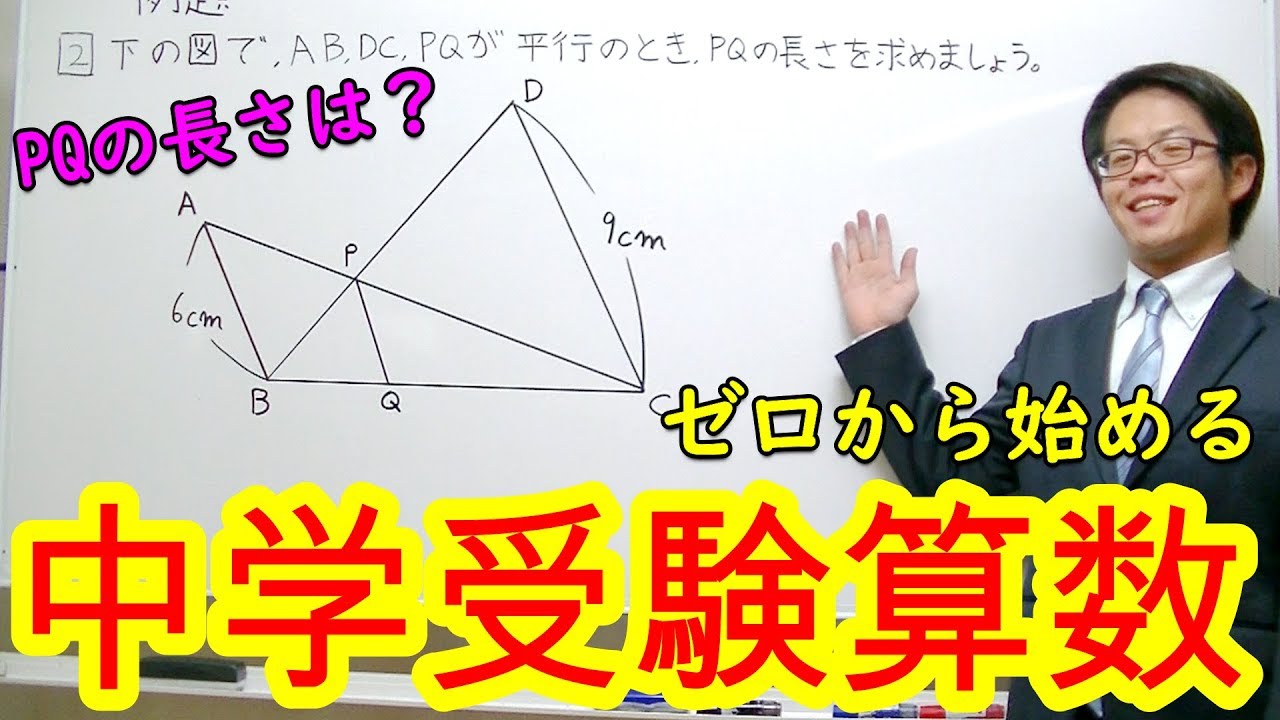
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
*図は動画内参照
この動画を見る
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
*図は動画内参照
【中学受験算数】【面積】ゼロから始める中学受験算数40 定番の図形問題を一発解決!!

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図で斜線部の面積の和を求めましょう。
2⃣下の図で斜線部の面積を求めましょう。
3⃣下の図の正方形ABCDで、㋐と㋑の部分の面積が等しいとき、CGの長さは何㎝ですか。
*図は動画内参照
この動画を見る
1⃣下の図で斜線部の面積の和を求めましょう。
2⃣下の図で斜線部の面積を求めましょう。
3⃣下の図の正方形ABCDで、㋐と㋑の部分の面積が等しいとき、CGの長さは何㎝ですか。
*図は動画内参照
【中学受験算数】【おうぎ形】ゼロから始める中学受験算数39 スッキリ解決!円と扇形!!

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣半径5㎝の円の周の長さと面積を求めましょう。
2⃣半径6㎝、中心角120°のおうぎ形の弧の長さと面積を求めましょう。
3⃣下の図のように、半径4㎝の円を並べたとき、外側の太線の長さは何㎝になりますか。
*図は動画内参照
この動画を見る
1⃣半径5㎝の円の周の長さと面積を求めましょう。
2⃣半径6㎝、中心角120°のおうぎ形の弧の長さと面積を求めましょう。
3⃣下の図のように、半径4㎝の円を並べたとき、外側の太線の長さは何㎝になりますか。
*図は動画内参照
【中学受験算数】【面積】ゼロから始める中学受験算数38 工夫して簡単に解く!面積問題!!
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣次の図形の面積を求めましょう。
(1)1辺10㎝の正方形
(2)たて6㎝、横15㎝の長方形
(3)底辺8㎝、高さ5㎝の平行四辺形
(4)底辺12㎝、高さ9㎝の三角形
(5)上底5㎝、下底9㎝、高さ6㎝の台形
(6)対角線が6㎝と8㎝のひし形
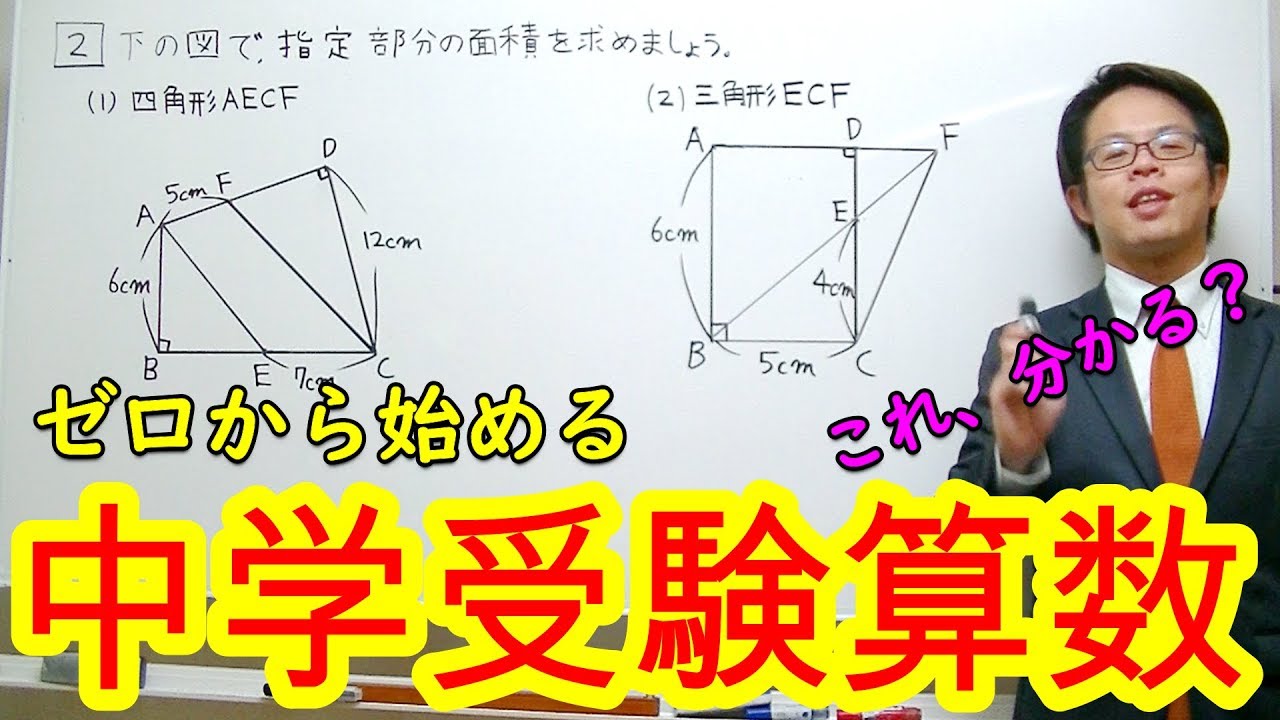
2⃣下の図で、指定部分の面積を求めましょう。
(1)四角形AECF
(2)三角形ECF
(3)四角形BEFD
(4)三角形GFD
*図は動画内参照
この動画を見る
1⃣次の図形の面積を求めましょう。
(1)1辺10㎝の正方形
(2)たて6㎝、横15㎝の長方形
(3)底辺8㎝、高さ5㎝の平行四辺形
(4)底辺12㎝、高さ9㎝の三角形
(5)上底5㎝、下底9㎝、高さ6㎝の台形
(6)対角線が6㎝と8㎝のひし形
2⃣下の図で、指定部分の面積を求めましょう。
(1)四角形AECF
(2)三角形ECF
(3)四角形BEFD
(4)三角形GFD
*図は動画内参照
【中学受験算数】【図形】ゼロから始める中学受験算数37 図形問題が苦手な方必見!角度を求める方法をキチンと解説!!

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣正八角形の1つの内角の大きさは何度ですか。
2⃣
(1)五角形の5つの内角の和は何度ですか。
(2)正十角形の1つの内角の大きさは何度ですか。
(3)正六角形の1つの外角の大きさは何度ですか。
3⃣下の図で、角xの大きさを求めましょう。
*図は動画内参照
この動画を見る
1⃣正八角形の1つの内角の大きさは何度ですか。
2⃣
(1)五角形の5つの内角の和は何度ですか。
(2)正十角形の1つの内角の大きさは何度ですか。
(3)正六角形の1つの外角の大きさは何度ですか。
3⃣下の図で、角xの大きさを求めましょう。
*図は動画内参照
【中学受験算数】【三角形】ゼロから始める中学受験算数36 図形問題が苦手な人必見!平行線と三角形の角度計算!

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図で、直線ABと直線CDが平行のとき、角xの大きさを求めましょう。
2⃣下の図で角xの大きさを求めましょう。
3⃣次の図の二等辺三角形で、角xの大きさを求めましょう。
*図は動画内参照
この動画を見る
1⃣下の図で、直線ABと直線CDが平行のとき、角xの大きさを求めましょう。
2⃣下の図で角xの大きさを求めましょう。
3⃣次の図の二等辺三角形で、角xの大きさを求めましょう。
*図は動画内参照
【中学受験算数】【順列】ゼロから始める中学受験算数35 使い分けが分かるようになる!順列と組み合わせ!!

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣A,B,C,Dの4人が横1列に並ぶとき、並び方は全部で何通りありますか。
2⃣4枚の数字カードの中から3枚を選んで並べ、3けたの整数をつくります。4枚のカードが次のとき、3けたの整数は、それぞれ全部で何通りできますか。
(1)1,2,3,4
(2)0,1,2,3
3⃣5枚の数字カードの中から3枚を選んで並べ、3けたの整数をつくります。5枚のカードが次のとき、3けたの整数は、それぞれ全部で何通りできますか。
(1)1,3,5,7,9
(2)0,2,4,6,8
4⃣次の選び方は、それぞれ全部で何通りありますか。
(1)A,B,C,D,Eの5人の中から、2人の給食当番を選ぶときの選び方
(2)F,G,H,I,Jの5人の中から、3人のそうじ当番を選ぶときの選び方
5⃣次の選び方は、それぞれ全部で何通りありますか。
(1)A,B,C,D,E,Fの6人の中から、2人のテニス選手を選ぶときの選び方
(2)L,M,N,O,P,Q,Rの7人の中から、5人のバスケットボール選手を選ぶときの選び方
この動画を見る
1⃣A,B,C,Dの4人が横1列に並ぶとき、並び方は全部で何通りありますか。
2⃣4枚の数字カードの中から3枚を選んで並べ、3けたの整数をつくります。4枚のカードが次のとき、3けたの整数は、それぞれ全部で何通りできますか。
(1)1,2,3,4
(2)0,1,2,3
3⃣5枚の数字カードの中から3枚を選んで並べ、3けたの整数をつくります。5枚のカードが次のとき、3けたの整数は、それぞれ全部で何通りできますか。
(1)1,3,5,7,9
(2)0,2,4,6,8
4⃣次の選び方は、それぞれ全部で何通りありますか。
(1)A,B,C,D,Eの5人の中から、2人の給食当番を選ぶときの選び方
(2)F,G,H,I,Jの5人の中から、3人のそうじ当番を選ぶときの選び方
5⃣次の選び方は、それぞれ全部で何通りありますか。
(1)A,B,C,D,E,Fの6人の中から、2人のテニス選手を選ぶときの選び方
(2)L,M,N,O,P,Q,Rの7人の中から、5人のバスケットボール選手を選ぶときの選び方
【中学受験算数】【場合の数】ゼロから始める中学受験算数34 簡単に解くにはコツがある!場合の数!!

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣A,B2枚の硬貨を同時に投げる時、1枚は表、1枚は裏が出る場合は何通りありますか。
2⃣図のように、A町からB町までは3本、B町からC町までは2本の道が通っています。A町からB町を通ってC町まで行く方法は、全部で何通りありますか。
3⃣大小2つのさいころを同時に投げます。次の場合は何通りか。
(1)目の数の和が7になる。
(2)目の数の積が3の倍数になる。
*図は動画内参照
この動画を見る
1⃣A,B2枚の硬貨を同時に投げる時、1枚は表、1枚は裏が出る場合は何通りありますか。
2⃣図のように、A町からB町までは3本、B町からC町までは2本の道が通っています。A町からB町を通ってC町まで行く方法は、全部で何通りありますか。
3⃣大小2つのさいころを同時に投げます。次の場合は何通りか。
(1)目の数の和が7になる。
(2)目の数の積が3の倍数になる。
*図は動画内参照
【中学受験算数】【方陣算】【集合算】【べん図】ゼロから始める中学受験算数33 パターン攻略!方陣算・集合算!!

単元:
#算数(中学受験)#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣ご石を正方形の形にしきつめます。いちばん外側のまわりの個数が60個のとき、ご石は全部で何個ありますか。
2⃣ご石を正方形の形にしきつめたら、11個あまりました。そこでたても横も1列ずつ増やそうとしたら、6個足りませんでした。
ご石は全部で何個ありますか。
3⃣35人のクラスで、国語と算数について、好ききらいのアンケートをとったところ、国語が好きな人は21人、算数が好きな人は27人、どちらも好きな人は18人でした。
(1)国語だけ好きな人は何人いますか。
(2)両方とも好きでない人は何人いますか。
4⃣あるクラスの生徒36人のうち、電車通学の人は22人、バス通学の人は19人います。どちらでもない人が6人のとき、両方を利用する人は何人ですか。
*図は動画内参照
この動画を見る
1⃣ご石を正方形の形にしきつめます。いちばん外側のまわりの個数が60個のとき、ご石は全部で何個ありますか。
2⃣ご石を正方形の形にしきつめたら、11個あまりました。そこでたても横も1列ずつ増やそうとしたら、6個足りませんでした。
ご石は全部で何個ありますか。
3⃣35人のクラスで、国語と算数について、好ききらいのアンケートをとったところ、国語が好きな人は21人、算数が好きな人は27人、どちらも好きな人は18人でした。
(1)国語だけ好きな人は何人いますか。
(2)両方とも好きでない人は何人いますか。
4⃣あるクラスの生徒36人のうち、電車通学の人は22人、バス通学の人は19人います。どちらでもない人が6人のとき、両方を利用する人は何人ですか。
*図は動画内参照
【中学受験算数】【周期算】ゼロから始める中学受験算数32 曜日と日付の簡単な導き方!!

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣ご石100個を、次のようにあるきまりで並べるとき、白のご石は何個ありますか。
○●○●○○●○●○●○○●○●○●○○●・・・
2⃣1÷7の商を小数で求めた時、小数第50位の数字は何ですか。
3⃣5月15日から数えて100日目は、何月何日ですか。
4⃣ある年の7月14日は火曜日です。
この年の10月10日は何曜日ですか。
5⃣ある年はうるう年で、2月15日は木曜日です。この時、
(1)この年の7月11日は何曜日ですか。
(2)前の年の9月20日は何曜日ですか。
この動画を見る
1⃣ご石100個を、次のようにあるきまりで並べるとき、白のご石は何個ありますか。
○●○●○○●○●○●○○●○●○●○○●・・・
2⃣1÷7の商を小数で求めた時、小数第50位の数字は何ですか。
3⃣5月15日から数えて100日目は、何月何日ですか。
4⃣ある年の7月14日は火曜日です。
この年の10月10日は何曜日ですか。
5⃣ある年はうるう年で、2月15日は木曜日です。この時、
(1)この年の7月11日は何曜日ですか。
(2)前の年の9月20日は何曜日ですか。
【中学受験算数】【植木算】ゼロから始める中学受験算数31 分かりやすく説明します!植木算!

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣長さ120mの道の片側に、木を植えることにしました。はしからはしまで、5m間かくで植えると、木は何本必要ですか。
2⃣長さ480mの道の片側に木を植えることにしました。木は何本必要ですか。
(1)はしからはしまで10m間かくで植える。
(2)一方のはしに信号機を立て、12m間かくで木を植える。
(3)両はしに信号機を立て、16m間かくで木を植える。
3⃣長さ10㎝のテープをのりしろを2㎝ずつとって15枚つなげると、全体の長さは何㎝になりますか。
4⃣長さ15㎝のテープをのりしろを2㎝ずつとって何枚かつなげる。
(1)20枚つなげると、全体の長さは何㎝か。
(2)全体の長さが171㎝になったとき、テープを何本つなげたか。
5⃣長さ3.6mの丸太を、はしから60㎝ずつに切り分けます。1回切るのに5分かかり、1回切るごとに3分休むと、全部切るのに何分かかるか。
この動画を見る
1⃣長さ120mの道の片側に、木を植えることにしました。はしからはしまで、5m間かくで植えると、木は何本必要ですか。
2⃣長さ480mの道の片側に木を植えることにしました。木は何本必要ですか。
(1)はしからはしまで10m間かくで植える。
(2)一方のはしに信号機を立て、12m間かくで木を植える。
(3)両はしに信号機を立て、16m間かくで木を植える。
3⃣長さ10㎝のテープをのりしろを2㎝ずつとって15枚つなげると、全体の長さは何㎝になりますか。
4⃣長さ15㎝のテープをのりしろを2㎝ずつとって何枚かつなげる。
(1)20枚つなげると、全体の長さは何㎝か。
(2)全体の長さが171㎝になったとき、テープを何本つなげたか。
5⃣長さ3.6mの丸太を、はしから60㎝ずつに切り分けます。1回切るのに5分かかり、1回切るごとに3分休むと、全部切るのに何分かかるか。
【中学受験算数】【時計算】【流水算】ゼロから始める中学受験算数30 時計算・流水算の簡単な解き方教えます!!

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算#点の移動・時計算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣3時40分に時計の両針が作る小さい方の角の大きさは何度ですか。
2⃣次の時刻に、時計の両針が作る小さい方の角度を求めましょう。
(1)2時30分
(2)4時10分
3⃣5時と6時の間で、時計の両針がぴったり重なるのは5時何分ですか。
4⃣8時と9時の間で、時計の両針がぴったり重なるのは8時何分ですか。
5⃣ある船が、流れのある川で、24㎞離れた2地点間を往復するのに、上りは6時間、下りは4時間かかりました。この船の静水時の速さと川の流れの速さを求めましょう。
6⃣ある船が、流れのある川で、30㎞離れた2地点間を往復するのに、上りは5時間、下りは3時間かかりました。この船の静水時の速さと川の流れの速さを求めましょう。
この動画を見る
1⃣3時40分に時計の両針が作る小さい方の角の大きさは何度ですか。
2⃣次の時刻に、時計の両針が作る小さい方の角度を求めましょう。
(1)2時30分
(2)4時10分
3⃣5時と6時の間で、時計の両針がぴったり重なるのは5時何分ですか。
4⃣8時と9時の間で、時計の両針がぴったり重なるのは8時何分ですか。
5⃣ある船が、流れのある川で、24㎞離れた2地点間を往復するのに、上りは6時間、下りは4時間かかりました。この船の静水時の速さと川の流れの速さを求めましょう。
6⃣ある船が、流れのある川で、30㎞離れた2地点間を往復するのに、上りは5時間、下りは3時間かかりました。この船の静水時の速さと川の流れの速さを求めましょう。
【中学受験算数】【通過算】ゼロから始める中学受験算数29 攻略!列車の通過算!!

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣秒速24mで走っている長さ160mの電車があります。
(1)長さ920mの鉄橋を渡りきるのに何秒かかる?
(2)長さ1480mのトンネルにかくれているのは何秒?
2⃣
(1)秒速15mで走っている長さ120mの電車があります。
長さ420mの鉄橋を渡りきるのに何秒かかる?
(2)長さ150mの電車が秒速35mで進んでいます。
長さ850mのトンネルにかくれているのは、何秒?
2⃣秒速24mで走る長さ200mの列車Aと、秒速16mで走る長さ160mの列車Bがあります。
(1)向かい合って走っている時、AとBがすれ違いのに何秒かかる?
(2)AがBを追いかける時、追いついてから追いこすのに何秒かかる?
3⃣
(1)秒速20mで走る長さ120mの列車が秒速15mで長さ90mの列車とすれ違うのに何秒かかるか。
(2)秒速22m長さ120mの列車が、秒速17m長さ80mの列車に追いつき、追いこすまでに何秒かかるか。
この動画を見る
1⃣秒速24mで走っている長さ160mの電車があります。
(1)長さ920mの鉄橋を渡りきるのに何秒かかる?
(2)長さ1480mのトンネルにかくれているのは何秒?
2⃣
(1)秒速15mで走っている長さ120mの電車があります。
長さ420mの鉄橋を渡りきるのに何秒かかる?
(2)長さ150mの電車が秒速35mで進んでいます。
長さ850mのトンネルにかくれているのは、何秒?
2⃣秒速24mで走る長さ200mの列車Aと、秒速16mで走る長さ160mの列車Bがあります。
(1)向かい合って走っている時、AとBがすれ違いのに何秒かかる?
(2)AがBを追いかける時、追いついてから追いこすのに何秒かかる?
3⃣
(1)秒速20mで走る長さ120mの列車が秒速15mで長さ90mの列車とすれ違うのに何秒かかるか。
(2)秒速22m長さ120mの列車が、秒速17m長さ80mの列車に追いつき、追いこすまでに何秒かかるか。
【受験算数】仕事算:AとBとCの3人で働けば16日で終わる仕事がある。Cが4日休めば、その分AとBが1日多く働くかBが5日多く働かなくてはならない。3人の仕事算を整理!

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
理数個別チャンネル
問題文全文(内容文):
AとBとCの3人で働けば16日で終わる仕事がある。Cが4日休めば、その分AとBが1日多く働くかBが5日多く働かなくてはならない。それぞれの仕事量は?
この動画を見る
AとBとCの3人で働けば16日で終わる仕事がある。Cが4日休めば、その分AとBが1日多く働くかBが5日多く働かなくてはならない。それぞれの仕事量は?
【受験算数】仕事算:Aで16分入れた後にBで3分入れたら満水になった。また、Aで4分入れた後にBで17分入れたら満水になった。では最初からAとB両方で入れたら何分で満水になる?

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
理数個別チャンネル
問題文全文(内容文):
Aで16分入れた後にBで3分入れたら満水になった。また、Aで4分入れた後にBで17分入れたら満水になった。では最初からAとB両方で入れたら何分で満水になる?
この動画を見る
Aで16分入れた後にBで3分入れたら満水になった。また、Aで4分入れた後にBで17分入れたら満水になった。では最初からAとB両方で入れたら何分で満水になる?
【受験算数】仕事算: AとBの2人では10日で全体の4分の1終える。残りをA1人でやったら55日かかった。A1人ですべてやると何日かかる?

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
理数個別チャンネル
問題文全文(内容文):
AとBの2人では10日で全体の4分の1終える。残りをA1人でやったら55日かかった。A1人ですべてやると何日かかる?
この動画を見る
AとBの2人では10日で全体の4分の1終える。残りをA1人でやったら55日かかった。A1人ですべてやると何日かかる?
【受験算数】仕事算:仕事算の極意を教えます!!

【中学受験算数】【旅人算】ゼロから始める中学受験算数28 これなら分かる!旅人算!!

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣800m離れたA、B間を、兄は分速85mでAから、弟は分速75mでBから同時に向かい合って出発しました。2人が出会うのは、出発してから何分後ですか。また、それはAから何m地点ですか。
2⃣1120m離れたA、B間を、姉は分速80mでAから、妹は分速60mでBから同時に向かい合って出発しました。2人が出会うのは、出発してから何分後ですか。また、それはBから何m地点ですか。
この動画を見る
1⃣800m離れたA、B間を、兄は分速85mでAから、弟は分速75mでBから同時に向かい合って出発しました。2人が出会うのは、出発してから何分後ですか。また、それはAから何m地点ですか。
2⃣1120m離れたA、B間を、姉は分速80mでAから、妹は分速60mでBから同時に向かい合って出発しました。2人が出会うのは、出発してから何分後ですか。また、それはBから何m地点ですか。
【中学受験算数】【速さと比】ゼロから始める中学受験算数27 重要単元徹底攻略!速さと比!!

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#速さ#速さその他
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)AB間を一定の速さで歩くと20分、BC間を同じ速さで歩くと30分かかるとき、AB間とBC間の道のりの比。
(2)姉が3.5㎞進む間に妹は3㎞進。姉と妹の速さの比。
(3)PQ間を歩くのに、兄は30分、弟は40分かかる。兄と弟の速さの比。
2⃣
(1)AB間の450mとBC間の600mを一定の速さで歩くとき、AB間とBC間にかかる時間の比。
(2)兄が750m歩く間に弟は500m歩いたとき、兄と弟の速さの比。
(3)PからQまでバスで1時間、電車で36分のとき、バスと電車の速さの比
3⃣
(1)AとBの歩く速さの比は3:4です。Aが20分、Bが30分歩いたとき、AとBの歩いた道のりの比を最も簡単な整数比で表せ。
(2)CとDの走った時間の比は9:8で、このときに進んだ道のりの比は15:8でした。CとDの速さの比を、最も簡単な整数比で表せ。
4⃣
(1)弟と兄の歩く速さの比は2:3です。弟が20分、兄が15分歩いたとき、弟と兄の歩いた道のりの比を最も簡単な整数比で表せ。
(2)姉と妹の走った道のりの比は8:7で、このときにかかった時間の比は4:5でした。姉と妹の速さの比を、最も簡単な整数比で表せ。
この動画を見る
1⃣
(1)AB間を一定の速さで歩くと20分、BC間を同じ速さで歩くと30分かかるとき、AB間とBC間の道のりの比。
(2)姉が3.5㎞進む間に妹は3㎞進。姉と妹の速さの比。
(3)PQ間を歩くのに、兄は30分、弟は40分かかる。兄と弟の速さの比。
2⃣
(1)AB間の450mとBC間の600mを一定の速さで歩くとき、AB間とBC間にかかる時間の比。
(2)兄が750m歩く間に弟は500m歩いたとき、兄と弟の速さの比。
(3)PからQまでバスで1時間、電車で36分のとき、バスと電車の速さの比
3⃣
(1)AとBの歩く速さの比は3:4です。Aが20分、Bが30分歩いたとき、AとBの歩いた道のりの比を最も簡単な整数比で表せ。
(2)CとDの走った時間の比は9:8で、このときに進んだ道のりの比は15:8でした。CとDの速さの比を、最も簡単な整数比で表せ。
4⃣
(1)弟と兄の歩く速さの比は2:3です。弟が20分、兄が15分歩いたとき、弟と兄の歩いた道のりの比を最も簡単な整数比で表せ。
(2)姉と妹の走った道のりの比は8:7で、このときにかかった時間の比は4:5でした。姉と妹の速さの比を、最も簡単な整数比で表せ。
【中学受験算数】【速さ】ゼロから始める中学受験算数26 最重要単元!速さの基本をスパッと解決!

単元:
#算数(中学受験)#速さ#速さその他
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)800mの道のりを16分で歩いた時の分速。
(2)時速50kmの自動車が3時間に進む道のり。
(3)1200m離れた駅まで、分速150mで行くと何分かかるか。
2⃣
(1)分速1.5km=時速$\boxed ア$km = 時速$\boxed イ$m
(2)秒速1.2m=時速 $\boxed ウ$km
3⃣
(1)秒速6m=分速▢m
(2)分速120m=時速▢km
(3)分速84m=秒速▢m
(4)時速7.5km=分速▢m
(5)秒速4m=時速▢km
(6)時速72km=秒速▢m
4⃣片道12kmの道のりを往復するのに、行きは時速6km、帰りは時速4kmで歩きました。このときの往復の平均の速さは、時速何kmですか。
この動画を見る
1⃣
(1)800mの道のりを16分で歩いた時の分速。
(2)時速50kmの自動車が3時間に進む道のり。
(3)1200m離れた駅まで、分速150mで行くと何分かかるか。
2⃣
(1)分速1.5km=時速$\boxed ア$km = 時速$\boxed イ$m
(2)秒速1.2m=時速 $\boxed ウ$km
3⃣
(1)秒速6m=分速▢m
(2)分速120m=時速▢km
(3)分速84m=秒速▢m
(4)時速7.5km=分速▢m
(5)秒速4m=時速▢km
(6)時速72km=秒速▢m
4⃣片道12kmの道のりを往復するのに、行きは時速6km、帰りは時速4kmで歩きました。このときの往復の平均の速さは、時速何kmですか。
