 三重大学
三重大学
 三重大学
三重大学
#三重大学医学部2023#極限_50

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
#三重大学医学部2023#不定積分_49
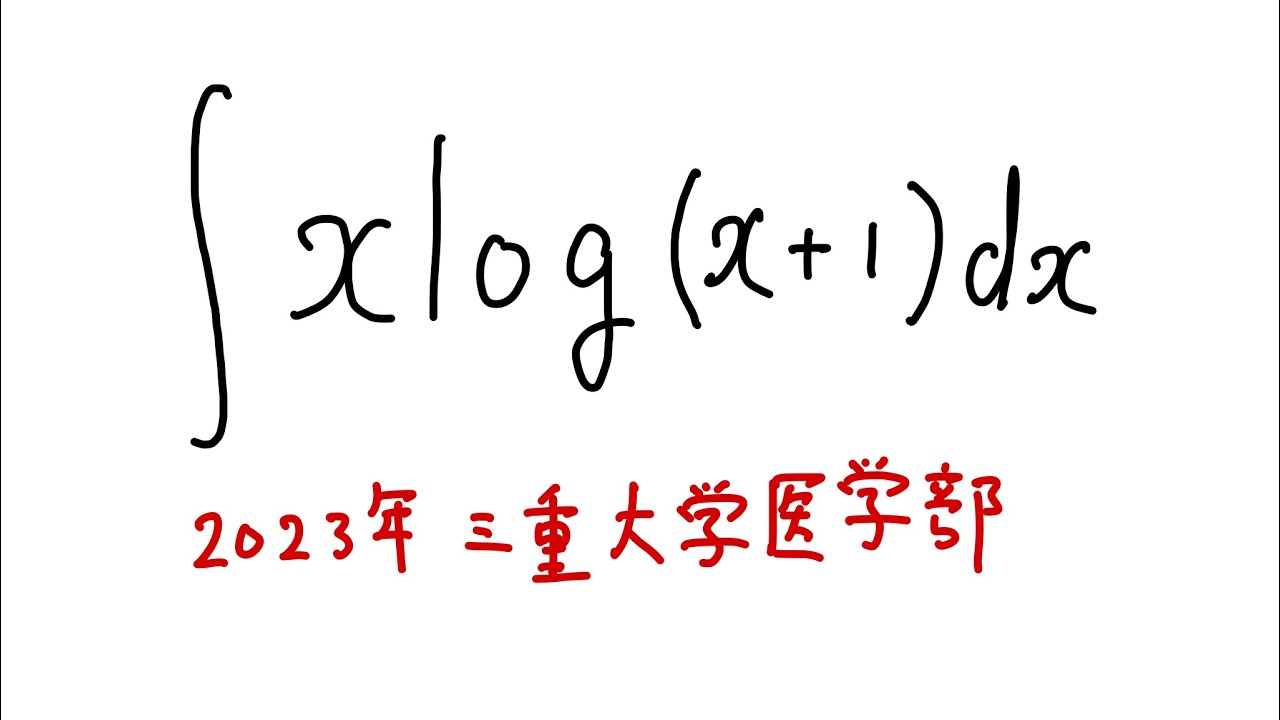
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} x \ \log (x+1)\ dx$を解け.
2023三重大学医学部過去問題
#三重大学医学部2023#不定積分_47
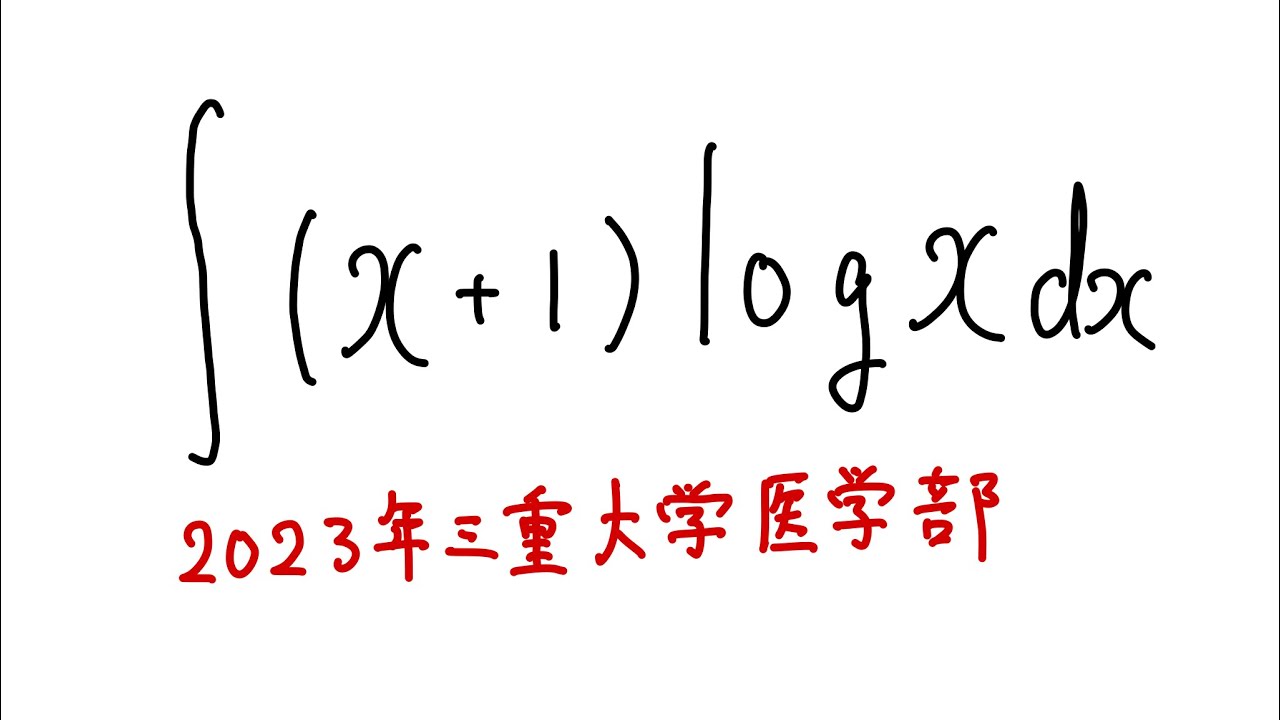
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#三重大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} (x+1)\log x \ dx$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \int_{}^{} (x+1)\log x \ dx$
を解け.
2023三重大学医学部過去問題
【高校数学】ワイエルシュトラス置換って何!?毎日積分81日目~47都道府県制覇への道~【㉔三重】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【三重大学 2009】
$\displaystyle \int_\frac{π}{3}^{\frac{π}{2}}\frac{1}{1+sinθ-cosθ}dθ$
この動画を見る
【三重大学 2009】
$\displaystyle \int_\frac{π}{3}^{\frac{π}{2}}\frac{1}{1+sinθ-cosθ}dθ$
大学入試問題#727 三重大学医学部etc (2023) 三角関数
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
ますただ
問題文全文(内容文):
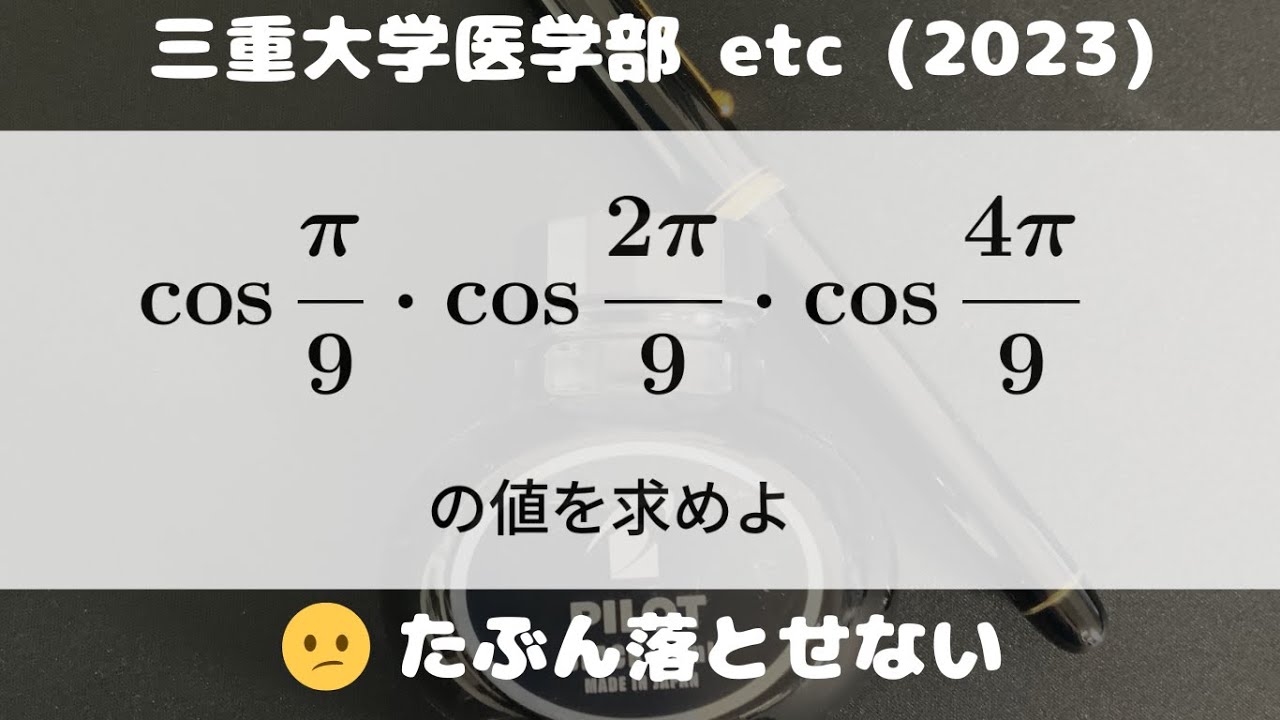
$\cos\displaystyle \frac{\pi}{9}・\cos\displaystyle \frac{2\pi}{9}・\cos\displaystyle \frac{4\pi}{9}$の値を求めよ
出典:2023年三重大学医学部 入試問題
この動画を見る
$\cos\displaystyle \frac{\pi}{9}・\cos\displaystyle \frac{2\pi}{9}・\cos\displaystyle \frac{4\pi}{9}$の値を求めよ
出典:2023年三重大学医学部 入試問題
三重大学(2016) #Shorts
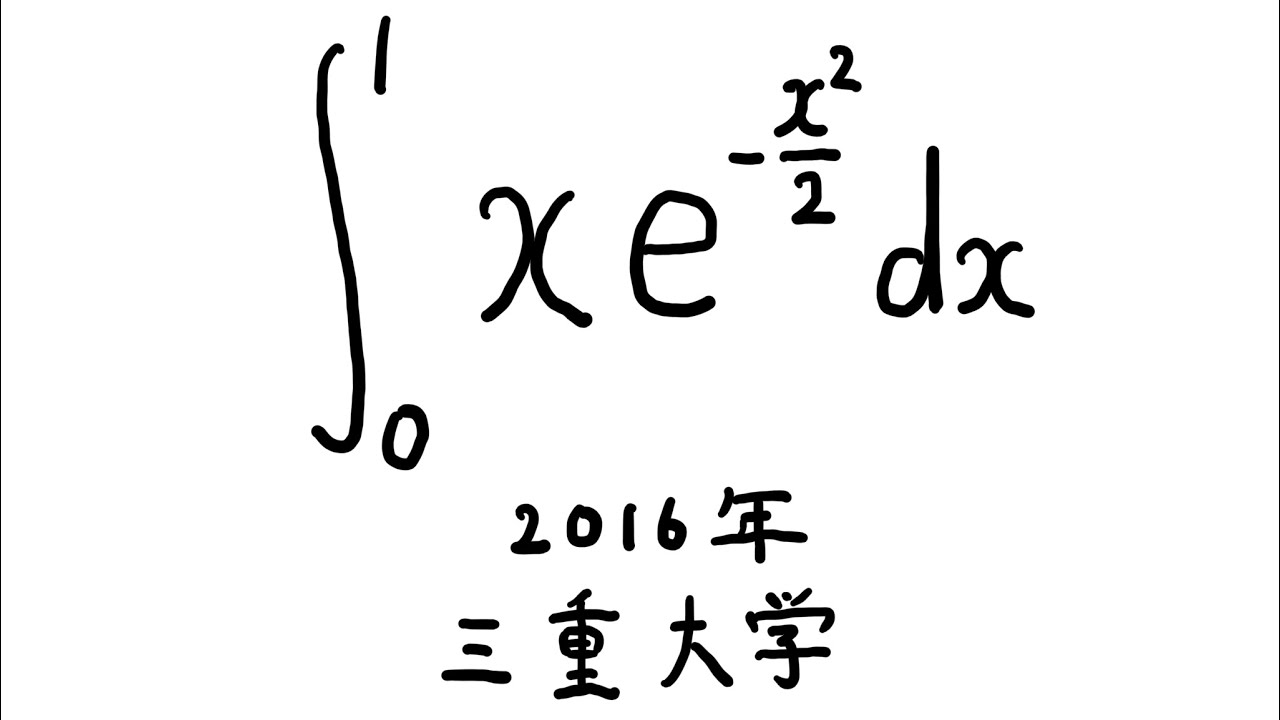
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} xe^{-\frac{1}{2}x^2} dx$
出典:2016年三重大学
この動画を見る
$\displaystyle \int_{0}^{1} xe^{-\frac{1}{2}x^2} dx$
出典:2016年三重大学
大学入試問題#147 三重大学(2020) 積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$x \geqq 1$のとき
$x \geqq 1+log\ x$を示せ
(2)
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{1+log\ x}dx \geqq \displaystyle \frac{1}{2}$を示せ
出典:2020年三重大学 入試問題
この動画を見る
(1)
$x \geqq 1$のとき
$x \geqq 1+log\ x$を示せ
(2)
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{1+log\ x}dx \geqq \displaystyle \frac{1}{2}$を示せ
出典:2020年三重大学 入試問題
数学「大学入試良問集」【13−11 ガウス記号とその戦略】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
実数$x$に対し、$[x]$を$x$以下の最大の整数とする。
たとえば、$[2]=2,\left[ \dfrac{ 7 }{ 5 } \right]=1$である。
数列$\{a_n\}$を$a_k=\left[ \dfrac{ 3k }{ 5 } \right](k=1,2,・・・)$と定めるとき、以下の問いに答えよ。
(1)$a_1,a_2,a_3,a_4,a_5$を求めよ。
(2)$a_{k+5}=a_k+3(k=1,2,・・・)$を示せ。
(3)自然数$n$に対して、$\displaystyle \sum_{k=1}^{5n} a_k$を求めよ。
この動画を見る
実数$x$に対し、$[x]$を$x$以下の最大の整数とする。
たとえば、$[2]=2,\left[ \dfrac{ 7 }{ 5 } \right]=1$である。
数列$\{a_n\}$を$a_k=\left[ \dfrac{ 3k }{ 5 } \right](k=1,2,・・・)$と定めるとき、以下の問いに答えよ。
(1)$a_1,a_2,a_3,a_4,a_5$を求めよ。
(2)$a_{k+5}=a_k+3(k=1,2,・・・)$を示せ。
(3)自然数$n$に対して、$\displaystyle \sum_{k=1}^{5n} a_k$を求めよ。
三重大2020指数不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての実数$x$に対して$2^{3x}\geqq 3・2^x-1$が成り立つ$a$の範囲を求めよ.
2020三重大過去問
この動画を見る
すべての実数$x$に対して$2^{3x}\geqq 3・2^x-1$が成り立つ$a$の範囲を求めよ.
2020三重大過去問
三重大 2変数関数の最大値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数$x,y$が$x^2+2xy+2y^2=1$を満たすとき、$2x^2+2xy+y^2$の最大値を求めよ
出典:三重大学 過去問
この動画を見る
実数$x,y$が$x^2+2xy+2y^2=1$を満たすとき、$2x^2+2xy+y^2$の最大値を求めよ
出典:三重大学 過去問
三重大 無理数の証明

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\sqrt{ 2 }$が無理数であることを証明せよ
(2)
$\sqrt{ 2 },\sqrt{ 3 },\sqrt{ 6 }$を項として含むような等差数列は存在しないことを証明せよ
出典:三重大学 過去問
この動画を見る
(1)
$\sqrt{ 2 }$が無理数であることを証明せよ
(2)
$\sqrt{ 2 },\sqrt{ 3 },\sqrt{ 6 }$を項として含むような等差数列は存在しないことを証明せよ
出典:三重大学 過去問
三重大 逆 漸化式 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=\displaystyle \frac{1}{\sqrt{ 5 }}${$(\displaystyle \frac{5+\sqrt{ 5 }}{2})^n-(\displaystyle \frac{5-\sqrt{ 5 }}{2})^n$}
(1)
$a_{n+2}$を$a_{n+1},a_{n}$を用いて表せ
(2)
$S_{n+1}$を$a_{n}$の1次式で表せ
出典:1996年三重大学 過去問
この動画を見る
$a_n=\displaystyle \frac{1}{\sqrt{ 5 }}${$(\displaystyle \frac{5+\sqrt{ 5 }}{2})^n-(\displaystyle \frac{5-\sqrt{ 5 }}{2})^n$}
(1)
$a_{n+2}$を$a_{n+1},a_{n}$を用いて表せ
(2)
$S_{n+1}$を$a_{n}$の1次式で表せ
出典:1996年三重大学 過去問
三重大 複素数 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-x+1=0$の2つの解を$\alpha, \beta$とする。
(1)
$\displaystyle \frac{1}{\alpha}+\displaystyle \frac{1}{\beta}$の値
(2)
$\alpha^{27},\beta^{27}$の値
(3)
$\alpha^n+\beta^n$の値
出典:三重大学 過去問
この動画を見る
$x^2-x+1=0$の2つの解を$\alpha, \beta$とする。
(1)
$\displaystyle \frac{1}{\alpha}+\displaystyle \frac{1}{\beta}$の値
(2)
$\alpha^{27},\beta^{27}$の値
(3)
$\alpha^n+\beta^n$の値
出典:三重大学 過去問
防衛大・三重大 漸化式 三次関数 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#数列#漸化式#防衛大学校#数学(高校生)#三重大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
防衛大学過去問題
$S_n$は初項からn項までの和
$S_n=1-(2n^2+n-1)a_n$
(1)$a_n$をnを用いて表せ。
(2)$\displaystyle\sum_{k=1}^{20}a_n$
三重大学過去問題
$f(x)=2x^3-9x^2+12x$と$y=kx$が2点のみを共有するkの値
この動画を見る
防衛大学過去問題
$S_n$は初項からn項までの和
$S_n=1-(2n^2+n-1)a_n$
(1)$a_n$をnを用いて表せ。
(2)$\displaystyle\sum_{k=1}^{20}a_n$
三重大学過去問題
$f(x)=2x^3-9x^2+12x$と$y=kx$が2点のみを共有するkの値
三重大学 対数方程式 整数解の個数 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
三重大学過去問題
$α>0$
$f(x)=log_3(-\frac{1}{2}x^2+\frac{1}{2}αx+9)$
f(x)が整数となるxが$0 \leqq x \leqq α$の範囲でちょうど6個あるようなαの範囲
この動画を見る
三重大学過去問題
$α>0$
$f(x)=log_3(-\frac{1}{2}x^2+\frac{1}{2}αx+9)$
f(x)が整数となるxが$0 \leqq x \leqq α$の範囲でちょうど6個あるようなαの範囲
三重大医)整数 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)#三重大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
三重大学
a,b,c,d素数
$f(x)=ax^3+bx^2+cx+d$
f(-1),f(0),f(1)はいずれも3で割り切れないとき、f(x)=0は整数の解をもたないことを示せ。
この動画を見る
三重大学
a,b,c,d素数
$f(x)=ax^3+bx^2+cx+d$
f(-1),f(0),f(1)はいずれも3で割り切れないとき、f(x)=0は整数の解をもたないことを示せ。
