北里大学
北里大学
福田の数学〜回転の概念を使って考えるよ〜北里大学2023年医学部第3問〜ベクトルの漸化式と点列
単元：
#大学入試過去問(数学)#平面上のベクトル#数列#ベクトルと平面図形、ベクトル方程式#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B#数C
指導講師：
福田次郎
問題文全文(内容文)：
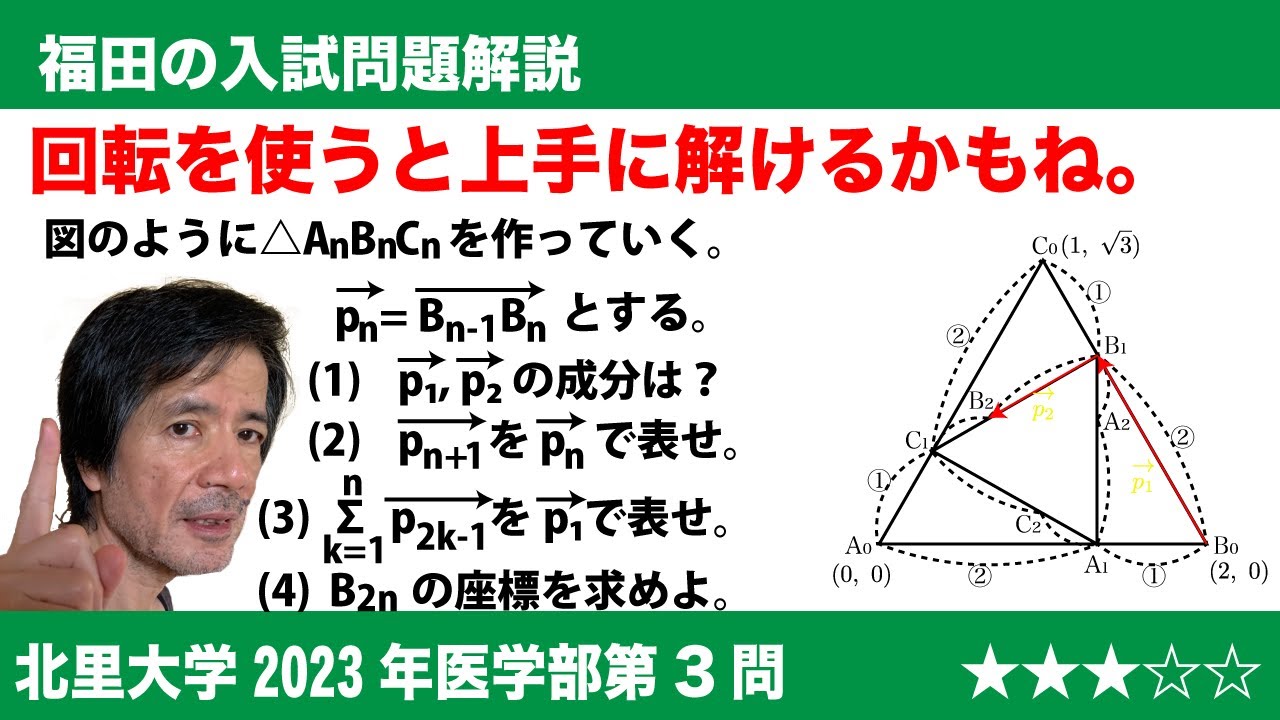
座標平面上に 3 点 $A_{0} ( 0 , 0 ), B_{0} ( 2 , 0 ), C_{0}( 1 ,\sqrt{ 3 })$があり、線分$A_{0}B_{0},B_{0}C_{0},C_{0}A_{0}$をそれぞれ 2 : 1 に内分する点 $A_{1} ,B_{1} ,C_{1}$をとる。以下同様にして、正の整数nに対し、線分$A_{n}B_{n},B_{n}C_{n},C_{n}A_{n}$をそれぞれ 2 : 1 に内分する点$A_{n+1},B_{n+1},C_{n+1}$をとる。また、$\overrightarrow{ P_{n} }=\overrightarrow{ B_{n-1}B_{n} }(n=1,2,3,・・・)$とおく。
(1)$\overrightarrow{ p_{1} },\overrightarrow{ p_{2} }$をそれぞれ成分表示せよ。
(2)$\overrightarrow{ p_{n+2} }を\overrightarrow{ p_{n} }$を用いて表せ。
(3)$\displaystyle \sum_{k=1}^n \overrightarrow{ p_{2k-1}}$を$\overrightarrow{ p-1}$を用いて表せ。
(4)点B_{2n}の座標を求めよ。
2023北里大学医過去問
この動画を見る
座標平面上に 3 点 $A_{0} ( 0 , 0 ), B_{0} ( 2 , 0 ), C_{0}( 1 ,\sqrt{ 3 })$があり、線分$A_{0}B_{0},B_{0}C_{0},C_{0}A_{0}$をそれぞれ 2 : 1 に内分する点 $A_{1} ,B_{1} ,C_{1}$をとる。以下同様にして、正の整数nに対し、線分$A_{n}B_{n},B_{n}C_{n},C_{n}A_{n}$をそれぞれ 2 : 1 に内分する点$A_{n+1},B_{n+1},C_{n+1}$をとる。また、$\overrightarrow{ P_{n} }=\overrightarrow{ B_{n-1}B_{n} }(n=1,2,3,・・・)$とおく。
(1)$\overrightarrow{ p_{1} },\overrightarrow{ p_{2} }$をそれぞれ成分表示せよ。
(2)$\overrightarrow{ p_{n+2} }を\overrightarrow{ p_{n} }$を用いて表せ。
(3)$\displaystyle \sum_{k=1}^n \overrightarrow{ p_{2k-1}}$を$\overrightarrow{ p-1}$を用いて表せ。
(4)点B_{2n}の座標を求めよ。
2023北里大学医過去問
福田の数学〜この関数にピンときたら大正解〜北里大学2023年医学部第2問〜関数の増減と方程式の実数解の個数
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
関数$f(x)=2^x-x^2$について考える。必要ならば、$0.6 \lt \log 2 \lt 0.7,-0.4 \lt \log(\log2) \lt -0.3$を用いてよい。
(1)$f(x)$は区間 $x \geqq 4$で増加することを示せ。
(2)方程式$f'(x)=0$の異なる実数解の個数を求めよ。
(3)方程式$f(x)=0$の異なる実数解の個数を求めよ。
(4)方程式$f(x)=0$の実数解のうち、最小のものを$p$とする。
この時、曲線$y=f(x)$の$x \leq 0$の部分、放物線$y=-x^2+\dfrac{2}{\log2}x$、および２つの直線$x=p,x=0$で囲まれた図形の面積を求めよ。
2023北里大学医過去問
この動画を見る
関数$f(x)=2^x-x^2$について考える。必要ならば、$0.6 \lt \log 2 \lt 0.7,-0.4 \lt \log(\log2) \lt -0.3$を用いてよい。
(1)$f(x)$は区間 $x \geqq 4$で増加することを示せ。
(2)方程式$f'(x)=0$の異なる実数解の個数を求めよ。
(3)方程式$f(x)=0$の異なる実数解の個数を求めよ。
(4)方程式$f(x)=0$の実数解のうち、最小のものを$p$とする。
この時、曲線$y=f(x)$の$x \leq 0$の部分、放物線$y=-x^2+\dfrac{2}{\log2}x$、および２つの直線$x=p,x=0$で囲まれた図形の面積を求めよ。
2023北里大学医過去問
福田の数学〜約数の個数を返す関数の性質〜北里大学2023年医学部第1問(4)〜約数の個数と整数解
単元：
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
( 4 )正の整数 N に対して、の正の約数の個数を(い)とする。例えば、12の正の約数は 1 , 2 , 3 , 4 , 6 , 12 の 6 個であるから、$f(12)= 6$である。
(i)$f(5040)=\fbox{シ}$である。
(ii)$f(k)=15$を満たす正の整数$k$のうち、 2 番目に小さいものは$\fbox{ス}$である。
(iii)大小2つのサイコロを投げるとき、出る目の積を$l$とおく。$f(l)=4$となる確率は$\fbox{セ}$である。
(iv)正の整数mとnは互いに素で、等式$f(mn)=3f(m)+5f(n)-13$を満たすとする。このとき、$mn$を最小にする$m$と$n$の組$(m,n)$は$\fbox{ソ}$である。
2023杏林大学医過去問
この動画を見る
( 4 )正の整数 N に対して、の正の約数の個数を(い)とする。例えば、12の正の約数は 1 , 2 , 3 , 4 , 6 , 12 の 6 個であるから、$f(12)= 6$である。
(i)$f(5040)=\fbox{シ}$である。
(ii)$f(k)=15$を満たす正の整数$k$のうち、 2 番目に小さいものは$\fbox{ス}$である。
(iii)大小2つのサイコロを投げるとき、出る目の積を$l$とおく。$f(l)=4$となる確率は$\fbox{セ}$である。
(iv)正の整数mとnは互いに素で、等式$f(mn)=3f(m)+5f(n)-13$を満たすとする。このとき、$mn$を最小にする$m$と$n$の組$(m,n)$は$\fbox{ソ}$である。
2023杏林大学医過去問
福田の数学〜整数部分の評価が難しい問題〜北里大学2023年医学部第1問(3)〜漸化式と整数部分の評価
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a=3+\sqrt{10},b=3-\sqrt{10}$とし、正の整数nに対して$A_n=a^n+b^n$とおく。
このとき、$A_{2} ,A_{3}$の値はそれぞれ$A_{2}=\fbox{ク},A_{3}=\fbox{ケ}$であり、
$A_{n+2}$を$A_{n+1},A_{n}$を用いて表すと$A_{n+2}=\boxed{コ}$である。
また、$a^{111}$の整数部分を$k$とするとき、kを10で割ると$\boxed{サ}$余る。
2023北里大学医過去問
この動画を見る
$a=3+\sqrt{10},b=3-\sqrt{10}$とし、正の整数nに対して$A_n=a^n+b^n$とおく。
このとき、$A_{2} ,A_{3}$の値はそれぞれ$A_{2}=\fbox{ク},A_{3}=\fbox{ケ}$であり、
$A_{n+2}$を$A_{n+1},A_{n}$を用いて表すと$A_{n+2}=\boxed{コ}$である。
また、$a^{111}$の整数部分を$k$とするとき、kを10で割ると$\boxed{サ}$余る。
2023北里大学医過去問
福田の数学〜最大値を求める問題の３連発！〜北里大学2023年医学部第1問(2)〜領域における最大値
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
点$(x,y)$は$x^2+(y-1)^2 \leqq 1$の表す領域を動くとする。
$\displaystyle \frac{x-y-1}{x+y-3}$の最大値は？
$x(y-1)$の最大値は？
$\displaystyle \frac{x^2-6x+9}{y^2-2y-3}$の最大値は？
2023北里大学医過去問
この動画を見る
点$(x,y)$は$x^2+(y-1)^2 \leqq 1$の表す領域を動くとする。
$\displaystyle \frac{x-y-1}{x+y-3}$の最大値は？
$x(y-1)$の最大値は？
$\displaystyle \frac{x^2-6x+9}{y^2-2y-3}$の最大値は？
2023北里大学医過去問
福田の数学〜格子点の個数を数えるコツ〜北里大学2023年医学部第1問(1)〜複素数平面上の円の内部にある格子点
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
( 1 ) 8 の 6 乗根のうち、実部が正で虚部が負である複素数をzとする。このとき、$\fbox{ア}$であり、$z+z^5=\fbox{イ}$。複素数平面において、点zを中心とする円Cが実軸と2点a,bで交わり、$|a-b|=\sqrt{30}$を満たしている。このとき、円Cの半径 r は$r=\fbox{ウ}$である。また、円Cの内部にある複素数のうち、実部、虚部ともに 0 以上の整数であるものの個数は$\fbox{エ}$である。
2023北里大学医過去問
この動画を見る
( 1 ) 8 の 6 乗根のうち、実部が正で虚部が負である複素数をzとする。このとき、$\fbox{ア}$であり、$z+z^5=\fbox{イ}$。複素数平面において、点zを中心とする円Cが実軸と2点a,bで交わり、$|a-b|=\sqrt{30}$を満たしている。このとき、円Cの半径 r は$r=\fbox{ウ}$である。また、円Cの内部にある複素数のうち、実部、虚部ともに 0 以上の整数であるものの個数は$\fbox{エ}$である。
2023北里大学医過去問
福田の数学〜北里大学2020年医学部第１問(1)〜虚数係数の３次方程式の解
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ (1)$p,q$を実数の定数、$i$を虚数単位とする。$x$の方程式
$x^3-(p-i)x^2+(q-pi)x-2p+\displaystyle\frac{3p}{2}i=0$
が$2+i$を解にもつとする。このとき、$p=\boxed{\ \ ア\ \ }$,$q=\boxed{\ \ イ\ \ }$である。また、この方程式の$2+i$以外の解を$\alpha$,$\beta$(ただし、|$\alpha$| $\lt$ |$\beta$|)とおくと$\left(\displaystyle\frac{\beta-i}{\alpha}\right)^7=\boxed{\ \ ウ \ \ }$である。
2020北里大学医学部過去問
この動画を見る
$\Large{\boxed{1}}$ (1)$p,q$を実数の定数、$i$を虚数単位とする。$x$の方程式
$x^3-(p-i)x^2+(q-pi)x-2p+\displaystyle\frac{3p}{2}i=0$
が$2+i$を解にもつとする。このとき、$p=\boxed{\ \ ア\ \ }$,$q=\boxed{\ \ イ\ \ }$である。また、この方程式の$2+i$以外の解を$\alpha$,$\beta$(ただし、|$\alpha$| $\lt$ |$\beta$|)とおくと$\left(\displaystyle\frac{\beta-i}{\alpha}\right)^7=\boxed{\ \ ウ \ \ }$である。
2020北里大学医学部過去問
福田の数学〜北里大学2021年医学部第３問〜関数の増減とはさみうちの原理による数列の極限
単元：
#大学入試過去問(数学)#関数と極限#微分とその応用#数列の極限#微分法#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{3}}$ 関数$f(x)=x^5-2x^3+9x$について考える。実数$t$に対して$y=f(x)$上の点($t, f(t)$)における接線と$x$軸の交点の$x$座標を$g(t)$とおく。
また、正の実数$t$に対して$h(t)=\displaystyle\frac{g(t)}{t}$とおく。次の問いに答えよ。
(1)$g(t)$を求めよ。
(2)$h'(t)=0$を満たす正の実数$t$を求めよ。
(3)実数$p$は、すべての正の実数$t$に対して|$h(t)$|$\leqq p$を満たすとする。
このような$p$の最小値を求めよ。
(4)$a$を定数とする。$a_1=a, a_{n+1}=g(a_n)$ $(n=1,2,3...)$で定められる数列
$\left\{a_n\right\}$に対して、$\displaystyle\lim_{n \to \infty}a_n=0$となることを示せ。
2021北里大学医学部過去問
この動画を見る
$\Large{\boxed{3}}$ 関数$f(x)=x^5-2x^3+9x$について考える。実数$t$に対して$y=f(x)$上の点($t, f(t)$)における接線と$x$軸の交点の$x$座標を$g(t)$とおく。
また、正の実数$t$に対して$h(t)=\displaystyle\frac{g(t)}{t}$とおく。次の問いに答えよ。
(1)$g(t)$を求めよ。
(2)$h'(t)=0$を満たす正の実数$t$を求めよ。
(3)実数$p$は、すべての正の実数$t$に対して|$h(t)$|$\leqq p$を満たすとする。
このような$p$の最小値を求めよ。
(4)$a$を定数とする。$a_1=a, a_{n+1}=g(a_n)$ $(n=1,2,3...)$で定められる数列
$\left\{a_n\right\}$に対して、$\displaystyle\lim_{n \to \infty}a_n=0$となることを示せ。
2021北里大学医学部過去問
福田の数学〜北里大学2021年医学部第２問〜条件が複雑な重複順列
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{2}}$ $n$ を正の整数とし、1,2,3,4,5,6の6個の数字から同じ数字を繰り返し用いることを許して$n$桁の整数をつくる。このような整数のうち、1が奇数個用いられるものの総数を$A_n$、それ以外のものの総数を$B_n$とする。
また、1か6がいずれも奇数個用いられるものの総数を$C_n$とする。次の問いに答えよ。
(1)$A_4$を求めよ。
(2)正の整数$n$に対して、$A_{n+1}$を$A_n$と$B_n$を用いて表せ。
(3)正の整数$n$に対して、$A_n$と$B_n$を求めよ。
(4)$p$を定数とする。$X_1=p$,$X_{n+1}=2X_n+6^n$($n$=1,2,3,...)で定められる
数列を$\left\{X_n\right\}$とする。正の整数$n$に対して、$X_n$を$n$と$p$を用いて表せ。
(5)正の整数$n$に対して、$C_n$を求めよ。
2021北里大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ $n$ を正の整数とし、1,2,3,4,5,6の6個の数字から同じ数字を繰り返し用いることを許して$n$桁の整数をつくる。このような整数のうち、1が奇数個用いられるものの総数を$A_n$、それ以外のものの総数を$B_n$とする。
また、1か6がいずれも奇数個用いられるものの総数を$C_n$とする。次の問いに答えよ。
(1)$A_4$を求めよ。
(2)正の整数$n$に対して、$A_{n+1}$を$A_n$と$B_n$を用いて表せ。
(3)正の整数$n$に対して、$A_n$と$B_n$を求めよ。
(4)$p$を定数とする。$X_1=p$,$X_{n+1}=2X_n+6^n$($n$=1,2,3,...)で定められる
数列を$\left\{X_n\right\}$とする。正の整数$n$に対して、$X_n$を$n$と$p$を用いて表せ。
(5)正の整数$n$に対して、$C_n$を求めよ。
2021北里大学医学部過去問
福田の数学〜北里大学2021年医学部第１問(4)〜定積分で表された関数と回転体の体積
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(4)関数f(x)は微分可能であり、すべての実数xについて
$f(x)=e^{2x+1}+4\int_0^xf(t)dt$
を満たすとする。関数$g(x)$を$g(x)=e^{-4x}f(x)$により定めるとき,
$g'(x)=\boxed{シ}$であり、$f(x)=\boxed{ス}$である。また、曲線$y=f(x)$と
x軸およびy軸で囲まれた図形をx軸のまわりに1回転してできる
回転体の体積は$\boxed{セ}$である。
2021北里大学医学部過去問
\end{eqnarray}
この動画を見る
(4)関数f(x)は微分可能であり、すべての実数xについて
$f(x)=e^{2x+1}+4\int_0^xf(t)dt$
を満たすとする。関数$g(x)$を$g(x)=e^{-4x}f(x)$により定めるとき,
$g'(x)=\boxed{シ}$であり、$f(x)=\boxed{ス}$である。また、曲線$y=f(x)$と
x軸およびy軸で囲まれた図形をx軸のまわりに1回転してできる
回転体の体積は$\boxed{セ}$である。
2021北里大学医学部過去問
\end{eqnarray}
福田の数学〜北里大学2021年医学部第１問(3)〜三角関数への置き換えによる最大値の求め方
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
この動画を見る
(3)$0 \leqq \theta \lt 2\pi$のとき、関数$f(\theta)=2\cos\theta(\sqrt3\sin\theta+\cos\theta)$の最大値は
$\boxed{ ケ}$である。
$g(x,y)=\frac{2\sqrt3xy+2x^2}{x^4+2x^2y^2+y^4+1}$について考える。aを正の定数とし、点(x,y)が
円$x^2+y^2=a^2$上を動くとき、g$(x,y)$の最大値はaを用いて$\boxed{コ}$と表せる。
また、点(x,y)がxy平面全体を動くとき、g(x,y)の最大値は$\boxed{サ}$である。
2021北里大学医学部過去問
北里大学2021年医学部第１問(2)。複素数平面でド・モアブルの定理を利用した偏角、絶対値の計算や正三角形の残りの頂点を求める
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
(2)iを虚数単位とし、$z_1=\frac{(\sqrt3+i)^{17}}{(1+i)^{19}(1-\sqrt3i)^7}, z_2=-1+i$とする。
$z_1$の偏角$\theta$のうち、$\\0 \leqq \theta \lt 2\pi$を満たすものは$\theta=\boxed{オ}$であり、$|z_1|=\boxed{カ}$である。
複素数平面上で$z_1,z_2$を表す点をそれぞれA,Bとする。このとき線分ABを
1辺とする正三角形ABCの、頂点Cを表す複素数の実部は0または$\boxed{キ}$である。
a,bを正の整数とし、複素数$\frac{(\sqrt3+i)^7}{(1+i)^a(1-\sqrt3i)^b}$の偏角の一つが$\frac{\pi}{12}$であるとき、
a+bの最小値は$\boxed{ク}$である。
2021北里大学医学部過去問
この動画を見る
(2)iを虚数単位とし、$z_1=\frac{(\sqrt3+i)^{17}}{(1+i)^{19}(1-\sqrt3i)^7}, z_2=-1+i$とする。
$z_1$の偏角$\theta$のうち、$\\0 \leqq \theta \lt 2\pi$を満たすものは$\theta=\boxed{オ}$であり、$|z_1|=\boxed{カ}$である。
複素数平面上で$z_1,z_2$を表す点をそれぞれA,Bとする。このとき線分ABを
1辺とする正三角形ABCの、頂点Cを表す複素数の実部は0または$\boxed{キ}$である。
a,bを正の整数とし、複素数$\frac{(\sqrt3+i)^7}{(1+i)^a(1-\sqrt3i)^b}$の偏角の一つが$\frac{\pi}{12}$であるとき、
a+bの最小値は$\boxed{ク}$である。
2021北里大学医学部過去問
福田の数学〜北里大学2021年医学部第１問(1)〜空間ベクトルの内積と平面に下ろした垂線の長さ
単元：
#数Ⅰ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と計量#三角比（三角比・拡張・相互関係・単位円）#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
(1)一辺の長さが4の正四面体ABCDにおいて、辺BCの中点をEとおく。
動点Pは$PE=\frac{1}{2}AE$を満たしながら$\triangle AED$の内部および周上を動くものとし、
$\angle PED=\theta$とおく。このとき、$\overrightarrow{ PB }・\overrightarrow{ PC }=\boxed{ア}$である。また、$\overrightarrow{ PB }・\overrightarrow{ PC }$を
$\theta$を用いて表すと$\overrightarrow{ PC }・\overrightarrow{ PD }=\boxed{イ}$、その最大値は$\boxed{ウ}$である。
$\overrightarrow{ PC }・\overrightarrow{ PD }$が最大となるときの点Pと平面ACDの距離は$\boxed{エ}$である。
2021北里大学医学部過去問
この動画を見る
(1)一辺の長さが4の正四面体ABCDにおいて、辺BCの中点をEとおく。
動点Pは$PE=\frac{1}{2}AE$を満たしながら$\triangle AED$の内部および周上を動くものとし、
$\angle PED=\theta$とおく。このとき、$\overrightarrow{ PB }・\overrightarrow{ PC }=\boxed{ア}$である。また、$\overrightarrow{ PB }・\overrightarrow{ PC }$を
$\theta$を用いて表すと$\overrightarrow{ PC }・\overrightarrow{ PD }=\boxed{イ}$、その最大値は$\boxed{ウ}$である。
$\overrightarrow{ PC }・\overrightarrow{ PD }$が最大となるときの点Pと平面ACDの距離は$\boxed{エ}$である。
2021北里大学医学部過去問
福田の数学〜北里大学2022年医学部第３問〜確率と漸化式の融合問題
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
この動画を見る
1つの箱を置ける台と2つの箱A, Bがある。箱Aには赤玉2個、青玉2個が
入っており、箱Bには白玉3個、青玉1個が入っている。台の上に箱Aを置き、
次の操作を繰り返す。
(操作) 台に置かれている箱から玉を1個取り出して色を調べてから箱に戻し、台
に置かれている箱を台から降ろす。取りだした玉が青球であれば箱Bを台
に置き、それ以外の色の玉であれば箱Aを台に置く。
正の整数nに対し、n回目の操作を終えたときに、台に箱Aが置かれている確率
をa_n、箱Bが置かれている確率をb_nとおく。次の問いに答えよ。
(1) 正の整数nに対し、$b_n$と$a_{n+1}$をそれぞれ $a_n$ を用いて表せ。
(2) 正の整数nに対し、$a_n$をnを用いて表せ。
(3) 正の整数nに対し、1回目からn回目までのn回の操作で白玉を1回も取り出
さない確率をnを用いて表せ。
(4)正の整数nに対し、1回目からn回目までのn回の操作で白玉をちょうど1回
だけ取り出す確率をnを用いて表せ。
2022北里大学医学部過去問
福田の数学〜北里大学2022年医学部第２問〜定積分と不等式
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
次の各問いに答えよ。
(1)定積分\int^1_0\frac{1}{1+x^2}dxを求めよ。
(2)$x≠0$を満たすすべての実数xに対して、$e^x \gt 1+x$と$e^{-x^2} \lt \frac{1}{1+x^2}$が
成り立つことを証明せよ。
(3)$\frac{2}{3} \lt \int^1_0e^{-x^2}dx \lt \frac{\pi}{4}$が成り立つことを証明せよ。
2022北里大学医学部過去問
この動画を見る
次の各問いに答えよ。
(1)定積分\int^1_0\frac{1}{1+x^2}dxを求めよ。
(2)$x≠0$を満たすすべての実数xに対して、$e^x \gt 1+x$と$e^{-x^2} \lt \frac{1}{1+x^2}$が
成り立つことを証明せよ。
(3)$\frac{2}{3} \lt \int^1_0e^{-x^2}dx \lt \frac{\pi}{4}$が成り立つことを証明せよ。
2022北里大学医学部過去問
福田の数学〜北里大学2022年医学部第１問(4)〜放物線と2法線で囲まれた面積の最小
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
大問1の(4)
放物線 $C:y=x^2$上に、2つの動点P(p,p²), Q (q, q²)がある。点PにおけるCの接線l₁と点 Q における C の接線l₂は垂直であり、 $p>0$であるとする。
このとき、qはpを用いてq=[ス]と表され､$l₁$と$l₂$およびCで囲まれた部分の面積Sはpを用いて S=[セ]と表される。
点PにおけるCの法線と点QにおけるCの法線の交点をRとし､ 2つの線分PRとQRおよびCで囲まれた部分の面積をTとおく。 pが正の実数全体を動くとき、Tの最小値は[ソ]である。
この動画を見る
大問1の(4)
放物線 $C:y=x^2$上に、2つの動点P(p,p²), Q (q, q²)がある。点PにおけるCの接線l₁と点 Q における C の接線l₂は垂直であり、 $p>0$であるとする。
このとき、qはpを用いてq=[ス]と表され､$l₁$と$l₂$およびCで囲まれた部分の面積Sはpを用いて S=[セ]と表される。
点PにおけるCの法線と点QにおけるCの法線の交点をRとし､ 2つの線分PRとQRおよびCで囲まれた部分の面積をTとおく。 pが正の実数全体を動くとき、Tの最小値は[ソ]である。
福田の数学〜北里大学2022年医学部第１問(3)〜不定方程式の解
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(3) 等式 $30x-23y=1$を満たす正の整数の組(x, y) のうち、$x+y$ が最小となる
ものは[キ]である。
$A={n|n$ は 600 以下の正の整数であり、30の倍数である}
$B={n|n$ は 600 以下の正の整数であり、 n を 23 で割ると4余る}
とおく。このとき、 AUBに属する正の整数の総和は[ク]である。
また、m を正の整数とし、 $∨m^2 +120$ は整数であるとすると、mのとり得る値は[ヶ],[コ],[サ],[シ]である。
2022北里大学医学部過去問
この動画を見る
(3) 等式 $30x-23y=1$を満たす正の整数の組(x, y) のうち、$x+y$ が最小となる
ものは[キ]である。
$A={n|n$ は 600 以下の正の整数であり、30の倍数である}
$B={n|n$ は 600 以下の正の整数であり、 n を 23 で割ると4余る}
とおく。このとき、 AUBに属する正の整数の総和は[ク]である。
また、m を正の整数とし、 $∨m^2 +120$ は整数であるとすると、mのとり得る値は[ヶ],[コ],[サ],[シ]である。
2022北里大学医学部過去問
福田の数学〜北里大学2022年医学部第１問(2)〜逆関数と方程式の解
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
1 (2) $f(x) = log (x/1-x)$ とする。
関数f(x) の逆関数は $f^-1 (x) = [エ]$である。
方程式$f^-1 (x) - a=0$が実数解をもつとき、 定数aのとり得る値の範囲は[オ]である。
方程式 ${f^-1(x)}²-bf^-1 (x)-3b=0$が実数解をもつとき、 定数 bのとり得る値の範囲は[カ]である。
2022北里大学医学部過去問
この動画を見る
1 (2) $f(x) = log (x/1-x)$ とする。
関数f(x) の逆関数は $f^-1 (x) = [エ]$である。
方程式$f^-1 (x) - a=0$が実数解をもつとき、 定数aのとり得る値の範囲は[オ]である。
方程式 ${f^-1(x)}²-bf^-1 (x)-3b=0$が実数解をもつとき、 定数 bのとり得る値の範囲は[カ]である。
2022北里大学医学部過去問
福田の数学〜北里大学2022年医学部第１問(1)〜複素数平面上の点の軌跡
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
1 (1)iを虚数単位とし、$α= -2+2i,β=3+i$とする。
このとき、$α^5$の値は[ア]である。
zは等式 $2|z-α| = |z-β|$を満たす複素数全体を動くとする。
このとき、複素数平面上の点P(z) が描く図形は円であり、その中心を表す複素数は[イ]である。
また、 |z| の最大値は[ウ]である。
2022北里大学医学部過去問
この動画を見る
1 (1)iを虚数単位とし、$α= -2+2i,β=3+i$とする。
このとき、$α^5$の値は[ア]である。
zは等式 $2|z-α| = |z-β|$を満たす複素数全体を動くとする。
このとき、複素数平面上の点P(z) が描く図形は円であり、その中心を表す複素数は[イ]である。
また、 |z| の最大値は[ウ]である。
2022北里大学医学部過去問
数学「大学入試良問集」【13−14 確率漸化式の基本】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
袋の中に$1～9$までの異なる数字を１つずつ書いた９枚のカードが入っている。
この中から１枚を取り出し、数字を調べて袋に戻す。
この試行を$n$回繰り返したとき、調べた$n$枚のカードの数字の和が偶数になる確率を$P_n$とする。
このとき、次の各問いに答えよ。
（1）$P_2,P_3$の値を求めよ。
（2）$P_{n+1}$を$P_n$を用いて表せ。
（3）$P_n$を$n$を用いて表せ。
この動画を見る
袋の中に$1～9$までの異なる数字を１つずつ書いた９枚のカードが入っている。
この中から１枚を取り出し、数字を調べて袋に戻す。
この試行を$n$回繰り返したとき、調べた$n$枚のカードの数字の和が偶数になる確率を$P_n$とする。
このとき、次の各問いに答えよ。
（1）$P_2,P_3$の値を求めよ。
（2）$P_{n+1}$を$P_n$を用いて表せ。
（3）$P_n$を$n$を用いて表せ。
北里大 三次関数 最大値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#北里大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a \gt 0,a \neq 1$
$f(x)=2x^3-3(a+1)x^2+6ax+1$
$0 \leqq x \leqq 2$において$f(x)$が$x=2$で最大値を取る
$a$の条件を求めよ
出典：北里大学 過去問
この動画を見る
$a \gt 0,a \neq 1$
$f(x)=2x^3-3(a+1)x^2+6ax+1$
$0 \leqq x \leqq 2$において$f(x)$が$x=2$で最大値を取る
$a$の条件を求めよ
出典：北里大学 過去問