九州大学
九州大学
福田の数学〜九州大学2024年文系第2問〜ベクトルの内積計算と三角形の面積
単元：
#大学入試過去問(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 座標平面上の原点O(0,0)、点A(2,1)を考える。点Bは第1象限にあり、|$\overrightarrow{OB}$|=$\sqrt{10}$, $\overrightarrow{OA}\bot\overrightarrow{AB}$を満たすとする。以下の問いに答えよ。
(1)点Bの座標を求めよ。
(2)$s$,$t$を正の実数とし、$\overrightarrow{OC}$=$s\overrightarrow{OA}$+$t\overrightarrow{OB}$ を満たす点Cを考える。三角形OACと三角形OBCの面積が等しく、|$\overrightarrow{OC}$|=4 が成り立つとき、$s$,$t$の値を求めよ。
この動画を見る
$\Large\boxed{2}$ 座標平面上の原点O(0,0)、点A(2,1)を考える。点Bは第1象限にあり、|$\overrightarrow{OB}$|=$\sqrt{10}$, $\overrightarrow{OA}\bot\overrightarrow{AB}$を満たすとする。以下の問いに答えよ。
(1)点Bの座標を求めよ。
(2)$s$,$t$を正の実数とし、$\overrightarrow{OC}$=$s\overrightarrow{OA}$+$t\overrightarrow{OB}$ を満たす点Cを考える。三角形OACと三角形OBCの面積が等しく、|$\overrightarrow{OC}$|=4 が成り立つとき、$s$,$t$の値を求めよ。
福田の数学〜九州大学2024年理系第4問〜3個以上の格子点を通る直線の個数
単元：
#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ $n$を3以上の整数とする。座標平面上の点のうち、$x$座標と$y$座標がともに1以上$n$以下の整数であるものを考える。これら$n^2$個の点のうち3点以上を通る直線の個数を$L(n)$とする。以下の問いに答えよ。
(1)$L(3)$を求めよ。
(2)$L(4)$を求めよ。
(3)$L(5)$を求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を3以上の整数とする。座標平面上の点のうち、$x$座標と$y$座標がともに1以上$n$以下の整数であるものを考える。これら$n^2$個の点のうち3点以上を通る直線の個数を$L(n)$とする。以下の問いに答えよ。
(1)$L(3)$を求めよ。
(2)$L(4)$を求めよ。
(3)$L(5)$を求めよ。
福田の数学〜九州大学2024年理系第3問〜階乗を含む不定方程式の解
単元：
#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)自然数$a$, $b$が$a$<$b$を満たすとき、$\displaystyle\frac{b!}{a!}$≧$b$ が成り立つことを示せ。
(2)2・$a!$=$b!$ を満たす自然数の組($a$, $b$)を全て求めよ。
(3)$a!$+$b!$=2・$c!$ を満たす自然数の組($a$, $b$, $c$)を全て求めよ。
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)自然数$a$, $b$が$a$<$b$を満たすとき、$\displaystyle\frac{b!}{a!}$≧$b$ が成り立つことを示せ。
(2)2・$a!$=$b!$ を満たす自然数の組($a$, $b$)を全て求めよ。
(3)$a!$+$b!$=2・$c!$ を満たす自然数の組($a$, $b$, $c$)を全て求めよ。
福田の数学〜九州大学2024年理系第2問〜複素数平面と高次方程式の解
単元：
#数Ⅱ#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 整式$f(z)$=$z^6$+$z^4$+$z^2$+1
について、以下の問いに答えよ。
(1)$f(z)$=0 を満たす全ての複素数$z$に対して、|$z$|=1 が成り立つことを示せ。
(2)次の条件を満たす複素数$w$を全て求めよ。
条件：$f(z)$=0 を満たす全ての複素数$z$に対して
$f(wz)$=0 が成り立つ。
この動画を見る
$\Large\boxed{2}$ 整式$f(z)$=$z^6$+$z^4$+$z^2$+1
について、以下の問いに答えよ。
(1)$f(z)$=0 を満たす全ての複素数$z$に対して、|$z$|=1 が成り立つことを示せ。
(2)次の条件を満たす複素数$w$を全て求めよ。
条件：$f(z)$=0 を満たす全ての複素数$z$に対して
$f(wz)$=0 が成り立つ。
福田の数学〜九州大学2024年理系第1問〜空間における三角形の面積の最大値
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
この動画を見る
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
福田の数学〜九州大学2023年文系第4問PART2〜確率漸化式
単元：
#数A#大学入試過去問(数学)#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
福田の数学〜九州大学2023年文系第4問PART1〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
福田の数学〜九州大学2023年文系第3問〜ベクトルの平行条件と内積
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。以下の問いに答えよ。
(1)$\overrightarrow{m}$と$\overrightarrow{n}$が平行であるための必要十分条件はD=0であることを示せ。
以下、D≠0とする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}$・$\overrightarrow{v}$=$\overrightarrow{n}$・$\overrightarrow{w}$=1, $\overrightarrow{m}$・$\overrightarrow{w}$=$\overrightarrow{n}$・$\overrightarrow{v}$=0
を満たすものを求めよ。
(3)座標平面上のベクトル$\overrightarrow{q}$に対して
$r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$
を満たす実数$r$と$s$を$\overrightarrow{q}$, $\overrightarrow{v}$, $\overrightarrow{w}$を用いて表せ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。以下の問いに答えよ。
(1)$\overrightarrow{m}$と$\overrightarrow{n}$が平行であるための必要十分条件はD=0であることを示せ。
以下、D≠0とする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}$・$\overrightarrow{v}$=$\overrightarrow{n}$・$\overrightarrow{w}$=1, $\overrightarrow{m}$・$\overrightarrow{w}$=$\overrightarrow{n}$・$\overrightarrow{v}$=0
を満たすものを求めよ。
(3)座標平面上のベクトル$\overrightarrow{q}$に対して
$r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$
を満たす実数$r$と$s$を$\overrightarrow{q}$, $\overrightarrow{v}$, $\overrightarrow{w}$を用いて表せ。
2023九州大学文系過去問
福田の数学〜九州大学2023年文系第2問〜2直線のなす角と外接円の半径
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ xy平面上の曲線C：$y$=$x^3$-$x$ を考える。変数$t$＞0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$＞0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{2}$ xy平面上の曲線C：$y$=$x^3$-$x$ を考える。変数$t$＞0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$＞0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
福田の数学〜九州大学2023年文系第１問〜放物線と直線で囲まれた面積
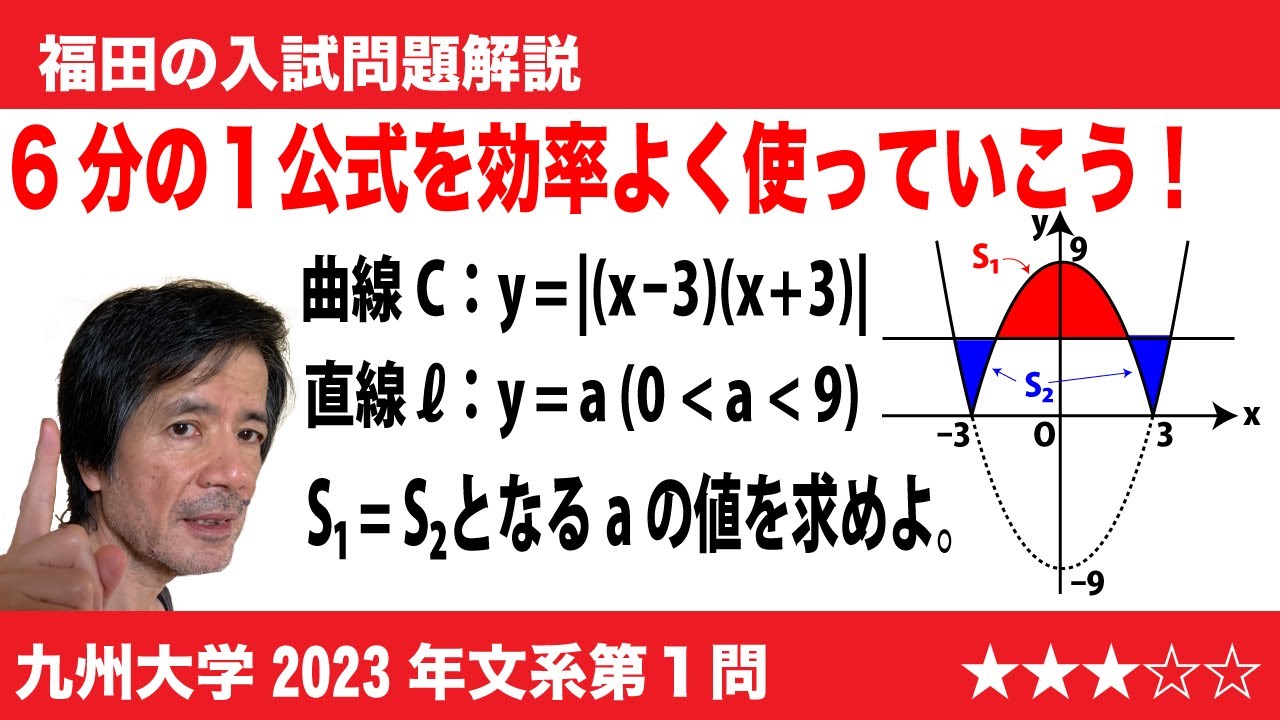
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ aを0＜a＜9 を満たす実数とする。xy平面上の曲線Cと直線lを、次のように定める。
C：$y$=|($x$-3)($x$+3)|, l：$y$=$a$
曲線Cと直線lで囲まれる図形のうち、$y$≧$a$の領域にある部分の面積を$S_1$、$y$≦$a$の領域にある部分の面積を$S_2$とする。$S_1$=$S_2$となる$a$の値を求めよ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{1}$ aを0＜a＜9 を満たす実数とする。xy平面上の曲線Cと直線lを、次のように定める。
C：$y$=|($x$-3)($x$+3)|, l：$y$=$a$
曲線Cと直線lで囲まれる図形のうち、$y$≧$a$の領域にある部分の面積を$S_1$、$y$≦$a$の領域にある部分の面積を$S_2$とする。$S_1$=$S_2$となる$a$の値を求めよ。
2023九州大学文系過去問
福田の数学〜九州大学2023年理系第5問〜媒介変数表示で表された曲線と面積
単元：
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{5}$ xy平面上の曲線Cを、媒介変数$t$を用いて次のように定める。
$x$=$t$+2$\sin^2t$, $y$=$t$+$\sin t$ (0＜$t$＜$\pi$)
以下の問いに答えよ。
(1)曲線Cに接する直線のうち$y$軸と平行なものがいくつあるか求めよ。
(2)曲線Cのうち$y$≦$x$の領域にある部分と直線$y$=$x$で囲まれた図形の面積を求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{5}$ xy平面上の曲線Cを、媒介変数$t$を用いて次のように定める。
$x$=$t$+2$\sin^2t$, $y$=$t$+$\sin t$ (0＜$t$＜$\pi$)
以下の問いに答えよ。
(1)曲線Cに接する直線のうち$y$軸と平行なものがいくつあるか求めよ。
(2)曲線Cのうち$y$≦$x$の領域にある部分と直線$y$=$x$で囲まれた図形の面積を求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第4問〜加法定理が成り立つ関数を調べるPART2
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第4問〜加法定理が成り立つ関数を調べるPART1
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{4}$ 以下の文章を読んで後の問いに答えよ。
三角関数$\cos x$, $\sin x$については加法定理が成立するが、逆に加法定理を満たす関数はどのようなものがあるだろうか。実数全体を定義域とする実数値関数$f(x)$, $g(x)$が以下の条件を満たすとする。
(A)すべてのx, yについて$f(x+y)$=$f(x)$$f(y)$-$g(x)$$g(y)$
(B)すべてのx, yについて$g(x+y)$=$f(x)$$g(y)$+$g(x)$$f(y)$
(C)$f(0)$$\ne$0
(D)$f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=0, $g'(0)$=1
条件(A), (B), (C)から$f(0)$=1, $g(0)$=0 がわかる。以上のことから$f(x)$, $g(x)$はすべてのxの値で微分可能で、$f'(x)$=$-g(x)$, $g'(x)$=$f(x)$が成立することが示される。上のことから$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 であることが、実部と虚部を調べることによりわかる。ただし$i$は虚数単位である。よって条件(A), (B), (C), (D)を満たす関数は三角関数$f(x)$=$\cos x$, $g(x)$=$\sin x$であることが示される。
さらに、a, bを実数でb≠0とする。このとき条件(D)をより一般的な(D)', $f(x)$, $g(x)$はx=0で微分可能で$f'(0)$=a, $g'(0)$=b
におきかえて、条件(A), (B), (C), (D)'を満たす$f(x)$, $g(x)$はどのような関数になるか考えてみる。この場合でも、条件(A), (B), (C)から$f(0)$=1, $g(0)$=0が上と同様にわかる。ここで
$p(x)$=$e^{-\frac{a}{b}x}f(\frac{x}{b})$, $q(x)$=$e^{-\frac{a}{b}x}g(\frac{x}{b})$
とおくと、条件(A), (B), (C), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされる。すると前半の議論により、$p(x)$, $q(x)$がまず求まり、このことを用いると$f(x)$=$\boxed{\ \ ア\ \ }$, $g(x)$=$\boxed{\ \ イ\ \ }$が得られる。
(1)下線部①について、$f(0)$=1, $g(0)$=0であることを示せ。
(2)下線部②について、$f(x)$がすべてのxの値で微分可能な関数であり、
$f'(x)$=$-g(x)$となることを示せ。
(3)下線部③について、下線部①、下線部②の事実を用いることにより、
$\left\{f(x)+ig(x)\right\}$$(\cos x-i\sin x)$=1 となることを示せ。
(4)下線部④について、条件(B), (D)において、$f(x)$を$p(x)$に、$g(x)$を$q(x)$におきかえた条件が満たされることを示せ。つまり$p(x)$を$q(x)$が、
(B)すべてのx, yについて、$q(x+y)$=$p(x)$$q(y)$+$q(x)$$p(y)$
(D)$p(x)$, $q(x)$はx=0 で微分可能で$p'(0)$=0, $q'(0)$=1
を満たすことを示せ。また空欄$\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$に入る関数を求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第3問〜ベクトルと論証PART3
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#集合と命題（集合・命題と条件・背理法）#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第3問〜ベクトルと論証PART2
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第3問〜ベクトルと論証PART1
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#集合と命題（集合・命題と条件・背理法）#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{3}$ 点Oを原点とする座標平面上の$\overrightarrow{0}$でない2つのベクトル
$\overrightarrow{m}$=($a$, $c$), $\overrightarrow{n}$=($b$, $d$)
に対して、D=ad-bc とおく。座標平面上のベクトル$\overrightarrow{q}$に対して、次の条件を考える。
条件Ⅰ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす実数r, sが存在する。
条件Ⅱ $r\overrightarrow{m}$+$s\overrightarrow{n}$=$\overrightarrow{q}$を満たす整数r, sが存在する。
以下の問いに答えよ。
(1)条件Ⅰがすべての$\overrightarrow{q}$に対して成り立つとする。D $\ne$ 0であることを示せ。
以下、D $\ne$ 0であるとする。
(2)座標平面上のベクトル$\overrightarrow{v}$, $\overrightarrow{w}$で
$\overrightarrow{m}・\overrightarrow{v}$=$\overrightarrow{n}・\overrightarrow{w}$=1, $\overrightarrow{m}・\overrightarrow{w}$=$\overrightarrow{n}・\overrightarrow{v}$=0
を満たすものを求めよ。
(3)さらにa, b, c, dが整数であるとし、x成分とy成分がともに整数であるすべてのベクトル$\overrightarrow{q}$に対して条件Ⅱが成り立つとする。Dのとりうる値をすべて求めよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第2問〜数列の収束発散の判定
単元：
#大学入試過去問(数学)#数列#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ $\alpha$を実数とする。数列$\left\{a_n\right\}$が
$a_1$=$\alpha$, $a_{n+1}$=|$a_n$-1|+$a_n$-1 (n=1,2,3,...)
で定められるとき、以下の問いに答えよ。
(1)$\alpha$≦1のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(2)$\alpha$＞2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(3)1＜$\alpha$＜$\frac{3}{2}$のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(4)$\frac{3}{2}≦\alpha$＜2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{2}$ $\alpha$を実数とする。数列$\left\{a_n\right\}$が
$a_1$=$\alpha$, $a_{n+1}$=|$a_n$-1|+$a_n$-1 (n=1,2,3,...)
で定められるとき、以下の問いに答えよ。
(1)$\alpha$≦1のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(2)$\alpha$＞2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(3)1＜$\alpha$＜$\frac{3}{2}$のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(4)$\frac{3}{2}≦\alpha$＜2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
2023九州大学理系過去問
福田の数学〜九州大学2023年理系第1問〜複素数平面上の三角形の形状
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)4次方程式$x^4$-2$x^3$+3$x^2$-2$x$+1=0 を解け。
(2)複素数平面上の$\triangle$ABCの頂点を表す複素数をそれぞれ$\alpha$, $\beta$, $\gamma$とする。
$(\alpha-\beta)^4$+$(\beta-\gamma)^4$+$(\gamma-\alpha)^4=0$
が成り立つとき、$\triangle$ABCはどのような三角形になるか答えよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)4次方程式$x^4$-2$x^3$+3$x^2$-2$x$+1=0 を解け。
(2)複素数平面上の$\triangle$ABCの頂点を表す複素数をそれぞれ$\alpha$, $\beta$, $\gamma$とする。
$(\alpha-\beta)^4$+$(\beta-\gamma)^4$+$(\gamma-\alpha)^4=0$
が成り立つとき、$\triangle$ABCはどのような三角形になるか答えよ。
2023九州大学理系過去問
2023九州大学 ４次方程式と複素平面上の三角形
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)$x^4-2x^3+3x^2-2x+1=0$を解け.
(2)複素数平面上の$\triangle ABC$の頂点を表す複素数を$\alpha,\beta,\delta$とする.
$(\alpha-\beta)^4+(\beta-\delta)+(\delta-\alpha)^4=0$が成り立つとき,$\triangle ABC$はどのような三角形か.
2023九州大過去問
この動画を見る
(1)$x^4-2x^3+3x^2-2x+1=0$を解け.
(2)複素数平面上の$\triangle ABC$の頂点を表す複素数を$\alpha,\beta,\delta$とする.
$(\alpha-\beta)^4+(\beta-\delta)+(\delta-\alpha)^4=0$が成り立つとき,$\triangle ABC$はどのような三角形か.
2023九州大過去問
福田の1.5倍速演習〜合格する重要問題067〜九州大学2017年度文系第４問〜最大公約数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{4}}$ 以下の問いに答えよ。
(1) 2017と225の最大公約数を求めよ。
(2) 225との最大公約数が15となる2017以下の自然数の個数を求めよ。
(3) 225との最大公約数が15であり、かつ1998との最大公約数が111となる2017以下の自然数を全て求めよ。
2017九州大学文系過去問
この動画を見る
$\Large{\boxed{4}}$ 以下の問いに答えよ。
(1) 2017と225の最大公約数を求めよ。
(2) 225との最大公約数が15となる2017以下の自然数の個数を求めよ。
(3) 225との最大公約数が15であり、かつ1998との最大公約数が111となる2017以下の自然数を全て求めよ。
2017九州大学文系過去問
福田の1.5倍速演習〜合格する重要問題066〜九州大学2017年度理系第３問〜等差数列の7の倍数になる項の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
この動画を見る
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
福田の1.5倍速演習〜合格する重要問題029〜九州大学2016年度理系第５問〜ドモアブルの定理と三角関数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#三角関数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
以下の問いに答えよ。
(1)$\theta$を$0 \leqq \theta \lt 2\pi$を満たす実数、iを虚数単位とし、$z=\cos\theta+i\sin\theta$で
表される複素数とする。このとき、整数nに対して次の式を証明せよ。
$\cos n\theta=\frac{1}{2}\left(z^n+\frac{1}{z^n}\right), \sin n\theta=-\frac{i}{2}\left(z^n-\frac{1}{z^n}\right)$
(2)次の方程式を満たす実数$x(0 \leqq x \lt 2\pi)$を求めよ。
$\cos x+\cos2x-\cos3x=1$
(3)次の式を証明せよ。
$\sin^220°+\sin^240°+\sin^260°+\sin^280°=\frac{9}{4}$
2016九州大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)$\theta$を$0 \leqq \theta \lt 2\pi$を満たす実数、iを虚数単位とし、$z=\cos\theta+i\sin\theta$で
表される複素数とする。このとき、整数nに対して次の式を証明せよ。
$\cos n\theta=\frac{1}{2}\left(z^n+\frac{1}{z^n}\right), \sin n\theta=-\frac{i}{2}\left(z^n-\frac{1}{z^n}\right)$
(2)次の方程式を満たす実数$x(0 \leqq x \lt 2\pi)$を求めよ。
$\cos x+\cos2x-\cos3x=1$
(3)次の式を証明せよ。
$\sin^220°+\sin^240°+\sin^260°+\sin^280°=\frac{9}{4}$
2016九州大学理系過去問
福田の1.5倍速演習〜合格する重要問題028〜九州大学2016年度文理共通問題〜余りと合同式
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#茨城大学
指導講師：
福田次郎
問題文全文(内容文)：
自然数nに対して、$10^n$を13で割った余りを$a_n$とおく。$a_n$は0から12まで
の整数である。以下の問いに答えよ。
(1)$a_{n+1}$は$10a_n$を13で割った余りに等しいことを示せ。
(2)$a_1,a_2,a_3,\cdots,a_6$を求めよ。
(3)以下の3条件を満たす自然数Nをすべて求めよ。
$(\textrm{i})N$を十進法で表示した時6桁となる。
$(\textrm{ii})N$を十進法で表示して、最初と最後の桁の数字を取り除くと
2016となる。
$(\textrm{iii})N$は13で割り切れる。
2016九州大学文理過去問
この動画を見る
自然数nに対して、$10^n$を13で割った余りを$a_n$とおく。$a_n$は0から12まで
の整数である。以下の問いに答えよ。
(1)$a_{n+1}$は$10a_n$を13で割った余りに等しいことを示せ。
(2)$a_1,a_2,a_3,\cdots,a_6$を求めよ。
(3)以下の3条件を満たす自然数Nをすべて求めよ。
$(\textrm{i})N$を十進法で表示した時6桁となる。
$(\textrm{ii})N$を十進法で表示して、最初と最後の桁の数字を取り除くと
2016となる。
$(\textrm{iii})N$は13で割り切れる。
2016九州大学文理過去問
福田の1.5倍速演習〜合格する重要問題009〜九州大学2015年度理系数学第２問〜関数の増減と区分求積
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
以下の問いに答えよ。
(1)関数$\ y=\frac{1}{x(\log x)^2}$は$x \gt 1$において単調に減少することを示せ。
(2)不定積分$\ \int\frac{1}{x(\log x)^2}dx$ を求めよ。
(3)nを3以上の整数とするとき、不等式
$\sum_{k=3}^n\frac{1}{k(\log k)^2} \lt \frac{1}{\log 2}$
が成り立つことを示せ。
2015九州大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)関数$\ y=\frac{1}{x(\log x)^2}$は$x \gt 1$において単調に減少することを示せ。
(2)不定積分$\ \int\frac{1}{x(\log x)^2}dx$ を求めよ。
(3)nを3以上の整数とするとき、不等式
$\sum_{k=3}^n\frac{1}{k(\log k)^2} \lt \frac{1}{\log 2}$
が成り立つことを示せ。
2015九州大学理系過去問
整数問題の難問！誘導ありでも難しいです【九州大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
自然数$m,n$が、$n^4=1+210m^2$ ･･･①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
この動画を見る
自然数$m,n$が、$n^4=1+210m^2$ ･･･①を満たすとき,以下の問いに答えよ。
(1)$\displaystyle \frac{n^2+1}{2},\displaystyle \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
九州大過去問
無限降下法って知ってる？整数問題の難問です【数学 入試問題】【九州大学】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
この動画を見る
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
九州大のナイスな問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
この動画を見る
$\alpha=\sqrt5-1+\sqrt{10+2\sqrt5}i$
$\beta=-\sqrt5-1+\sqrt{10-2\sqrt5}i$
(1)$\alpha$を解にもつ実数係数の2次方程式を1つ例示せよ.
(2)$\alpha,\beta$を解にもつ実数係数の4次方程式を1つ例示せよ.
(3)$\beta^5$の値を求めよ.
九州大(類)過去問
サイコロの確率の問題！注意点があります【数学 入試問題】【九州大学】
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
4個のサイコロを同時に投げるとき,出る目すべての積を$X$とする。
(1)$X$が25の倍数になる確率を求めよ。
(2)$X$が4の倍数になる確率を求めよ。
(3)$X$が100の倍数になる確率を求めよ。
九州大過去問
この動画を見る
4個のサイコロを同時に投げるとき,出る目すべての積を$X$とする。
(1)$X$が25の倍数になる確率を求めよ。
(2)$X$が4の倍数になる確率を求めよ。
(3)$X$が100の倍数になる確率を求めよ。
九州大過去問
あの公式が力を発揮する良問！微分・積分のよく出る問題です【数学 入試問題】【九州大学】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
この動画を見る
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
福田の数学〜九州大学2022年文系第４問〜定義に従って定積分の性質を証明する
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{4}}\ 定積分について述べた次の文章を読んで、後の問いに答えよ。\\
f(x)を整式とする。F'(x)=f(x)となるF(x)を1つ選び、\\
f(x)のaからbまでの定積分を\\
\int_a^bf(x)dx=F(b)-F(a) \ldots①\\
で定義する。定積分の値はF(x)の選び方によらずに定まる。\\
定積分は次の性質(A),(B),(C)をもつ。\\
(A)\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx\\
(B) a \leqq c \leqq bのとき、\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx\\
(C)区間a \leqq x \leqq bにおいてg(x) \geqq h(x)ならば、\int_a^bg(x)dx \geqq \int_a^bh(x)dx\\
ただし、f(x),g(x),h(x)は整式、k,lは定数である。\\
以下、f(x)が区間0 \leqq x \leqq 1上で増加関数になる場合を考える。\\
nを自然数とする。定積分の性質\boxed{\ \ ア\ \ }を用い、定数関数に対する定積分の計算を行うと、\\
\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②\\
が成り立つことがわかる。S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})とおくと、\\
不等式②と定積分の性質\boxed{\ \ イ\ \ }より次の不等式が成り立つ。\\
0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③\\
よって、nを限りなく大きくするとS_nは\int_0^1f(x)dxに限りなく近づく。\\
\\
\\
(1)関数F(x),G(x)が微分可能であるとき、\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)が\\
成り立つことと定積分の定義①を用いて、性質(A)でk=l=1とした場合の等式\\
\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx を示せ。\\
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。\\
a \lt bのとき、区間a \leqq x \leqq bにおいてg(x) \gt 0ならば、\int_a^bg(x)dx \gt 0\\
(3)(A),(B),(C)のうち、空欄\boxed{\ \ ア\ \ }に入る記号として最もふさわしいものを\\
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、\\
不等式②を示せ。\\
(4)(A),(B),(C)のうち、空欄\boxed{\ \ イ\ \ }に入る記号として最もふさわしいものを\\
1つ選び答えよ。また、不等式③を示せ。\\
\end{eqnarray}
2022九州大学文系過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{4}}\ 定積分について述べた次の文章を読んで、後の問いに答えよ。\\
f(x)を整式とする。F'(x)=f(x)となるF(x)を1つ選び、\\
f(x)のaからbまでの定積分を\\
\int_a^bf(x)dx=F(b)-F(a) \ldots①\\
で定義する。定積分の値はF(x)の選び方によらずに定まる。\\
定積分は次の性質(A),(B),(C)をもつ。\\
(A)\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx\\
(B) a \leqq c \leqq bのとき、\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx\\
(C)区間a \leqq x \leqq bにおいてg(x) \geqq h(x)ならば、\int_a^bg(x)dx \geqq \int_a^bh(x)dx\\
ただし、f(x),g(x),h(x)は整式、k,lは定数である。\\
以下、f(x)が区間0 \leqq x \leqq 1上で増加関数になる場合を考える。\\
nを自然数とする。定積分の性質\boxed{\ \ ア\ \ }を用い、定数関数に対する定積分の計算を行うと、\\
\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②\\
が成り立つことがわかる。S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})とおくと、\\
不等式②と定積分の性質\boxed{\ \ イ\ \ }より次の不等式が成り立つ。\\
0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③\\
よって、nを限りなく大きくするとS_nは\int_0^1f(x)dxに限りなく近づく。\\
\\
\\
(1)関数F(x),G(x)が微分可能であるとき、\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)が\\
成り立つことと定積分の定義①を用いて、性質(A)でk=l=1とした場合の等式\\
\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx を示せ。\\
(2)定積分の定義①と関数の増減と導関数の関係を用いて、次を示せ。\\
a \lt bのとき、区間a \leqq x \leqq bにおいてg(x) \gt 0ならば、\int_a^bg(x)dx \gt 0\\
(3)(A),(B),(C)のうち、空欄\boxed{\ \ ア\ \ }に入る記号として最もふさわしいものを\\
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、\\
不等式②を示せ。\\
(4)(A),(B),(C)のうち、空欄\boxed{\ \ イ\ \ }に入る記号として最もふさわしいものを\\
1つ選び答えよ。また、不等式③を示せ。\\
\end{eqnarray}
2022九州大学文系過去問