東北大学
東北大学
大学入試問題#872「受験生は一度は解くべき」 #東北大学医学部AO(2019) #極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a$を実数とする。
次の極限を求めよ。
$\displaystyle \lim_{ n \to \infty } (1+a^{2n})^{\frac{1}{n}}$
出典：2019年東北大学医学部AO
この動画を見る
$a$を実数とする。
次の極限を求めよ。
$\displaystyle \lim_{ n \to \infty } (1+a^{2n})^{\frac{1}{n}}$
出典：2019年東北大学医学部AO
大学入試問題#870「基本問題」 #東北大学医学部AO(2019) #数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$S_n=2a_n+3n$を満たす数列$\{a_n\}$の一般項$a_n$を求めよ。
出典：2019年東北大学医学部AO
この動画を見る
$S_n=2a_n+3n$を満たす数列$\{a_n\}$の一般項$a_n$を求めよ。
出典：2019年東北大学医学部AO
福田の数学〜東北大学2024年文系第2問〜75°の三角比と図形の計量
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#方べきの定理と２つの円の関係#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
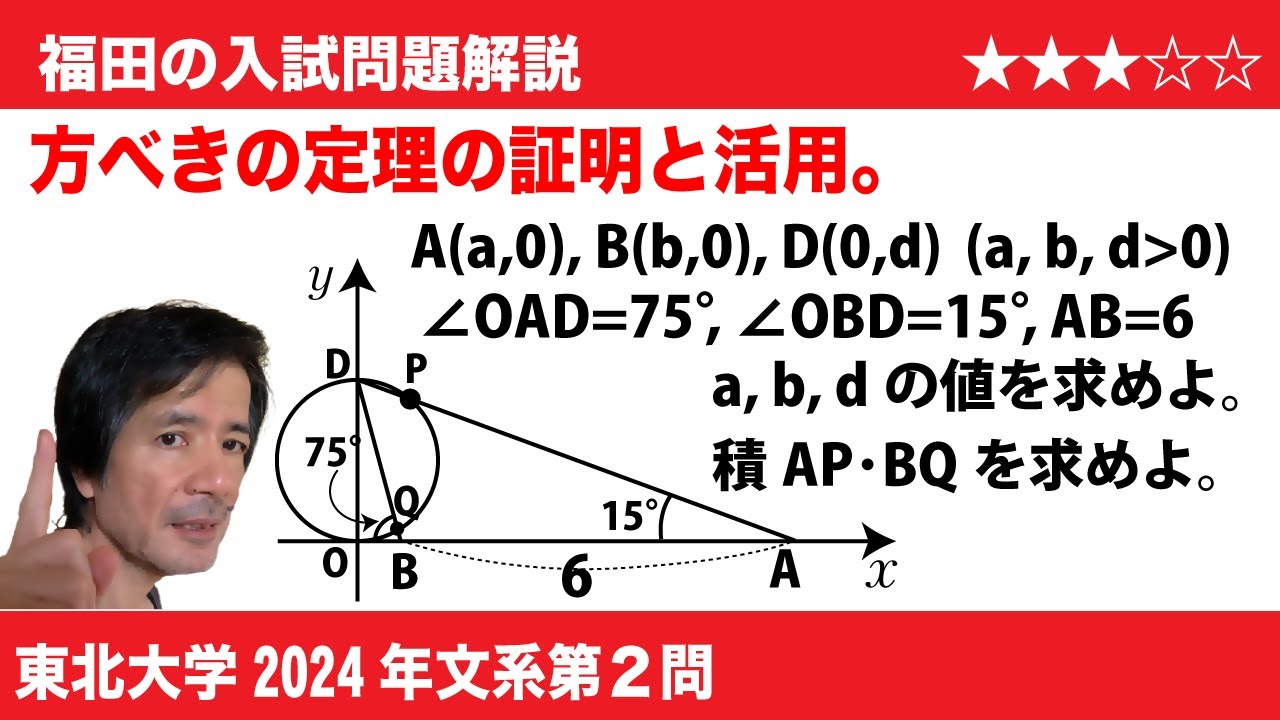
$\Large{\boxed{2}}$ $a$, $b$, $d$を正の実数とし、$xy$平面上の点O(0,0), A($a$,0), B($b$,0), D(0,$d$)が次の条件をすべて満たすとする。
$\angle OAD$=15°, $\angle OBD$=75°, AB=6
以下の問いに答えよ。
(1)$\tan 75°$の値を求めよ。
(2)$a$, $b$, $d$の値をそれぞれ求めよ。
(3)2点O, Dを直径の両端とする円をCとする。線分ADとCの交点のうちDと異なるものをPとする。また、線分BDとCの交点のうちDと異なるものをQとする。このとき、方べきの定理AP・AD=$\textrm{AO}^2$, BP・BD=$\textrm{BO}^2$ を示せ。
(4)(3)の点P,Qに対し、積AP・BQの値を求めよ。
この動画を見る
$\Large{\boxed{2}}$ $a$, $b$, $d$を正の実数とし、$xy$平面上の点O(0,0), A($a$,0), B($b$,0), D(0,$d$)が次の条件をすべて満たすとする。
$\angle OAD$=15°, $\angle OBD$=75°, AB=6
以下の問いに答えよ。
(1)$\tan 75°$の値を求めよ。
(2)$a$, $b$, $d$の値をそれぞれ求めよ。
(3)2点O, Dを直径の両端とする円をCとする。線分ADとCの交点のうちDと異なるものをPとする。また、線分BDとCの交点のうちDと異なるものをQとする。このとき、方べきの定理AP・AD=$\textrm{AO}^2$, BP・BD=$\textrm{BO}^2$ を示せ。
(4)(3)の点P,Qに対し、積AP・BQの値を求めよ。
【高校数学】東北大学2024年の積分の問題をその場で解説しながら解いてみた！毎日積分100日目~47都道府県制覇への道~【㊸宮城】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【東北大学 2024】
$xyz$空間内の$xy$平面上にある円$C:x^2+y^2=1$および円板$D:x²+y²≦1$を考える。$D$を底面とし点$P(0,0,1)$を頂点とする円錐を$K$とする。$A(0,-1,0),B(0,1,0)$とする。$xyz$空間内の平面$H:z=x$を考える。すなわち、$H$は$xz$平面上の直線$z=x$と線分$AB$をともに含む平面である。$K$の側面と$H$の交わりとしてできる曲線を$E$とする。$\displaystyle -\frac{π}{2}≦θ≦\frac{π}{2}$を満たす実数$θ$に対し、円$C$上の点$Q(cosθ,sinθ,0)$をとり、線分$PQ$と$E$の共有点を$R$とする。
(1) 線分$PR$の長さを$r(θ)$とおく。$r(θ)$を$θ$を用いて表せ。
(2)円錐$K$の側面のうち、曲線$E$の点$A$から点$R$までを結ぶ部分、線分$PA$,および線分$PR$により囲まれた部分の面積を$S(θ)$とおく。$θ$と実数$h$が条件$\displaystyle 0≦θ＜θ+h≦\frac{π}{2}$を満たすとき、次の不等式が成り立つことを示せ。
$\displaystyle \frac{h\{{r(θ)}\}^2}{2\sqrt{2}}≦S(θ+h)-S(θ)≦\frac{h\{{r(θ+h)\}}^2}{2\sqrt{2}}$
(3) 円錐$K$の側面のうち、円$C$の$x≧0$の部分と曲線$E$により囲まれた部分の面積を$T$とおく。$T$を求めよ。必要であれば$\displaystyle tan\frac{θ}{2}=u$とおく置換積分を用いてもよい。
この動画を見る
【東北大学 2024】
$xyz$空間内の$xy$平面上にある円$C:x^2+y^2=1$および円板$D:x²+y²≦1$を考える。$D$を底面とし点$P(0,0,1)$を頂点とする円錐を$K$とする。$A(0,-1,0),B(0,1,0)$とする。$xyz$空間内の平面$H:z=x$を考える。すなわち、$H$は$xz$平面上の直線$z=x$と線分$AB$をともに含む平面である。$K$の側面と$H$の交わりとしてできる曲線を$E$とする。$\displaystyle -\frac{π}{2}≦θ≦\frac{π}{2}$を満たす実数$θ$に対し、円$C$上の点$Q(cosθ,sinθ,0)$をとり、線分$PQ$と$E$の共有点を$R$とする。
(1) 線分$PR$の長さを$r(θ)$とおく。$r(θ)$を$θ$を用いて表せ。
(2)円錐$K$の側面のうち、曲線$E$の点$A$から点$R$までを結ぶ部分、線分$PA$,および線分$PR$により囲まれた部分の面積を$S(θ)$とおく。$θ$と実数$h$が条件$\displaystyle 0≦θ＜θ+h≦\frac{π}{2}$を満たすとき、次の不等式が成り立つことを示せ。
$\displaystyle \frac{h\{{r(θ)}\}^2}{2\sqrt{2}}≦S(θ+h)-S(θ)≦\frac{h\{{r(θ+h)\}}^2}{2\sqrt{2}}$
(3) 円錐$K$の側面のうち、円$C$の$x≧0$の部分と曲線$E$により囲まれた部分の面積を$T$とおく。$T$を求めよ。必要であれば$\displaystyle tan\frac{θ}{2}=u$とおく置換積分を用いてもよい。
福田の数学〜東北大学2023年文系第４問〜線分の通過範囲の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
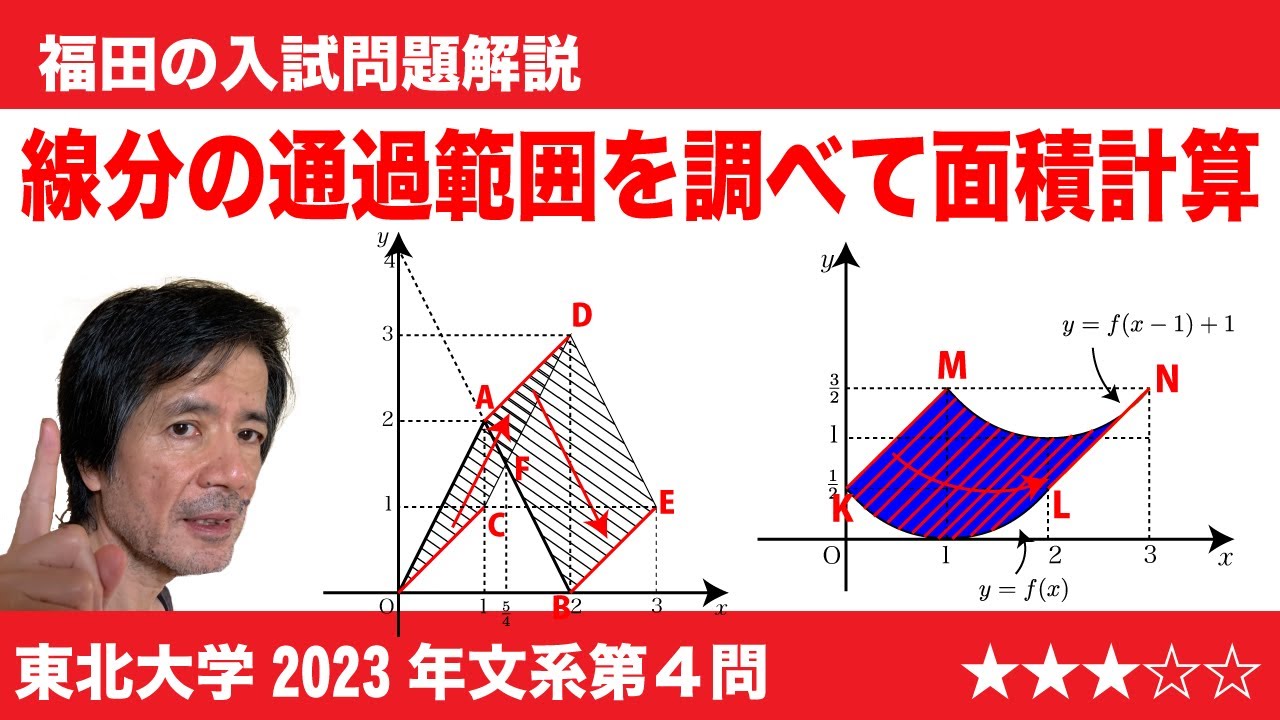
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{4}$ 関数f(x)に対して、座標平面上の2つの点P(x, f(x)), Q(x+1, f(x)+1)を考える。実数xが0≦x≦2の範囲を動くとき、線分PQがつうかしてできる図形の面積をSとおく。以下の問いに答えよ。
(1)関数f(x)=-2|x-1|+2に 対して、Sの値を求めよ。
(2)関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、曲線y=f(x)の接線で、傾きが1のものの方程式を求めよ。
(3)設問(2)の関数f(x)=$\frac{1}{2}(x-1)^2$ に対して、Sの値を求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年文系第３問〜軸の動く最大最小
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、2次関数f(x)=$x^2$+2$ax$-3 を考える。実数xがa≦x≦a+3 の範囲を動くときのf(x)の最大値および最小値を、それぞれM(a), m(a)とする。
以下の問いに答えよ。
(1)M(a)をaを用いて表せ。
(2)m(a)をaを用いて表せ。
(3)aがすべての実数を動くとき、m(a)の最小値を求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年文系第１問〜三角形の面積と内接円と外接円の半径
単元：
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#三角形の辺の比（内分・外分・二等分線）#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
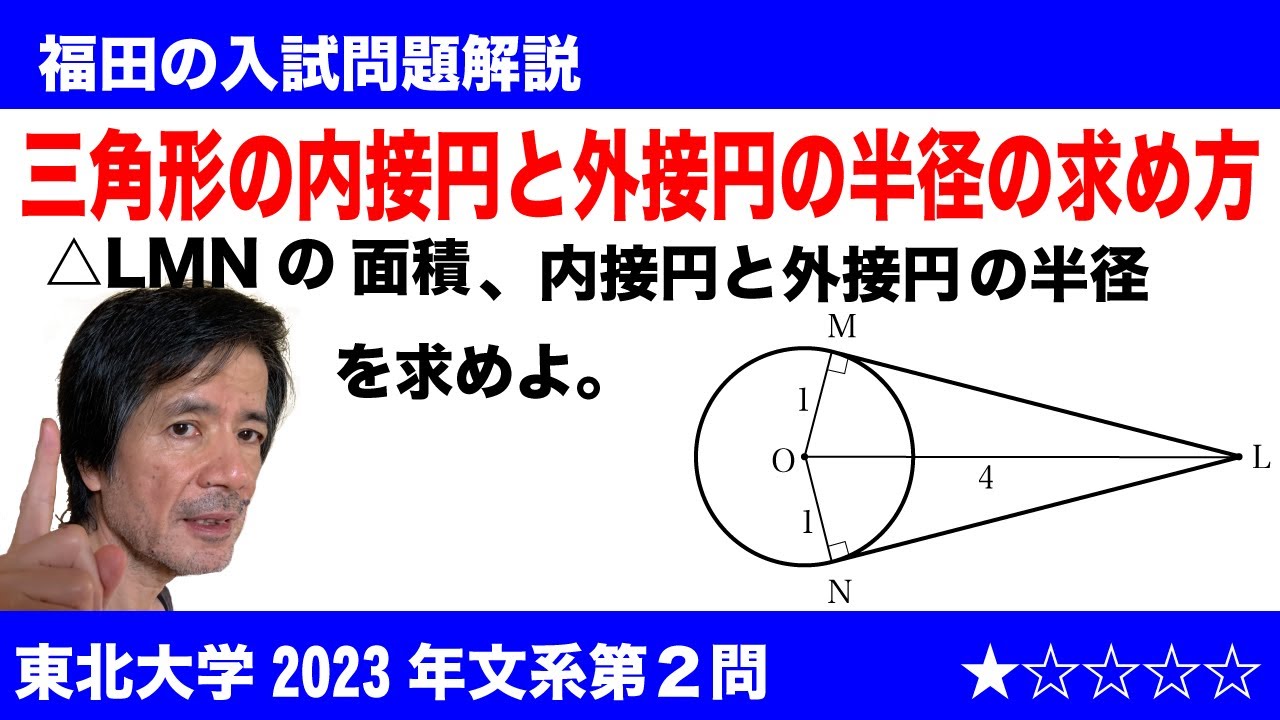
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
福田の数学〜東北大学2023年理系第６問〜線分の通過範囲の面積
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{6}$ 関数$f(x)$=$-\frac{1}{2}x$$-\frac{4}{6x+1}$について、以下の問いに答えよ。
(1)曲線y=f(x)の接線で、傾きが1であり、かつ接点のx座標が正であるものの方程式を求めよ。
(2)座標平面上の2点P(x, f(x)), Q(x+1, f(x)+1)を考える。xが0≦x≦2の範囲を動くとき、線分PQが通過してできる図形Sの概形を描け。またSの面積を求めよ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第５問〜空間ベクトルと内積
単元：
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
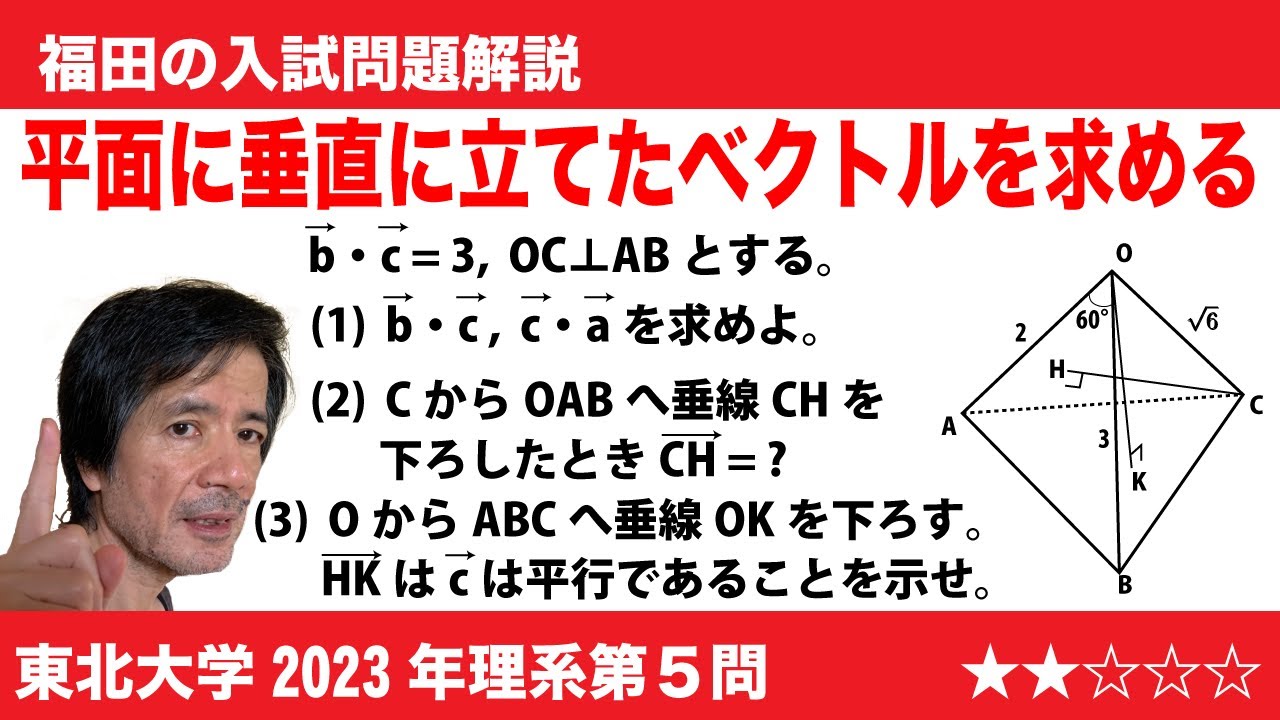
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{5}$ 四面体OABCにおいて、$\overrightarrow{a}$=$\overrightarrow{OA}$, $\overrightarrow{b}$=$\overrightarrow{OB}$, $\overrightarrow{c}$=$\overrightarrow{OC}$とおき、次が成り立つとする。
$\angle$AOB=60°, |$\overrightarrow{a}$|=2, |$\overrightarrow{b}$|=3, |$\overrightarrow{c}$|=$\sqrt 6$, $\overrightarrow{b}$・$\overrightarrow{c}$=3
ただし、$\overrightarrow{b}$・$\overrightarrow{c}$は、2つのベクトル$\overrightarrow{b}$と$\overrightarrow{c}$の内積を表す。さらに、線分OCと線分ABは垂直であるとする。点Cから3点O, A, Bを含む平面に下ろした垂線をCHとし、点Oから3点A, B, Cを含む平面に下ろした垂線をOKとする。
(1)$\overrightarrow{a}$・$\overrightarrow{b}$と$\overrightarrow{c}$・$\overrightarrow{a}$を求めよ。
(2)ベクトル$\overrightarrow{OH}$を$\overrightarrow{a}$と$\overrightarrow{b}$を用いて表せ。
(3)ベクトル$\overrightarrow{c}$とベクトル$\overrightarrow{HK}$は平行であることを示せ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第４問〜１の５乗根
単元：
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第３問〜漸化式と数列の和
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第２問〜三角方程式の解の個数とその極限
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#関数と極限#微分とその応用#関数の極限#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{2}$ 関数f(x)=$\sin3x$+$\sin x$について、以下の問いに答えよ。
(1)f(x)=0 を満たす正の実数$x$のうち、最小のものを求めよ。
(2)正の整数$m$に対して、f(x)=0を満たす正の実数$x$のうち、$m$以下のものの個数を$p(m)$とする。極限値$\displaystyle\lim_{m \to \infty}\frac{p(m)}{m}$ を求めよ。
2023東北大学理系過去問
福田の数学〜東北大学2023年理系第１問〜確率の基本性質
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 赤玉4個と白玉5個の入った、中の見えない袋がある。玉はすべて、色が区別できる他には違いはないものとする。A,Bの2人が、Aから交互に、袋から玉を1個ずつ取り出すゲームを行う。ただし取り出した玉は袋の中に戻さない。Aが赤玉を取り出したらAの勝ちとし、その時点でゲームを終了する。Bが白玉を取り出したらBの勝ちとし、その時点でゲームを終了する。袋から玉がなくなったら引き分けとし、ゲームを終了する。
(1)このゲームが引き分けとなる確率を求めよ。
(2)このゲームにAが勝つ確率を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{1}$ 赤玉4個と白玉5個の入った、中の見えない袋がある。玉はすべて、色が区別できる他には違いはないものとする。A,Bの2人が、Aから交互に、袋から玉を1個ずつ取り出すゲームを行う。ただし取り出した玉は袋の中に戻さない。Aが赤玉を取り出したらAの勝ちとし、その時点でゲームを終了する。Bが白玉を取り出したらBの勝ちとし、その時点でゲームを終了する。袋から玉がなくなったら引き分けとし、ゲームを終了する。
(1)このゲームが引き分けとなる確率を求めよ。
(2)このゲームにAが勝つ確率を求めよ。
2023東北大学理系過去問
大学入試問題#520「これは綺麗や～～」 東北大学(2023) #数列
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$a_1=S$：実数
$(n+2)a_{n+1}=n\ a_n+2$
（1）
$a_n$を求めよ
（2）
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典：2023年東北大学 入試問題
この動画を見る
$a_1=S$：実数
$(n+2)a_{n+1}=n\ a_n+2$
（1）
$a_n$を求めよ
（2）
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典：2023年東北大学 入試問題
福田の1.5倍速演習〜合格する重要問題084〜東北大学2018年度理系第４問〜三角形の内接円と外接円の半径の関係
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#三角比（三角比・拡張・相互関係・単位円）#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ 三角形ABCの内接円の半径をr, 外接円の半径をRとし、h=$\frac{r}{R}$とする。
また、$\angle$A=2α, $\angle$B=2β, $\angle$C=2γ とおく。
(1)h=4$\sin\alpha\sin\beta\sin\gamma$となることを示せ。
(2)三角形ABCが直角三角形のときh≦$\sqrt 2-1$が成り立つことを示せ。
また、等号が成り立つのはどのような場合か。
(3)一般の三角形ABCに対してh≦$\frac{1}{2}$が成り立つことを示せ。また等号が成り立つのはどのような場合か。
2018東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 三角形ABCの内接円の半径をr, 外接円の半径をRとし、h=$\frac{r}{R}$とする。
また、$\angle$A=2α, $\angle$B=2β, $\angle$C=2γ とおく。
(1)h=4$\sin\alpha\sin\beta\sin\gamma$となることを示せ。
(2)三角形ABCが直角三角形のときh≦$\sqrt 2-1$が成り立つことを示せ。
また、等号が成り立つのはどのような場合か。
(3)一般の三角形ABCに対してh≦$\frac{1}{2}$が成り立つことを示せ。また等号が成り立つのはどのような場合か。
2018東北大学理系過去問
福田の1.5倍速演習〜合格する重要問題083〜東北大学2018年度理系第１問〜直線の通過範囲
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ xy平面上における2つの放物線C：y=$(x-a)^2+b$, D：y=$-x^2$を考える。
(1)CとDが異なる2点で交わり、その2交点のx座標の差が1となるように実数a,bが動くとき、Cの頂点(a, b)の軌跡を図示せよ。
(2)実数a, bが(1)の条件を満たしながら動くとき、CとDの2交点を結ぶ直線が通過する範囲を定め、図示せよ。
2018東北大学理系過去問
この動画を見る
$\Large\boxed{1}$ xy平面上における2つの放物線C：y=$(x-a)^2+b$, D：y=$-x^2$を考える。
(1)CとDが異なる2点で交わり、その2交点のx座標の差が1となるように実数a,bが動くとき、Cの頂点(a, b)の軌跡を図示せよ。
(2)実数a, bが(1)の条件を満たしながら動くとき、CとDの2交点を結ぶ直線が通過する範囲を定め、図示せよ。
2018東北大学理系過去問
【東北大学】合格勉強法！傾向と対策、おすすめ教材と勉強法。
福田の1.5倍速演習〜合格する重要問題045〜東北大学2017年度理系第1問〜絶対値の付いた２次関数のグラフと直線の共有点の個数
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次関数とグラフ#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$を実数とする。$y=|x^2-4|$で表される曲線をCとし、
$y=ax+b$で表される直線をlとする。
(1)lが点(-2,0)を通り、lとCがちょうど3つの共有点をもつような
a,bの条件を求めよ。
(2)lとCがちょうど3つの共有点をもつような点(a,b)の軌跡を
ab平面上に図示せよ。
2017東北大学理系過去問
この動画を見る
$a,b$を実数とする。$y=|x^2-4|$で表される曲線をCとし、
$y=ax+b$で表される直線をlとする。
(1)lが点(-2,0)を通り、lとCがちょうど3つの共有点をもつような
a,bの条件を求めよ。
(2)lとCがちょうど3つの共有点をもつような点(a,b)の軌跡を
ab平面上に図示せよ。
2017東北大学理系過去問
福田の1.5倍速演習〜合格する重要問題018〜東北大学2016年度文系数学第３問〜３変数の不定方程式
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
ある工場で作る部品A,B,Cはねじをそれぞれ7個、9個、12個使っている。
出荷後に残ったこれらの部品のねじを全て外したところ、ネジが全部で54個あった。
残った部品A,B,Cの個数をそれぞれl,m,nとして可能性のある組(l,m,n)を全て求めよ。
2016東北大学文系過去問
この動画を見る
ある工場で作る部品A,B,Cはねじをそれぞれ7個、9個、12個使っている。
出荷後に残ったこれらの部品のねじを全て外したところ、ネジが全部で54個あった。
残った部品A,B,Cの個数をそれぞれl,m,nとして可能性のある組(l,m,n)を全て求めよ。
2016東北大学文系過去問
福田の1.5倍速演習〜合格する重要問題017〜東北大学2016年度理系数学第６問〜定積分で表された関数
単元：
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
関数
$f(x)=\int_0^{\pi}|\sin(t-x)-\sin2t|dt$
の区間$\ 0 \leqq x \leqq \pi\ $における最大値と最小値を求めよ。
2016東北大学理系過去問
この動画を見る
関数
$f(x)=\int_0^{\pi}|\sin(t-x)-\sin2t|dt$
の区間$\ 0 \leqq x \leqq \pi\ $における最大値と最小値を求めよ。
2016東北大学理系過去問
福田の1.5倍速演習〜合格する重要問題004〜東北大学2015年理系数学第１問
単元：
#大学入試過去問(数学)#平面上の曲線#2次曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東北大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
xy平面において、次の式が表す曲線をCとする。
$x^2+4y^2=1,x \gt 0, y \gt 0$
PをC上の点とする。PでCに接する直線をlとし、Pを通りlと垂直な直線を
mとして、x軸とy軸とmで囲まれてできる三角形の面積をSとする。PがC
上の点全体をうごくとき、Sの最大値とその時のPの座標を求めよ。
2015東北大学理系過去問
この動画を見る
xy平面において、次の式が表す曲線をCとする。
$x^2+4y^2=1,x \gt 0, y \gt 0$
PをC上の点とする。PでCに接する直線をlとし、Pを通りlと垂直な直線を
mとして、x軸とy軸とmで囲まれてできる三角形の面積をSとする。PがC
上の点全体をうごくとき、Sの最大値とその時のPの座標を求めよ。
2015東北大学理系過去問
【誘導は概要欄のリンクから】大学入試問題#294 東北大学工学部AO II期(2021) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
等差数列
$a,a+1,a+2,・・・,a+n$の和が1000となるような自然数の組$(a,n)$をすべて求めよ。
出典：2021年東北大学工学部AOⅡ期 入試問題
この動画を見る
等差数列
$a,a+1,a+2,・・・,a+n$の和が1000となるような自然数の組$(a,n)$をすべて求めよ。
出典：2021年東北大学工学部AOⅡ期 入試問題
東北大文系 虚数のナイスな問題
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#数列#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
この動画を見る
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
大学入試問題#170 東北大学(大正14年) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int log(log\ x)+\displaystyle \frac{1}{log\ x}\ dx$
出典：大正14年東北大学 入試問題
この動画を見る
$\displaystyle \int log(log\ x)+\displaystyle \frac{1}{log\ x}\ dx$
出典：大正14年東北大学 入試問題
福田の数学・入試問題解説〜東北大学2022年文系第４問〜空間における四面体の高さと体積
単元：
#数A#大学入試過去問(数学)#図形の性質#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体（オイラーの法則）#東北大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
xyz空間内の点O(0,0,0),$A(1,\sqrt2,\sqrt3),B(-\sqrt3,0,1),C(\sqrt6,-\sqrt3,\sqrt2)$
を頂点とする四面体OABCを考える。3点OABを含む平面からの距離が1の点
のうち、点Oに最も近く、x座標が正のものをHとする。
(1)Hの座標を求めよ。
(2)3点OABを含む平面と点Cの距離を求めよ。
(3)四面体OABCの体積を求めよ。
2022東北大学文系過去問
この動画を見る
xyz空間内の点O(0,0,0),$A(1,\sqrt2,\sqrt3),B(-\sqrt3,0,1),C(\sqrt6,-\sqrt3,\sqrt2)$
を頂点とする四面体OABCを考える。3点OABを含む平面からの距離が1の点
のうち、点Oに最も近く、x座標が正のものをHとする。
(1)Hの座標を求めよ。
(2)3点OABを含む平面と点Cの距離を求めよ。
(3)四面体OABCの体積を求めよ。
2022東北大学文系過去問
福田の数学〜東北大学2022年文系第３問〜領域における最大
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
a,bを正の実数とし、xy平面上の直線$l:ax;by-2=0$を考える。
(1)直線lと原点の距離が2以上であり、直線lと直線x=1の交点のy座標が
2以上であるような点(a,b)の取りうる範囲Dを求め、ab平面上に図示せよ。
(2)点(a,b)が(1)で求めた領域Dを動くとする。このとき、
$3a+2b$を最大にするa,bの値と$3a+2b$の最大値を求めよ。
2022東北大学文系過去問
この動画を見る
a,bを正の実数とし、xy平面上の直線$l:ax;by-2=0$を考える。
(1)直線lと原点の距離が2以上であり、直線lと直線x=1の交点のy座標が
2以上であるような点(a,b)の取りうる範囲Dを求め、ab平面上に図示せよ。
(2)点(a,b)が(1)で求めた領域Dを動くとする。このとき、
$3a+2b$を最大にするa,bの値と$3a+2b$の最大値を求めよ。
2022東北大学文系過去問
福田の数学・入試問題解説〜東北大学2022年文系第２問〜定積分で表された関数の最小値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#不定積分・定積分#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
実数tの関数
$F(t)=\int_0^1|x^2-t^2|dx$
について考える。
(1)$0 \leqq t \leqq 1$のとき、$F(t)$をtの整式として表せ。
(2)$t \geqq 0$ のとき、F(t)を最小にするtの値TとF(T)の値を求めよ。
2022東北大学文系過去問
この動画を見る
実数tの関数
$F(t)=\int_0^1|x^2-t^2|dx$
について考える。
(1)$0 \leqq t \leqq 1$のとき、$F(t)$をtの整式として表せ。
(2)$t \geqq 0$ のとき、F(t)を最小にするtの値TとF(T)の値を求めよ。
2022東北大学文系過去問
福田の数学・入試問題解説〜東北大学2022年理系第６問〜円柱と球の共通部分の体積
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
この動画を見る
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
大学入試問題#151 東北大学2020 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(1+x^2)^3}$を計算せよ。
出典：2020年東北大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(1+x^2)^3}$を計算せよ。
出典：2020年東北大学 入試問題
福田の数学・入試問題解説〜東北大学2022年理系第５問〜空間内の直線上の点列の極限
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
座標空間内において、ベクトル
$\overrightarrow{ a }=(1,2,1), \overrightarrow{ b }=(1,1,-1), \overrightarrow{ c }=(0,0,1)$
が定める直線
$l:s\overrightarrow{ a }, l':t\overrightarrow{ b }+\overrightarrow{ c }$
を考える。点$A_1$を原点(0,0,0)とし、点$A_1$から直線l'に下ろした垂線$A_1B_1$と
おく。次に、点$B_1(t_1\overrightarrow{ b }+\overrightarrow{ c })$から直線lに下ろした垂線を$B_1A_2$とおく。
同様に、点$A_k(s_k\overrightarrow{ a })$から直線l'に下ろした垂線を$A_kB_k$、点$B_k(t_k\overrightarrow{ b }+\overrightarrow{ c })$から直線l
に下ろした垂線を$B_kA_{k+1}$とする手順を繰り返して、点$A_n(s_n\overrightarrow{ a }),B_n(t_n\overrightarrow{ b }+\overrightarrow{ c })$
(nは正の整数)を定める。
(1)$s_n$を用いて$s_{n+1}$を表せ。
(2)極限値$S=\lim_{n \to \infty}s_n, T=\lim_{n \to \infty}t_n$を求めよ。
(3)(2)で求めたS,Tに対して、点A,Bをそれぞれ$A(S\overrightarrow{ a }),B(T\overrightarrow{ b }+\overrightarrow{ c })$とおくと、
直線ABは2直線l,l'の両方と直交することを示せ。
2022東北大学理系過去問
この動画を見る
座標空間内において、ベクトル
$\overrightarrow{ a }=(1,2,1), \overrightarrow{ b }=(1,1,-1), \overrightarrow{ c }=(0,0,1)$
が定める直線
$l:s\overrightarrow{ a }, l':t\overrightarrow{ b }+\overrightarrow{ c }$
を考える。点$A_1$を原点(0,0,0)とし、点$A_1$から直線l'に下ろした垂線$A_1B_1$と
おく。次に、点$B_1(t_1\overrightarrow{ b }+\overrightarrow{ c })$から直線lに下ろした垂線を$B_1A_2$とおく。
同様に、点$A_k(s_k\overrightarrow{ a })$から直線l'に下ろした垂線を$A_kB_k$、点$B_k(t_k\overrightarrow{ b }+\overrightarrow{ c })$から直線l
に下ろした垂線を$B_kA_{k+1}$とする手順を繰り返して、点$A_n(s_n\overrightarrow{ a }),B_n(t_n\overrightarrow{ b }+\overrightarrow{ c })$
(nは正の整数)を定める。
(1)$s_n$を用いて$s_{n+1}$を表せ。
(2)極限値$S=\lim_{n \to \infty}s_n, T=\lim_{n \to \infty}t_n$を求めよ。
(3)(2)で求めたS,Tに対して、点A,Bをそれぞれ$A(S\overrightarrow{ a }),B(T\overrightarrow{ b }+\overrightarrow{ c })$とおくと、
直線ABは2直線l,l'の両方と直交することを示せ。
2022東北大学理系過去問