 東京工業大学
東京工業大学
 東京工業大学
東京工業大学
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第5問〜分数関数のグラフと解の存在範囲

単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
(1)関数
$f(t)=\dfrac{t^2-1}{t^3} (t\neq 0)$
の増減を調べ、グラフの概形をかけ。
(2)実数$x,y,z$が、条件
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \lt y \lt z \\
xyz \neq 0 \\\
x^3y^2-x^3=x^2y^3-y^3 \\\
y^3z^2-y^3=y^2z^3-z^3
\end{array}
\right.
\end{eqnarray}$
を満たしながら動くとき、
$x$が取り得る値の範囲を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{5}$
(1)関数
$f(t)=\dfrac{t^2-1}{t^3} (t\neq 0)$
の増減を調べ、グラフの概形をかけ。
(2)実数$x,y,z$が、条件
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \lt y \lt z \\
xyz \neq 0 \\\
x^3y^2-x^3=x^2y^3-y^3 \\\
y^3z^2-y^3=y^2z^3-z^3
\end{array}
\right.
\end{eqnarray}$
を満たしながら動くとき、
$x$が取り得る値の範囲を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第4問〜フィボナッチ数列と無限級数の和

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2m}・\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{4}$
数列$\{a_n\}$を
$a_1=a_2=1,a_{n+2}=a_{n+1}+a_n (n=1,2,3,\cdots)$
により定め、数列$\{b_n\}$を
$\tan b_n=\dfrac{1}{a_n}$
により定める。
ただし、$0\lt b_n \lt \dfrac{\pi}{2}$であるものとする。
(1)$n\geqq 2$に対して、$a_{n+1}a_{n-1}-{a_n}^2$を求めよ。
(2)$m\geqq 1$($m$は整数)に対して、
$a_{2m}・\tan(b_{2m+1}+b_{2m+2})$を求めよ。
(3)無限級数$\displaystyle \sum_{m=0}^{\infty} b_{2m+1}$を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第3問〜確率漸化式と無限級数の和

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$0\lt p\lt 1$とする。
表が出る確率が$p$、裏が出る確率が$1-p$である
$1$枚のコインを使って次のゲームを行う。
・ゲームの開始時点で点数は$0$点
・コインを投げ続け、表が出るごとに$1$点加算し、
裏が出たときは点数はそのまま
・$2$回続けて裏が出たらゲームは終了。
$0$以上の整数$n$に対し、ゲームが終わったときに
$n$点となっている確率を$Q_n$とする。
(1)$Q_1,Q_2$を$p$を用いて表せ。
(2)$Q_2$を$n$と$p$を用いて表せ。
(3)$0\lt x\lt 1$を満たす実数$x$に対して次式が
成り立つことを示せ。
$\dfrac{1}{(1-x)^2}=\displaystyle \sum_{k=0}^{\infty}(n+1)x^n$
必要ならば$0\lt x \lt 1$のとき
$\displaystyle \lim_{n\to\infty} nx^n=0$であることを
証明なしで使ってもよい。
(4)無限級数$\displaystyle \sum_{n=0}^{\infty} nQn$を$p$を用いて表せ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{3}$
$0\lt p\lt 1$とする。
表が出る確率が$p$、裏が出る確率が$1-p$である
$1$枚のコインを使って次のゲームを行う。
・ゲームの開始時点で点数は$0$点
・コインを投げ続け、表が出るごとに$1$点加算し、
裏が出たときは点数はそのまま
・$2$回続けて裏が出たらゲームは終了。
$0$以上の整数$n$に対し、ゲームが終わったときに
$n$点となっている確率を$Q_n$とする。
(1)$Q_1,Q_2$を$p$を用いて表せ。
(2)$Q_2$を$n$と$p$を用いて表せ。
(3)$0\lt x\lt 1$を満たす実数$x$に対して次式が
成り立つことを示せ。
$\dfrac{1}{(1-x)^2}=\displaystyle \sum_{k=0}^{\infty}(n+1)x^n$
必要ならば$0\lt x \lt 1$のとき
$\displaystyle \lim_{n\to\infty} nx^n=0$であることを
証明なしで使ってもよい。
(4)無限級数$\displaystyle \sum_{n=0}^{\infty} nQn$を$p$を用いて表せ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第2問〜ねじれの位置にある直線上の2点ずつでできる四面体の体積の最大最小

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
空間の点$(0,0,1)$を通り
$(1,-1,0)$を方向ベクトルとする
直線を$\ell$とし、点$(1,0,3)$を通り$(0,1,-2)$を
方向ベクトルとする直線を$m$とする。
(1)$P$を$\ell$上の点とし、$Q$を$m$上の点とする。
また直線$PQ$は直線$\ell$と直線$m$に垂線であるとする。
このとき$P$と$Q$の座標、
および線分$PQ$の長さを求めよ。
(2)$\ell$上に$2$点
$A=(t,-t,1),$
$B(2+t+\sin t,-2-t-\sin t,1)$
があり、$m$上に$2$点
$C=(1,t,3,-2t),$
$D=(1,2+t<\cos t,-1-2t-2\cos t)$
があるとする。ただし、$y$は実数とする。
四面体$ABCD$の体積を$V(t)$とする。
$V(0)$を求めよ。
(3)$t$が$t\geqq 0$を動くとき、
$V(t)$の最大値と最小値を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{2}$
空間の点$(0,0,1)$を通り
$(1,-1,0)$を方向ベクトルとする
直線を$\ell$とし、点$(1,0,3)$を通り$(0,1,-2)$を
方向ベクトルとする直線を$m$とする。
(1)$P$を$\ell$上の点とし、$Q$を$m$上の点とする。
また直線$PQ$は直線$\ell$と直線$m$に垂線であるとする。
このとき$P$と$Q$の座標、
および線分$PQ$の長さを求めよ。
(2)$\ell$上に$2$点
$A=(t,-t,1),$
$B(2+t+\sin t,-2-t-\sin t,1)$
があり、$m$上に$2$点
$C=(1,t,3,-2t),$
$D=(1,2+t<\cos t,-1-2t-2\cos t)$
があるとする。ただし、$y$は実数とする。
四面体$ABCD$の体積を$V(t)$とする。
$V(0)$を求めよ。
(3)$t$が$t\geqq 0$を動くとき、
$V(t)$の最大値と最小値を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜旧・東京工業大学、東京科学大学2025理系第1問〜逆関数の定積分

単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
この動画を見る
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
福田の数学〜東京工業大学2024年理系第4問〜表の出る確率が異なるコインを投げたときの表が奇数枚出る確率と極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1-$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1-$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
福田の数学〜東京工業大学2024年理系第2問〜関数方程式と曲線の長さ

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 実数全体を定義域にもつ微分可能な関数$f(t)$, $g(t)$が次の6つの条件を満たしているとする。
$f'(t)$=$-f(t)g(t)$, $g'(t)$=$\left\{f(t)\right\}^2$,
$f(t)$>0, $|g(t)|$<1, $f(0)$=1, $g(0)$=0
このとき $p(t)$=$\left\{f(t)\right\}^2$+$\left\{g(t)\right\}^2$, $q(t)$=$\log\frac{1+g(t)}{1-g(t)}$ とおく。
(1)$p'(t)$を求めよ。
(2)$q'(t)$は定数関数であることを示せ。
(3)$\displaystyle\lim_{t \to \infty}g(t)$を求めよ。
(4)$f(T)$=$g(T)$となる正の実数$T$に対して、媒介変数表示された平面曲線($x$,$y$)=($f(t)$,$g(t)$) (0≦$t$≦$T$)の長さを求めよ。
この動画を見る
$\Large\boxed{2}$ 実数全体を定義域にもつ微分可能な関数$f(t)$, $g(t)$が次の6つの条件を満たしているとする。
$f'(t)$=$-f(t)g(t)$, $g'(t)$=$\left\{f(t)\right\}^2$,
$f(t)$>0, $|g(t)|$<1, $f(0)$=1, $g(0)$=0
このとき $p(t)$=$\left\{f(t)\right\}^2$+$\left\{g(t)\right\}^2$, $q(t)$=$\log\frac{1+g(t)}{1-g(t)}$ とおく。
(1)$p'(t)$を求めよ。
(2)$q'(t)$は定数関数であることを示せ。
(3)$\displaystyle\lim_{t \to \infty}g(t)$を求めよ。
(4)$f(T)$=$g(T)$となる正の実数$T$に対して、媒介変数表示された平面曲線($x$,$y$)=($f(t)$,$g(t)$) (0≦$t$≦$T$)の長さを求めよ。
【高校数学】毎日積分54日目 実践編⑤回転体シリーズ~斜めで、切り取って、最短距離のフルコース~【難易度:★★★★★】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$xyz$空間内において、連立不等式
$\frac{x^2}{4}+y^2≦1 , |z|≦6$
により定まる領域を$V$とし、2点$(2,0,2),(-2,0,-2)$を通る直線を$l$とする。
(1)$|t|≦2\sqrt2$を満たす実数tに対し、点$P_t(\frac{t}{\sqrt{2}},0,\frac{t}{\sqrt{2}})$を通り$l$に重直な平面を$H_t$とする。また、実数$\theta$に対し、点$(2\cos\theta,\sin\theta,0)$を通り$z$軸に平行な直線を$L_{\theta}$とする。$L_{\theta}$と$H_t$との交点の$z$座標を$t$と$\theta$を用いて表せ。
(2) $l$を回転軸に持つ回転体で$V$に含まれるものを考える。このような回転体のうちで体積が最大となるものの体積を求めよ。
【東京工業大学 2018】
この動画を見る
$xyz$空間内において、連立不等式
$\frac{x^2}{4}+y^2≦1 , |z|≦6$
により定まる領域を$V$とし、2点$(2,0,2),(-2,0,-2)$を通る直線を$l$とする。
(1)$|t|≦2\sqrt2$を満たす実数tに対し、点$P_t(\frac{t}{\sqrt{2}},0,\frac{t}{\sqrt{2}})$を通り$l$に重直な平面を$H_t$とする。また、実数$\theta$に対し、点$(2\cos\theta,\sin\theta,0)$を通り$z$軸に平行な直線を$L_{\theta}$とする。$L_{\theta}$と$H_t$との交点の$z$座標を$t$と$\theta$を用いて表せ。
(2) $l$を回転軸に持つ回転体で$V$に含まれるものを考える。このような回転体のうちで体積が最大となるものの体積を求めよ。
【東京工業大学 2018】
【高校数学】毎日積分33日目【難易度:★★★★★】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
この動画を見る
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
大学入試問題#615「ラッキー問題?」 東京工業大学(1976) #積分方程式
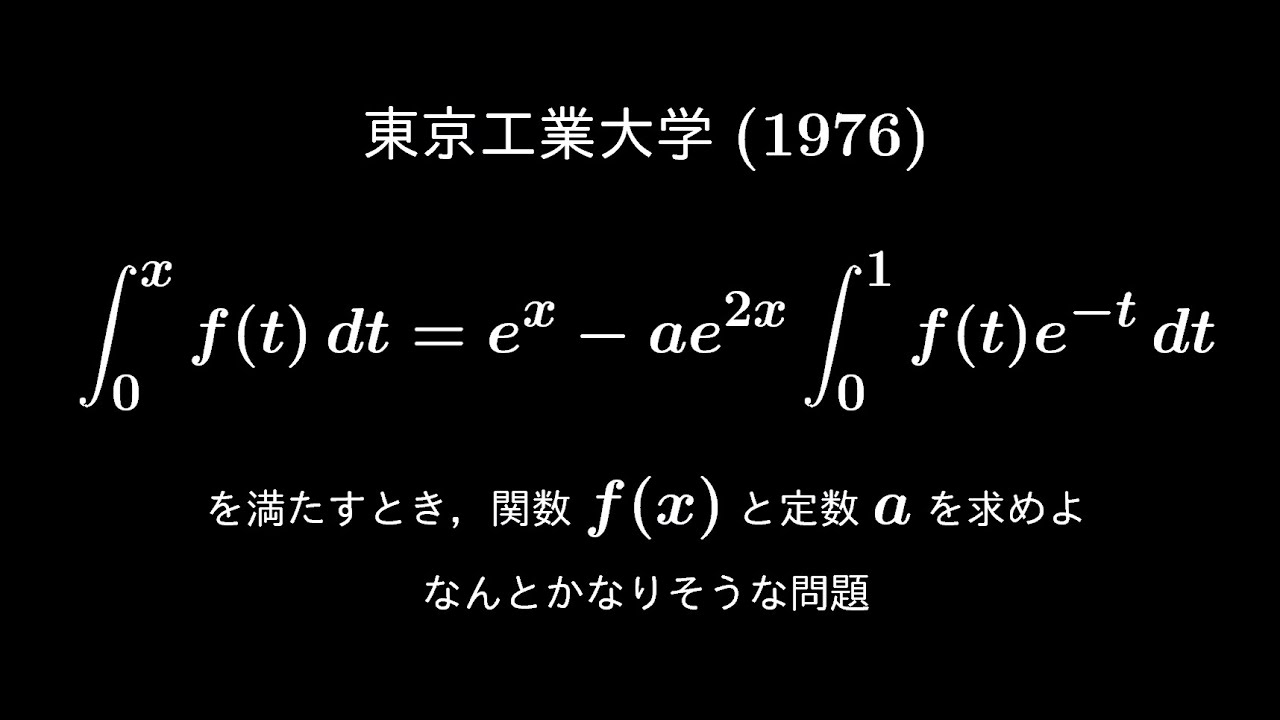
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{x} f(t)dt=e^x-ae^{2x}\displaystyle \int_{0}^{1} f(t)e^{-t}dt$のとき
関数$f(x),$定数$a$を求めよ。
出典:1976年東京工業大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{x} f(t)dt=e^x-ae^{2x}\displaystyle \int_{0}^{1} f(t)e^{-t}dt$のとき
関数$f(x),$定数$a$を求めよ。
出典:1976年東京工業大学 入試問題
福田の数学〜ChatGPTに東工大第1問を解かせてみたら大変なことに〜

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#その他#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\int_0^{2023}\frac{2}{x+e^x}dx$ の整数部分を求めよ。
東工大過去問
この動画を見る
$\displaystyle\int_0^{2023}\frac{2}{x+e^x}dx$ の整数部分を求めよ。
東工大過去問
2023年東工大の整数問題!86400!?大きい値をどう扱うか【東京工業大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$(x^3-x)^2(y^3-y)=86400$を満たす整数の組(x,y)を求めよ
東工大過去問
この動画を見る
$(x^3-x)^2(y^3-y)=86400$を満たす整数の組(x,y)を求めよ
東工大過去問
2023年東工大の整数問題!86400!?大きい値をどう扱うか【東京工業大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
方程式 $(x^{3}-x)^{2}(y^{3}-y)$=86400
を満たす整数の組$(x,y)$をすべて求めよ。
この動画を見る
方程式 $(x^{3}-x)^{2}(y^{3}-y)$=86400
を満たす整数の組$(x,y)$をすべて求めよ。
福田の数学〜東京工業大学2023年理系第5問(PART2)〜4直線に接する球面の決定

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
福田の数学〜東京工業大学2023年理系第5問(PART1)〜4直線に接する球面の決定

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#点と直線#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
福田の数学〜東京工業大学2023年理系第4問〜非回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ xyz空間においてx軸を軸とする半径2の円柱から、|y|<1かつ|z|<1で表される角柱の内部を取り除いたものをAとする。また、Aをx軸のまわりに45°回転してからz軸のまわりに90°回転したものをBとする。AとBの共通部分の体積を求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{4}$ xyz空間においてx軸を軸とする半径2の円柱から、|y|<1かつ|z|<1で表される角柱の内部を取り除いたものをAとする。また、Aをx軸のまわりに45°回転してからz軸のまわりに90°回転したものをBとする。AとBの共通部分の体積を求めよ。
2023東京工業大学理系過去問
福田の数学〜東京工業大学2023年理系第3問〜複素数の絶対値と偏角に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#漸化式#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 実数が書かれた3枚のカード$\boxed{0}$,$\boxed{1}$,$\boxed{\sqrt 3}$から無作為に2枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数nに対して、この操作をn回繰り返して得られるn個の複素数の積を$z_n$で表す。
(1)|$z_n$|<5となる確率$P_n$を求めよ。
(2)$z_n^2$が実数となる確率$Q_n$を求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{3}$ 実数が書かれた3枚のカード$\boxed{0}$,$\boxed{1}$,$\boxed{\sqrt 3}$から無作為に2枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数nに対して、この操作をn回繰り返して得られるn個の複素数の積を$z_n$で表す。
(1)|$z_n$|<5となる確率$P_n$を求めよ。
(2)$z_n^2$が実数となる確率$Q_n$を求めよ。
2023東京工業大学理系過去問
2023東工大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x^3-x)^2(y^3-y)=86400$
整数$x,y$を求めよ.
2023東工大過去問
この動画を見る
$(x^3-x)^2(y^3-y)=86400$
整数$x,y$を求めよ.
2023東工大過去問
福田の数学〜東京工業大学2023年理系第2問〜不定方程式の整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 方程式
$(x^3-x)^2$$(y^3-y)$=86400
を満たす整数の組(x,y)をすべて求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{2}$ 方程式
$(x^3-x)^2$$(y^3-y)$=86400
を満たす整数の組(x,y)をすべて求めよ。
2023東京工業大学理系過去問
福田の数学〜東京工業大学2023年理系第1問〜定積分の値の評価
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
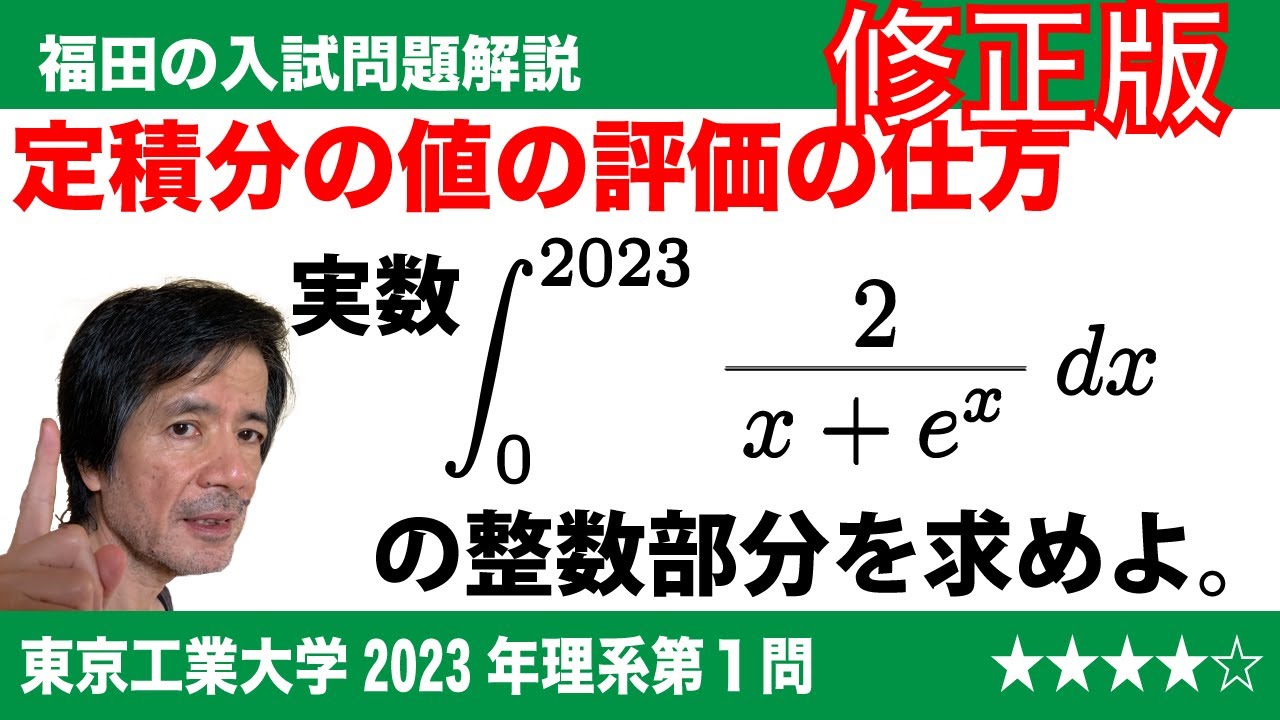
$\Large\boxed{1}$ 実数$\displaystyle\int_0^{2023}\frac{2}{x+e^x}dx$の整数部分を求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{1}$ 実数$\displaystyle\int_0^{2023}\frac{2}{x+e^x}dx$の整数部分を求めよ。
2023東京工業大学理系過去問
福田の数学〜東京工業大学2023年理系第1問〜定積分の値の評価

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 実数$\displaystyle\int_0^{2023}\frac{2}{x+e^x}dx$の整数部分を求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{1}$ 実数$\displaystyle\int_0^{2023}\frac{2}{x+e^x}dx$の整数部分を求めよ。
2023東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題089〜東京工業大学2018年度理系第2問〜3変数の不定方程式の整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 次の問いに答えよ。
(1)35x+91y+65z=3 を満たす整数の組(x,y,z)を一組求めよ。
(2)35x+91y+65z=3 を満たす整数の組(x,y,z)の中で$x^2+y^2$の値が最小となるもの、およびその最小値を求めよ。
2018東京工業大学理系過去問
この動画を見る
$\Large\boxed{2}$ 次の問いに答えよ。
(1)35x+91y+65z=3 を満たす整数の組(x,y,z)を一組求めよ。
(2)35x+91y+65z=3 を満たす整数の組(x,y,z)の中で$x^2+y^2$の値が最小となるもの、およびその最小値を求めよ。
2018東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題020〜東京工業大学2016年度理系数学第5問〜媒介変数で表された曲線の追跡と面積

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東京工業大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
次のように媒介変数表示されたxy平面上の曲線をCとする。
$\left\{\begin{array}{1}
x=3\cos t-\cos3t
y=3\sin t-\sin3t
\end{array}\right.$
ただし、$0 \leqq t \leqq \frac{\pi}{2}$である。
(1)$\frac{dx}{dt}$および$\frac{dy}{dt}$を計算し、Cの概形を図示せよ。
(2)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2016東京工業大学理系過去問
この動画を見る
次のように媒介変数表示されたxy平面上の曲線をCとする。
$\left\{\begin{array}{1}
x=3\cos t-\cos3t
y=3\sin t-\sin3t
\end{array}\right.$
ただし、$0 \leqq t \leqq \frac{\pi}{2}$である。
(1)$\frac{dx}{dt}$および$\frac{dy}{dt}$を計算し、Cの概形を図示せよ。
(2)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2016東京工業大学理系過去問
福田の1.5倍速演習〜合格する重要問題019〜東京工業大学2016年度理系数学第4問〜整数に関する論証

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを2以上の自然数とする。
(1)nが素数または4のとき、$(n-1)!$はnで割り切れないことを示せ。
(2)nが素数でなくかつ4でもないとき、$(n-1)!$はnで割り切れることを示せ。
2016東京工業大学理系過去問
この動画を見る
nを2以上の自然数とする。
(1)nが素数または4のとき、$(n-1)!$はnで割り切れないことを示せ。
(2)nが素数でなくかつ4でもないとき、$(n-1)!$はnで割り切れることを示せ。
2016東京工業大学理系過去問
福田の数学〜東京工業大学2022年理系第5問〜定積分と不等式と区分求積

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
この動画を見る
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
福田の数学〜東京工業大学2022年理系第4問〜複素数平面上の点の軌跡と線分の通過範囲

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
aを正の実数とする。複素数$z$が$|z-1|=a$かつ$z\neq \frac{1}{2}$を満たしながら
動くとき、複素数平面上の点$w=\frac{z-3}{1-2z}$が描く図形をKとする。
このとき、次の問いに答えよ。
(1)Kが円となるためのaの条件を求めよ。また、そのとき
Kの中心が表す複素数とKの半径を、それぞれaを用いて表せ。
(2)aが(1)の条件を満たしながら動くとき、虚軸に平行で円Kの直径となる
線分が通過する領域を複素数平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
aを正の実数とする。複素数$z$が$|z-1|=a$かつ$z\neq \frac{1}{2}$を満たしながら
動くとき、複素数平面上の点$w=\frac{z-3}{1-2z}$が描く図形をKとする。
このとき、次の問いに答えよ。
(1)Kが円となるためのaの条件を求めよ。また、そのとき
Kの中心が表す複素数とKの半径を、それぞれaを用いて表せ。
(2)aが(1)の条件を満たしながら動くとき、虚軸に平行で円Kの直径となる
線分が通過する領域を複素数平面上に図示せよ。
2022東京工業大学理系過去問
福田の数学〜東京工業大学2022年理系第3問〜直角三角形の頂点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\alphaは0 \lt \alpha \lt \frac{\pi}{2}$を満たす実数とする。
$\angle A=\alpha$および$\angle P=\frac{\pi}{2}$を満たす直角三角形APB
が、次の2つの条件$(\textrm{a}),(\textrm{b})$を満たしながら、時刻t=0から時刻$t=\frac{\pi}{2}$まで
xy平面上を動くとする。
$(\textrm{a})$時刻tでの点A,Bの座標は、それぞれ$A(\sin t,0),B(0, \cos t)$である。
$(\textrm{b})$点Pは第一象限内にある。
このとき、次の問いに答えよ。
(1)点Pはある直線上を動くことを示し、その直線の方程式を$\alpha$を用いて表せ。
(2)時刻$t=0$から時刻$t=\frac{\pi}{2}$までの間に点Pが動く道のりを$\alpha$を用いて表せ。
(3)xy平面内において、連立不等式
$x^2-x+y^2 \lt 0, x^2+y^2-y \lt 0$
により定まる領域をDとする。このとき、点Pは領域Dには入らないことを示せ。
2022東京工業大学理系過去問
この動画を見る
$\alphaは0 \lt \alpha \lt \frac{\pi}{2}$を満たす実数とする。
$\angle A=\alpha$および$\angle P=\frac{\pi}{2}$を満たす直角三角形APB
が、次の2つの条件$(\textrm{a}),(\textrm{b})$を満たしながら、時刻t=0から時刻$t=\frac{\pi}{2}$まで
xy平面上を動くとする。
$(\textrm{a})$時刻tでの点A,Bの座標は、それぞれ$A(\sin t,0),B(0, \cos t)$である。
$(\textrm{b})$点Pは第一象限内にある。
このとき、次の問いに答えよ。
(1)点Pはある直線上を動くことを示し、その直線の方程式を$\alpha$を用いて表せ。
(2)時刻$t=0$から時刻$t=\frac{\pi}{2}$までの間に点Pが動く道のりを$\alpha$を用いて表せ。
(3)xy平面内において、連立不等式
$x^2-x+y^2 \lt 0, x^2+y^2-y \lt 0$
により定まる領域をDとする。このとき、点Pは領域Dには入らないことを示せ。
2022東京工業大学理系過去問
福田の数学〜東工大2022理系1修正版

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
福田の数学〜東京工業大学2022年理系第2問〜3つの数の最大公約数

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
この動画を見る
3つの正の整数a,b,cの最大公約数が1であるとき、次の問いに答えよ。
(1)$a+b+c,ab+bc+ca,abc$の最大公約数は1であることを示せ。
(2)$a+b+c,a^2+b^2+c^2,a^3+b^3+c^3$の最大公約数となるような正の整数を
全て求めよ。
2022東京工業大学理系過去問
福田の数学〜東京工業大学2022年理系第1問〜2次方程式の解の存在範囲

単元:
#大学入試過去問(数学)#2次関数#複素数平面#2次方程式と2次不等式#図形への応用#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
a,bを実数とし、$f(z)=z^2+az+b$ とする。a,bが
$|a| \leqq 1, |b| \leqq 1$
を満たしながら動くとき、$f(z)=0$を満たす複素数zが取りうる値の範囲を
複素平面上に図示せよ。
2022東京工業大学理系過去問
