 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
福田の数学〜東京理科大学2024創域理工学部第1問(3)〜条件を満たす点の個数

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は?また、$b=\sqrt{3}$のとき、$U$の要素の個数は?
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は?また、$b=2\sqrt2$のとき、$U$の要素の個数は?
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は?また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は?
この動画を見る
$a,b$を正の実数とする。座標平面上に点$\textrm{A}(a,1)$をとり、自然数$n=1,2,3,\cdots$に対して点$\textrm{P}_n(n,0)$をとる。集合$U$を次で定める。
$U=\{n|n$は自然数かつ2点$\textrm{A}, \textrm{P}_n$間の距離は$b$以下$\}$
(a) $a=2$とする。$b=1$のとき、$U$の要素の個数は?また、$b=\sqrt{3}$のとき、$U$の要素の個数は?
(b) $a=\dfrac72$とする。$b=\sqrt2$のとき、$U$の要素の個数は?また、$b=2\sqrt2$のとき、$U$の要素の個数は?
(c) $b=2$のとき、$U$の要素の個数が2個となる正の整数$a$は?また、$b=5$のとき、$U$の要素の個数が9個となる最小の正の整数$a$は?
【数学】2023年度 第3回 高2模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1:小問集合
(1)実数xの2次方程式$2x^2-3x+1<0$を解け。
(2)$(3x+y)^4$を展開したときの$x^2y^2$の係数を答えよ。
(3)5つの文字A,B,C,D,Eを円形に並べる方法は何通りか。
(4)次のデータの平均値は3であるとする。1,2,3,7,a。aの値を求めよ。また、このデータの分散を求めよ。
(5)mは実数の定数とする。xy平面上の2直線$l_1:3x-y+5=0,l_2:mx+2y+4=0$が垂直になるとき、mの値を求めよ。
(6)実数xの方程式$4^x=2\sqrt{2}$を解け。
(7)実数x,yについて、x>0かつy>0であることは、xy>0であるための何条件か?
(選択肢)①必要十分条件である。②必要条件であるが、十分条件ではない。③十分条件であるが、必要条件ではない。④必要条件でも、十分条件でもない
大問2-1:高次方程式
a,bを実数の定数とする。xの3次式$P(x)=x^3+(2a-1)x^2-(a^2+2a-2)x+b$があり、3次方程式 P(x)=0がx=1を解にもつ。
(1)bをaを用いて表せ。
(2)P(x)を1次式x−1で割ったときの商をaを用いて表せ。
(3)3次方程式P(x)=0において、異なる実数解の個数が2となるようなaの値を求めよ。
大問2-2:確率
赤球1個と白球1個と青球1個の合計3個の球が入った袋がある。この袋から 1個の球を取り出しその色を確認して袋に戻すことを、繰り返し5回行う。
(1)5回とも赤球が取り出される確率を求めよ。
(2)5回のうち、赤球が2回取り出され、かつ白球が3回取り出される確率を求めよ。
(3)3種類の色の球が取り出される確率を求めよ。
大問3:図形と方程式
mを実数の定数とする。Oを原点とするxy平面上に点(2,3)を通り、傾きがmの直線がある。また、2点A(1,0),B(-1,0)があり、軸上のy>0の部分にある点Cが∠ACB=90°を満たしている。
(1)lの方程式を求めよ。また、Cの座標を求めよ。
(2)点Cと直線の距離をdとする。dをmを用いて表せ。
(3)不等式y>0の表す領域内の点Pが∠APB=45°を満たして動くとき、Pが描く図形をKとする。
(i)Kはある円の一部である。その円の中心の座標と半径を求めよ。
(ii)aを正の定数とし、Kと線分AB (両端を含む)で囲まれる領域(境界を含む)をDとする。点(x,y)がD上を動くとき、$\displaystyle\frac{y-a}{x-2}$の最大値をM(a)とする。M($\frac{1}{2}$)とM(3)をそれぞれ求めよ。
大問4:三角関数
kはk≧1を満たす定数とする。下の図のように、OB=1,∠OAB=$\frac{π}{2}$,∠AOB=θ(0<θ<$\frac{π}{4}$)である直角三角形OABがある。また、半直線OA上に点Pを、OP=2kABを満たすようにとる。
(1)辺OAの長さをを用いて表せ。また、線分OPの長さをk、θを用いて表せ。
(2)sinθcosθをsin2θを用いて表せ。また、sin²θをcos2θを用いて表せ。
(3) $BP^2$をk, sin2θ,cos2θを用いて表せ。
(4-i) k=1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$の最小値を求めよ。また、そのときのθの値を求めよ。
(4-ii) k>1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$のとり得る値の範囲をkを用いて表せ。
大問5:微分法
3次関数 $f(x)=x^3+kx^2-kx+k^2$がある。ただし、kは実数とする。
(1)f'(−1)=0とする。
(i)kの値を求めよ。
(ii)0≦x≦1におけるf(x)の最大値と最小値を求めよ。
(2)f(x)はx>0の範囲に極大値と極小値をもつとする。
(i)kのとり得る値の範囲を求めよ。
(ii)f(x)の極大値と極小値の和をS(k)とする。kの値が(2-i)で求めた範囲を変化するとき、S(k)の最大値を求めよ。
大問6:数列
数列{$a_n$}を$a_1=\frac{1}{\sqrt{2}},a_2=\sqrt{2},a_{n+2}a_{n+1}-a_{n+1}a_{n}=n+1(n=1,2,3,...)$により定める。また、数列{$b_n$}を$b_n=a_{n+1}a_{n}(n=1,2,3,・・・)$により定める。
(1)$b_1$を求めよ。また、$b_{n+1}$を$b_n$を用いて表せ。
(2)数列{$b_n$}の一般項を求めよ。
(3)$c_n=\displaystyle\frac{\sqrt{2}a_n}{n}(n=1,2,3,…)$とおく。$c_{n+1}$を$c_n$を用いて表せ。また、数列{$c_n$}の一般項を求めよ。
(4)$a_n>50$を満たす最小の正の整数の値をNとするとき、$\displaystyle \sum_{k=1}^N\frac{2k+1}{{a_{n+1}}^2{a_n}²}$を求めよ。
この動画を見る
大問1:小問集合
(1)実数xの2次方程式$2x^2-3x+1<0$を解け。
(2)$(3x+y)^4$を展開したときの$x^2y^2$の係数を答えよ。
(3)5つの文字A,B,C,D,Eを円形に並べる方法は何通りか。
(4)次のデータの平均値は3であるとする。1,2,3,7,a。aの値を求めよ。また、このデータの分散を求めよ。
(5)mは実数の定数とする。xy平面上の2直線$l_1:3x-y+5=0,l_2:mx+2y+4=0$が垂直になるとき、mの値を求めよ。
(6)実数xの方程式$4^x=2\sqrt{2}$を解け。
(7)実数x,yについて、x>0かつy>0であることは、xy>0であるための何条件か?
(選択肢)①必要十分条件である。②必要条件であるが、十分条件ではない。③十分条件であるが、必要条件ではない。④必要条件でも、十分条件でもない
大問2-1:高次方程式
a,bを実数の定数とする。xの3次式$P(x)=x^3+(2a-1)x^2-(a^2+2a-2)x+b$があり、3次方程式 P(x)=0がx=1を解にもつ。
(1)bをaを用いて表せ。
(2)P(x)を1次式x−1で割ったときの商をaを用いて表せ。
(3)3次方程式P(x)=0において、異なる実数解の個数が2となるようなaの値を求めよ。
大問2-2:確率
赤球1個と白球1個と青球1個の合計3個の球が入った袋がある。この袋から 1個の球を取り出しその色を確認して袋に戻すことを、繰り返し5回行う。
(1)5回とも赤球が取り出される確率を求めよ。
(2)5回のうち、赤球が2回取り出され、かつ白球が3回取り出される確率を求めよ。
(3)3種類の色の球が取り出される確率を求めよ。
大問3:図形と方程式
mを実数の定数とする。Oを原点とするxy平面上に点(2,3)を通り、傾きがmの直線がある。また、2点A(1,0),B(-1,0)があり、軸上のy>0の部分にある点Cが∠ACB=90°を満たしている。
(1)lの方程式を求めよ。また、Cの座標を求めよ。
(2)点Cと直線の距離をdとする。dをmを用いて表せ。
(3)不等式y>0の表す領域内の点Pが∠APB=45°を満たして動くとき、Pが描く図形をKとする。
(i)Kはある円の一部である。その円の中心の座標と半径を求めよ。
(ii)aを正の定数とし、Kと線分AB (両端を含む)で囲まれる領域(境界を含む)をDとする。点(x,y)がD上を動くとき、$\displaystyle\frac{y-a}{x-2}$の最大値をM(a)とする。M($\frac{1}{2}$)とM(3)をそれぞれ求めよ。
大問4:三角関数
kはk≧1を満たす定数とする。下の図のように、OB=1,∠OAB=$\frac{π}{2}$,∠AOB=θ(0<θ<$\frac{π}{4}$)である直角三角形OABがある。また、半直線OA上に点Pを、OP=2kABを満たすようにとる。
(1)辺OAの長さをを用いて表せ。また、線分OPの長さをk、θを用いて表せ。
(2)sinθcosθをsin2θを用いて表せ。また、sin²θをcos2θを用いて表せ。
(3) $BP^2$をk, sin2θ,cos2θを用いて表せ。
(4-i) k=1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$の最小値を求めよ。また、そのときのθの値を求めよ。
(4-ii) k>1とする。θが0<θ<$\frac{π}{4}$の範囲を変化するとき、$BP^2$のとり得る値の範囲をkを用いて表せ。
大問5:微分法
3次関数 $f(x)=x^3+kx^2-kx+k^2$がある。ただし、kは実数とする。
(1)f'(−1)=0とする。
(i)kの値を求めよ。
(ii)0≦x≦1におけるf(x)の最大値と最小値を求めよ。
(2)f(x)はx>0の範囲に極大値と極小値をもつとする。
(i)kのとり得る値の範囲を求めよ。
(ii)f(x)の極大値と極小値の和をS(k)とする。kの値が(2-i)で求めた範囲を変化するとき、S(k)の最大値を求めよ。
大問6:数列
数列{$a_n$}を$a_1=\frac{1}{\sqrt{2}},a_2=\sqrt{2},a_{n+2}a_{n+1}-a_{n+1}a_{n}=n+1(n=1,2,3,...)$により定める。また、数列{$b_n$}を$b_n=a_{n+1}a_{n}(n=1,2,3,・・・)$により定める。
(1)$b_1$を求めよ。また、$b_{n+1}$を$b_n$を用いて表せ。
(2)数列{$b_n$}の一般項を求めよ。
(3)$c_n=\displaystyle\frac{\sqrt{2}a_n}{n}(n=1,2,3,…)$とおく。$c_{n+1}$を$c_n$を用いて表せ。また、数列{$c_n$}の一般項を求めよ。
(4)$a_n>50$を満たす最小の正の整数の値をNとするとき、$\displaystyle \sum_{k=1}^N\frac{2k+1}{{a_{n+1}}^2{a_n}²}$を求めよ。
#北海道大学1957#因数分解_64

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
この動画を見る
$2x^2-xy-y^2-7x+y+6$を因数分解せよ.
1957北海道大学過去問題
福田の数学〜東京理科大学2024創域理工学部第1問(2)〜三角不等式の解法

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
この動画を見る
$\boxed{1}(2)0 \leqq θ \lt 2π$のとき、次の不等式を解こう。
$sin2θ \gt 2cos(θ+\frac{π}{6})+\frac{\sqrt{3}}{2}・・・③$
$a=cosθ,b=sinθ$とおくと、次の不等式$③$は
$\boxed{キ}ab-\boxed{ク}\sqrt{\boxed{ケ}}a+\boxed{コ}b-\sqrt{2}\gt0 ・・・④$
となる。不等式$④$の左辺は
$(\boxed{サ}a+\boxed{シ})(\boxed{ス}b-\sqrt{セ})$
と因数分解できる。これより、不等式$③$の解は
$\frac{π}{\boxed{ソ}} \lt θ \lt \frac{\boxed{タ}}{\boxed{チ}}π$または$\frac{\boxed{ツ}}{\boxed{テ}}π \lt θ \lt\frac{\boxed{ト}}{\boxed{ナ}}π$
と求まる。
福田の数学〜東京理科大学2024創域理工学部第1問(1)〜複素数と三角形の外接円

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
この動画を見る
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
福田の数学〜上智大学2024理工学部第3問〜円の内部を反射しながら進む点の通過範囲

単元:
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
点$O$を中心とし半径が$1$の円形のビリヤード台がある。台の縁の点$P_1$に大きさが無視できる球$Q$を置き、半径$P_1O$とのなす角が$\frac{\pi}{8}$の方向へ球$Q$を打ち出す。
球$Q$は、ビリヤード台の縁に当たると、図のように入射角と反射角が等しくなるように反射し、一度打ち出されたら止まらないものとする。
$i=1,2,3,\cdots$に対し、点$P_i$の次に球$Q$が縁に当たる点を$P_{i+1}$とし、$\overrightarrow{OP_i}=\overrightarrow{p_i}$とする。
(1)$\overrightarrow{p_3}=\fbox{あ}\overrightarrow{p_1}+\fbox{い}\overrightarrow{p_2},\overrightarrow{p_4}=\fbox{う}\overrightarrow{p_1}+\fbox{え}\overrightarrow{p_2}$である。
(2)$P_i=P_1となるiのうち、 i\geqq 2で最小のものは\fbox{ソ}である。$
(3)$線分P_1P_2とP_3P_4 との交点をA、線分P_1P_2とP_6P_7との交点をBとすると$
$\overrightarrow{OA}=\fbox{お}\overrightarrow{p_1}+\fbox{か}\overrightarrow{p_2},\overrightarrow{OB}=\fbox{き}\overrightarrow{p_1}+\fbox{く}\overrightarrow{p_2}$である。
(4)球$Q$が点$P_1$から打ち出されてから初めて再び点$P_1$に到達するまでに、中心$O$と球$Q$とを結ぶ線分$OQ$がちょうど2回通過する領域の面積は$\fbox{タ}+\fbox{チ}\sqrt{2}$である。
この動画を見る
点$O$を中心とし半径が$1$の円形のビリヤード台がある。台の縁の点$P_1$に大きさが無視できる球$Q$を置き、半径$P_1O$とのなす角が$\frac{\pi}{8}$の方向へ球$Q$を打ち出す。
球$Q$は、ビリヤード台の縁に当たると、図のように入射角と反射角が等しくなるように反射し、一度打ち出されたら止まらないものとする。
$i=1,2,3,\cdots$に対し、点$P_i$の次に球$Q$が縁に当たる点を$P_{i+1}$とし、$\overrightarrow{OP_i}=\overrightarrow{p_i}$とする。
(1)$\overrightarrow{p_3}=\fbox{あ}\overrightarrow{p_1}+\fbox{い}\overrightarrow{p_2},\overrightarrow{p_4}=\fbox{う}\overrightarrow{p_1}+\fbox{え}\overrightarrow{p_2}$である。
(2)$P_i=P_1となるiのうち、 i\geqq 2で最小のものは\fbox{ソ}である。$
(3)$線分P_1P_2とP_3P_4 との交点をA、線分P_1P_2とP_6P_7との交点をBとすると$
$\overrightarrow{OA}=\fbox{お}\overrightarrow{p_1}+\fbox{か}\overrightarrow{p_2},\overrightarrow{OB}=\fbox{き}\overrightarrow{p_1}+\fbox{く}\overrightarrow{p_2}$である。
(4)球$Q$が点$P_1$から打ち出されてから初めて再び点$P_1$に到達するまでに、中心$O$と球$Q$とを結ぶ線分$OQ$がちょうど2回通過する領域の面積は$\fbox{タ}+\fbox{チ}\sqrt{2}$である。
福田の数学〜上智大学2024理工学部第1問(3)〜回路に電流が流れて電球が点灯する確率の最大
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
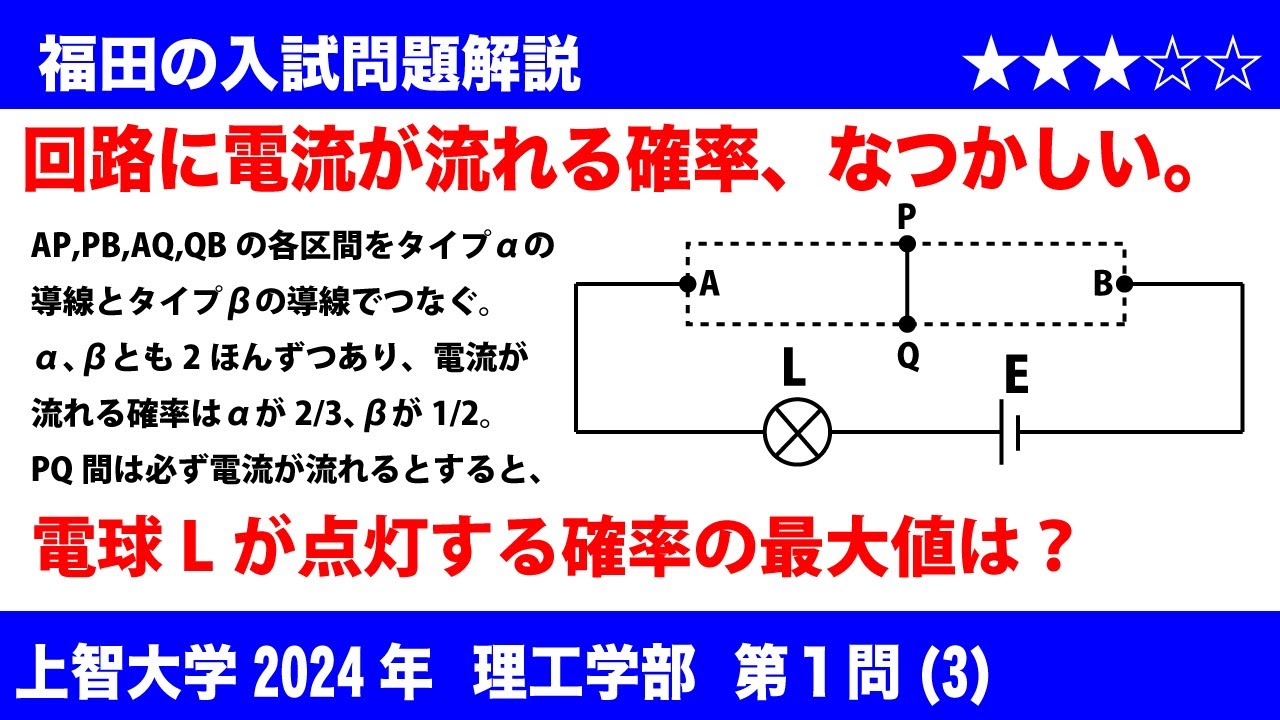
次の図で表される回路は、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間がつながっておらず、それぞれの区間を1本の導線でつなぐことができる。$\rm P$または$\rm Q$を経由して$\rm AB$間がつながり電流が流れると電球が点灯する。導線にはタイプαが2本、タイプβが2本ある。それぞれの導線に電流が流れる確率はタイプαが$\dfrac23$、タイプβが$\dfrac12$である。
(i) $\rm AP$間、$\rm PB$間を2本のタイプαの導線でそれぞれつなぐとき、$\rm L$が点灯する確率は?
(ii) $\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
(iii) $\rm PQ$間を確実に電流が流れる別の導線でつなぎ、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間を4本の導線でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
この動画を見る
次の図で表される回路は、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間がつながっておらず、それぞれの区間を1本の導線でつなぐことができる。$\rm P$または$\rm Q$を経由して$\rm AB$間がつながり電流が流れると電球が点灯する。導線にはタイプαが2本、タイプβが2本ある。それぞれの導線に電流が流れる確率はタイプαが$\dfrac23$、タイプβが$\dfrac12$である。
(i) $\rm AP$間、$\rm PB$間を2本のタイプαの導線でそれぞれつなぐとき、$\rm L$が点灯する確率は?
(ii) $\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
(iii) $\rm PQ$間を確実に電流が流れる別の導線でつなぎ、$\rm AP$間、$\rm AQ$間、$\rm PB$間、$\rm QB$間を4本の導線でそれぞれつなぐすべてのパターンを考える。$\rm L$が点灯する確率が最も大きくなるときの確率は?
福田の数学〜上智大学2024理工学部第1問(2)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{2\sin x}{x^3}dx=-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{\sin x}{x}dx+\fbox{エ}\pi^p+\fbox{オ}\sqrt{\fbox{カ}}\pi^q$
ただし、$p=\fbox{キ},q=\fbox{ク}$である。
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{2\sin x}{x^3}dx=-\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}\dfrac{\sin x}{x}dx+\fbox{エ}\pi^p+\fbox{オ}\sqrt{\fbox{カ}}\pi^q$
ただし、$p=\fbox{キ},q=\fbox{ク}$である。
#北海道大学1919#因数分解_63

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
この動画を見る
$a^4+b^4+c^4-2b^2c^2-2c^2a^2-2a^2b^2$を因数分解せよ.
1919北海道帝国大学過去問題
5つの文字を求めよ!?東大の整数問題【東京大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この動画を見る
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
大学入試問題#869「次数は分子の方が高いのね」 #玉川大学(2022) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
問題文全文(内容文):
$\displaystyle \frac{12n^2+13n+51}{3n+1}$が整数となるような整数$n$をすべて求めよ。
出典:2022年玉川大学 入試問題
この動画を見る
$\displaystyle \frac{12n^2+13n+51}{3n+1}$が整数となるような整数$n$をすべて求めよ。
出典:2022年玉川大学 入試問題
福田の数学〜上智大学2024TEAP利用型理系第1問(3)〜対数不等式を満たす最小の整数

単元:
#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
この動画を見る
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
福田の数学〜上智大学2024TEAP利用型理系第1問(1)〜不定方程式の解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)77x+52y=1$を満たす整数$x$、$y$の組のうち、$x$が正で最小の組は$(x,y)=(\boxed{ア},\boxed{イ})$である。
この動画を見る
$\boxed{1}(1)77x+52y=1$を満たす整数$x$、$y$の組のうち、$x$が正で最小の組は$(x,y)=(\boxed{ア},\boxed{イ})$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(4)〜線分の通過範囲の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#軌跡と領域#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
この動画を見る
$\boxed{2}(4)$座標平面上で放物線$y=x^2$上の点P$(t,t^2)(0 \leqq t \leqq 1)$における接線$y=-(x+1)^2$の二つの共有点の中点をQとする。ただし、共有点が1つの場合は、その共有点をQとする。Qの座標は$(\boxed{ユ}t+\boxed{ヨ}
,\boxed{ラ}t^2+\boxed{リ}t+\boxed{ル})$である。
tが$0 \leqq t \leqq1$の範囲を動くとき線分PQが動いてできる図形の面積は$\frac{\boxed{レ}}{\boxed{ロ}}$である
2024年度第2回記述模試高3数学解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
問題文全文(内容文):
大問1
(1) 袋の中に5枚のコインが入っており、そのうち2枚には両面にAが書かれており、残り3枚には片面にA、もう一方の面にBが書かれている。
(ⅰ)袋から無作為にコインを1枚選び、選んだコインを投げたとき、Aが書かれた面が上になる確率を求めよ。
(ⅱ)袋から無作為にコインを1枚選び、選んだコインを投げたとき、Aが書かれた面が上になった。このとき、下の面にもAが書かれている確率を求めよ。
(2) 多項式$(x-1)^{99}$を$x^2$で割った時の余りを求めよ。また、整数$99^{99}$を10000で割った時の余りを求めよ。
(3) $12^{12}$の桁数を求めよ。
(4)$\displaystyle z=\frac{-\sqrt{3}+i}{1+i}$とする。
(ⅰ)zを極形式で表せ。
(ⅱ)nを正の整数とする。$z^n$が実数となるような最小のnを求めよ。
大問2
数列${a_n}$の初項$a_1$から第n項$a_n$までの和を$S_n$、数列${b_n}$の初項$b_1$から第n項$b_n$までの和を$T_n$をとするとき
$a_1=2、b_1=0、a_{n+1}=2T_n+2、b_{n+1}=2S_n$ が成り立つ。
(1) $a_2、b_2$を求めよ
(2) $a_{n+1}、b_{n+1}$を$a_n、b_n$を用いて表せ。
(3) 一般項$a_n$を求めよ。
大問3
aは実数の定数とし、関数f(x)を
$f(x)=e^{-x}(a-sinx-cosx) (0<x<2π)$により定める。
(1)f(x)が極値を持つとき、aの値の範囲を求めよ。
(2)f(x)が極値を2つ持つときを考える。極値の積が負となるとき、aの値の範囲を求めよ。また、極値の積が$\displaystyle \frac{-e^{-3π}}{2}$となるときのaの値を全て求めよ。
大問4
AB=1、AC=3、BC=$2\sqrt{3}$である三角形ABCがある。$\overrightarrow{AB}=\vec{b}、\overrightarrow{AC}=\vec{c}$とする。
(1) 内積$\vec{b}・\vec{c}$の値を求めよ。
(2) s,tを実数とし、$\overrightarrow{AP}=s\vec{b}+t\vec{c}$とする。AB⊥BP、AC⊥CPであるとき、s,tの値を求め、さらに|$\overrightarrow{AP}$|を求めよ。
(3)点Qが三角形ABCの外接円上を動くとき、三角形BCQの面積を最大にするQを$Q_0$とする。$\overrightarrow{AQ_0}$を$\vec{b},\vec{c}$を用いて表せ。
大問5
$0≦x<π$において定義された関数
$f(x)=\displaystyle \frac{2sinx}{1+cosx}、g(x)=\frac{\sqrt{3}}{1+cosx}$
があり、曲線y=f(x)を$C_1$、曲線y=g(x)を$C_2$とする。
(1) $C_1、C_2$の共有点のx座標を求めよ
(2)(ⅰ)不定積分$\int f(x)dx$を求めよ
(ⅱ)$tan\frac{2}{x}$の導関数をcosxを用いて表せ
(3)$C_1、C_2$およびy軸の3つで囲まれる部分の面積を$S_1$とし、$C_1$と$C_2$で囲まれる部分の面積を$S_2$とする。$S_1$と$S_2$の大小を比較せよ。ただし、自然対数の底eについて、2.7<e<2.8であることは用いてよい。
大問6
正の整数Nを3で割った時の余りは2である。
(1)正の整数a,bを3で割った時の余りをそれぞれ$r_a、r_b$とする。ab=Nが成り立つとき、$r_a、r_b$の組をすべて求めよ。
(2)Nの正の約数の総和を3で割った時の余りを求めよ。
(3)Nの正の約数の逆数の総和を$\displaystyle \frac{q}{p}$(ただし、pとqはともに正の整数で最大公約数は1である)と表したとき、qは3の倍数であることを示せ。
この動画を見る
大問1
(1) 袋の中に5枚のコインが入っており、そのうち2枚には両面にAが書かれており、残り3枚には片面にA、もう一方の面にBが書かれている。
(ⅰ)袋から無作為にコインを1枚選び、選んだコインを投げたとき、Aが書かれた面が上になる確率を求めよ。
(ⅱ)袋から無作為にコインを1枚選び、選んだコインを投げたとき、Aが書かれた面が上になった。このとき、下の面にもAが書かれている確率を求めよ。
(2) 多項式$(x-1)^{99}$を$x^2$で割った時の余りを求めよ。また、整数$99^{99}$を10000で割った時の余りを求めよ。
(3) $12^{12}$の桁数を求めよ。
(4)$\displaystyle z=\frac{-\sqrt{3}+i}{1+i}$とする。
(ⅰ)zを極形式で表せ。
(ⅱ)nを正の整数とする。$z^n$が実数となるような最小のnを求めよ。
大問2
数列${a_n}$の初項$a_1$から第n項$a_n$までの和を$S_n$、数列${b_n}$の初項$b_1$から第n項$b_n$までの和を$T_n$をとするとき
$a_1=2、b_1=0、a_{n+1}=2T_n+2、b_{n+1}=2S_n$ が成り立つ。
(1) $a_2、b_2$を求めよ
(2) $a_{n+1}、b_{n+1}$を$a_n、b_n$を用いて表せ。
(3) 一般項$a_n$を求めよ。
大問3
aは実数の定数とし、関数f(x)を
$f(x)=e^{-x}(a-sinx-cosx) (0<x<2π)$により定める。
(1)f(x)が極値を持つとき、aの値の範囲を求めよ。
(2)f(x)が極値を2つ持つときを考える。極値の積が負となるとき、aの値の範囲を求めよ。また、極値の積が$\displaystyle \frac{-e^{-3π}}{2}$となるときのaの値を全て求めよ。
大問4
AB=1、AC=3、BC=$2\sqrt{3}$である三角形ABCがある。$\overrightarrow{AB}=\vec{b}、\overrightarrow{AC}=\vec{c}$とする。
(1) 内積$\vec{b}・\vec{c}$の値を求めよ。
(2) s,tを実数とし、$\overrightarrow{AP}=s\vec{b}+t\vec{c}$とする。AB⊥BP、AC⊥CPであるとき、s,tの値を求め、さらに|$\overrightarrow{AP}$|を求めよ。
(3)点Qが三角形ABCの外接円上を動くとき、三角形BCQの面積を最大にするQを$Q_0$とする。$\overrightarrow{AQ_0}$を$\vec{b},\vec{c}$を用いて表せ。
大問5
$0≦x<π$において定義された関数
$f(x)=\displaystyle \frac{2sinx}{1+cosx}、g(x)=\frac{\sqrt{3}}{1+cosx}$
があり、曲線y=f(x)を$C_1$、曲線y=g(x)を$C_2$とする。
(1) $C_1、C_2$の共有点のx座標を求めよ
(2)(ⅰ)不定積分$\int f(x)dx$を求めよ
(ⅱ)$tan\frac{2}{x}$の導関数をcosxを用いて表せ
(3)$C_1、C_2$およびy軸の3つで囲まれる部分の面積を$S_1$とし、$C_1$と$C_2$で囲まれる部分の面積を$S_2$とする。$S_1$と$S_2$の大小を比較せよ。ただし、自然対数の底eについて、2.7<e<2.8であることは用いてよい。
大問6
正の整数Nを3で割った時の余りは2である。
(1)正の整数a,bを3で割った時の余りをそれぞれ$r_a、r_b$とする。ab=Nが成り立つとき、$r_a、r_b$の組をすべて求めよ。
(2)Nの正の約数の総和を3で割った時の余りを求めよ。
(3)Nの正の約数の逆数の総和を$\displaystyle \frac{q}{p}$(ただし、pとqはともに正の整数で最大公約数は1である)と表したとき、qは3の倍数であることを示せ。
福田の数学〜上智大学2024TEAP利用型文系第3問(3)〜直線の回転

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
この動画を見る
$\boxed{3}(3)$座標平面において、直線$y=2x-3$を、原点を中心に反時計回りに45°回転して得られる直線は$y=\boxed{メ}x+\boxed{モ}\sqrt{\boxed{ヤ}}$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(2)〜角の二等分線の長さを求める
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
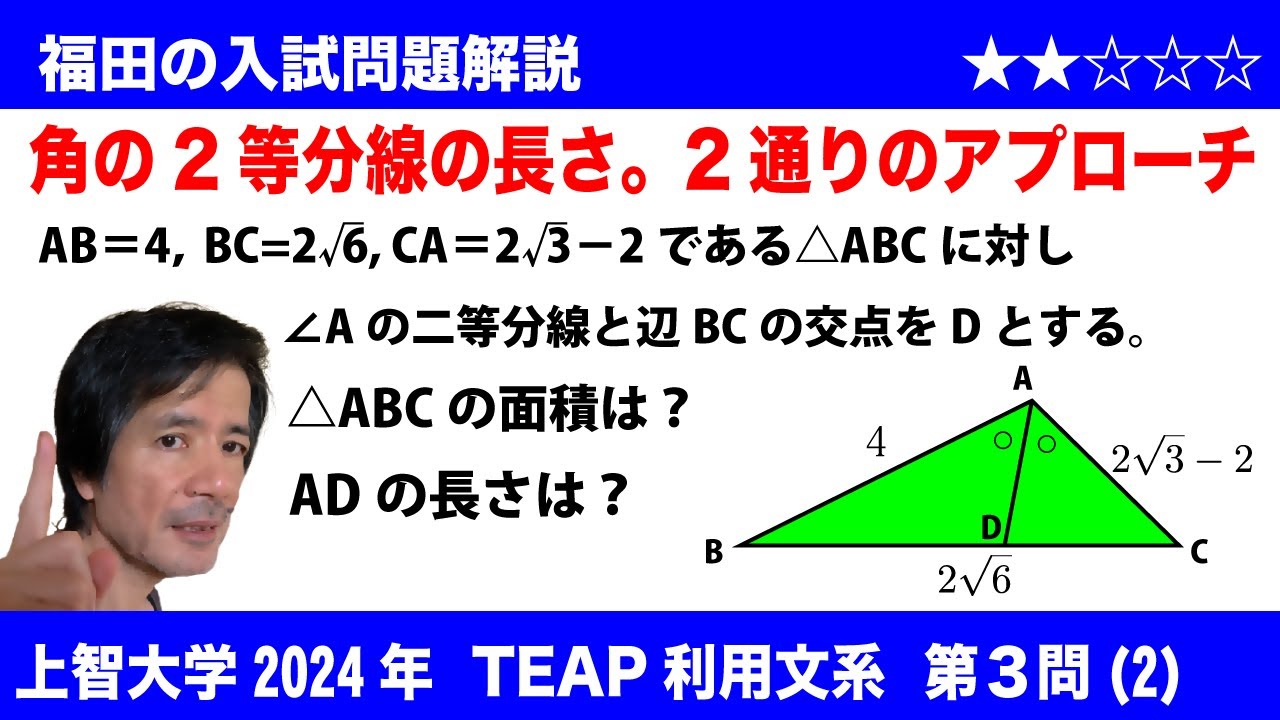
$\boxed{3}(2)AB=4,BC=2\sqrt{6},CA=2\sqrt{3}-2$の$\triangle ABC$がある。$\angle A$の二等分線と辺BCの交点をDとする。このとき、$\triangle ABC$の面積は$\boxed{フ}+\boxed{ヘ}\sqrt{\boxed{ホ}}$であり、$AD=\boxed{マ}+\boxed{ミ}\sqrt{\boxed{ム}}$である。
この動画を見る
$\boxed{3}(2)AB=4,BC=2\sqrt{6},CA=2\sqrt{3}-2$の$\triangle ABC$がある。$\angle A$の二等分線と辺BCの交点をDとする。このとき、$\triangle ABC$の面積は$\boxed{フ}+\boxed{ヘ}\sqrt{\boxed{ホ}}$であり、$AD=\boxed{マ}+\boxed{ミ}\sqrt{\boxed{ム}}$である。
福田の数学〜上智大学2024TEAP利用型文系第3問(1)〜対数指数不等式と領域に含まれる格子点の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
この動画を見る
$\boxed{3}(1)$整数の組$(x,y)$で条件\begin{eqnarray}
\left\{
\begin{array}{l}
\log_{ \frac{π}{4} } y \lt log_{\frac{1}{2}}(x-1) \\
2^{y-1} \lt 8^x
\end{array}
\right.
\end{eqnarray}
を満たすものは全部で$\boxed{ヒ}$個ある。
福田の数学〜上智大学2024TEAP利用型文系第2問〜2点の移動に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
表と裏が出る確率がそれぞれ $\frac{1}{2}$ である硬貨がある。座標平面において、原点 $(0,0)$ に置かれた点 $\mathrm{A}$ および座標 $(1,0)$ に置かれた点 $\mathrm{B}$ を、硬貨を $1$ 回投げるごとに以下の規則 $(R)$ に従って動かし、 $n$ 回硬貨を投げた直後における点 $\mathrm{A,B}$ の位置について考える。
規則 $(R)$:
・表が出たとき、 $\mathrm{A}$ は動かさず、 $\mathrm{B}$ は $\mathrm{A}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
・裏が出たとき、$\mathrm{B}$ は動かさず、 $\mathrm{A}$ は $\mathrm{B}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
$(1)$ $n=10$ のとき、$\overrightarrow{\mathrm{AB}}=(\fbox{タ},\fbox{チ})$
$(2)$ $n=3$ のとき、 $\mathrm{A}$ が位置することが可能な座標の総数は $\fbox{ツ}$ である。
$(3)$ $n=4$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{テ}}{\fbox{ト}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ナ}}{\fbox{ニ}}$ である。
$(4)$ $n=8$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{ヌ}}{\fbox{ネ}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ノ}}{\fbox{ハ}}$ である。
この動画を見る
表と裏が出る確率がそれぞれ $\frac{1}{2}$ である硬貨がある。座標平面において、原点 $(0,0)$ に置かれた点 $\mathrm{A}$ および座標 $(1,0)$ に置かれた点 $\mathrm{B}$ を、硬貨を $1$ 回投げるごとに以下の規則 $(R)$ に従って動かし、 $n$ 回硬貨を投げた直後における点 $\mathrm{A,B}$ の位置について考える。
規則 $(R)$:
・表が出たとき、 $\mathrm{A}$ は動かさず、 $\mathrm{B}$ は $\mathrm{A}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
・裏が出たとき、$\mathrm{B}$ は動かさず、 $\mathrm{A}$ は $\mathrm{B}$ を中心に反時計回りに $90^{\circ}$ 回転した位置に動かす。
$(1)$ $n=10$ のとき、$\overrightarrow{\mathrm{AB}}=(\fbox{タ},\fbox{チ})$
$(2)$ $n=3$ のとき、 $\mathrm{A}$ が位置することが可能な座標の総数は $\fbox{ツ}$ である。
$(3)$ $n=4$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{テ}}{\fbox{ト}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ナ}}{\fbox{ニ}}$ である。
$(4)$ $n=8$ のとき、 $\mathrm{A}$ が原点にある確率は $\displaystyle \frac{\fbox{ヌ}}{\fbox{ネ}}$ であり、 $\mathrm{A}$ が $x$ 軸上にある確率は $\displaystyle \frac{\fbox{ノ}}{\fbox{ハ}}$ である。
#同志社大学2021#定積分_62
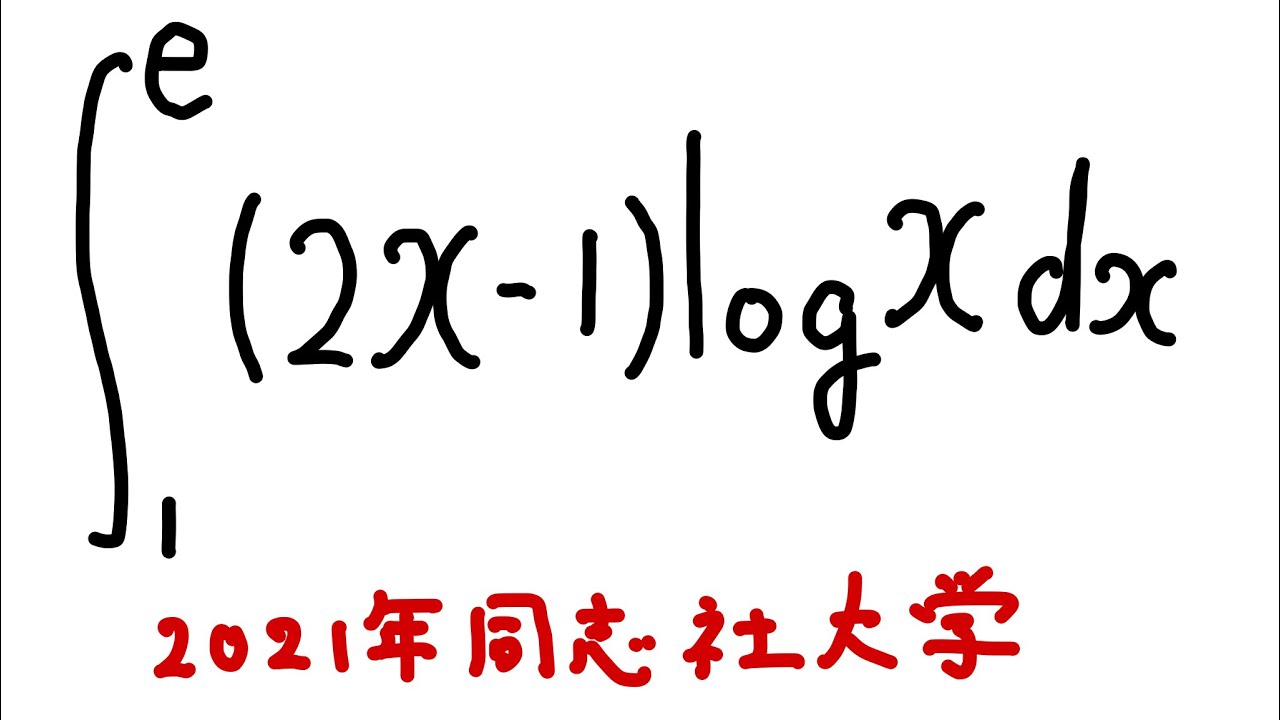
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#同志社大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (2x-1)\log x \ dx$を解け.
2021同志社大学過去問題
この動画を見る
$\displaystyle \int_{1}^{e} (2x-1)\log x \ dx$を解け.
2021同志社大学過去問題
#福岡大学医学部2018#極限_61
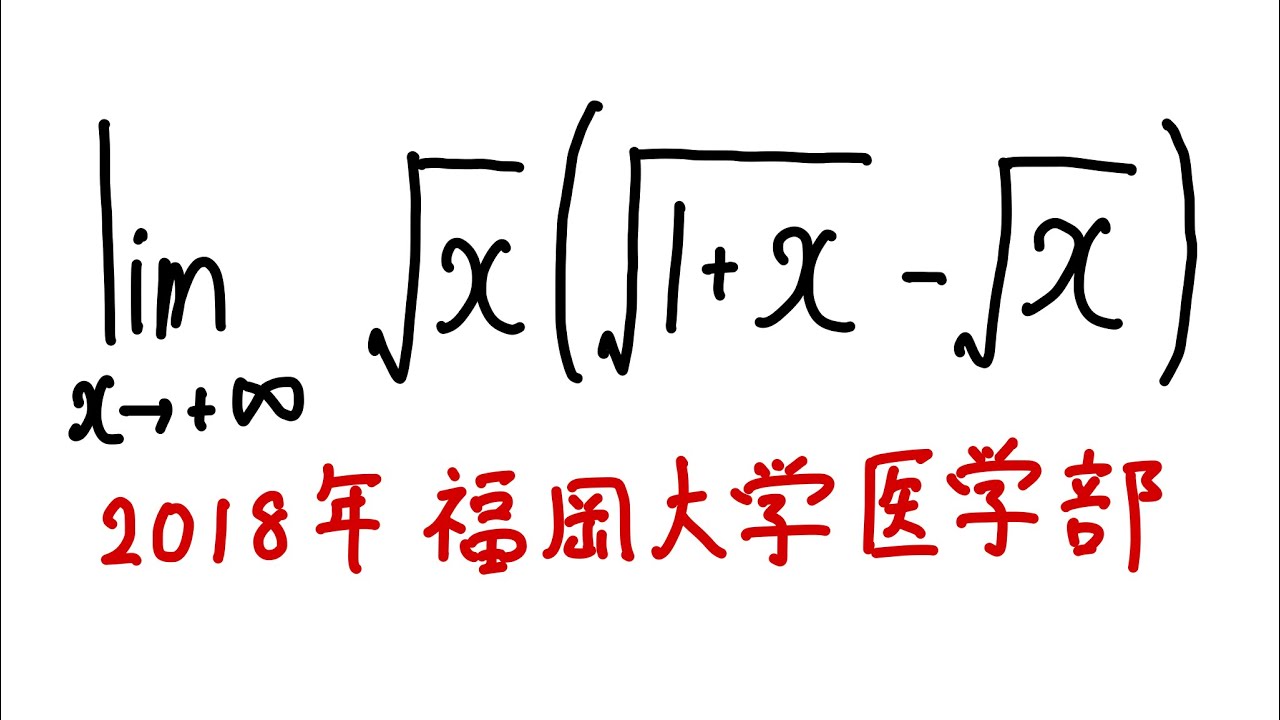
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} \sqrt x \left(\sqrt{1+x}-\sqrt x \right)$を解け.
2018福岡大学医学部過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} \sqrt x \left(\sqrt{1+x}-\sqrt x \right)$を解け.
2018福岡大学医学部過去問題
うおおおおお! 東京都市大学(武蔵工業大学)2004 大学入試問題#934

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#武蔵工業大学
指導講師:
ますただ
問題文全文(内容文):
連続関数$f(x)$で
$f(x)=e^x \displaystyle \int_{0}^{1} \{f(t)\}^2 dt$
を満たすものを求めよ.
2004東京都市大学過去問題
この動画を見る
連続関数$f(x)$で
$f(x)=e^x \displaystyle \int_{0}^{1} \{f(t)\}^2 dt$
を満たすものを求めよ.
2004東京都市大学過去問題
福田の数学〜上智大学2024TEAP利用型文系第1問〜正四面体に関する図形問題
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
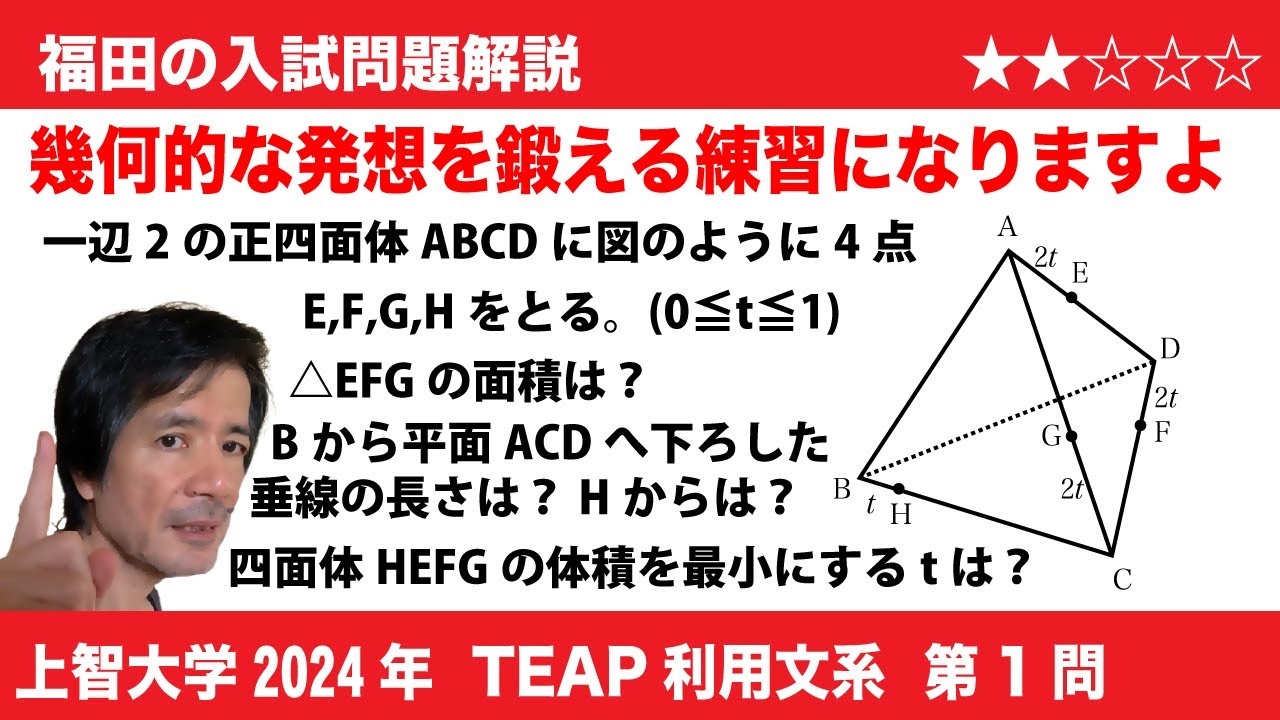
$1$ 辺の長さが $2$ の正四面体 $\mathrm{ABCD}$ において、辺 $\mathrm{AD}$ 上の点 $\mathrm{E}$、辺 $\mathrm{DC}$ 上の点 $\mathrm{F}$、辺 $\mathrm{CA}$ 上の点 $\mathrm{G}$、辺 $\mathrm{BC}$ 上の点 $\mathrm{H}$ を$\mathrm{AE}$$=\mathrm{DF}$$=\mathrm{CG}$$=2t,$ $\mathrm{BH}=t$ となるようにとる。ただし、 $0 \leqq t \leqq 1$ とする。
$(1)$ $\triangle \mathrm{EFG}$ の面積は $\sqrt{\fbox{ア}}(\fbox{イ}t^2$$+\fbox{ウ}t$$+\fbox{エ})$ である。
$(2)$ $\mathrm{B}$ から平面 $\mathrm{ACD}$ に垂線を下ろし、平面 $\mathrm{ACD}$ との交点を $\mathrm{P}$ とするとき、 $\mathrm{BP} = \frac{\fbox{オ}}{\fbox{カ}}\sqrt{\fbox{キ}}$ である。
$(3)$ $\mathrm{H}$ から平面 $\mathrm{EFG}$ に垂線を下ろし、平面 $\mathrm{EFG}$ との交点を $\mathrm{Q}$ とするとき、 $\mathrm{HQ} = \frac{\fbox{ク}}{\fbox{ケ}}\sqrt{\fbox{コ}}(t+\fbox{サ})$ である。
$(4)$ 四面体 $\mathrm{HEFG}$ の体積が最小になるのは
$t=\fbox{シ} + \frac{\fbox{ス}}{\fbox{セ}}\sqrt{\fbox{ソ}}$
この動画を見る
$1$ 辺の長さが $2$ の正四面体 $\mathrm{ABCD}$ において、辺 $\mathrm{AD}$ 上の点 $\mathrm{E}$、辺 $\mathrm{DC}$ 上の点 $\mathrm{F}$、辺 $\mathrm{CA}$ 上の点 $\mathrm{G}$、辺 $\mathrm{BC}$ 上の点 $\mathrm{H}$ を$\mathrm{AE}$$=\mathrm{DF}$$=\mathrm{CG}$$=2t,$ $\mathrm{BH}=t$ となるようにとる。ただし、 $0 \leqq t \leqq 1$ とする。
$(1)$ $\triangle \mathrm{EFG}$ の面積は $\sqrt{\fbox{ア}}(\fbox{イ}t^2$$+\fbox{ウ}t$$+\fbox{エ})$ である。
$(2)$ $\mathrm{B}$ から平面 $\mathrm{ACD}$ に垂線を下ろし、平面 $\mathrm{ACD}$ との交点を $\mathrm{P}$ とするとき、 $\mathrm{BP} = \frac{\fbox{オ}}{\fbox{カ}}\sqrt{\fbox{キ}}$ である。
$(3)$ $\mathrm{H}$ から平面 $\mathrm{EFG}$ に垂線を下ろし、平面 $\mathrm{EFG}$ との交点を $\mathrm{Q}$ とするとき、 $\mathrm{HQ} = \frac{\fbox{ク}}{\fbox{ケ}}\sqrt{\fbox{コ}}(t+\fbox{サ})$ である。
$(4)$ 四面体 $\mathrm{HEFG}$ の体積が最小になるのは
$t=\fbox{シ} + \frac{\fbox{ス}}{\fbox{セ}}\sqrt{\fbox{ソ}}$
#京都帝国大学1935#不定積分_60

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^2}}dx$を解け.
1935京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{x^2}{\sqrt{1-x^2}}dx$を解け.
1935京都帝国大学過去問題
#京都大学1937#極限_59

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
霊感強い系の受験者は、山勘でいける 関西医科大学2024 大学入試問題#933

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#関西医科大学
指導講師:
ますただ
問題文全文(内容文):
数列$\{an\}$を
$a_1=2,a_{n+1}=S_n-n(n-4)$
$(n=1,2,3・・・)$で定めるとき,$a_n$と$S_n$を
それぞれ$n$の式で表せ.
2024関西医科大学過去問題
この動画を見る
数列$\{an\}$を
$a_1=2,a_{n+1}=S_n-n(n-4)$
$(n=1,2,3・・・)$で定めるとき,$a_n$と$S_n$を
それぞれ$n$の式で表せ.
2024関西医科大学過去問題
#弘前大学2023#定積分_58

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{\sqrt{3+2x-x^2}}$を解け.
2023弘前大学過去問題
#弘前大学2023#定積分_57

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
この動画を見る
$\displaystyle \int_{1}^{2} \dfrac{dx}{3+2x-x^2}$を解け.
2023弘前大学過去問題
京大らしさ全開の不朽の名作 京都帝国大学1937 大学入試問題#932

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \dfrac{dx}{(x^2-1)^2}$を解け.
1937京都帝国大学過去問題
#弘前大学2024#定積分_56
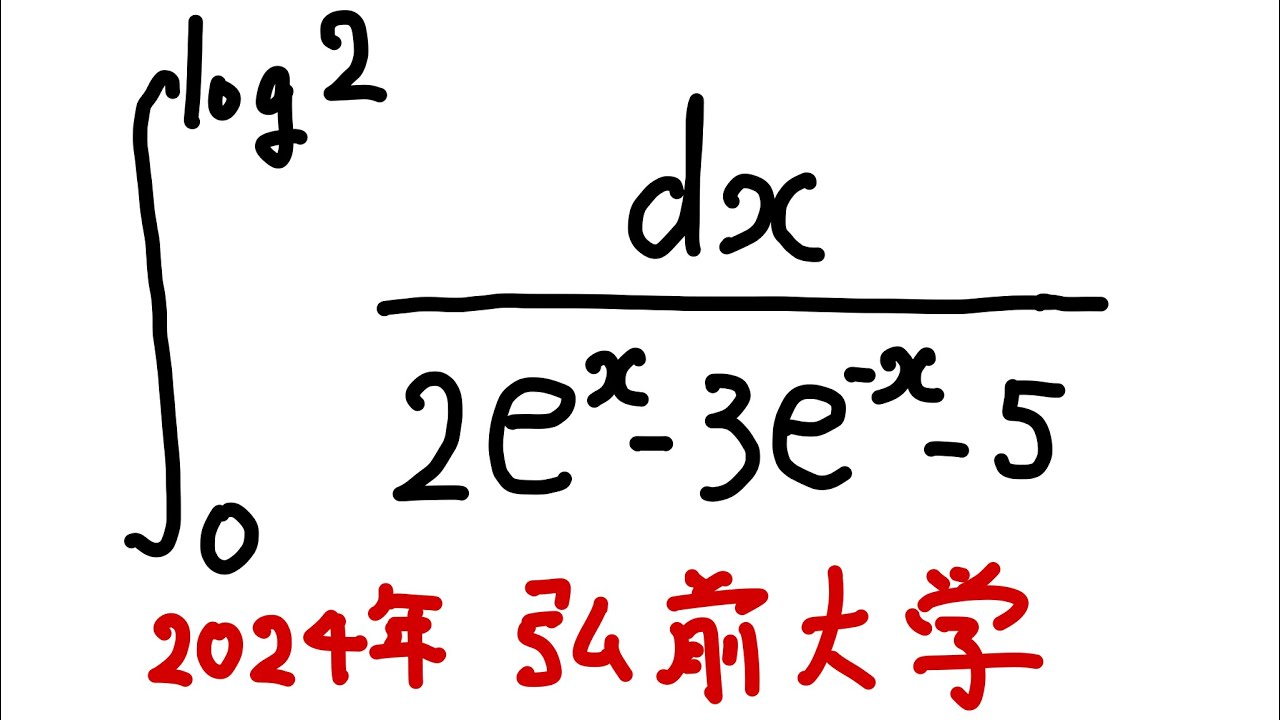
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#弘前大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
この動画を見る
$\displaystyle \int_{0}^{\log 2} \dfrac{dx}{2e^x-3e^{-x}-5}$を解け.
弘前大学過去問
