大学入試過去問(数学)
大学入試過去問(数学)
福田の数学〜京都大学2025理系第5問〜媒介変数表示で表された曲線
単元：
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#京都大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$\theta$は実数とする。
$xyz$空間の$2$点
$A\left(0,0,\dfrac{\sqrt2}{4}\right),P\left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right)$を
通る直線$AP$が$xy$平面と交わるとき、
その交点を$Q$とする。
$\theta$が$-\dfrac{\pi}{4}\lt \theta \lt \dfrac{\pi}{4}$の範囲を動くときの
点$Q$の軌跡を求め、その軌跡を$xy$平面上に図示せよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{5}$
$\theta$は実数とする。
$xyz$空間の$2$点
$A\left(0,0,\dfrac{\sqrt2}{4}\right),P\left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right)$を
通る直線$AP$が$xy$平面と交わるとき、
その交点を$Q$とする。
$\theta$が$-\dfrac{\pi}{4}\lt \theta \lt \dfrac{\pi}{4}$の範囲を動くときの
点$Q$の軌跡を求め、その軌跡を$xy$平面上に図示せよ。
$2025$年京都大学理系過去問題
2025年高校別東京大学合格者ランキング #shorts
単元：
#大学入試過去問(数学)#物理#学校別大学入試過去問解説(数学)#大学入試過去問(物理)#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#東京大学#数学(高校生)#理科(高校生)#東京大学#東京大学
指導講師：
Morite2 English Channel
問題文全文(内容文)：
2025年版！高校別東大合格者数ランキング速報がヤバい！
このランキングはまだ暫定版で、筑駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も**開成高校**で149人合格の圧倒的な強さを見せつけた。
そして注目すべきは公立高校の躍進だ！
* 第3位には**日比谷高校**がランクインし、公立ながら東大に81人も合格させている。
* 第7位には**横浜翠嵐高校**（神奈川県）が74人で食い込む。
* 第14位には**県立浦和**が41人で登場だ。
* さらに、**旭丘**（愛知）が28人、**千葉高校**（県立）が21人、**宇都宮**（栃木）が20人、**岡崎**（愛知）も20人と、全国の公立高校が猛追している！
私立ももちろん強い。2位が**聖光学院**（神奈川）で95人、4位**麻布**（79人）、5位**灘**（76人）、6位**渋谷教育学園幕張**（千葉、75人）と続く。神奈川勢は、聖光学院、横浜翠嵐、栄光学園（8位、55人）、浅野（9位、51人）と大健闘だ。
**渋渋（渋谷教育学園渋谷）が50人で10位**に入り、今年も伸びを見せつけているぞ。
このランキングを見れば、どの高校が東大合格戦線をリードしているのか一目瞭然だ。お前らの高校は何位だ！？
この動画を見る
2025年版！高校別東大合格者数ランキング速報がヤバい！
このランキングはまだ暫定版で、筑駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も駒の数字はまだ出ていないが、激アツな順位が明らかになったぞ。
栄えある第1位は、今年も**開成高校**で149人合格の圧倒的な強さを見せつけた。
そして注目すべきは公立高校の躍進だ！
* 第3位には**日比谷高校**がランクインし、公立ながら東大に81人も合格させている。
* 第7位には**横浜翠嵐高校**（神奈川県）が74人で食い込む。
* 第14位には**県立浦和**が41人で登場だ。
* さらに、**旭丘**（愛知）が28人、**千葉高校**（県立）が21人、**宇都宮**（栃木）が20人、**岡崎**（愛知）も20人と、全国の公立高校が猛追している！
私立ももちろん強い。2位が**聖光学院**（神奈川）で95人、4位**麻布**（79人）、5位**灘**（76人）、6位**渋谷教育学園幕張**（千葉、75人）と続く。神奈川勢は、聖光学院、横浜翠嵐、栄光学園（8位、55人）、浅野（9位、51人）と大健闘だ。
**渋渋（渋谷教育学園渋谷）が50人で10位**に入り、今年も伸びを見せつけているぞ。
このランキングを見れば、どの高校が東大合格戦線をリードしているのか一目瞭然だ。お前らの高校は何位だ！？
福田の数学〜京都大学2025理系第4問〜平面が定点を通過する条件
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{4}$
座標空間の$4$点$O,A,B,C$は同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、
直線$OB$上の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA },\overrightarrow{ OM }=t\overrightarrow{ OB },\overrightarrow{ ON }=u\overrightarrow{ OC }$が
成り立つようにとる。
(1)$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点$P$を通ることを示せ。
さらに、そのような点$P$はただ一つに定まることを示せ。
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第2問〜不定方程式で表された数の最小値
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{2}$
正の整数$x,y,z$を用いて
$N=9z^2=x^6+y^4$
と表される正の整数$N$の最小値を求めよ。
$2025$年京都大学理系過去問題
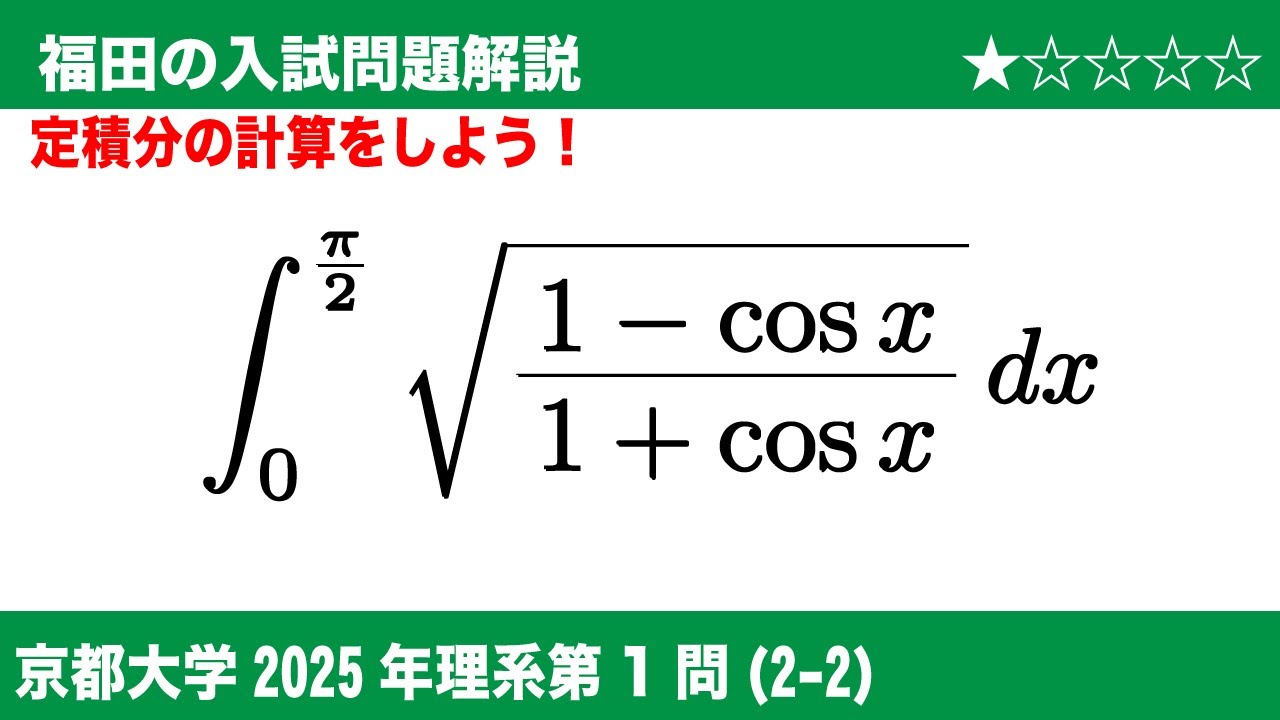
福田の数学〜京都大学2025理系第1問(2−2)〜定積分の計算
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-2)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{\dfrac{1-\cos x}{1+\cos x}}dx$
$2025$年京都大学理系過去問題
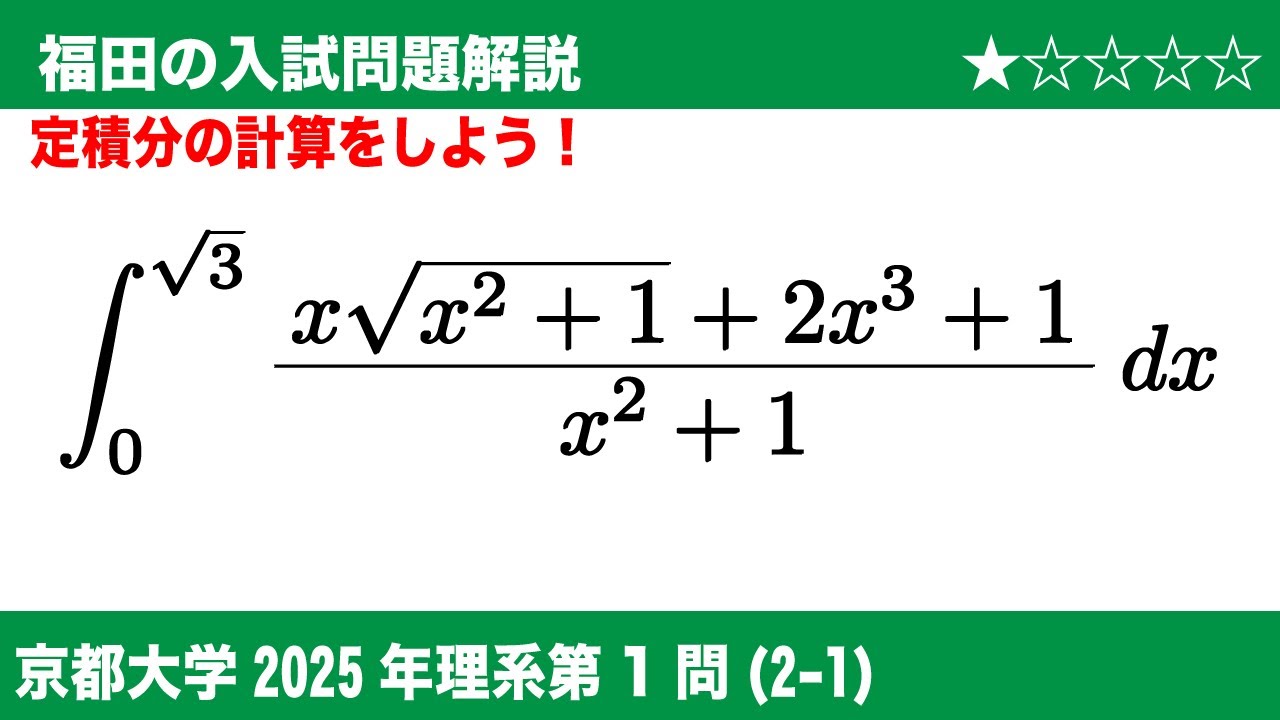
福田の数学〜京都大学2025理系第1問(2−1)〜定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第1問(1)〜複素数の絶対値の取り得る値の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
【高校数学】東京大学2025年度理系数学第2問 積分と極限の問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
■【東京大学 2025】
(1)$x＞1$のとき、不等式$logx≦x-1$を示せ。
(2)次の極限を求めよ。
$\displaystyle\lim_{n\to \infty}n\displaystyle \int_1^2log\displaystyle(\frac{1+x^{\frac{1}{n}}}{2})dx$
この動画を見る
■【東京大学 2025】
(1)$x＞1$のとき、不等式$logx≦x-1$を示せ。
(2)次の極限を求めよ。
$\displaystyle\lim_{n\to \infty}n\displaystyle \int_1^2log\displaystyle(\frac{1+x^{\frac{1}{n}}}{2})dx$
福田の数学〜東京大学2025文系第4問〜放物線で囲まれた面積の最大値
単元：
#連立方程式#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
この動画を見る
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
福田の数学〜東京大学2025文系第3問〜確率漸化式
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
白玉$2$個が横に並んでいる。
投げたとき表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインを用いて、
次の手順 (＊) をくり返し、
白玉または黒玉を横一列に並べていく。
手順(＊)
$\quad$コインを投げ、
$\quad$表が出たら白玉、裏が出たら黒玉を、
$\quad$それまでに並べられている一番右にある玉の
$\quad$右隣におく。
$\quad$そして、新しくおいた玉の色が
$\quad$その$1$つ左の玉の色と異なり、
$\quad$かつ$2$つ左の玉の色と一致するときには、
$\quad$新しくおいた玉の$1$つ左の玉を新しくおいた玉と
$\quad$同じ色の玉にとりかえる。
例えば、手順(＊)を$2$回行いコインが裏、表の順に
出た場合には、白玉が$4$つ並ぶ。
正の整数$n$に対して、手順(＊)を$n$回行った時点での
$(n + 2)$個の玉の並び方を考える。
(1)$n = 3$のとき、
右から$2$番目の玉が白玉である確率を求めよ。
(2)$n$を正の整数とする。
右から$2$番目の玉が白玉である確率を求めよ。
(3)$n$を正の整数とする。
右から$1$番目と$2$番目の玉がともに白玉である確率を求めよ。
$2025$年東京大学文系過去問題
この動画を見る
$\boxed{3}$
白玉$2$個が横に並んでいる。
投げたとき表と裏の出る確率が
それぞれ$\dfrac{1}{2}$のコインを用いて、
次の手順 (＊) をくり返し、
白玉または黒玉を横一列に並べていく。
手順(＊)
$\quad$コインを投げ、
$\quad$表が出たら白玉、裏が出たら黒玉を、
$\quad$それまでに並べられている一番右にある玉の
$\quad$右隣におく。
$\quad$そして、新しくおいた玉の色が
$\quad$その$1$つ左の玉の色と異なり、
$\quad$かつ$2$つ左の玉の色と一致するときには、
$\quad$新しくおいた玉の$1$つ左の玉を新しくおいた玉と
$\quad$同じ色の玉にとりかえる。
例えば、手順(＊)を$2$回行いコインが裏、表の順に
出た場合には、白玉が$4$つ並ぶ。
正の整数$n$に対して、手順(＊)を$n$回行った時点での
$(n + 2)$個の玉の並び方を考える。
(1)$n = 3$のとき、
右から$2$番目の玉が白玉である確率を求めよ。
(2)$n$を正の整数とする。
右から$2$番目の玉が白玉である確率を求めよ。
(3)$n$を正の整数とする。
右から$1$番目と$2$番目の玉がともに白玉である確率を求めよ。
$2025$年東京大学文系過去問題
【高校数学】京都大学の定積分の問題は半角の公式で攻略できた！
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
■【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int_0^{\frac{π}{2}}\sqrt{\frac{1-cosx}{1+cosx}}dx$
この動画を見る
■【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int_0^{\frac{π}{2}}\sqrt{\frac{1-cosx}{1+cosx}}dx$
福田の数学〜東京大学2025文系第2問〜三角形の3頂点を中心とする3つの円で3辺を含む条件と三角形を含む条件
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
平面上で$AB=AC=1$である
二等辺三角形$ABC$を考える。
正の実数$r$に対し、$A,B,C$それぞれを中心とする
半径$r$の円$3$つを合わせた領域を$D_r$とする。
ただし、この問いでは、
三角形と円は周とその内部からなるものとする。
辺$AB,AC,BC$がすべて$D_r$に
含まれるような最小の$r$を$s$、
三角形$ABC$が
$D_r$に含まれるような最小の$r$を$t$と表す。
(1)$\angle BAC=\dfrac{\pi}{3}$のとき、$s$と$t$を求めよ。
(2)$\angle BAC=\dfrac{2\pi}{3}$のとき、$s$と$t$を求めよ。
(3)$0\lt \theta \lt \pi$を満たす$\theta$に対して、
$\angle BAC=\theta$のとき、$s$と$t$を$\theta$を用いて表せ。
$2025$年東京大学文系過去問題
この動画を見る
$\boxed{2}$
平面上で$AB=AC=1$である
二等辺三角形$ABC$を考える。
正の実数$r$に対し、$A,B,C$それぞれを中心とする
半径$r$の円$3$つを合わせた領域を$D_r$とする。
ただし、この問いでは、
三角形と円は周とその内部からなるものとする。
辺$AB,AC,BC$がすべて$D_r$に
含まれるような最小の$r$を$s$、
三角形$ABC$が
$D_r$に含まれるような最小の$r$を$t$と表す。
(1)$\angle BAC=\dfrac{\pi}{3}$のとき、$s$と$t$を求めよ。
(2)$\angle BAC=\dfrac{2\pi}{3}$のとき、$s$と$t$を求めよ。
(3)$0\lt \theta \lt \pi$を満たす$\theta$に対して、
$\angle BAC=\theta$のとき、$s$と$t$を$\theta$を用いて表せ。
$2025$年東京大学文系過去問題
福田の数学〜東京大学2025文系第1問〜放物線とその法線の交点のx座標の最小値
単元：
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$a$を正の実数とする。
座標平面において、
放物線$C:y=x^2$上の点$P(a,a^2)$に
おける$C$の接線と直交し、$P$を通る直線を$\ell$とおく。
$\ell$と$C$の交点のうち、$P$と異なる点を$Q$と置く。
(1)$Q$の$x$座標を求めよ。
$Q$における$C$の接線と直交し、$Q$を通る直線を$m$とおく。
$m$と$C$の交点のうち、$Q$と異なる点を$R$とおく。
(2)$a$がすべての正の実数を動くとき、
$R$の$x$座標の最小値を求めよ。
$2025$年東京大学文系過去問題
この動画を見る
$\boxed{1}$
$a$を正の実数とする。
座標平面において、
放物線$C:y=x^2$上の点$P(a,a^2)$に
おける$C$の接線と直交し、$P$を通る直線を$\ell$とおく。
$\ell$と$C$の交点のうち、$P$と異なる点を$Q$と置く。
(1)$Q$の$x$座標を求めよ。
$Q$における$C$の接線と直交し、$Q$を通る直線を$m$とおく。
$m$と$C$の交点のうち、$Q$と異なる点を$R$とおく。
(2)$a$がすべての正の実数を動くとき、
$R$の$x$座標の最小値を求めよ。
$2025$年東京大学文系過去問題
福田の数学〜東京大学2025理系第6問〜複素数平面上の点の軌跡と実部の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{6}$
複素数平面上の点$\dfrac{1}{2}$を中心とする
半径$\dfrac{1}{2}$の円の周から原点を除いた曲線を
$C$とする。
(1)曲線$C$上の複素数$z$に対し、$\dfrac{1}{z}$の実部は
$1$であることを示せ。
(2)$\alpha,\beta$を曲線$C$上の相異なる複素数とするとき、
$\dfrac{1}{alpha^2}+\dfrac{1}{\beta^2}$がとりうる範囲を
複素数平面上に図示せよ。
(3)$\nu $を(2)で求めた範囲に属さない複素数とするとき、
$\dfrac{1}{\gamma}$の実部がとりうる値の
最大値と最小値を求めよ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{6}$
複素数平面上の点$\dfrac{1}{2}$を中心とする
半径$\dfrac{1}{2}$の円の周から原点を除いた曲線を
$C$とする。
(1)曲線$C$上の複素数$z$に対し、$\dfrac{1}{z}$の実部は
$1$であることを示せ。
(2)$\alpha,\beta$を曲線$C$上の相異なる複素数とするとき、
$\dfrac{1}{alpha^2}+\dfrac{1}{\beta^2}$がとりうる範囲を
複素数平面上に図示せよ。
(3)$\nu $を(2)で求めた範囲に属さない複素数とするとき、
$\dfrac{1}{\gamma}$の実部がとりうる値の
最大値と最小値を求めよ。
$2025$年東京大学理系過去問題
福田の数学〜東京大学2025理系第5問〜バブルソートが題材となった数が整列する条件を漸化式にする
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$n$を$2$以上の整数とする。
$1$から$n$までの数字が書かれた札が各$1$枚ずつ合計$n$枚あり、
横一列におかれている。
$1$以上$(n-1)$以下の整数$i$に対して、
次の操作$(T_i)$を考える。
$(T_i)$左から$i$番目の札の数字が、
左から$(i+1)$番目の札の数字よりも大きければ、
これら$2$枚の札の位置を入れ替える。
そうでなければ、札の位置を変えない。
最初の状態において札の数字は左から
$A_1,A_2,\cdots A_n$であったとする。
この状態から$(n-1)$回の操作$(T_1),(T_2),\cdots (T_{n-1})$を
順に行った後、続けて$(n-1)$回の操作
$(T_{n-1}),\cdots ,(T_2),(T_1)$を順に行ったところ、
札の数字は左から$1,2,\cdots ,n$と小さい順に並んだ。
以下の問いに答えよ。
(1)$A_1$と$A_2$の少なくとも一方は$2$以下であることを示せ。
(2)最初の状態としてありうる札の数字の並び方
$A_1,A_2,\cdots 、A_n$no総数を$c_n$とする。
$n$が$4$以上の整数であるとき、
$c_n$を$c_{n-1}$と$c_{n-2}$を用いて表せ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{5}$
$n$を$2$以上の整数とする。
$1$から$n$までの数字が書かれた札が各$1$枚ずつ合計$n$枚あり、
横一列におかれている。
$1$以上$(n-1)$以下の整数$i$に対して、
次の操作$(T_i)$を考える。
$(T_i)$左から$i$番目の札の数字が、
左から$(i+1)$番目の札の数字よりも大きければ、
これら$2$枚の札の位置を入れ替える。
そうでなければ、札の位置を変えない。
最初の状態において札の数字は左から
$A_1,A_2,\cdots A_n$であったとする。
この状態から$(n-1)$回の操作$(T_1),(T_2),\cdots (T_{n-1})$を
順に行った後、続けて$(n-1)$回の操作
$(T_{n-1}),\cdots ,(T_2),(T_1)$を順に行ったところ、
札の数字は左から$1,2,\cdots ,n$と小さい順に並んだ。
以下の問いに答えよ。
(1)$A_1$と$A_2$の少なくとも一方は$2$以下であることを示せ。
(2)最初の状態としてありうる札の数字の並び方
$A_1,A_2,\cdots 、A_n$no総数を$c_n$とする。
$n$が$4$以上の整数であるとき、
$c_n$を$c_{n-1}$と$c_{n-2}$を用いて表せ。
$2025$年東京大学理系過去問題
【高校数学】京都大学の定積分の問題はとにかく基本に忠実に！
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int _0^\sqrt{3}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
この動画を見る
【京都大学 2025】
次の定積分の値を求めよ。
$\displaystyle \int _0^\sqrt{3}\frac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
福田の数学〜東京大学2025理系第4問〜関数の値が平方数となる条件
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
福田の数学〜東京大学2025理系第3問〜平行四辺形を囲む長方形の面積の最大値
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed {3} $
平面四辺形$ABCD$において、
$\angle ABC = \dfrac {\pi} {6} , AB = a , BC = b , a \leqq b$とする。
次の条件を満たす長方形$EFGH$を考え、
その面積を$S$とする。
条件:点$A,B,C,D$はそれぞれ
$\quad$辺$EF,FG,GH,HE$上にある。
$\quad$ただし、辺はその両端の点も含むものとする。
(1)$\angle BCG=\theta$とするとき、
$S$を$a,b,\theta$を用いて表せ。
(2)$S$とりうる値の最大値を$a,b$を用いて表せ。
$2025$年東京大学理系過去問題
福田の数学〜東京大学2025理系第2問〜はさみうちの原理を利用する極限
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
福田の数学〜東京大学2025理系第1問〜媒介変数表示で表された曲線の面積と曲線の長さ
単元：
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東京大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
福田の数学〜旧・東京工業大学、東京科学大学2025理系第1問〜逆関数の定積分
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
この動画を見る
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
中央大学経済学部の数学で範囲外出題 #shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
Morite2 English Channel
問題文全文(内容文)：
まさかの事態発生！中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました！
今年の入まさかの事態発生！中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました！
今年の入試では、「整数問題は出題しない」としていたにも関わらず、受験生から「整数問題が出てるじゃないか」という声が複数上がっています。
今回問題視されているのは、「2025の正の約数のうち、素数でないものは何個あるか？」という問題。これは基本中の基本だという意見もあれば、「これは整数問題の範囲だからダメだろう」という意見も出ています。
中央大学経済学部の数学の範囲は、数学I・IIと、数学Aの「図形の性質」「場合の数と確率」と明記されています。この問題が、範囲外とされる整数問題とみなすべきなのか、それとも基礎的な問題として許容されるのか、専門家の間でも意見が分かれている状況です。
この問題、範囲内？それとも範囲外？数学の先生方の意見が待たれます！
この動画を見る
まさかの事態発生！中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました！
今年の入まさかの事態発生！中央大学経済学部の数学入試で、**出題範囲外**の疑惑が浮上しました！
今年の入試では、「整数問題は出題しない」としていたにも関わらず、受験生から「整数問題が出てるじゃないか」という声が複数上がっています。
今回問題視されているのは、「2025の正の約数のうち、素数でないものは何個あるか？」という問題。これは基本中の基本だという意見もあれば、「これは整数問題の範囲だからダメだろう」という意見も出ています。
中央大学経済学部の数学の範囲は、数学I・IIと、数学Aの「図形の性質」「場合の数と確率」と明記されています。この問題が、範囲外とされる整数問題とみなすべきなのか、それとも基礎的な問題として許容されるのか、専門家の間でも意見が分かれている状況です。
この問題、範囲内？それとも範囲外？数学の先生方の意見が待たれます！
【解答速報・全問解説】2025年2月1日 専修大学 全国入試 数学解答速報【理数大明神】
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大学入試解答速報#数学#専修大学#専修大学
指導講師：
理数個別チャンネル
問題文全文(内容文)：
こちらの動画は、2025年2月1日(土)に実施された、専修大学の数学の入試問題の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
解答だけ知りたい方はこちらから
https://note.com/kobetsu_teacher/n/n2062504ab208
この動画を見る
こちらの動画は、2025年2月1日(土)に実施された、専修大学の数学の入試問題の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
解答だけ知りたい方はこちらから
https://note.com/kobetsu_teacher/n/n2062504ab208
福田の数学〜過去の入試問題(期間限定)〜千葉大学理系2020第1問〜確率の基本性質
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
Aさんは1が書かれたカードを1枚、2が書かれたカードを2枚、4が書かれたカードを1枚、計4枚を無作為に横一列に並べて4桁の数Xを作る。Bさんは2が書かれたカードを2枚、3が書かれたカードを2枚、計4枚を無作為に横一列に並べて4桁の数Yを作る。
$$(1)Xが4の倍数となる確率を求めよ。
(2)X \lt Yとなる確率を求めよ。$$
この動画を見る
Aさんは1が書かれたカードを1枚、2が書かれたカードを2枚、4が書かれたカードを1枚、計4枚を無作為に横一列に並べて4桁の数Xを作る。Bさんは2が書かれたカードを2枚、3が書かれたカードを2枚、計4枚を無作為に横一列に並べて4桁の数Yを作る。
$$(1)Xが4の倍数となる確率を求めよ。
(2)X \lt Yとなる確率を求めよ。$$
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第4問〜正四面体の切り口の面積の最小値
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
oを原点とするxyz 空間内に、xy平面上の放物線y=x²をy軸のまわりに回転してできる曲面Sと、正四面体OABCがあり、条件「3頂点A, B, CはS上にある」をみたしている。このとき、次の問いに答えよ。
(1)正四面体 OABCの1辺の長さを求めよ。
(2)正四面体 OABCが条件をみたしながら動くとき、xy平面による正四面体OABCの切り口の面積の最小値を求めよ。
この動画を見る
oを原点とするxyz 空間内に、xy平面上の放物線y=x²をy軸のまわりに回転してできる曲面Sと、正四面体OABCがあり、条件「3頂点A, B, CはS上にある」をみたしている。このとき、次の問いに答えよ。
(1)正四面体 OABCの1辺の長さを求めよ。
(2)正四面体 OABCが条件をみたしながら動くとき、xy平面による正四面体OABCの切り口の面積の最小値を求めよ。
【解答速報・全問解説】2025年 大学入学共通テスト 数学ⅡBC解答速報
単元：
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師：
理数個別チャンネル
問題文全文(内容文)：
こちらの動画は、2025年1月19日(日)に実施された、2025年大学入学共通テストの数学ⅡBCの解答速報です。（LIVEで行った解答速報の抜粋版です）
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
指導講師：AKIYAMA、理数大明神、烈's study!、ゆう☆たろう
この動画を見る
こちらの動画は、2025年1月19日(日)に実施された、2025年大学入学共通テストの数学ⅡBCの解答速報です。（LIVEで行った解答速報の抜粋版です）
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
指導講師：AKIYAMA、理数大明神、烈's study!、ゆう☆たろう
【解答速報・全問解説】2025年 大学入学共通テスト 数学ⅠA解答速報
単元：
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師：
理数個別チャンネル
問題文全文(内容文)：
こちらの動画は、2025年1月19日(日)に実施された、2025年大学入学共通テストの数学ⅠAの解答速報です。（LIVEで行った解答速報の抜粋版です）
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
指導講師：AKIYAMA、理数大明神、烈's study!、ゆう☆たろう
この動画を見る
こちらの動画は、2025年1月19日(日)に実施された、2025年大学入学共通テストの数学ⅠAの解答速報です。（LIVEで行った解答速報の抜粋版です）
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
指導講師：AKIYAMA、理数大明神、烈's study!、ゆう☆たろう
共通テスト頑張った人に、今伝えたいこと
単元：
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
共通テストで絶望した人の溜まり場【カサニマロ ライブ】
単元：
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
共通テストを終えて_全部難しかったよ
単元：
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る