実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
福田のおもしろ数学576〜累乗根の大小比較
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
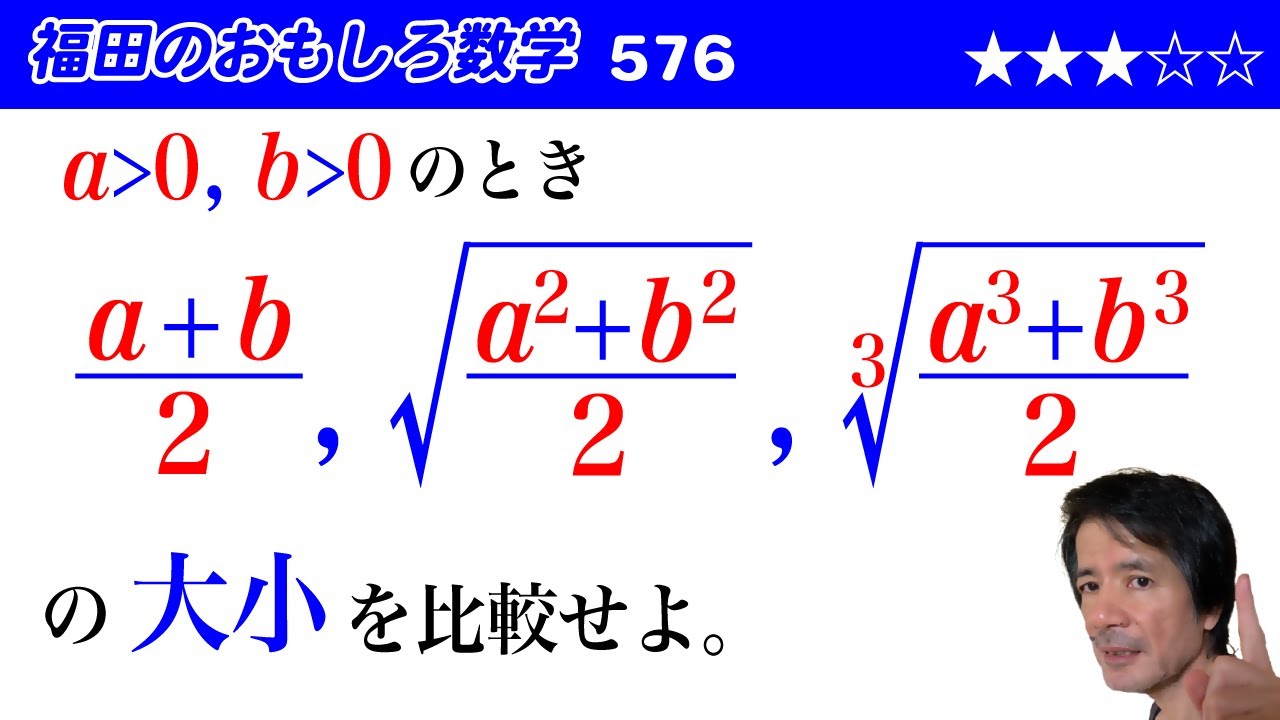
$a\gt 0,b \gt 0$のとき
$\dfrac{a+b}{2},\sqrt{\dfrac{a^2+b^2}{2}},\sqrt[3]{\dfrac{a^3+b^3}{2}}$
の大小を比較せよ。
この動画を見る
$a\gt 0,b \gt 0$のとき
$\dfrac{a+b}{2},\sqrt{\dfrac{a^2+b^2}{2}},\sqrt[3]{\dfrac{a^3+b^3}{2}}$
の大小を比較せよ。
福田のおもしろ数学575〜3乗根のついた2重根号の計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt[3]{20+14\sqrt2}+\sqrt[3]{20-14\sqrt2}$
を簡単にして下さい。
この動画を見る
$\sqrt[3]{20+14\sqrt2}+\sqrt[3]{20-14\sqrt2}$
を簡単にして下さい。
二乗せよ
ごめんなさい
【数A】【数と式】整数ｘが5個存在するようなaの値の範囲を求めよ。
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$7x-5 > 13-2x$
$x+a \geqq 3x+5$
整数$x$が5個存在するような$a$の値の範囲を求めよ。
この動画を見る
$7x-5 > 13-2x$
$x+a \geqq 3x+5$
整数$x$が5個存在するような$a$の値の範囲を求めよ。
【数A】【数と式】次のうち、小数点以下が√7 と同じになるのはどれ？
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次のうち、小数点以下が$\sqrt{7}$と同じになるのはどれ？
$\sqrt{11-4\sqrt{7}} $
$\sqrt{10-\sqrt{84}} $
$\sqrt{16-3\sqrt{28}} $
この動画を見る
次のうち、小数点以下が$\sqrt{7}$と同じになるのはどれ？
$\sqrt{11-4\sqrt{7}} $
$\sqrt{10-\sqrt{84}} $
$\sqrt{16-3\sqrt{28}} $
【数A】【数と式】つぎの等式のどこが間違えっているでしょう。√(4-2√3)=√(1+3-2√1・3)=√(√1-√3)²=√1-√3=1-√3
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の二重根号を外しなさい
$\sqrt{4-2\sqrt{3}} $
※解法に間違いがあるので
見つけましょう！
この動画を見る
次の二重根号を外しなさい
$\sqrt{4-2\sqrt{3}} $
※解法に間違いがあるので
見つけましょう！
【数A】【数と式】二重根号を外した形を求めよ(1) √(4+√7)(2) √(7-√33)(3) √(10+5√3)
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
二重根号を外した形を求めよ
(1) $\sqrt{4+\sqrt{7}} $
(2) $\sqrt{7-\sqrt{33}} $
(3) $\sqrt{10+5\sqrt{3}} $
この動画を見る
二重根号を外した形を求めよ
(1) $\sqrt{4+\sqrt{7}} $
(2) $\sqrt{7-\sqrt{33}} $
(3) $\sqrt{10+5\sqrt{3}} $
【数A】【数と式】二重根号を外した形を求めよ(1) √(5+√24） (2) √(11+4√6)(3) √(12-8√2）
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
二重根号を外した形を求めよ
(1) $\sqrt{5+\sqrt{24}} $
(2) $\sqrt{11+4\sqrt{6}} $
(3) $\sqrt{12-8\sqrt{2}} $
この動画を見る
二重根号を外した形を求めよ
(1) $\sqrt{5+\sqrt{24}} $
(2) $\sqrt{11+4\sqrt{6}} $
(3) $\sqrt{12-8\sqrt{2}} $
有理化の裏技ある？
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\frac{2}{\sqrt{2}}$, $\frac{10}{\sqrt{5}}$の分母を有理化せよ
この動画を見る
$\frac{2}{\sqrt{2}}$, $\frac{10}{\sqrt{5}}$の分母を有理化せよ
【数A】【数と式】二重根号を外した形を求めよ(1) √(4-2√3)(2) √(17-2√42)(3) √(9-2√20)
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#数と式#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
二重根号を外した形を求めよ
(1) $\sqrt{4-2\sqrt{3}} $
(2) $\sqrt{17-2\sqrt{42}} $
(3) $\sqrt{9-2\sqrt{20}} $
この動画を見る
二重根号を外した形を求めよ
(1) $\sqrt{4-2\sqrt{3}} $
(2) $\sqrt{17-2\sqrt{42}} $
(3) $\sqrt{9-2\sqrt{20}} $
福田の数学〜神戸大学2025理系第2問〜整数部分と小数部分
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
実数$a$に対して、$a$を超えない最大の整数を
$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}-n$とおく。
以下の問いに答えよ。
(1)$0\lt a_n \lt 1$が成り立つことを示せ。
(2)$b_n$を$\left(3n-\dfrac{1}{a_n}\right)$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めるものとする。
$m,n$を異なる$2$つの自然数とするとき、
$a_m+b_n \neq 1$であることを示せ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{2}$
実数$a$に対して、$a$を超えない最大の整数を
$k$とするとき、
$a-k$を$a$の小数部分という。
$n$を自然数とし、$a_n=\sqrt{n^2+1}-n$とおく。
以下の問いに答えよ。
(1)$0\lt a_n \lt 1$が成り立つことを示せ。
(2)$b_n$を$\left(3n-\dfrac{1}{a_n}\right)$の小数部分とする。
$b_n$を$n$を用いて表せ。
(3)$b_n$を(2)で定めるものとする。
$m,n$を異なる$2$つの自然数とするとき、
$a_m+b_n \neq 1$であることを示せ。
$2025$年神戸大学理系過去問題
【この一本でルートのルール全部確認!!】平方根の基礎全まとめ(平方根とは・有理化・乗法除法・加法減法 )〔現役講師解説、中学数学・高校数学〕
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
次の数の平方根は？
①$4$
②$0.01$
③$3$
④$0.2$
平方根を使わずに表しなさい。
①$\sqrt4$
②$-\sqrt{25}$
③$(\sqrt3)^2$
④$(-\sqrt5)^2$
次の計算をせよ。
①$\sqrt3\times \sqrt2$
②$\sqrt5 \times \sqrt7 $
③$\sqrt6 \div \sqrt3$
④$\sqrt{45} \div \sqrt5$
$a\sqrt b$の形にせよ。
①$\sqrt{20}$
②$\sqrt{48}$
有理化しなさい。
①$\dfrac{3}{7}$
②$\dfrac{1}{12}$
次の計算をしなさい。
①$2\sqrt2 +3\sqrt2$
②$4\sqrt3-2\sqrt3$
③$2\sqrt3+2\sqrt2+4\sqrt3-5\sqrt2$
④$\sqrt{28}-3\sqrt7$
⑤$\sqrt2+\sqrt8-6\sqrt2$
この動画を見る
次の数の平方根は？
①$4$
②$0.01$
③$3$
④$0.2$
平方根を使わずに表しなさい。
①$\sqrt4$
②$-\sqrt{25}$
③$(\sqrt3)^2$
④$(-\sqrt5)^2$
次の計算をせよ。
①$\sqrt3\times \sqrt2$
②$\sqrt5 \times \sqrt7 $
③$\sqrt6 \div \sqrt3$
④$\sqrt{45} \div \sqrt5$
$a\sqrt b$の形にせよ。
①$\sqrt{20}$
②$\sqrt{48}$
有理化しなさい。
①$\dfrac{3}{7}$
②$\dfrac{1}{12}$
次の計算をしなさい。
①$2\sqrt2 +3\sqrt2$
②$4\sqrt3-2\sqrt3$
③$2\sqrt3+2\sqrt2+4\sqrt3-5\sqrt2$
④$\sqrt{28}-3\sqrt7$
⑤$\sqrt2+\sqrt8-6\sqrt2$
福田のおもしろ数学501〜√5+√6+…+√13の整数部分が26であることの証明
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt5+\sqrt6+\cdots +\sqrt{13}$
の整数部分が$26$であることを示せ。
この動画を見る
$\sqrt5+\sqrt6+\cdots +\sqrt{13}$
の整数部分が$26$であることを示せ。
福田のおもしろ数学500〜循環形式の連立方程式を解こう
単元：
#連立方程式#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y^2+6)=y(x^2+1) \\
(y-1)(x^2+6)=x(y^2+1)
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y$をすべて求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y^2+6)=y(x^2+1) \\
(y-1)(x^2+6)=x(y^2+1)
\end{array}
\right.
\end{eqnarray}$
を満たす実数$x,y$をすべて求めて下さい。
福田のおもしろ数学494〜3乗根の付いた数の大小比較
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
この動画を見る
大小を比較せよ。
$\sqrt[3]{4(2197+2025)}$
VS
$13+\sqrt[3]{2025}$
福田のおもしろ数学490〜3乗根混じりの2重根号を解消
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
この動画を見る
$\sqrt[3]{1342\sqrt{167}+2005}$
の$2$重根号を解消せよ。
福田のおもしろ数学486〜1分チャレンジ！無理数の計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
この動画を見る
$x=\dfrac{\sqrt6+\sqrt2+\sqrt3+2}{\sqrt6-\sqrt2+\sqrt3-2},$
$y=\dfrac{\sqrt6+\sqrt2-\sqrt3-2}{\sqrt6-\sqrt2-\sqrt3+2}$
のとき$x^5+y^5$の値を求めて下さい。
福田の数学〜慶應義塾大学看護医療学部2025第1問(1)〜分母の有理化
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
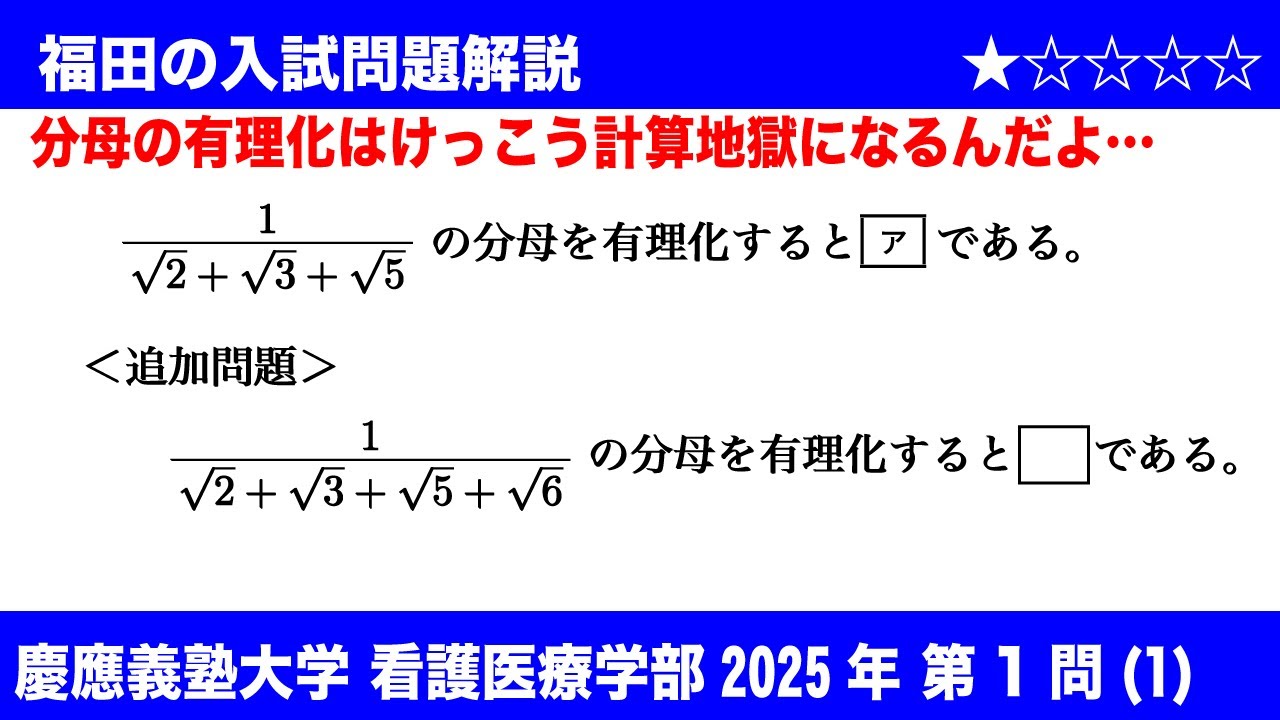
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{1}$
(1)$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5}$の分母を有理化すると
$\boxed{ア}$である。
〈追加問題〉
$\dfrac{1}{\sqrt2+\sqrt3+\sqrt5+\sqrt6}$の分母を有理化すると
$\Box$である。
$2025$年慶應義塾大学看護医療学部過去問題
福田のおもしろ数学474〜3変数の関係からa+b+cの値を求める
単元：
#連立方程式#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
この動画を見る
実数$a,b,c$が次の条件を満たしている。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2+b^2+c^2=1 \\
a^3+b^3+c^3=1
\end{array}
\right.
\end{eqnarray}$
$a+b+c$の値を求めよ。
福田のおもしろ数学428〜√n+1-√n-1が有理数になるような整数nが存在するかどうかを考える
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{n+1}-\sqrt{n-1}$が有理数となる
整数$n$は存在するか？
この動画を見る
$\sqrt{n+1}-\sqrt{n-1}$が有理数となる
整数$n$は存在するか？
福田の数学〜東京大学2025理系第4問〜関数の値が平方数となる条件
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{4}$
この問いでは、
$0$以上の整数の$2$乗になる数を平方数と呼ぶ。
$a$を正の整数とし、
$f_a (x) = x^2+x-a$とおく。
(1)$n$を正の整数とする。
$f_a(n)$は平方数ならば、$n\leqq a$であることを示せ。
(2)$f_a (n)$が平方数となる正の整数$n$の個数を
$N_a$とおく。
次の条件$(i),(ii)$が同値であることを示せ。
$(i)\quad N_a=1$である。
$(ii)\quad 4a+1$は素数である。
$2025$年東京大学理系過去問題
福田のおもしろ数学410〜条件を満たすKの最大値
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
この動画を見る
次の貢献を満たす実数$k$の最大値は？
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
福田のおもしろ数学396〜和が0のn個の実数に対して隣接2項の積の総和が0以下となるnは
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n\geqq 3$のとき、
$a_1+a_2+\cdots+a_n=0$を
満たすすべての実数$a_1,a_2\cdots a_n$について
$a_1a_2+a_2a_3+\cdots+a_{n-1}a_n+a_na_1 \leqq 0$
が成り立つような整数$n$をすべて求めよ。
この動画を見る
$n\geqq 3$のとき、
$a_1+a_2+\cdots+a_n=0$を
満たすすべての実数$a_1,a_2\cdots a_n$について
$a_1a_2+a_2a_3+\cdots+a_{n-1}a_n+a_na_1 \leqq 0$
が成り立つような整数$n$をすべて求めよ。
平方根 最大の整数 香川誠陵
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
${3\sqrt{2} }$以下の実数のうち、最大の整数を求めよ
この動画を見る
${3\sqrt{2} }$以下の実数のうち、最大の整数を求めよ
福田のおもしろ数学372〜絶対値の付いた式に関する証明
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
整数$a,b,c,d$は$|ac+bd|=|ad+bc|=1$を満たしている。このとき、次を示せ。
$|a|=|b|=1$ or $|c|=|d|=1$
この動画を見る
整数$a,b,c,d$は$|ac+bd|=|ad+bc|=1$を満たしている。このとき、次を示せ。
$|a|=|b|=1$ or $|c|=|d|=1$
【重要なルートを進め…！】平方根：渋谷教育学園幕張高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)#渋谷教育学園幕張高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$次の計算をしなさい。$
$\sqrt{(\sqrt{3}-1)^2}+\sqrt{(\sqrt{3}-2)^2}+\dfrac{1-\sqrt{3}}{2-\sqrt{3}}$
この動画を見る
$次の計算をしなさい。$
$\sqrt{(\sqrt{3}-1)^2}+\sqrt{(\sqrt{3}-2)^2}+\dfrac{1-\sqrt{3}}{2-\sqrt{3}}$
福田のおもしろ数学345〜複雑な2重根号の式が整数となる条件
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{ \mathstrut \frac{25}{2} +\sqrt{ \mathstrut \frac{625}{4} -n}}$+$\sqrt{ \mathstrut \frac{25}{2} -\sqrt{ \mathstrut \frac{625}{4} -n}}$が整数となるような整数$n$をすべて求めよ。
この動画を見る
$\sqrt{ \mathstrut \frac{25}{2} +\sqrt{ \mathstrut \frac{625}{4} -n}}$+$\sqrt{ \mathstrut \frac{25}{2} -\sqrt{ \mathstrut \frac{625}{4} -n}}$が整数となるような整数$n$をすべて求めよ。
【素早く解くには…！】文字式：青雲高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)#青雲高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x=\dfrac{3\sqrt{2}+2\sqrt{3}}{3},y=\dfrac{3\sqrt{2}-2\sqrt{3}}{2}のとき、$
$9x^2-4y^2の値を求めよ。$
この動画を見る
$x=\dfrac{3\sqrt{2}+2\sqrt{3}}{3},y=\dfrac{3\sqrt{2}-2\sqrt{3}}{2}のとき、$
$9x^2-4y^2の値を求めよ。$
【初見では固まる…！】平方根：慶応義塾高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)#慶應義塾高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$次の式を計算せよ。$
$\dfrac{1}{(1+\sqrt{2}+\sqrt{3})^2}+\dfrac{1}{(1+\sqrt{2}-\sqrt{3})^2}$
この動画を見る
$次の式を計算せよ。$
$\dfrac{1}{(1+\sqrt{2}+\sqrt{3})^2}+\dfrac{1}{(1+\sqrt{2}-\sqrt{3})^2}$