 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
 実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
中学生でも理解可能。ルートの中の二乗 奈良大
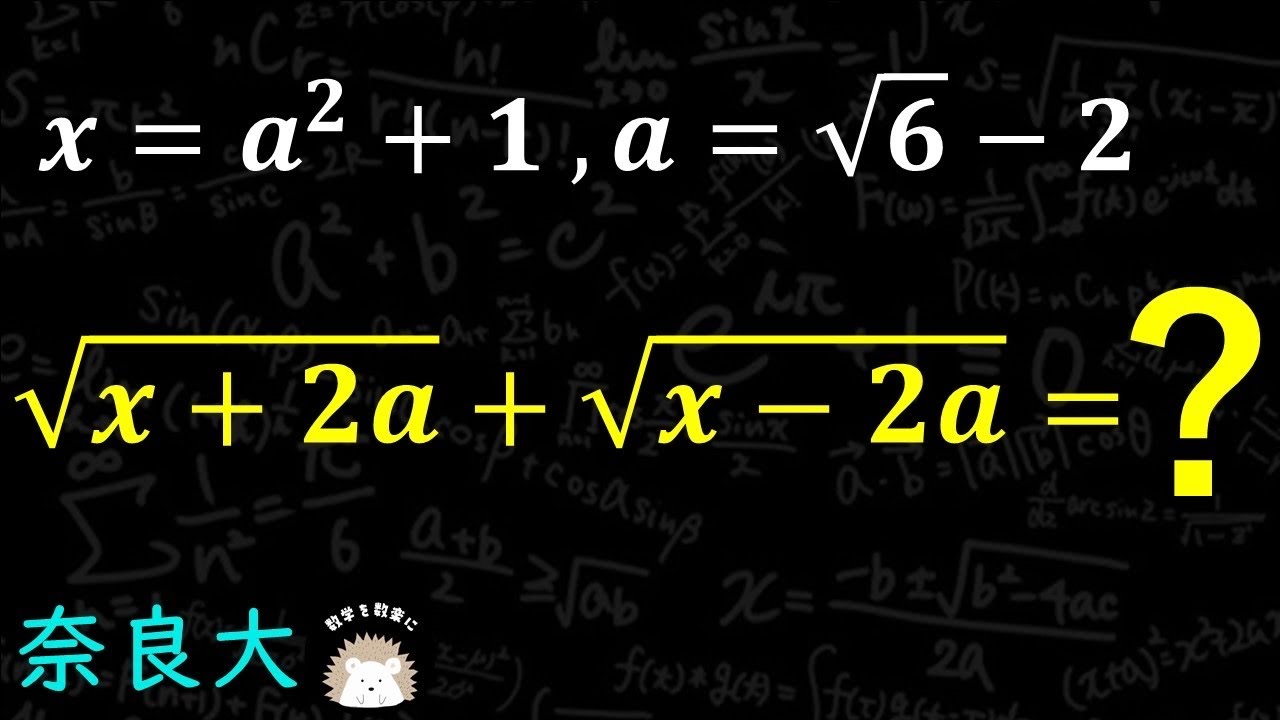
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=a^2+1$ , $a=\sqrt 6 -2$
$\sqrt {x+2a} + \sqrt {x-2a} =?$
奈良大学
この動画を見る
$x=a^2+1$ , $a=\sqrt 6 -2$
$\sqrt {x+2a} + \sqrt {x-2a} =?$
奈良大学
自宅で勉強してて分からない問題に当たった時の解決法 #shorts #勉強法 #勉強
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
自宅で勉強してて分からない問題に当たった時の解決法に関して解説していきます.
この動画を見る
自宅で勉強してて分からない問題に当たった時の解決法に関して解説していきます.
【7分でマスター!!】循環小数と分数の問題を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
循環小数と分数について解説します。
循環小数$1.\dot{5}$、$0.\dot{6}\dot{3}$をそれぞれ分数で表せ。
$\frac{30}{7}$を小数で表したとき、小数第100位の数字を求めよ。
この動画を見る
数学1A
循環小数と分数について解説します。
循環小数$1.\dot{5}$、$0.\dot{6}\dot{3}$をそれぞれ分数で表せ。
$\frac{30}{7}$を小数で表したとき、小数第100位の数字を求めよ。
平方根 津田塾大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数nで$\sqrt{n^2-n+20}$の整数部分がnとなるのは全部でいくつ?(n:自然数)
津田塾大学
この動画を見る
自然数nで$\sqrt{n^2-n+20}$の整数部分がnとなるのは全部でいくつ?(n:自然数)
津田塾大学
分母の有理化 愛知大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
分母を有理化せよ
$\frac{1}{\sqrt2+\sqrt3+2+\sqrt6}$
愛知大学
この動画を見る
分母を有理化せよ
$\frac{1}{\sqrt2+\sqrt3+2+\sqrt6}$
愛知大学
ルートを外せ15

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{\frac{n^2+297}{n^2+1}}$が整数となる整数nをすべて求めよ
2022中央大学附属高等学校
この動画を見る
$\sqrt{\frac{n^2+297}{n^2+1}}$が整数となる整数nをすべて求めよ
2022中央大学附属高等学校
【比例式】いきなり文字で置くな!【数学 入試問題】【福島大学】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
正の実数$x,y,z$が$\dfrac{yz}{x}=\dfrac{zx}{4y}=\dfrac{xy}{9z}$を満たすとき、$\dfrac{x+y+Z}{\sqrt{x^2+y^2+z^2}}$の値は?
福島大過去問
この動画を見る
正の実数$x,y,z$が$\dfrac{yz}{x}=\dfrac{zx}{4y}=\dfrac{xy}{9z}$を満たすとき、$\dfrac{x+y+Z}{\sqrt{x^2+y^2+z^2}}$の値は?
福島大過去問
cos1°は有理数か【数学 入試問題】【チェビシェフ多項式】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
この動画を見る
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
【有名問題】京都大学の伝説の問題です【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ tan1°$は有理数か?
数学入試問題過去問
この動画を見る
$ tan1°$は有理数か?
数学入試問題過去問
中国Jr 数学Olympicその2

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \left[\dfrac{10^{93}}{10^{31}+3}\right]$の下2桁の数を求めよ.
中国jr数学オリンピック過去問
この動画を見る
$ \left[\dfrac{10^{93}}{10^{31}+3}\right]$の下2桁の数を求めよ.
中国jr数学オリンピック過去問
格子点を通るということは?【山口大学】【数学 入試問題】
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
この動画を見る
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
平方根と式の値

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y=4$ , $xy=2$ , $x-y>0$
$\frac{\sqrt x - \sqrt y }{\sqrt x + \sqrt y } =?$
県立広島女子大学
この動画を見る
$x+y=4$ , $xy=2$ , $x-y>0$
$\frac{\sqrt x - \sqrt y }{\sqrt x + \sqrt y } =?$
県立広島女子大学
√と二乗
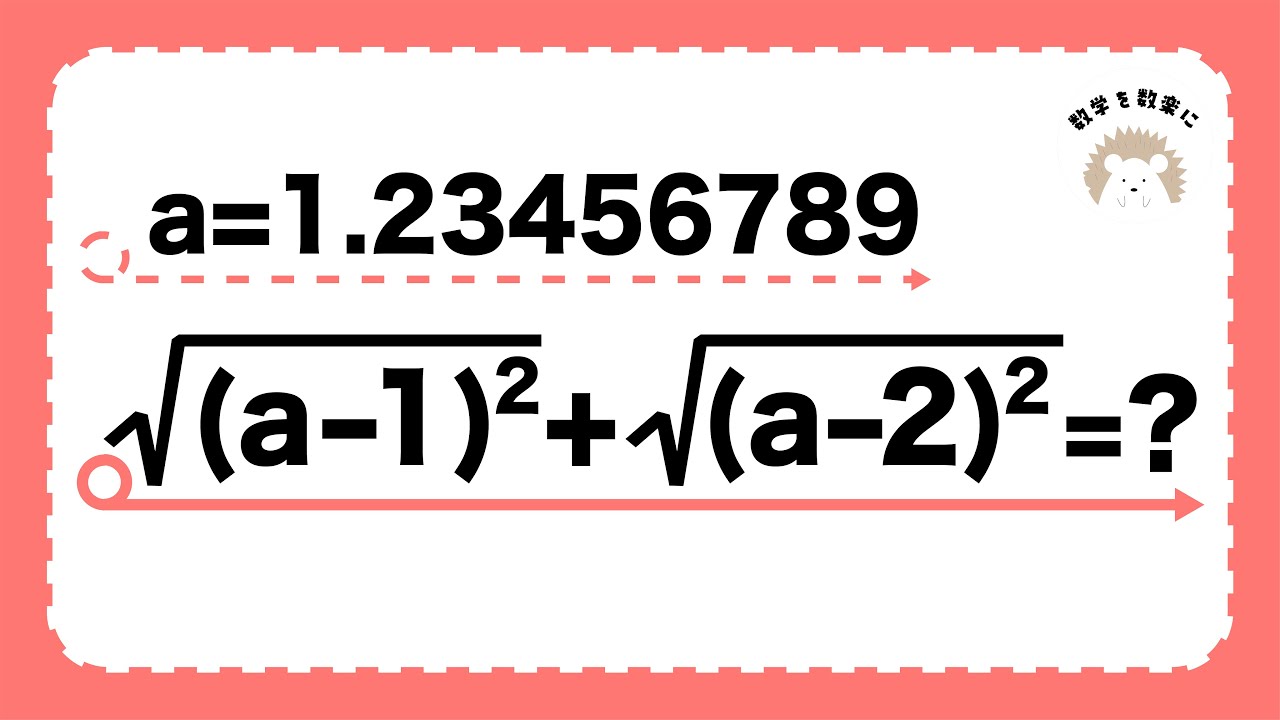
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a=1.23456789
$\sqrt{(a-1)^2} +\sqrt{(a-2)^2}=?$
この動画を見る
a=1.23456789
$\sqrt{(a-1)^2} +\sqrt{(a-2)^2}=?$
どっちがでかい?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$3^{\sqrt5}$ VS $5^{\sqrt3}$
この動画を見る
どちらが大きいか?
$3^{\sqrt5}$ VS $5^{\sqrt3}$
変な問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{2\sqrt{4\sqrt{8\sqrt{16\sqrt{32\sqrt{\sqrt64・・・・・・・・}}}}}}$
これを解け.
この動画を見る
$ \sqrt{2\sqrt{4\sqrt{8\sqrt{16\sqrt{32\sqrt{\sqrt64・・・・・・・・}}}}}}$
これを解け.
すっきり、あっさり

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ z=1+\sqrt[5]{2}+\sqrt[5]{4}+\sqrt[5]{8}+\sqrt[5]{16}$である.
$ \left(1+\dfrac{1}{z}\right)^{50}$の値を求めよ.
この動画を見る
$ z=1+\sqrt[5]{2}+\sqrt[5]{4}+\sqrt[5]{8}+\sqrt[5]{16}$である.
$ \left(1+\dfrac{1}{z}\right)^{50}$の値を求めよ.
3乗根を外すだけ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
3乗根を外せ.
$\sqrt[3]{\dfrac{10-7\sqrt2}{10+7\sqrt2}}$
この動画を見る
3乗根を外せ.
$\sqrt[3]{\dfrac{10-7\sqrt2}{10+7\sqrt2}}$
バサバサ消えるやつ 栄東高校
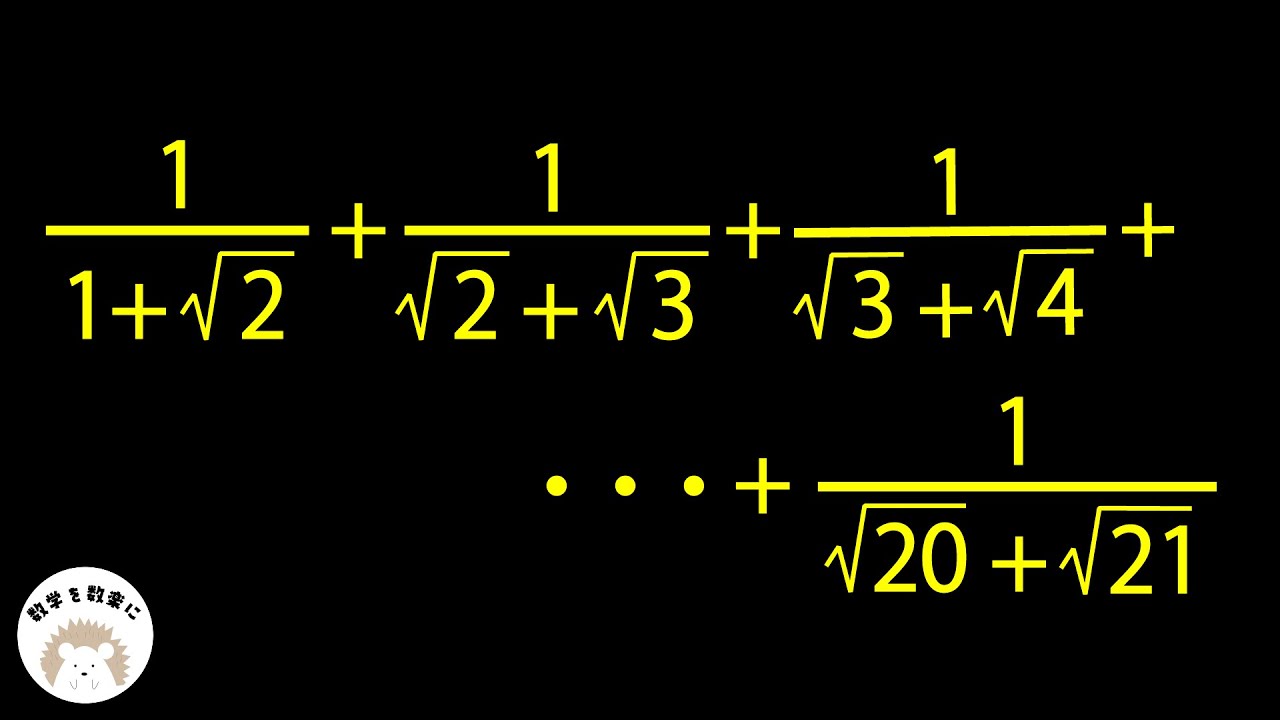
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
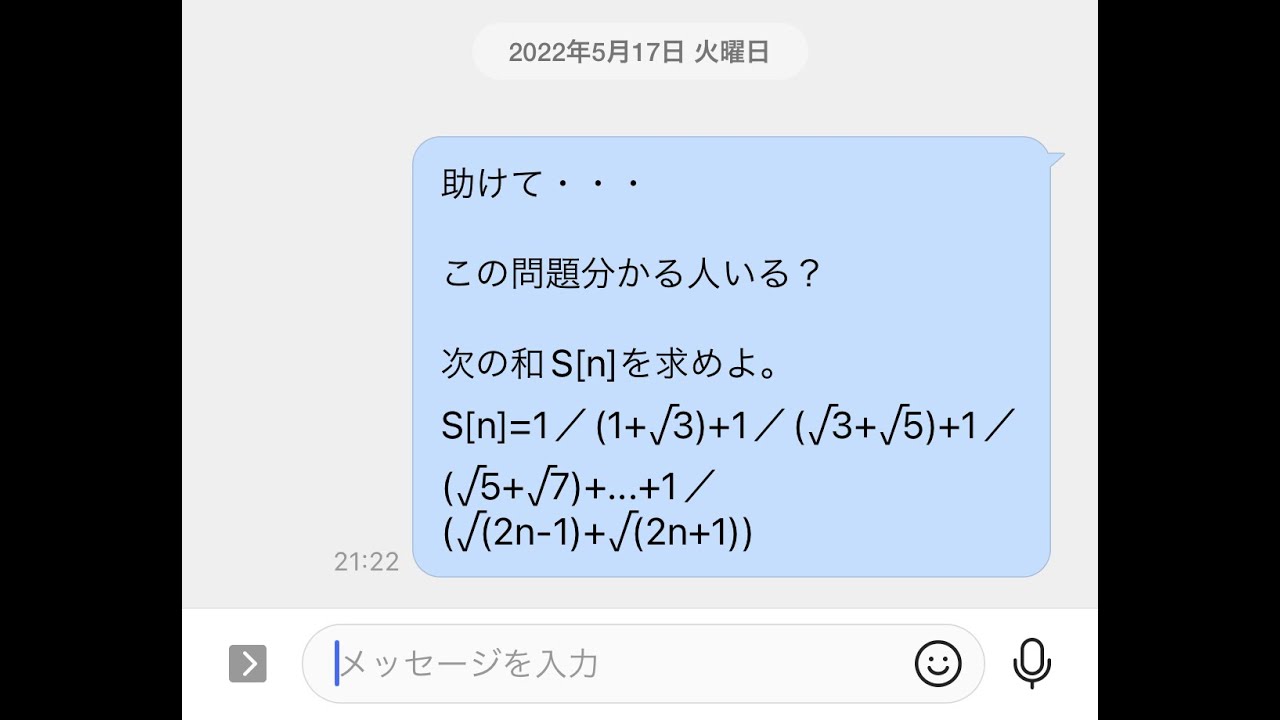
$\frac{1}{1+\sqrt 2} + \frac{1}{\sqrt 2+\sqrt 3} + \frac{1}{\sqrt 3+\sqrt 4} +
\cdots +\frac{1}{\sqrt {20}+\sqrt {21}}=?$
栄東高等学校
この動画を見る
$\frac{1}{1+\sqrt 2} + \frac{1}{\sqrt 2+\sqrt 3} + \frac{1}{\sqrt 3+\sqrt 4} +
\cdots +\frac{1}{\sqrt {20}+\sqrt {21}}=?$
栄東高等学校
平方根の計算 愛知県令和4年度 2022 入試問題100題解説87問目!
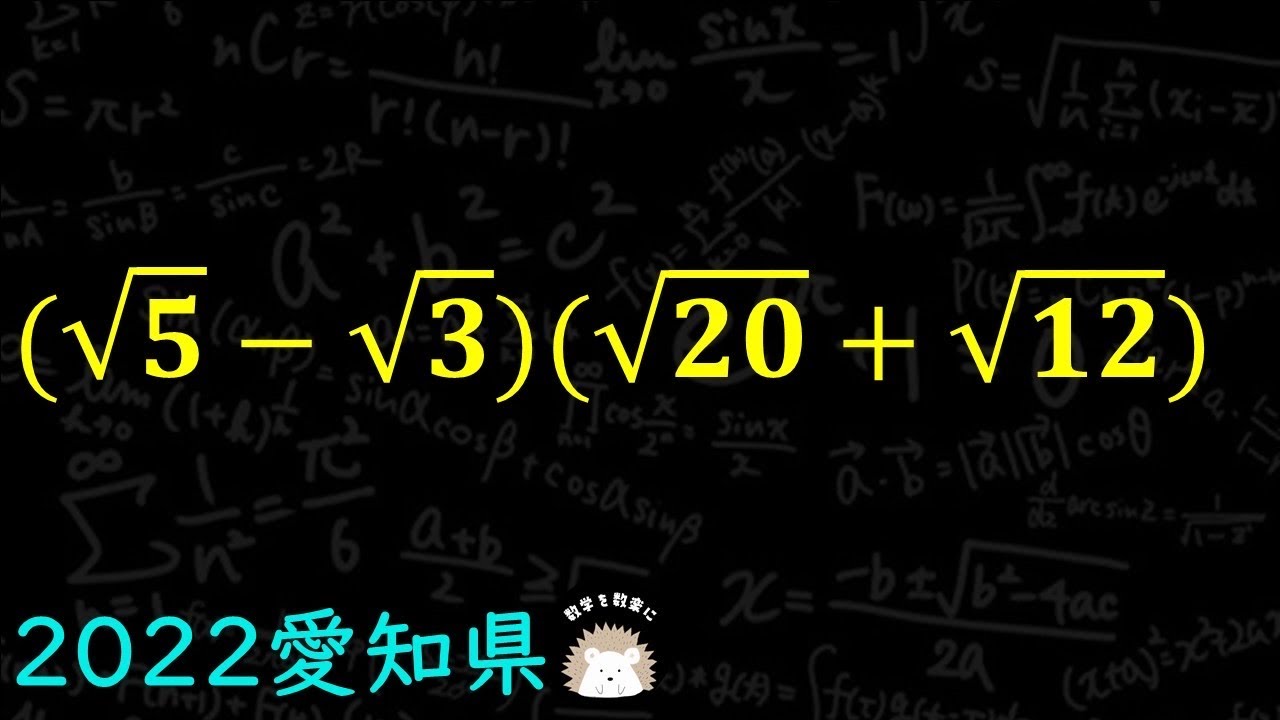
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 5 - \sqrt 3 )(\sqrt {20} + \sqrt {12} )$
2022愛知県
この動画を見る
$(\sqrt 5 - \sqrt 3 )(\sqrt {20} + \sqrt {12} )$
2022愛知県
ざ・息抜き

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{2022}x^{\log_{2022}x}=x^2$の解の積の下3桁を求めよ.
この動画を見る
$\sqrt{2022}x^{\log_{2022}x}=x^2$の解の積の下3桁を求めよ.
福田の入試問題解説〜北海道大学2022年理系第1問〜絶対値の付いた2次関数の最小値(難)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$0 \leqq a \leqq b \leqq 1$を満たすa,bに対し、関数
$f(x)=|x(x-1)|+|(x-a)(x-b)|$
を考える。xが実数の範囲を動くとき、$f(x)$は最小値mをもつとする。
(1)$x \lt 0$および$x \gt 1$では$f(x) \gt m$となることを示せ。
(2)$m=f(0)$または$m=f(1)$であることを示せ。
(3)$a,b$が$0 \leqq a \leqq b \leqq 1$を満たして動くとき、mの最大値を求めよ。
2022北海道大学理系過去問
この動画を見る
$0 \leqq a \leqq b \leqq 1$を満たすa,bに対し、関数
$f(x)=|x(x-1)|+|(x-a)(x-b)|$
を考える。xが実数の範囲を動くとき、$f(x)$は最小値mをもつとする。
(1)$x \lt 0$および$x \gt 1$では$f(x) \gt m$となることを示せ。
(2)$m=f(0)$または$m=f(1)$であることを示せ。
(3)$a,b$が$0 \leqq a \leqq b \leqq 1$を満たして動くとき、mの最大値を求めよ。
2022北海道大学理系過去問
これ解ける?
単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sqrt{ 2022 \sqrt{ 2021 \times 2019 + 1 + 1 } }$
値を求めよ
この動画を見る
$\sqrt{ 2022 \sqrt{ 2021 \times 2019 + 1 + 1 } }$
値を求めよ
大阪大2022

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \alpha=\dfrac{2}{7}\pi$とする.
(1)$ \cos 4\alpha-\cos 3\alpha$を示せ.
(2)$ f(x)=8x^3+4x^2-4x-1,f(\cos \alpha)=0$を示せ.
(3)$ \cos\dfrac{2}{7}\pi$は無理数であることを示せ.
2022阪大過去問
この動画を見る
$ \alpha=\dfrac{2}{7}\pi$とする.
(1)$ \cos 4\alpha-\cos 3\alpha$を示せ.
(2)$ f(x)=8x^3+4x^2-4x-1,f(\cos \alpha)=0$を示せ.
(3)$ \cos\dfrac{2}{7}\pi$は無理数であることを示せ.
2022阪大過去問
令和四年都立国立高校一問目 平方根の計算 2022 入試問題100題解説76問目!

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{\sqrt 5 + \sqrt 3}{\sqrt 2})^2
+(\frac{\sqrt 5 + \sqrt 3}{\sqrt 2})(\frac{\sqrt 5 - \sqrt 3}{\sqrt 2})
-(\frac{\sqrt 5 - \sqrt 3}{\sqrt 2})^2
$
2022都立国立高等学校
この動画を見る
$(\frac{\sqrt 5 + \sqrt 3}{\sqrt 2})^2
+(\frac{\sqrt 5 + \sqrt 3}{\sqrt 2})(\frac{\sqrt 5 - \sqrt 3}{\sqrt 2})
-(\frac{\sqrt 5 - \sqrt 3}{\sqrt 2})^2
$
2022都立国立高等学校
3乗根をはずせ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
3乗根をはずせ.
$\sqrt[3]{8+\sqrt{189}}$
この動画を見る
3乗根をはずせ.
$\sqrt[3]{8+\sqrt{189}}$
2022東海大(医)ドモアブルの定理の基本

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$を解け.
2022東海大(医)過去問
この動画を見る
$(\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$を解け.
2022東海大(医)過去問
小数部分 立教新座 2022 入試問題解説 28問目 西大和学園も全く同じ問題でした。
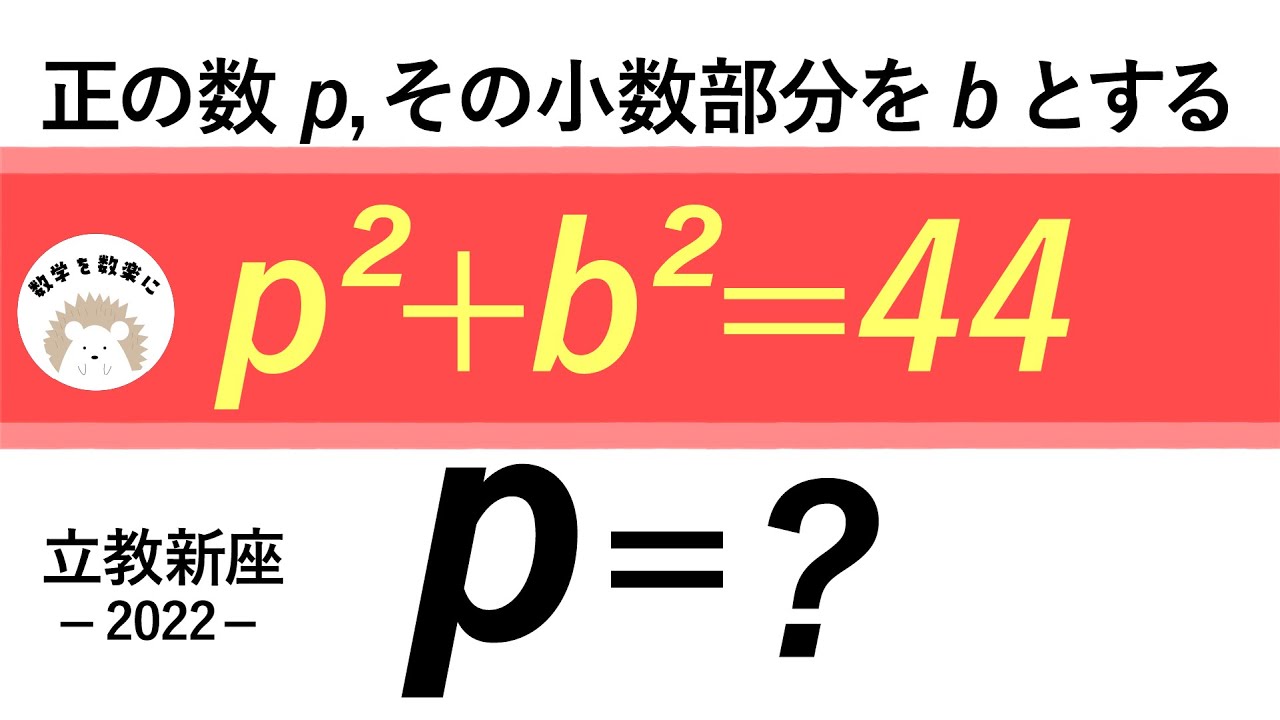
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正の数p、その小数部分をbとする
$p^2+b^2 = 44$
p=?
2022立教新座高等学校
この動画を見る
正の数p、その小数部分をbとする
$p^2+b^2 = 44$
p=?
2022立教新座高等学校
2022乗 昭和学院秀英2022入試問題解説12問目

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 5 + 2)^{2022}(\sqrt 5 -2)^{2020}+(\sqrt 5 +2)^{2020}(\sqrt 5 -2)^{2022}$
2022昭和学院秀英高等学校
この動画を見る
$(\sqrt 5 + 2)^{2022}(\sqrt 5 -2)^{2020}+(\sqrt 5 +2)^{2020}(\sqrt 5 -2)^{2022}$
2022昭和学院秀英高等学校
無理数の2022乗の1の位の数

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(2+\sqrt5)^{2022}$の1の位の数を求めよ.
この動画を見る
$(2+\sqrt5)^{2022}$の1の位の数を求めよ.
基本問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt{2022+a^2+2a}$が整数となる自然数$a$を求めよ.
この動画を見る
$\sqrt{2022+a^2+2a}$が整数となる自然数$a$を求めよ.
