 数と式
数と式
 数と式
数と式
5次方程式
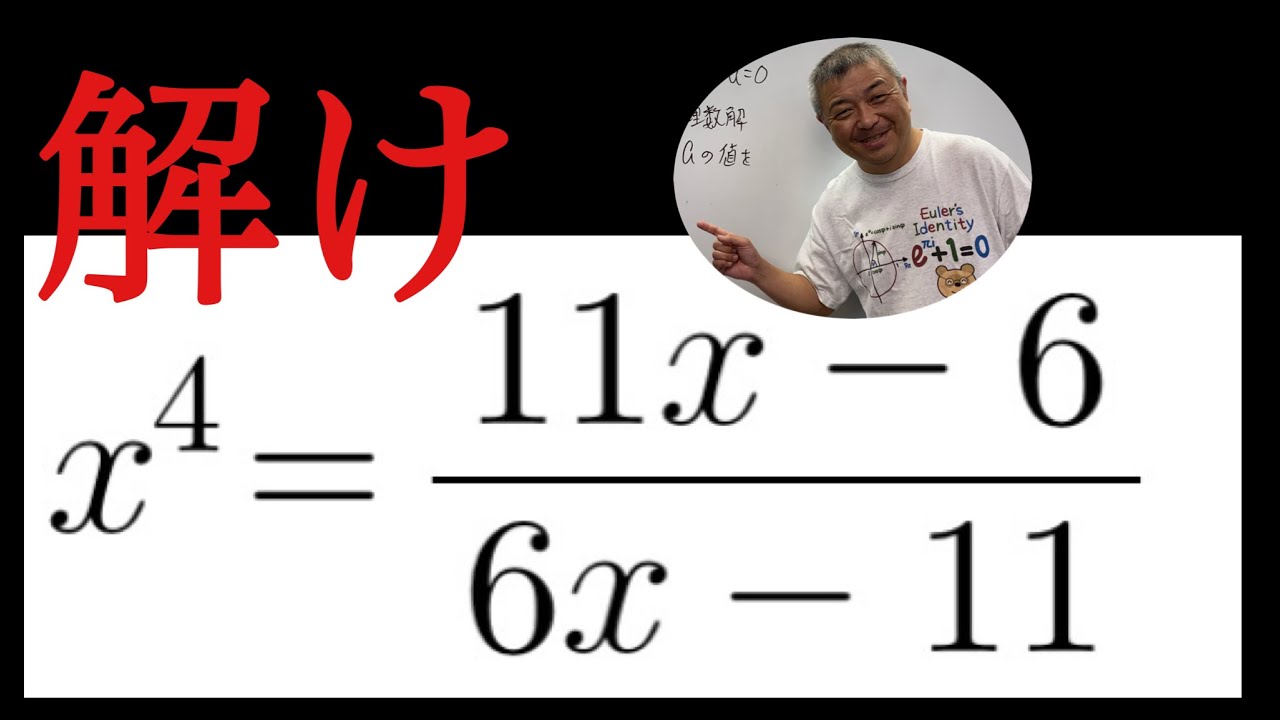
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4=\dfrac{11x^6}{6x-11}$
これを解け.
この動画を見る
$ x^4=\dfrac{11x^6}{6x-11}$
これを解け.
実数とは? 法政大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cの値を求めよ(a,b,c:実数)
$a^2+b^2+c^2=2(-a+c-1)$
法政大学
この動画を見る
a,b,cの値を求めよ(a,b,c:実数)
$a^2+b^2+c^2=2(-a+c-1)$
法政大学
素因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$64000001$を素因数分解すると3つの素因数分解をもつ.
$pqr(p \lt q \lt r)q$の値を求めよ.
この動画を見る
$64000001$を素因数分解すると3つの素因数分解をもつ.
$pqr(p \lt q \lt r)q$の値を求めよ.
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
連立3元3次方程式
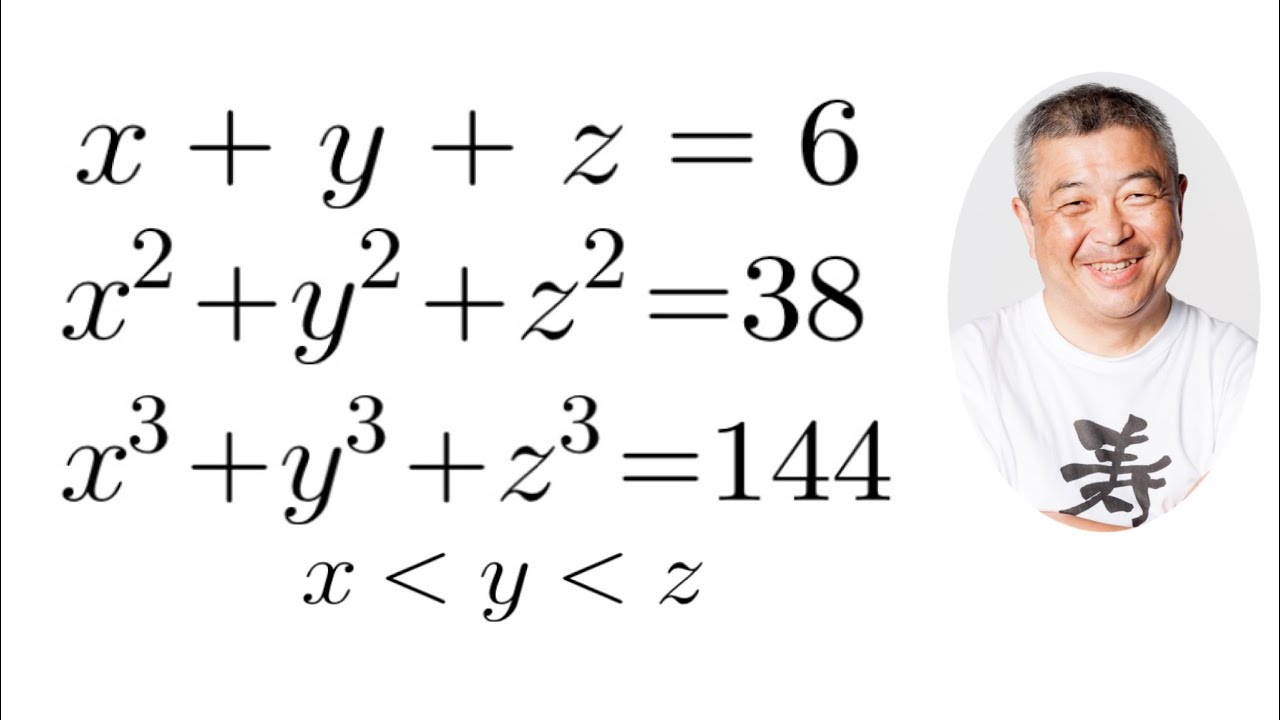
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\lt y\lt z$とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^2+y^2+z^2=38 \\\
x^3+y^3+z^3=144
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$x\lt y\lt z$とする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^2+y^2+z^2=38 \\\
x^3+y^3+z^3=144
\end{array}
\right.
\end{eqnarray}$
二重根号にビビるな! 東京電機大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt x = \sqrt {17 + \sqrt {253}} - \sqrt {17 - \sqrt {253}}$
整数xを求めよ
東京電機大学
この動画を見る
$\sqrt x = \sqrt {17 + \sqrt {253}} - \sqrt {17 - \sqrt {253}}$
整数xを求めよ
東京電機大学
ルートが出てきたら〇〇せよ! 式の値
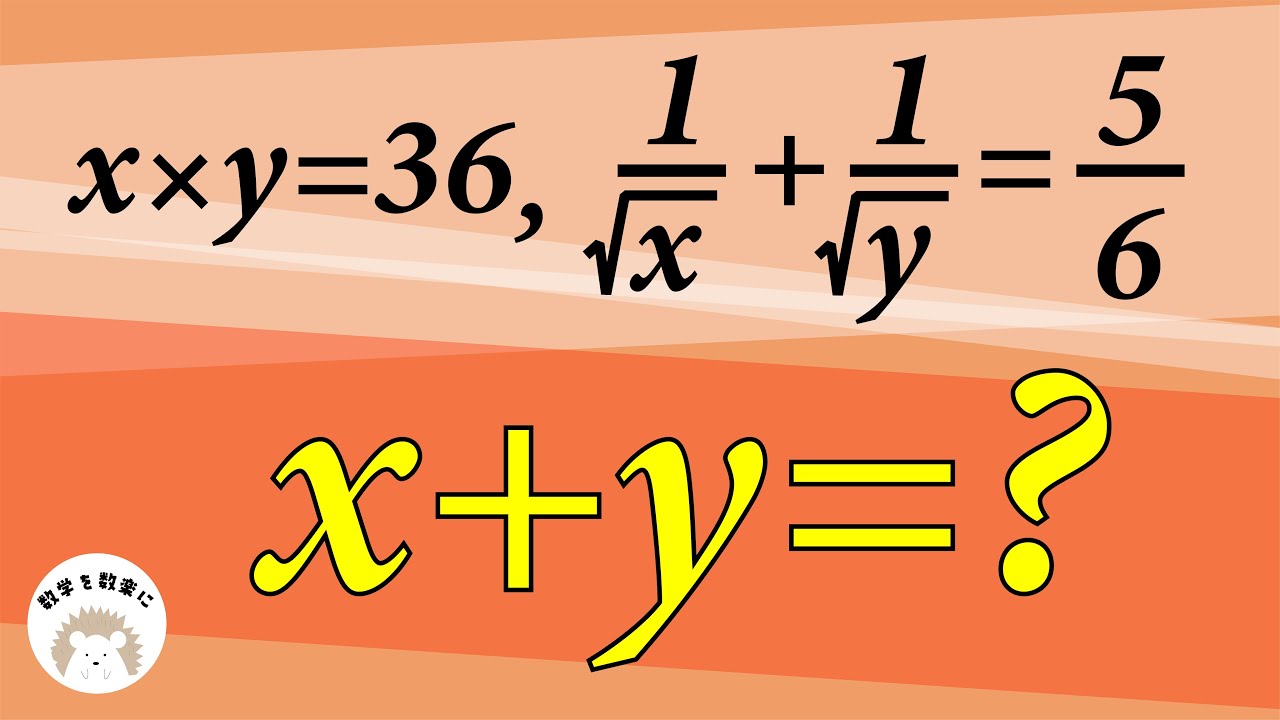
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x \times y = 36$ , $\frac{1}{\sqrt x} + \frac{1}{\sqrt y} = \frac{5}{6}$
$x+y=?$
この動画を見る
$x \times y = 36$ , $\frac{1}{\sqrt x} + \frac{1}{\sqrt y} = \frac{5}{6}$
$x+y=?$
高校範囲の因数分解
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
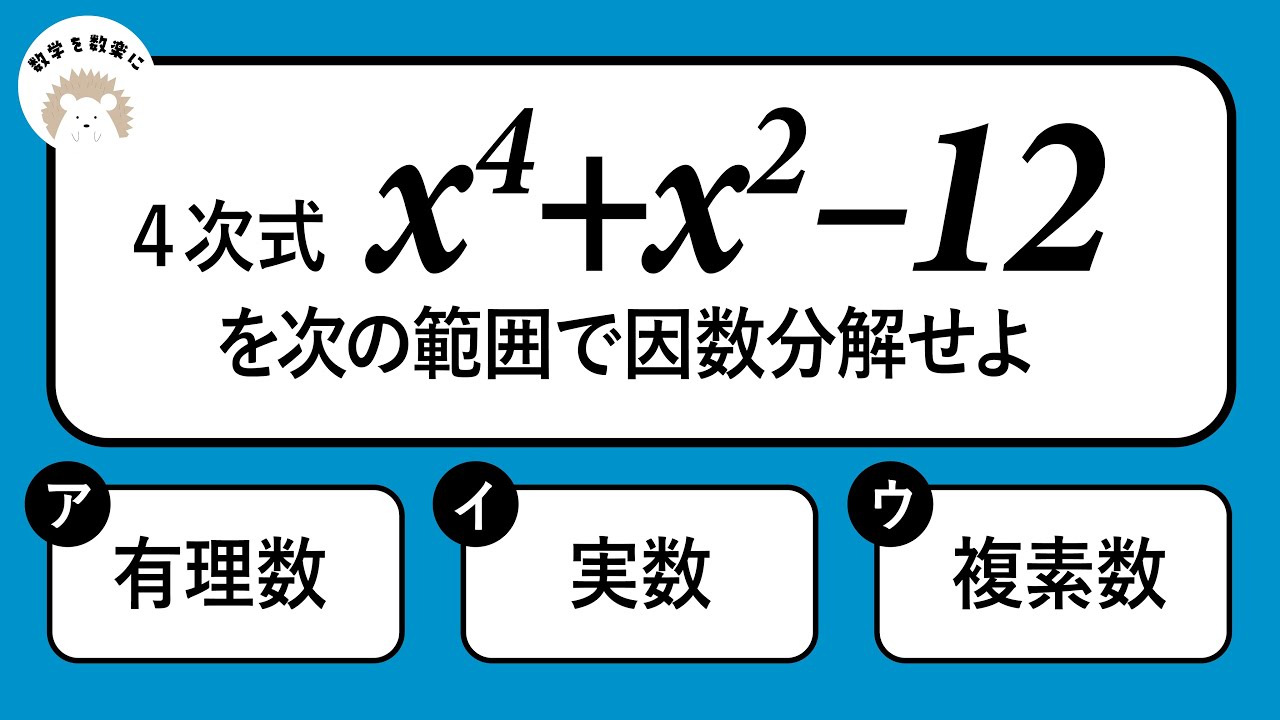
4次式$x^4+x^2-12$を次の範囲で因数分解せよ
㋐有理数
㋑実数
㋒複素数
この動画を見る
4次式$x^4+x^2-12$を次の範囲で因数分解せよ
㋐有理数
㋑実数
㋒複素数
【保存版】絶対値の方程式の裏技

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
絶対値の方程式の裏技紹介動画です
この動画を見る
絶対値の方程式の裏技紹介動画です
式の値 立教大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a-b+c = 1$ , $a^2+b^2+c^2 = 29$のとき
$ac - ab -bc$の値を求めよ
立教大学
この動画を見る
$a-b+c = 1$ , $a^2+b^2+c^2 = 29$のとき
$ac - ab -bc$の値を求めよ
立教大学
福田の数学〜慶應義塾大学2022年商学部第3問〜絶対値の付いた2次関数のグラフと直線の共有点と面積

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{3}}$mを実数とし、関数$y=|x^2-5x+4|$のグラフをC、直線$y=mx$を$l$とする。
(1)グラフCと直線lの共有点の個数は
$\boxed{\ \ アイ\ \ } \lt m \lt \boxed{\ \ ウ\ \ }$のとき0個
$m=\boxed{\ \ エオ\ \ }$のとき1個
$m \lt \boxed{\ \ カキ\ \ },\ m=\boxed{\ \ ク\ \ }$,または$m \gt \boxed{\ \ ケ\ \ }$のとき2個
$m=\boxed{\ \ コ\ \ }$のとき3個
$\boxed{\ \ サ\ \ } \lt m \lt \boxed{\ \ シ\ \ }$のとき4個
以下、グラフCと直線lの共有点の個数が3個の場合を考え、
グラフCと直線lの共有点を、x座標が小さい順にP,Q,Rとする。
(2)3点P,Q,Rのx座標は、順に$\boxed{\ \ ス\ \ }-\sqrt{\boxed{\ \ セ\ \ }},\ \boxed{\ \ ソ\ \ },\ \boxed{\ \ タ\ \ }+\sqrt{\boxed{\ \ チ\ \ }}$である。
(3)グラフCと線分QRで囲まれた部分の面積は$\frac{-\ \boxed{\ \ ツ\ \ }+\boxed{\ \ テト\ \ }\sqrt{\boxed{\ \ ナ\ \ }}}{\boxed{\ \ ニ\ \ }}$である。
2022慶應義塾大学商学部過去問
5乗数を平方の和で
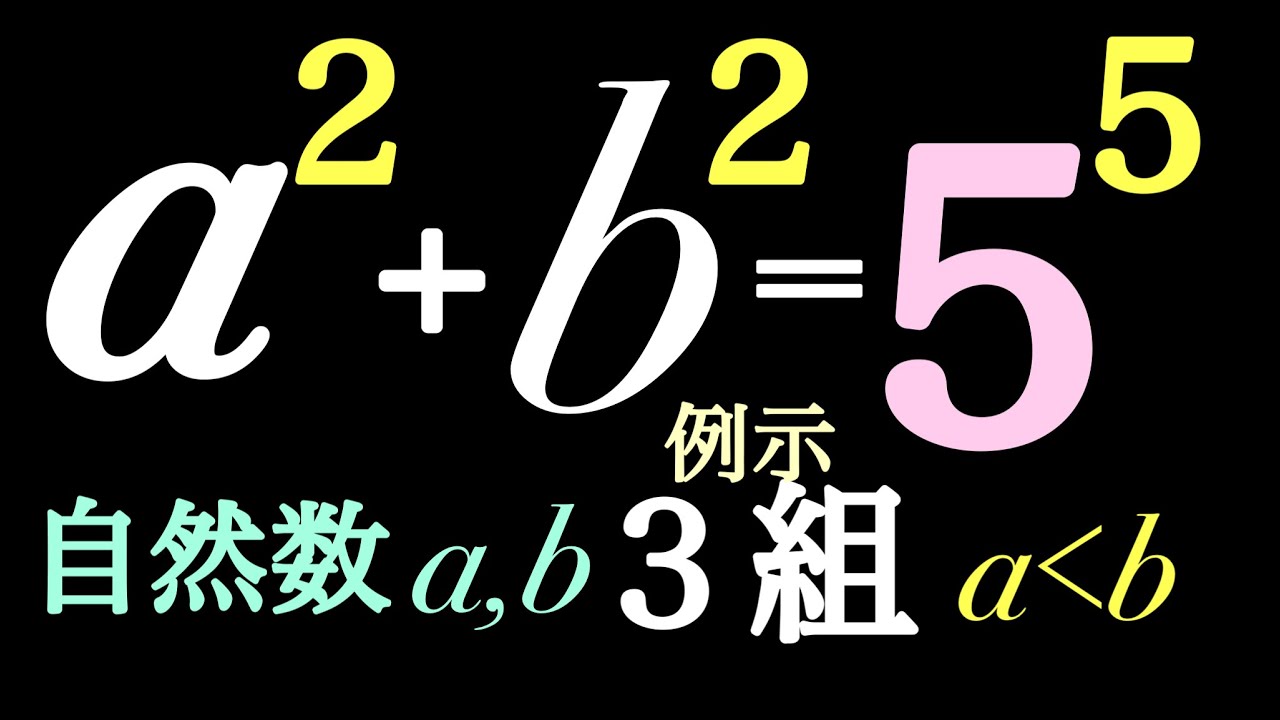
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2+b^2=5^5$,$a\lt b$
自然数$(a,b)$を3組例示せよ.
この動画を見る
$a^2+b^2=5^5$,$a\lt b$
自然数$(a,b)$を3組例示せよ.
福田の数学〜慶應義塾大学2022年商学部第1問(1)〜倍数の個数を数える

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
ただの計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{101^2+101^2・102^2+102^2}$
これを計算せよ.
この動画を見る
$ \sqrt{101^2+101^2・102^2+102^2}$
これを計算せよ.
正しいか、正しくないか

式の値 筑波大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
実数a,b,c,dが4つの等式
$a^2+b^2 = 1$ , $c^2+d^2 = 1$ ,
$ac +bd = 0$ , $ad +bc = 0 $を満たすとき
積abcdを求めよ
筑波大学
この動画を見る
実数a,b,c,dが4つの等式
$a^2+b^2 = 1$ , $c^2+d^2 = 1$ ,
$ac +bd = 0$ , $ad +bc = 0 $を満たすとき
積abcdを求めよ
筑波大学
破れたページは何ページ目?

単元:
#数Ⅰ#数と式#2次関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1枚だけページが破れた本があります。
破れていないページの番号を合計すると15000になる
破れたページは何ページ目ですか?
この動画を見る
1枚だけページが破れた本があります。
破れていないページの番号を合計すると15000になる
破れたページは何ページ目ですか?
【無理数とは!】平方根(有理数と無理数)後編:教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根(有理数と無理数)に関して解説していきます.
この動画を見る
平方根(有理数と無理数)に関して解説していきます.
4次式の因数分解

【用語の違いは何!?】苦手な人が多い有理数と無理数、有限小数、循環小数の違いを簡単に解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
中学3年生 数学
有理数と無理数、有限小数、循環小数の違いについて解説します。
この動画を見る
中学3年生 数学
有理数と無理数、有限小数、循環小数の違いについて解説します。
【有理数とは!】平方根(有理数と無理数)前編:教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根(有理数と無理数)に関して解説していきます.
この動画を見る
平方根(有理数と無理数)に関して解説していきます.
福田の入試問題解説〜慶應義塾大学2022年医学部第1問(3)〜集合と対数不等式

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)関数$f(x)=\log_{\frac{1}{3}}\sqrt{3x^3-2x^2}$と$g(x)=\log_9(3x^2-2)$の定義域をそれぞれ
集合A,Bで表すと、$A\cap B=\left\{x|xはx \gt \boxed{\ \ オ\ \ }$を満たす実数である。
実数xが集合$A\cap B$の要素であるとき、$f(x)+g(x) \lt 0$となるための条件は
$\boxed{\ \ オ\ \ } \lt x \lt \boxed{\ \ カ\ \ }$または$x \gt \boxed{\ \ キ\ \ }$となることである。
2022慶應義塾大学医学部過去問
この動画を見る
(3)関数$f(x)=\log_{\frac{1}{3}}\sqrt{3x^3-2x^2}$と$g(x)=\log_9(3x^2-2)$の定義域をそれぞれ
集合A,Bで表すと、$A\cap B=\left\{x|xはx \gt \boxed{\ \ オ\ \ }$を満たす実数である。
実数xが集合$A\cap B$の要素であるとき、$f(x)+g(x) \lt 0$となるための条件は
$\boxed{\ \ オ\ \ } \lt x \lt \boxed{\ \ カ\ \ }$または$x \gt \boxed{\ \ キ\ \ }$となることである。
2022慶應義塾大学医学部過去問
3通りで解説 分母の有理化
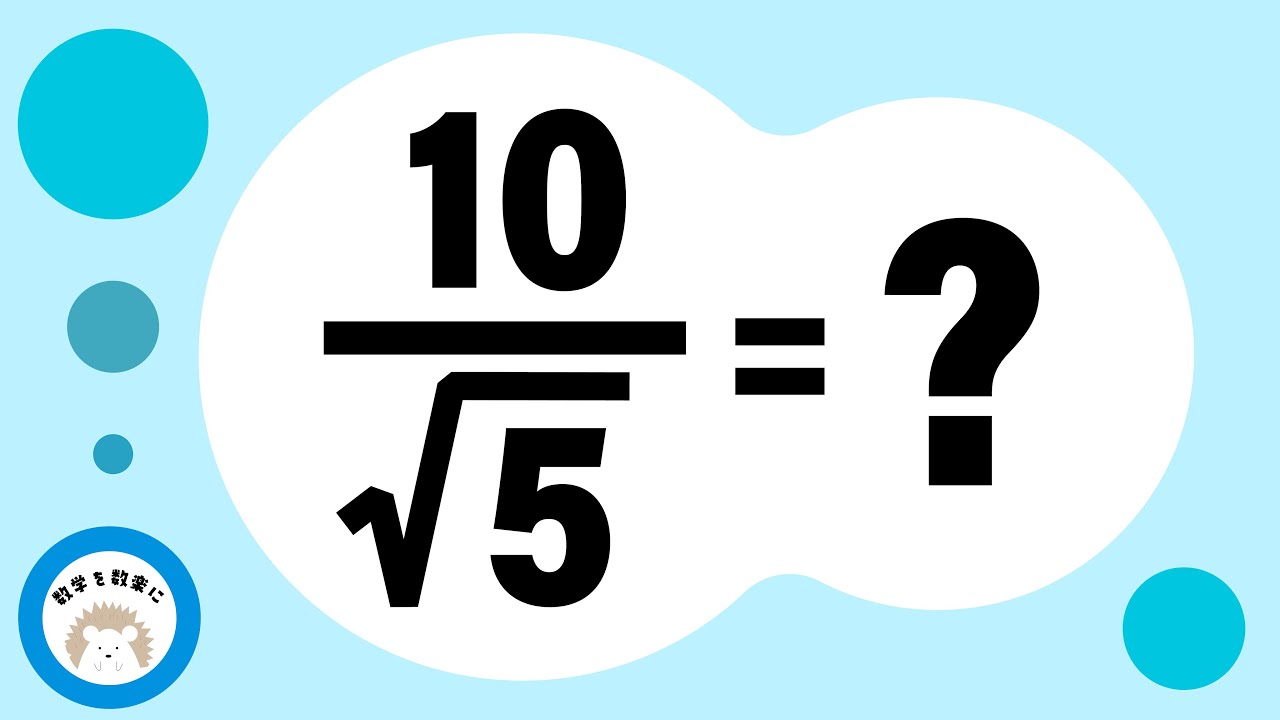
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{10}{\sqrt 5} = ?$
この動画を見る
$\frac{10}{\sqrt 5} = ?$
福田の入試問題解説〜慶應義塾大学2022年医学部第1問(2)〜高次式の因数分解

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)整式$x^5+x^4+x^3+x^2+x+1$は、整数を係数とし、次数が1以上で、
かつ最高次の項の係数が1であるような3つの整式$\boxed{\ \ イ\ \ },\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ }$の積に
因数分解せよ。
2022慶應義塾大学医学部過去問
この動画を見る
(2)整式$x^5+x^4+x^3+x^2+x+1$は、整数を係数とし、次数が1以上で、
かつ最高次の項の係数が1であるような3つの整式$\boxed{\ \ イ\ \ },\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ }$の積に
因数分解せよ。
2022慶應義塾大学医学部過去問
福田の入試問題解説〜慶應義塾大学2022年医学部第1問(1)〜絶対値の付いた方程式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1)方程式$4||x|-1|=x+2$の解を全て求めると$x=\boxed{\ \ あ\ \ }$ となる。
2022慶應義塾大学医学部過去問
この動画を見る
(1)方程式$4||x|-1|=x+2$の解を全て求めると$x=\boxed{\ \ あ\ \ }$ となる。
2022慶應義塾大学医学部過去問
The 因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (a+b-2ab)(a+b-2)+(1-ab)^2$
これを因数分解せよ.
この動画を見る
$ (a+b-2ab)(a+b-2)+(1-ab)^2$
これを因数分解せよ.
式の値 最後に落とし穴!? 福岡大学
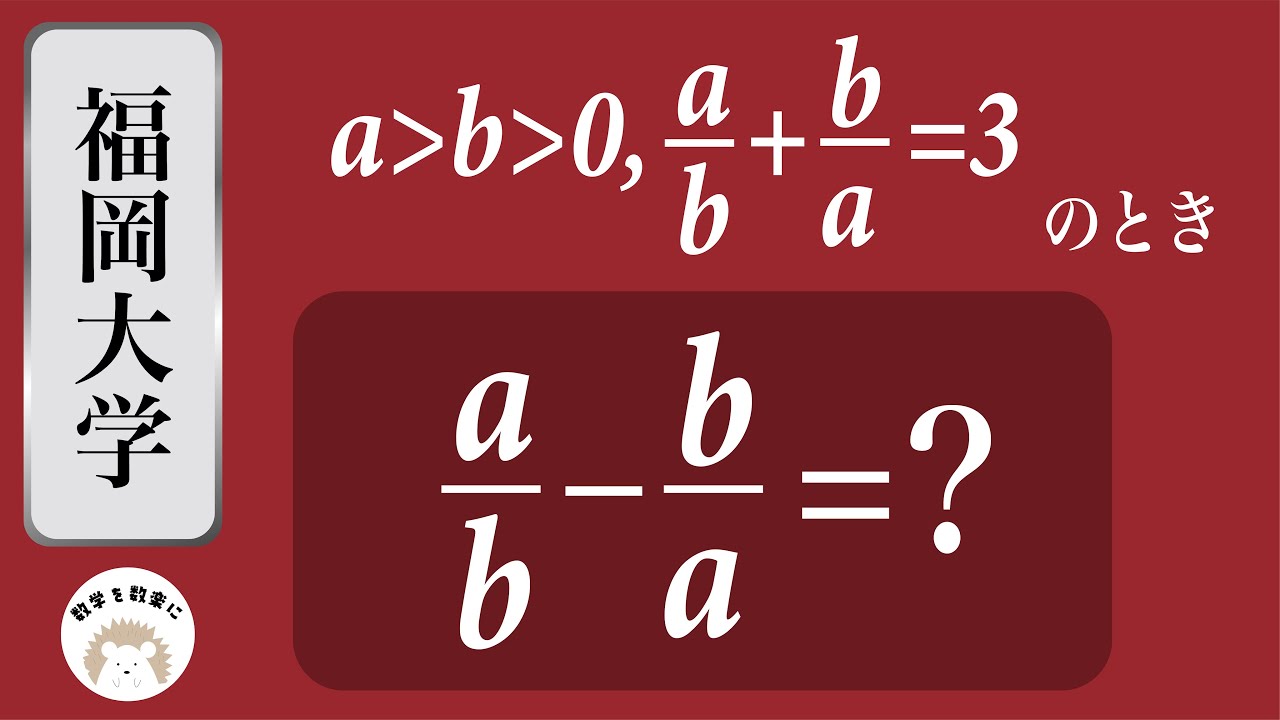
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a>b>0$ , $\frac{a}{b}+\frac{b}{a} = 3$のとき
$\frac{a}{b} - \frac{b}{a} =?$
福岡大学
この動画を見る
$a>b>0$ , $\frac{a}{b}+\frac{b}{a} = 3$のとき
$\frac{a}{b} - \frac{b}{a} =?$
福岡大学
ただの4次方程式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ (3x+1)(4x+1)(6x+1)(12x+1)=2$
これを解け.
この動画を見る
$ (3x+1)(4x+1)(6x+1)(12x+1)=2$
これを解け.
因数分解しようぜ!

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3+(x^2-3x+4)^2+2$
これを因数分解せよ.
この動画を見る
$ x^3+(x^2-3x+4)^2+2$
これを因数分解せよ.
等式の変形 西大和学園

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
aについて解け
$\frac{1}{a}+\frac{2}{b} = \frac{1}{ca}$
2022西大和学園高等学校
この動画を見る
aについて解け
$\frac{1}{a}+\frac{2}{b} = \frac{1}{ca}$
2022西大和学園高等学校
