 数と式
数と式
 数と式
数と式
高校範囲?と思わせる慶應義塾高校の問題

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c= \frac{1}{3}$ , $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$のとき
(a-1)(b-1)(c-1)=
慶應義塾高等学校
この動画を見る
$a+b+c= \frac{1}{3}$ , $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$のとき
(a-1)(b-1)(c-1)=
慶應義塾高等学校
ざ・挟み撃ち

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{\sqrt{n^4+1}}+\dfrac{2}{\sqrt{n^4+2}}+・・・・・・+\dfrac{n}{\sqrt{n^4+n}}$
$\displaystyle \lim_{n\to \infty} \displaystyle \sum_{k=1}^{n}\dfrac{k}{\sqrt{n^4+k}}$
$a_n=\displaystyle \sum_{k=1}^n \dfrac{n}{\sqrt{k}}$
$b_n=\displaystyle \sum_{k=1}^n \dfrac{1}{\sqrt{2k+1}}$
$\displaystyle \lim_{n\to \infty} a_n,\displaystyle \lim_{n\to \infty}\dfrac{bn}{an}$を求めよ.
東大1990過去問
この動画を見る
$\dfrac{1}{\sqrt{n^4+1}}+\dfrac{2}{\sqrt{n^4+2}}+・・・・・・+\dfrac{n}{\sqrt{n^4+n}}$
$\displaystyle \lim_{n\to \infty} \displaystyle \sum_{k=1}^{n}\dfrac{k}{\sqrt{n^4+k}}$
$a_n=\displaystyle \sum_{k=1}^n \dfrac{n}{\sqrt{k}}$
$b_n=\displaystyle \sum_{k=1}^n \dfrac{1}{\sqrt{2k+1}}$
$\displaystyle \lim_{n\to \infty} a_n,\displaystyle \lim_{n\to \infty}\dfrac{bn}{an}$を求めよ.
東大1990過去問
【裏技】こんな因数分解あり?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x^2-24x+60$ を因数分解せよ
因数分解の解き方解説動画です
この動画を見る
$x^2-24x+60$ を因数分解せよ
因数分解の解き方解説動画です
因数分解の全パターン③【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の式を因数分解せよ。
(1)$2x^2-10xy-48y^2$
(2)$a^3+27b^3$
(3)$x^3+3x^2+3x+1$
(4)$(x^2-3x)(x^2-3x-2)-8$
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(7)$x^2+5xy+5x+6y^2+11y+4$
(8)$2x^2-3xy-2y^2+x+3y-1$
(9)$x^4-5x^2+4$
(10)$x^4+x^2+1$
(11)$x^4-6x^2+1$
(12)$(x+1)(x+3)(x+5)(x+7)+15$
(13)$(a+b)c^2+(b+c)a^2+(c+a)b^2+2abc$
(14)$x^3+y^3+z^3-3xyz$
この動画を見る
次の式を因数分解せよ。
(1)$2x^2-10xy-48y^2$
(2)$a^3+27b^3$
(3)$x^3+3x^2+3x+1$
(4)$(x^2-3x)(x^2-3x-2)-8$
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(7)$x^2+5xy+5x+6y^2+11y+4$
(8)$2x^2-3xy-2y^2+x+3y-1$
(9)$x^4-5x^2+4$
(10)$x^4+x^2+1$
(11)$x^4-6x^2+1$
(12)$(x+1)(x+3)(x+5)(x+7)+15$
(13)$(a+b)c^2+(b+c)a^2+(c+a)b^2+2abc$
(14)$x^3+y^3+z^3-3xyz$
【中学数学】因数分解のテクニック~マル秘必殺技~ 3-3【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の式を因数分解せよ
$x^2-24x+60$
この動画を見る
次の式を因数分解せよ
$x^2-24x+60$
【中学数学】ルートの問題演習~代入する問題のテクニック~ 2-11【中3数学】

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x=2-\sqrt{3}$のとき、$x^2-4x-1$の値を求めよ
この動画を見る
$x=2-\sqrt{3}$のとき、$x^2-4x-1$の値を求めよ
暗算でも出せるかな?早くも2022問題。x^2022+x^-2022の値
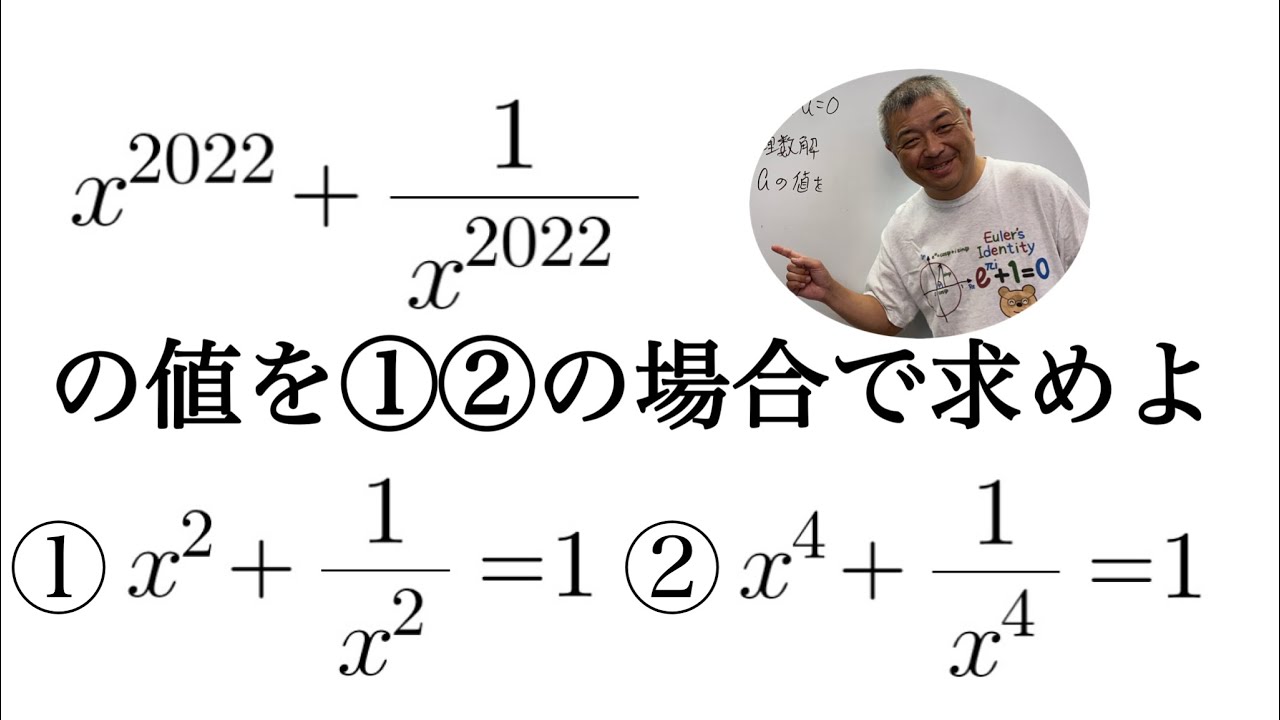
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$x^2+\dfrac{1}{x^2}=1$
②$x^4+\dfrac{1}{x^4}=1$
それぞれ$x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
この動画を見る
①$x^2+\dfrac{1}{x^2}=1$
②$x^4+\dfrac{1}{x^4}=1$
それぞれ$x^{2022}+\dfrac{1}{x^{2022}}$の値を求めよ.
スッキリだそう
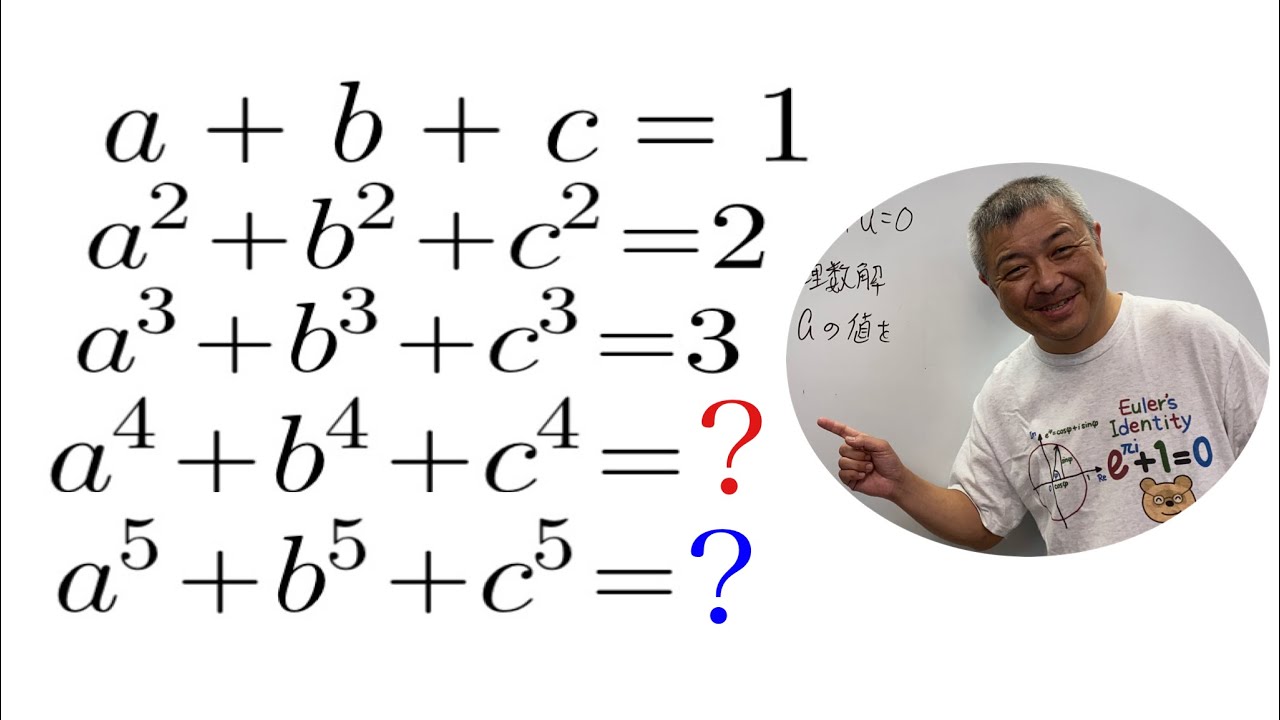
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a+b+c=1$
$a^2+b^2+c^2=2$
$a^3+b^3+c^3=3$
$a^4+b^4+c^4=\Box$
$a^5*b^5+c^5=\Box$
$\Box$を求めよ.
この動画を見る
$a+b+c=1$
$a^2+b^2+c^2=2$
$a^3+b^3+c^3=3$
$a^4+b^4+c^4=\Box$
$a^5*b^5+c^5=\Box$
$\Box$を求めよ.
【数Ⅰ】数と式:複2次式の因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を因数分解しよう。
(1)$x^4+x^2+1$
(2)$x^4+4x^2+16$
この動画を見る
次の式を因数分解しよう。
(1)$x^4+x^2+1$
(2)$x^4+4x^2+16$
福田の数学〜上智大学2021年TEAP利用理系第2問〜集合の要素と包含関係

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#集合と命題(集合・命題と条件・背理法)#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$実数からなる集合A,B,Cを次のように定義する。ただし、$a \gt 0$
$A=\left\{x |\ |x| \lt a \right\}$
$B=\left\{x |\ (x+2)(x-5)(x^2+2x-7) \leqq 0 \right\}$
$C=\left\{x |\ 3^{\frac{x}{3}} \leqq \frac{1}{3}(x+4) \right\}$
(1)$A \cap B$が空集合であるための必要十分条件は$a \boxed{\ \ お\ \ } \ \boxed{\ \ \alpha\ \ }$である。
(2)$A \supset B$であるための必要十分条件は$a \boxed{\ \ か\ \ } \ \boxed{\ \ \beta\ \ }$である。
$\boxed{\ \ お\ \ },\ \boxed{\ \ か\ \ }$の選択肢$:(\textrm{a})= (\textrm{b})\lt (\textrm{c})\leqq (\textrm{d})\gt (\textrm{e})\geqq (\textrm{f})\neq$
$\boxed{\ \ \alpha\ \ },\ \boxed{\ \ \beta\ \ }$の選択肢$:(\textrm{a})1 (\textrm{b})2 (\textrm{c})3 (\textrm{d})5 (\textrm{e})7 (\textrm{f})10$
($\textrm{g})-1+2\sqrt2 (\textrm{h})1+2\sqrt2 (\textrm{i})-2+\sqrt7 (\textrm{j})2+\sqrt7$
(3)$-1 \boxed{\ \ き\ \ }C$であり、$5 \boxed{\ \ く\ \ }C$である。
$\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ }$の選択肢$:(\textrm{a})\in (\textrm{b})\notin (\textrm{c})\ni (\textrm{d})∋ (\textrm{e})= (\textrm{f})\subset (\textrm{g})\supset$
(4)Cに属する整数は$\boxed{\ \ オ\ \ }$個ある。
(5)$A \subset C$となるaのうち、整数で最大のものは$\boxed{\ \ カ\ \ }$である。
(6)$A \supset C$となるaのうち、整数で最小のものは$\boxed{\ \ キ\ \ }$である。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{2}}$実数からなる集合A,B,Cを次のように定義する。ただし、$a \gt 0$
$A=\left\{x |\ |x| \lt a \right\}$
$B=\left\{x |\ (x+2)(x-5)(x^2+2x-7) \leqq 0 \right\}$
$C=\left\{x |\ 3^{\frac{x}{3}} \leqq \frac{1}{3}(x+4) \right\}$
(1)$A \cap B$が空集合であるための必要十分条件は$a \boxed{\ \ お\ \ } \ \boxed{\ \ \alpha\ \ }$である。
(2)$A \supset B$であるための必要十分条件は$a \boxed{\ \ か\ \ } \ \boxed{\ \ \beta\ \ }$である。
$\boxed{\ \ お\ \ },\ \boxed{\ \ か\ \ }$の選択肢$:(\textrm{a})= (\textrm{b})\lt (\textrm{c})\leqq (\textrm{d})\gt (\textrm{e})\geqq (\textrm{f})\neq$
$\boxed{\ \ \alpha\ \ },\ \boxed{\ \ \beta\ \ }$の選択肢$:(\textrm{a})1 (\textrm{b})2 (\textrm{c})3 (\textrm{d})5 (\textrm{e})7 (\textrm{f})10$
($\textrm{g})-1+2\sqrt2 (\textrm{h})1+2\sqrt2 (\textrm{i})-2+\sqrt7 (\textrm{j})2+\sqrt7$
(3)$-1 \boxed{\ \ き\ \ }C$であり、$5 \boxed{\ \ く\ \ }C$である。
$\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ }$の選択肢$:(\textrm{a})\in (\textrm{b})\notin (\textrm{c})\ni (\textrm{d})∋ (\textrm{e})= (\textrm{f})\subset (\textrm{g})\supset$
(4)Cに属する整数は$\boxed{\ \ オ\ \ }$個ある。
(5)$A \subset C$となるaのうち、整数で最大のものは$\boxed{\ \ カ\ \ }$である。
(6)$A \supset C$となるaのうち、整数で最小のものは$\boxed{\ \ キ\ \ }$である。
2021上智大学理系過去問
1996 平成8年 大阪府

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
▢内に+-×÷のいずれかの記号を入れる。(同じ記号は何度使ってもよい)
$\sqrt{1▢9▢9▢6} =8$
1991大阪府
この動画を見る
▢内に+-×÷のいずれかの記号を入れる。(同じ記号は何度使ってもよい)
$\sqrt{1▢9▢9▢6} =8$
1991大阪府
【数Ⅰ】数と式:因数分解:a³+b³+c³-3abcの因数分解の利用

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$を用いて、次の式を因数分解しよう。
$x^3+y^3-1+3xy$
この動画を見る
$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$を用いて、次の式を因数分解しよう。
$x^3+y^3-1+3xy$
【数I】中高一貫校問題集3(数式・関数編)6:数と式:多項式:整式の減法の注意点
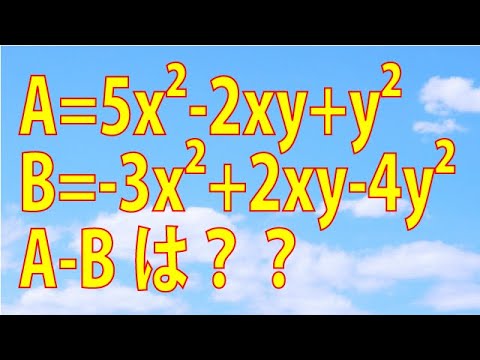
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A=5x²-2xy+y²、B=-3x²+2xy-4y²であるとき、A-Bを計算しよう。
この動画を見る
A=5x²-2xy+y²、B=-3x²+2xy-4y²であるとき、A-Bを計算しよう。
【数Ⅰ】数と式:整式の加法と減法:整理してから代入する
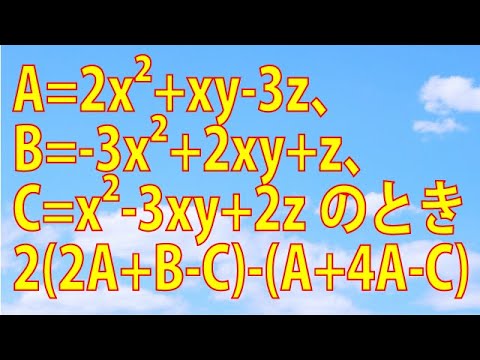
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$A=2x^2+xy-3z、B=-3x^2+2xy+z、C=x^2-3xy+2z$であるとき、$2(2A+B-C)-(A+4A-C)$を計算しよう。
この動画を見る
$A=2x^2+xy-3z、B=-3x^2+2xy+z、C=x^2-3xy+2z$であるとき、$2(2A+B-C)-(A+4A-C)$を計算しよう。
福田の数学〜上智大学2021年TEAP利用文系第4問(1)〜条件の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$(1)関数$f(x)$に対する以下の条件(P)を考える。
$(P): f(x) \gt 3$を満たす5以上の自然数nが存在する。
条件(P)の否定として正しいものを以下の選択肢からすべて選べ。
$(\textrm{a})f(n) \leqq 3$を満たす5以上の自然数nが存在する。
$(\textrm{b})f(n) \gt 3$を満たす5未満の自然数nが存在する。
$(\textrm{c})f(n) \leqq 3$を満たす5未満の自然数nが存在する。
$(\textrm{d})n$が5以上の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{e})n$が5未満の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{f})n$が5未満の自然数ならば$f(n) \gt 3$が成り立つ。
$(\textrm{g})f(n) \gt 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{h})f(n) \leqq 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{i})f(n) \leqq 3$が5未満の全ての自然数nに対して成り立つ。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{4}}$(1)関数$f(x)$に対する以下の条件(P)を考える。
$(P): f(x) \gt 3$を満たす5以上の自然数nが存在する。
条件(P)の否定として正しいものを以下の選択肢からすべて選べ。
$(\textrm{a})f(n) \leqq 3$を満たす5以上の自然数nが存在する。
$(\textrm{b})f(n) \gt 3$を満たす5未満の自然数nが存在する。
$(\textrm{c})f(n) \leqq 3$を満たす5未満の自然数nが存在する。
$(\textrm{d})n$が5以上の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{e})n$が5未満の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{f})n$が5未満の自然数ならば$f(n) \gt 3$が成り立つ。
$(\textrm{g})f(n) \gt 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{h})f(n) \leqq 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{i})f(n) \leqq 3$が5未満の全ての自然数nに対して成り立つ。
2021上智大学文系過去問
【数I】中高一貫校用問題集(数式・関数編)数と式:多項式:整式の減法の注意点
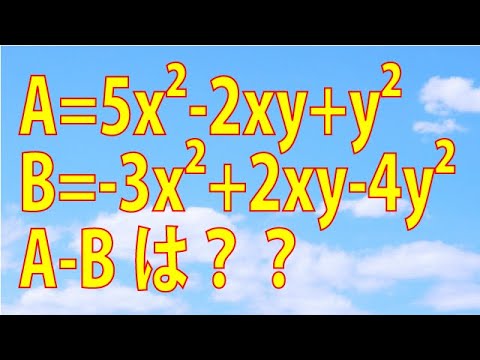
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#数Ⅰ#数Ⅱ#数と式#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$A=5x^2-2xy+y^2、B=-3x^2+2xy-4y^2$であるとき、$A-B$を計算しよう。
この動画を見る
$A=5x^2-2xy+y^2、B=-3x^2+2xy-4y^2$であるとき、$A-B$を計算しよう。
素因数分解3200021

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
素因数分解せよ.
$3200021$
ただし,素因数は3つである.
この動画を見る
素因数分解せよ.
$3200021$
ただし,素因数は3つである.
【数Ⅰ】中高一貫校問題集3(論理・確率編)10:集合と命題:集合:要素の決定

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A={2,4,x-1},B={3,2x-y-1},C={2,2x+z-2}とする。
B⊂A、B=Cが成り立つとき、x,y,zの値を求めよう。
この動画を見る
A={2,4,x-1},B={3,2x-y-1},C={2,2x+z-2}とする。
B⊂A、B=Cが成り立つとき、x,y,zの値を求めよう。
【数Ⅰ】中高一貫校用問題集(論理・確率編)集合と命題:集合:要素の決定

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$A={2,4,x-1},B={3,2x-y-1},C={2,2x+z-2}$とする。
$B⊂A、B=C$が成り立つとき、x,y,zの値を求めよう。
この動画を見る
$A={2,4,x-1},B={3,2x-y-1},C={2,2x+z-2}$とする。
$B⊂A、B=C$が成り立つとき、x,y,zの値を求めよう。
千葉大 ドゥモアブルの定理

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\pi$
①$\alpha^6+\alpha^5+\alpha^4+\alpha^3+\alpha^2+\alpha$の値を求めよ.
②$(1-\alpha)(1-\alpha^2)(1-\alpha^3)\times(1-\alpha^4)(1-\alpha^5)$
$(1-\alpha^6)$の値を求めよ.
千葉大過去問
この動画を見る
$\alpha=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\pi$
①$\alpha^6+\alpha^5+\alpha^4+\alpha^3+\alpha^2+\alpha$の値を求めよ.
②$(1-\alpha)(1-\alpha^2)(1-\alpha^3)\times(1-\alpha^4)(1-\alpha^5)$
$(1-\alpha^6)$の値を求めよ.
千葉大過去問
早くも2022問題。視聴者が類題を作ってくれました

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を
$(x^{16}+1)(x^8+1)(x^4+1)(x^2+1)(x+1)$で割った余りを求めよ.
この動画を見る
$x^{2022}$を
$(x^{16}+1)(x^8+1)(x^4+1)(x^2+1)(x+1)$で割った余りを求めよ.
山梨大(医)整式の剰余

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2020}$を$x^2-x+1$で割った余りを求めよ.
2020山梨大(医)過去問
この動画を見る
$x^{2020}$を$x^2-x+1$で割った余りを求めよ.
2020山梨大(医)過去問
福田の数学〜上智大学2021年理工学部第2問(1)〜条件を満たす関数と命題の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)実数全体で定義され、実数の値をとる関数$f(x)$に対する次の条件$p$を考える。
$p:「K以上の全ての実数xに対してf(x) \geqq 1」$が成り立つような実数Kが存在する。
$(\textrm{i})$次に挙げた関数$(\textrm{a})~(\textrm{d})$のそれぞれについて、pを満たすならばo、pを
満たさないならばxをマークせよ。
$(\textrm{a})f(x)=xe^{-x} (\textrm{b})f(x)=\frac{2x^2+1}{x^2+1} (\textrm{c})f(x)=x+\sin x (\textrm{d})f(x)=x\sin x$
$(\textrm{ii})$次の条件がpの否定になるように、$\boxed{\ \ あ\ \ }~\boxed{\ \ え\ \ }$のそれぞれの選択肢から、
あてはまるものを選べ。
・$「\boxed{\ \ あ\ \ }\ \boxed{\ \ い\ \ }$実数に対して$\boxed{\ \ う\ \ }」が\boxed{\ \ え\ \ }$
$\boxed{\ \ あ\ \ }$の選択肢$:(\textrm{a})K$以上の $(\textrm{b})K$未満の
$\boxed{\ \ い\ \ }$の選択肢:$(\textrm{a})$すべての $(\textrm{b})$ある
$\boxed{\ \ う\ \ }$の選択肢$:(\textrm{a})f(x) \geqq 1 (\textrm{b})f(x) \lt 1$
$\boxed{\ \ え\ \ }$の選択肢$:(\textrm{a})$どんな実数Kについても成り立つ $\\(\textrm{b})$成り立つような実数Kが存在する
$(\textrm{iii})$関数$f(x)$に対して、$g(x)=2f(x)$で関数$g(x)$を定める。次に挙げた命題$(\textrm{A})~(\textrm{D})$
のそれぞれについて、正しければoを、正しくなければxを、マークせよ。
$(\textrm{A})f(x)$が$p$を満たすならば、$g(x)$も$p$を満たす。
$(\textrm{B})g(x)$が$p$を満たすならば、$f(x)$もpを満たす。
$(\textrm{C})f(x)$が$p$を満たさないならば、$g(x)$もpを満たさない。
$(\textrm{D})f(x)$がpを満たさないならば、$g(x)$も$p$を満たす。
2021上智大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$(1)実数全体で定義され、実数の値をとる関数$f(x)$に対する次の条件$p$を考える。
$p:「K以上の全ての実数xに対してf(x) \geqq 1」$が成り立つような実数Kが存在する。
$(\textrm{i})$次に挙げた関数$(\textrm{a})~(\textrm{d})$のそれぞれについて、pを満たすならばo、pを
満たさないならばxをマークせよ。
$(\textrm{a})f(x)=xe^{-x} (\textrm{b})f(x)=\frac{2x^2+1}{x^2+1} (\textrm{c})f(x)=x+\sin x (\textrm{d})f(x)=x\sin x$
$(\textrm{ii})$次の条件がpの否定になるように、$\boxed{\ \ あ\ \ }~\boxed{\ \ え\ \ }$のそれぞれの選択肢から、
あてはまるものを選べ。
・$「\boxed{\ \ あ\ \ }\ \boxed{\ \ い\ \ }$実数に対して$\boxed{\ \ う\ \ }」が\boxed{\ \ え\ \ }$
$\boxed{\ \ あ\ \ }$の選択肢$:(\textrm{a})K$以上の $(\textrm{b})K$未満の
$\boxed{\ \ い\ \ }$の選択肢:$(\textrm{a})$すべての $(\textrm{b})$ある
$\boxed{\ \ う\ \ }$の選択肢$:(\textrm{a})f(x) \geqq 1 (\textrm{b})f(x) \lt 1$
$\boxed{\ \ え\ \ }$の選択肢$:(\textrm{a})$どんな実数Kについても成り立つ $\\(\textrm{b})$成り立つような実数Kが存在する
$(\textrm{iii})$関数$f(x)$に対して、$g(x)=2f(x)$で関数$g(x)$を定める。次に挙げた命題$(\textrm{A})~(\textrm{D})$
のそれぞれについて、正しければoを、正しくなければxを、マークせよ。
$(\textrm{A})f(x)$が$p$を満たすならば、$g(x)$も$p$を満たす。
$(\textrm{B})g(x)$が$p$を満たすならば、$f(x)$もpを満たす。
$(\textrm{C})f(x)$が$p$を満たさないならば、$g(x)$もpを満たさない。
$(\textrm{D})f(x)$がpを満たさないならば、$g(x)$も$p$を満たす。
2021上智大学理工学部過去問
等式の変形 智弁和歌山

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xについて解け
$\frac{1}{x} - \frac{2}{xy} = 3y$
智弁学園和歌山高等学校
この動画を見る
xについて解け
$\frac{1}{x} - \frac{2}{xy} = 3y$
智弁学園和歌山高等学校
ただの計算

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを計算せよ.
$\left(\dfrac{4}{(\sqrt5+1)(\sqrt[4]{5}+1)(\sqrt[8]{5}+1)(\sqrt[16]{5}+1)}+1\right)^{48}$
この動画を見る
これを計算せよ.
$\left(\dfrac{4}{(\sqrt5+1)(\sqrt[4]{5}+1)(\sqrt[8]{5}+1)(\sqrt[16]{5}+1)}+1\right)^{48}$
福田のわかった数学〜高校2年生049〜領域(4)命題と領域

単元:
#数Ⅰ#数Ⅱ#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 領域(4) 領域と命題
次の条件$(\textrm{A}),\ (\textrm{B})$は同値であることを示せ。
$(\textrm{A})\ |x+y| \leqq 1$かつ$|x-y| \leqq 1$
$(\textrm{B})\ |x|+|y| \leqq 1$
この動画を見る
数学$\textrm{II}$ 領域(4) 領域と命題
次の条件$(\textrm{A}),\ (\textrm{B})$は同値であることを示せ。
$(\textrm{A})\ |x+y| \leqq 1$かつ$|x-y| \leqq 1$
$(\textrm{B})\ |x|+|y| \leqq 1$
【数学Ⅰ】命題と集合 基本をザザッと

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
15の正の約数全体の集合をAとする。
(1)3____A
(2)5____A
(3)7____A
(4)1____A
(5)15____A
(6)6____A
(7)8____A
-----------------
(1)8以下の自然数全体の集合
(2){$x|-3 \leqq x \leqq 1,x$は整数}
この動画を見る
15の正の約数全体の集合をAとする。
(1)3____A
(2)5____A
(3)7____A
(4)1____A
(5)15____A
(6)6____A
(7)8____A
-----------------
(1)8以下の自然数全体の集合
(2){$x|-3 \leqq x \leqq 1,x$は整数}
どっちが難しい?智弁対決 智弁学園VS智弁和歌山

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xの不等式において定数aの値の範囲は?
・$4x \leqq 5-3a$の解が自然数を1つも含まないとき 2001智辯学園高等学校
・x<aを満たす自然数xがちょうど3コのとき 2002智辯学園和歌山高等学校
この動画を見る
xの不等式において定数aの値の範囲は?
・$4x \leqq 5-3a$の解が自然数を1つも含まないとき 2001智辯学園高等学校
・x<aを満たす自然数xがちょうど3コのとき 2002智辯学園和歌山高等学校
簡単な計算問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt{\dfrac{2021^3-2019^3-2}{6}}$
この動画を見る
これを解け.
$\sqrt{\dfrac{2021^3-2019^3-2}{6}}$
福田のわかった数学〜高校2年生046〜領域(1)連立不等式の表す領域

単元:
#数Ⅰ#数Ⅱ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy\lt 1 \\
xy(x^2-y^2)(x^2+y^2-2)\gt 0
\end{array}
\right.
\end{eqnarray}$
の表す領域を図示せよ.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy\lt 1 \\
xy(x^2-y^2)(x^2+y^2-2)\gt 0
\end{array}
\right.
\end{eqnarray}$
の表す領域を図示せよ.
