 数と式
数と式
 数と式
数と式
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.2 0!はいくつ?

単元:
#数Ⅰ#数A#数と式#場合の数と確率#式の計算(整式・展開・因数分解)#場合の数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.2 0!はいくつ?
この動画を見る
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.2 0!はいくつ?
【テスト対策・中3】1章-3

単元:
#数学(中学生)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$a+b=7,ab=3$のとき,$a^2+b^2$の値を求めなさい.
②5600にできるだけ小さい自然数$n$をかけて,
その積がある自然数の2乗になるようにしたい.
このときの$n$の値を求めなさい.
③$\dfrac{455}{n+2}$が自然数となるような素数$n$を
すべて求めなさい.
この動画を見る
①$a+b=7,ab=3$のとき,$a^2+b^2$の値を求めなさい.
②5600にできるだけ小さい自然数$n$をかけて,
その積がある自然数の2乗になるようにしたい.
このときの$n$の値を求めなさい.
③$\dfrac{455}{n+2}$が自然数となるような素数$n$を
すべて求めなさい.
【テスト対策・中1】1章-2

単元:
#数学(中学生)#中1数学#正の数・負の数#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①絶対値が7である整数をすべて書きなさい.
②絶対値が4.1より小さい整数の個数を書きなさい.
③絶対値が3より大きく5以下になる整数をすべて書きなさい.
④絶対値が2以上7未満になる整数の個数を書きなさい.
この動画を見る
①絶対値が7である整数をすべて書きなさい.
②絶対値が4.1より小さい整数の個数を書きなさい.
③絶対値が3より大きく5以下になる整数をすべて書きなさい.
④絶対値が2以上7未満になる整数の個数を書きなさい.
【高校数学】数Ⅲ-12 ド・モアブルの定理①

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の値を計算しよう.
②$\left(\dfrac{\sqrt3}{2}+\dfrac{1}{2}i\right)^{12}$
③$(1+i)^6$
この動画を見る
次の値を計算しよう.
②$\left(\dfrac{\sqrt3}{2}+\dfrac{1}{2}i\right)^{12}$
③$(1+i)^6$
【高校受験対策】数学-死守26

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#数と式#確率#円#一次不等式(不等式・絶対値のある方程式・不等式)#文章題#文章題その他
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$-3+8$を計算しなさい.
②$2(2x - y) - (x - y)$を計算しなさい.
③$\sqrt{27}-\sqrt{63}$を計算しなさい.
④$(x + 5)(x - 3)$を展開しなさい.
⑤$a(b + 8) - (b + 8)$を因数分解しなさい.
⑥2次方程式 $x ^ 2 + x = 3$を解きなさい.
⑦右の図1の円$O$において,
$\angle x$と$\angle y$の大きさをそれぞれ求めなさい.
⑧鉛筆1本の値段を$a$円,ノート1冊の値段を$b$円とする.
「鉛筆3本とノート1冊の代金を払うと,
300円でおつりがもらえた」という数量の関係を,
不等式で表しなさい.ただし,値段は税込みとする.
⑨箱の中に,25本の当たりを含むたくさんのくじが入っている.
このくじをよくかき混ぜた後,48人がこの箱から1人1回ずつくじを引いたところ,
当たりが2本出た.箱の中に最初に入っていたくじの本数は,
およそ何本であったと推定できるか,求めなさい.
⑩ある水族館の入館料は,おとな3人と子ども2人で入ると4020円かかり,
おとな1人と子ども3人で入ると2600円かかる.
おとな1人,子ども1人の入館料をそれぞれ求めなさい.
ただし,入館料は税込みとする.
図は動画内参照
この動画を見る
①$-3+8$を計算しなさい.
②$2(2x - y) - (x - y)$を計算しなさい.
③$\sqrt{27}-\sqrt{63}$を計算しなさい.
④$(x + 5)(x - 3)$を展開しなさい.
⑤$a(b + 8) - (b + 8)$を因数分解しなさい.
⑥2次方程式 $x ^ 2 + x = 3$を解きなさい.
⑦右の図1の円$O$において,
$\angle x$と$\angle y$の大きさをそれぞれ求めなさい.
⑧鉛筆1本の値段を$a$円,ノート1冊の値段を$b$円とする.
「鉛筆3本とノート1冊の代金を払うと,
300円でおつりがもらえた」という数量の関係を,
不等式で表しなさい.ただし,値段は税込みとする.
⑨箱の中に,25本の当たりを含むたくさんのくじが入っている.
このくじをよくかき混ぜた後,48人がこの箱から1人1回ずつくじを引いたところ,
当たりが2本出た.箱の中に最初に入っていたくじの本数は,
およそ何本であったと推定できるか,求めなさい.
⑩ある水族館の入館料は,おとな3人と子ども2人で入ると4020円かかり,
おとな1人と子ども3人で入ると2600円かかる.
おとな1人,子ども1人の入館料をそれぞれ求めなさい.
ただし,入館料は税込みとする.
図は動画内参照
【高校受験対策】数学-死守20

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#数と式#比例・反比例#確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$(-2)+11$を計算しなさい.
②$(- 4) ^ 2 \times (- 3)$を計算しなさい.
③$(6a - 15b) \div 3$を計算しなさい.
④$(2x - 1)(x + 3)$を展開しなさい.
⑤$x ^ 2 - (y + 3) ^ 2$ を因数分解しなさい.
⑥方程式$\dfrac{x - 2}{4} + \dfrac{2 - 5x}{6} = 1$を解きなさい.
⑦$y$は$x$に反比例し,$x = 2$ のとき $y = - 3$ である.
このとき,$y$を$x$の式で表しなさい.
⑧次のア~オの中から,無理数をすべて選び,記号で答えなさい.
ア.$\dfrac{1}{3}$
イ.$\sqrt5$
ウ.$0.25$
エ.$-2\sqrt3$
オ.$\sqrt6$
⑨右の図のア~エは,関数$y = ax ^ 2$のグラフである.
次の(1),(2)の問いに答えなさい.
(1)関数$y=\dfrac{1}{2}x^2$のグラフを,ア~エから選びなさい.
(2)$x$の値が$-2$から$-1$まで増加するときの
変化の割合が最も大きい関数のグラフを,ア~エから選びなさい.
また,そのときの変化の割合を求めなさい.
⑩袋の中に$0,1,2,3$の数字が1つずつ書かれた4個の玉が入っている.
この袋から玉を1個取り出して玉に書かれた数字を確認して,
それを袋の中にもどしてから,また1個取り出すとき,
(1)取り出した2個の玉に書かれていた数字が同じになる確率を求めなさい.
(2)次の$\Box$に適することばを入れて,
求める確率が$\dfrac{1}{4}$となる問題を1つ完成させなさい.
「取り出した2個の玉の数字の積が$\Box$になる確率を求めなさい.」
図は動画内参照
この動画を見る
①$(-2)+11$を計算しなさい.
②$(- 4) ^ 2 \times (- 3)$を計算しなさい.
③$(6a - 15b) \div 3$を計算しなさい.
④$(2x - 1)(x + 3)$を展開しなさい.
⑤$x ^ 2 - (y + 3) ^ 2$ を因数分解しなさい.
⑥方程式$\dfrac{x - 2}{4} + \dfrac{2 - 5x}{6} = 1$を解きなさい.
⑦$y$は$x$に反比例し,$x = 2$ のとき $y = - 3$ である.
このとき,$y$を$x$の式で表しなさい.
⑧次のア~オの中から,無理数をすべて選び,記号で答えなさい.
ア.$\dfrac{1}{3}$
イ.$\sqrt5$
ウ.$0.25$
エ.$-2\sqrt3$
オ.$\sqrt6$
⑨右の図のア~エは,関数$y = ax ^ 2$のグラフである.
次の(1),(2)の問いに答えなさい.
(1)関数$y=\dfrac{1}{2}x^2$のグラフを,ア~エから選びなさい.
(2)$x$の値が$-2$から$-1$まで増加するときの
変化の割合が最も大きい関数のグラフを,ア~エから選びなさい.
また,そのときの変化の割合を求めなさい.
⑩袋の中に$0,1,2,3$の数字が1つずつ書かれた4個の玉が入っている.
この袋から玉を1個取り出して玉に書かれた数字を確認して,
それを袋の中にもどしてから,また1個取り出すとき,
(1)取り出した2個の玉に書かれていた数字が同じになる確率を求めなさい.
(2)次の$\Box$に適することばを入れて,
求める確率が$\dfrac{1}{4}$となる問題を1つ完成させなさい.
「取り出した2個の玉の数字の積が$\Box$になる確率を求めなさい.」
図は動画内参照
【高校数学】 数A-81 有限小数と循環小数

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
既約分数の形にしたとき,分母の素因数が
①と①のみの分数は有限小数となる.
②右の分数のうち,有限小数となるものを選ぼう.
$\dfrac{12}{55},\dfrac{6}{105},\dfrac{9}{240},\dfrac{126}{450}$
③分数$\dfrac{11}{101}$を小数で表したとき,
小数第$75$の数字を求めよう.
この動画を見る
既約分数の形にしたとき,分母の素因数が
①と①のみの分数は有限小数となる.
②右の分数のうち,有限小数となるものを選ぼう.
$\dfrac{12}{55},\dfrac{6}{105},\dfrac{9}{240},\dfrac{126}{450}$
③分数$\dfrac{11}{101}$を小数で表したとき,
小数第$75$の数字を求めよう.
【高校数学】「論理と集合」と「ベン図」をたぶん日本一わかりやすく解説した動画【篠原好】

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
「論理と集合」について、わかりやすく解説しています。
この動画を見る
「論理と集合」について、わかりやすく解説しています。
【高校数学】 数Ⅰ-75 絶対値を含む関数のグラフ②

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$y=| 2x^2-4x-6 |$のグラフを書こう。
この動画を見る
◎$y=| 2x^2-4x-6 |$のグラフを書こう。
【高校数学】 数Ⅰ-74 絶対値を含む関数のグラフ①
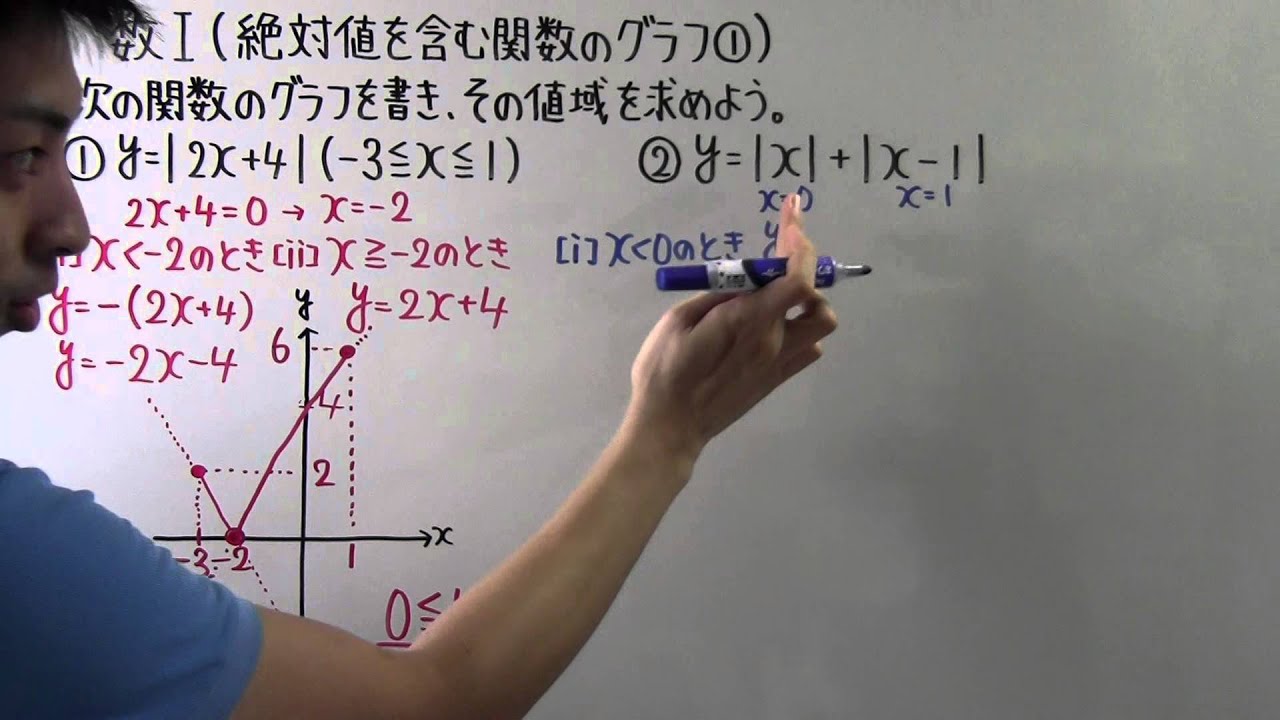
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の関数のグラフを書き、その値域を求めよう。
①$y=| 2x+4 |(-3 \leqq x \leqq 1)$
②$y=| x |+| x-1 |$
この動画を見る
◎次の関数のグラフを書き、その値域を求めよう。
①$y=| 2x+4 |(-3 \leqq x \leqq 1)$
②$y=| x |+| x-1 |$
【高校数学】数Ⅰ-34 命題⑧
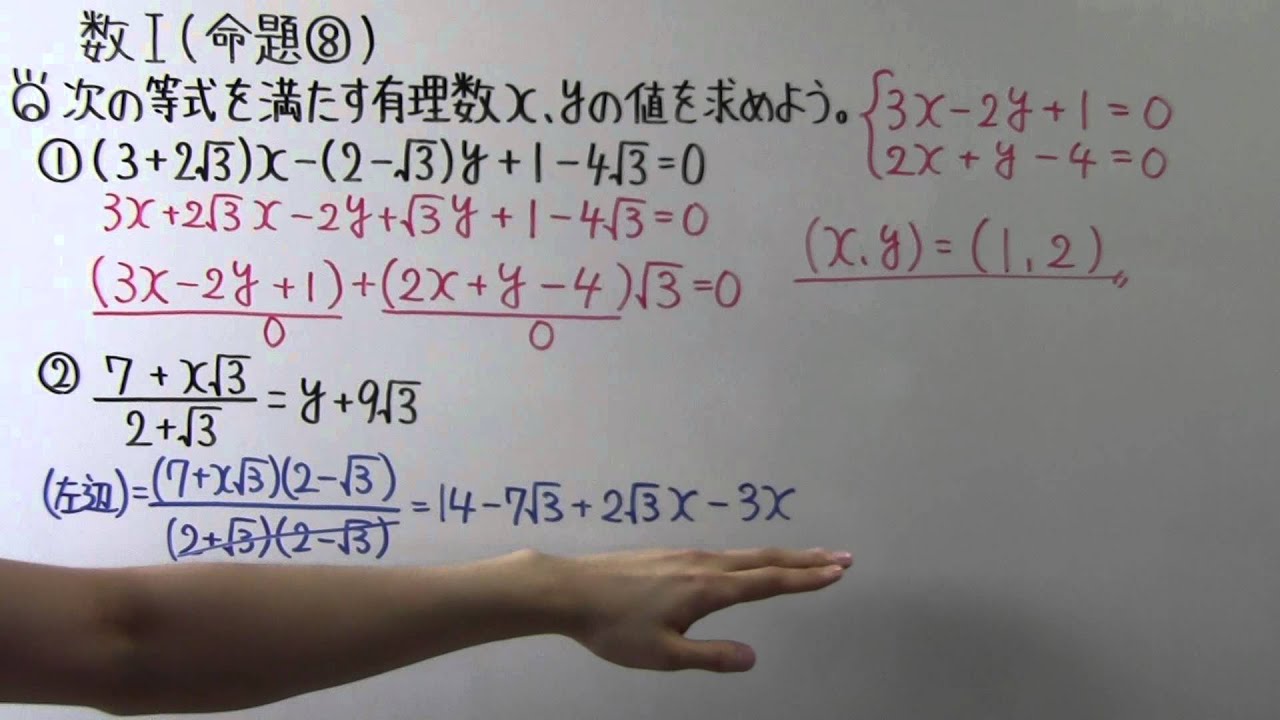
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の等式を満たす有理数x,yの値を求めよう。
①$(3+2\sqrt{ 3 })x-(2-\sqrt{ 3 })y+1-4\sqrt{ 3 }=0$
②$\displaystyle \frac{7+x\sqrt{ 3 }}{2+\sqrt{ 3 }}=y+9\sqrt{ 3 }$
この動画を見る
◎次の等式を満たす有理数x,yの値を求めよう。
①$(3+2\sqrt{ 3 })x-(2-\sqrt{ 3 })y+1-4\sqrt{ 3 }=0$
②$\displaystyle \frac{7+x\sqrt{ 3 }}{2+\sqrt{ 3 }}=y+9\sqrt{ 3 }$
【高校数学】数Ⅰ-33 命題⑦(続 背理法編)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎命題「nは整数とする。$n^2$が3倍ならば、nは3倍数である」は真である。
これを利用して、$\sqrt{ 3 }$が無理であることを証明しよう。
この動画を見る
◎命題「nは整数とする。$n^2$が3倍ならば、nは3倍数である」は真である。
これを利用して、$\sqrt{ 3 }$が無理であることを証明しよう。
【高校数学】数Ⅰ-32 命題⑥(背理法編)

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$\sqrt{ 2 }$が無理数であることを用いて、$5-\sqrt{ 2 }$が無理数であることを証明しよう。
この動画を見る
◎$\sqrt{ 2 }$が無理数であることを用いて、$5-\sqrt{ 2 }$が無理数であることを証明しよう。
【高校数学】数Ⅰ-31 命題⑤

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数とする。
次の命題の逆、裏、対偶を書き、それぞれ真偽を調べよう。
①$x=-1$ならば$x^2=1$
[逆]
[裏]
[対偶]
②$x+y>2$ならば$x>0$または$y>2$
[逆]
[裏]
[対偶]
この動画を見る
◎x,yは実数とする。
次の命題の逆、裏、対偶を書き、それぞれ真偽を調べよう。
①$x=-1$ならば$x^2=1$
[逆]
[裏]
[対偶]
②$x+y>2$ならば$x>0$または$y>2$
[逆]
[裏]
[対偶]
【高校数学】数Ⅰ-30 命題④

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数、m,nは自然数とする。
次の条件の否定を書こう。
①$x<-1$かつ$y \geqq 2$
②$-5 \leqq x<3$
③nは奇数または3の倍数
④m,nともに6の倍数
◎次の命題の否定を書き、その真偽を調べよう。
⑤すべての素数nについて、nは奇数である。
この動画を見る
◎x,yは実数、m,nは自然数とする。
次の条件の否定を書こう。
①$x<-1$かつ$y \geqq 2$
②$-5 \leqq x<3$
③nは奇数または3の倍数
④m,nともに6の倍数
◎次の命題の否定を書き、その真偽を調べよう。
⑤すべての素数nについて、nは奇数である。
【高校数学】数Ⅰ-29 命題③

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$xy=0$は、$x^2+y^2>0$が成立するための▭
②$△ABC∞△PQR$は、$△ABC \equiv △PQR$であるための▭
③$|x|<1$かつ$|y|<1$は、$x^2+y^2<1$であるための▭
この動画を見る
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$xy=0$は、$x^2+y^2>0$が成立するための▭
②$△ABC∞△PQR$は、$△ABC \equiv △PQR$であるための▭
③$|x|<1$かつ$|y|<1$は、$x^2+y^2<1$であるための▭
【高校数学】数Ⅰ-28 命題②

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$x=2$は、$x^2-x-2=0$であるための▭
②$xy=0$は、$x=0$であるための▭
③$|x|=0$は、$x=0$であるための▭
④$xy>1$は、$x>1$であるための▭
この動画を見る
◎x,yは実数とする。
次の▭にあてはまるものを、下のⒶ~Ⓓから選ぼう。
Ⓐ必要十分条件である
Ⓑ必要条件ではあるが、十分条件ではない
Ⓒ十分条件ではあるが、必要条件ではない
Ⓓ必要条件でも十分条件でもない
①$x=2$は、$x^2-x-2=0$であるための▭
②$xy=0$は、$x=0$であるための▭
③$|x|=0$は、$x=0$であるための▭
④$xy>1$は、$x>1$であるための▭
【高校数学】数Ⅰ-27 命題①

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎a,b,cは実数、dは自然数とする。
次の命題の真偽を調べ、偽のときは判例を1つ示そう。
①$a=0$ならば$ab=0$
②$a^2=b^2$ならば$a=b$
③$a<2$ならば$|a|<4$
④dは2倍の倍数 ならば dの4の倍数
⑤$|a|<3$ならば$a<3$
⑥dは18の約数ならばdは36の約数
この動画を見る
◎a,b,cは実数、dは自然数とする。
次の命題の真偽を調べ、偽のときは判例を1つ示そう。
①$a=0$ならば$ab=0$
②$a^2=b^2$ならば$a=b$
③$a<2$ならば$|a|<4$
④dは2倍の倍数 ならば dの4の倍数
⑤$|a|<3$ならば$a<3$
⑥dは18の約数ならばdは36の約数
【高校数学】数Ⅰ-26 集合③
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
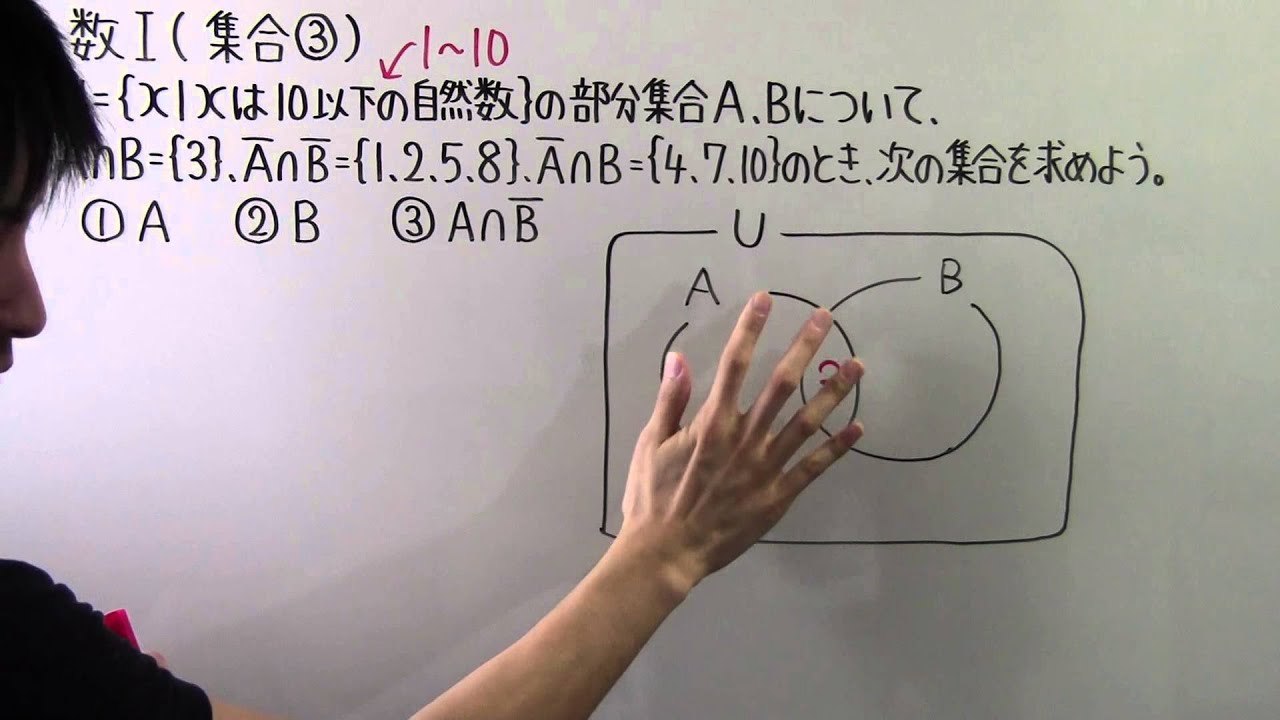
◎U={$x | x$は10以下の自然数}を全体集合とする。
$A \cap B={3}、\overline{ A } \cap \overline{ B }={1,2,5,8,}、\overline{ A } \cap B={4,7,10}$
のとき、次の集合を求めよう。
①$A$
②$B$
③$A \cap\overline{ B}$
この動画を見る
◎U={$x | x$は10以下の自然数}を全体集合とする。
$A \cap B={3}、\overline{ A } \cap \overline{ B }={1,2,5,8,}、\overline{ A } \cap B={4,7,10}$
のとき、次の集合を求めよう。
①$A$
②$B$
③$A \cap\overline{ B}$
【高校数学】数Ⅰ-25 集合②

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎U={$x | x$は9以下の自然数}を全体集合とする。
$U$の部分集合$A={1.3.4.8},B={3.4.5.7.9}$,$C={2,3,7,9}$について、次の集合を求めよう。
①$A \cap B \cap C$
②$A \cap B \cap \overline{ C }$
③$\overline{ A } \cap B \cap C$
④$ \overline{ A \cup B \cup C} $
⑤$\overline{ A } \cap B \cap C$
⑥$(A \cup C) \cap \overline{ B} $
この動画を見る
◎U={$x | x$は9以下の自然数}を全体集合とする。
$U$の部分集合$A={1.3.4.8},B={3.4.5.7.9}$,$C={2,3,7,9}$について、次の集合を求めよう。
①$A \cap B \cap C$
②$A \cap B \cap \overline{ C }$
③$\overline{ A } \cap B \cap C$
④$ \overline{ A \cup B \cup C} $
⑤$\overline{ A } \cap B \cap C$
⑥$(A \cup C) \cap \overline{ B} $
【高校数学】数Ⅰ-24 集合①

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$U={1.2.3.4.5.6.7.8.9.10}$を全体集合とする。
$U$の部分集合$A={1.2.3.4.8},B={1.3.5.7.9}$について、次の集合を求めよう。
①$A \cap B$
②$A \cup B$
③$\overline{ A } \cap \overline{ B }$
④$ A \cup \overline{ B }$
⑤$\overline{ A } \cap B $
⑥$\overline{ A \cup B} $
この動画を見る
◎$U={1.2.3.4.5.6.7.8.9.10}$を全体集合とする。
$U$の部分集合$A={1.2.3.4.8},B={1.3.5.7.9}$について、次の集合を求めよう。
①$A \cap B$
②$A \cup B$
③$\overline{ A } \cap \overline{ B }$
④$ A \cup \overline{ B }$
⑤$\overline{ A } \cap B $
⑥$\overline{ A \cup B} $
【高校数学】数Ⅰ-23 絶対値を含む方程式・不等式③(続 応用編)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\sqrt{ x^2 }+\sqrt{ x^2-4x+4 }=4$
②$|x|-2|x+3|\geqq 0$
この動画を見る
①$\sqrt{ x^2 }+\sqrt{ x^2-4x+4 }=4$
②$|x|-2|x+3|\geqq 0$
【高校数学】数Ⅰ-22 絶対値を含む方程式・不等式②(応用編)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$|x-3|=4x$
②$|x-4| \leqq 3x$
③$|x+2|\gt 3x$
この動画を見る
①$|x-3|=4x$
②$|x-4| \leqq 3x$
③$|x+2|\gt 3x$
【高校数学】数Ⅰ-21 絶対値を含む方程式・不等式①(基本編)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$a \gt 0$のとき、$|x|=a$の解は①____、$|x|\lt a$の解は②____、$|x| \gt a$の解は③____となる。
④$|x+2|=5$
⑤$|x+3|\lt 7$
⑥$|x+4|\gt 3$
⑦$|3x-1|\geqq 5$
⑧$|5x-3| \leqq 2$
⑨$|6-x| \gt 4$
この動画を見る
$a \gt 0$のとき、$|x|=a$の解は①____、$|x|\lt a$の解は②____、$|x| \gt a$の解は③____となる。
④$|x+2|=5$
⑤$|x+3|\lt 7$
⑥$|x+4|\gt 3$
⑦$|3x-1|\geqq 5$
⑧$|5x-3| \leqq 2$
⑨$|6-x| \gt 4$
【高校数学】数Ⅰ-19 1次不等式③(連立不等式編)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 8 \geqq 4x+2 \\
3x + 4 \gt -2x
\end{array}
\right.
\end{eqnarray}$
②$\begin{eqnarray}
\left\{
\begin{array}{l}
5x \lt 2(x-6) \\
7 - 2x \geqq 3x-8x
\end{array}
\right.
\end{eqnarray}$
③$2x-1\lt5x+8\lt7x+4$
この動画を見る
①$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 8 \geqq 4x+2 \\
3x + 4 \gt -2x
\end{array}
\right.
\end{eqnarray}$
②$\begin{eqnarray}
\left\{
\begin{array}{l}
5x \lt 2(x-6) \\
7 - 2x \geqq 3x-8x
\end{array}
\right.
\end{eqnarray}$
③$2x-1\lt5x+8\lt7x+4$
【高校数学】数Ⅰ-20 1次不等式④(応用編)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①不等式$3x-a \lt 2(5-x)$を満たすxのうちで最大整数が5であるとき、定数aの値の範囲は?
②とある店では500円で会員になることができ、会員は10%引きで買い物ができる。
この店で定価600円の品物を買うとき、会員になった方が合計金額が安くなるのは何個以上買うとき?
この動画を見る
①不等式$3x-a \lt 2(5-x)$を満たすxのうちで最大整数が5であるとき、定数aの値の範囲は?
②とある店では500円で会員になることができ、会員は10%引きで買い物ができる。
この店で定価600円の品物を買うとき、会員になった方が合計金額が安くなるのは何個以上買うとき?
【高校数学】数Ⅰ-18 1次不等式②(練習編)
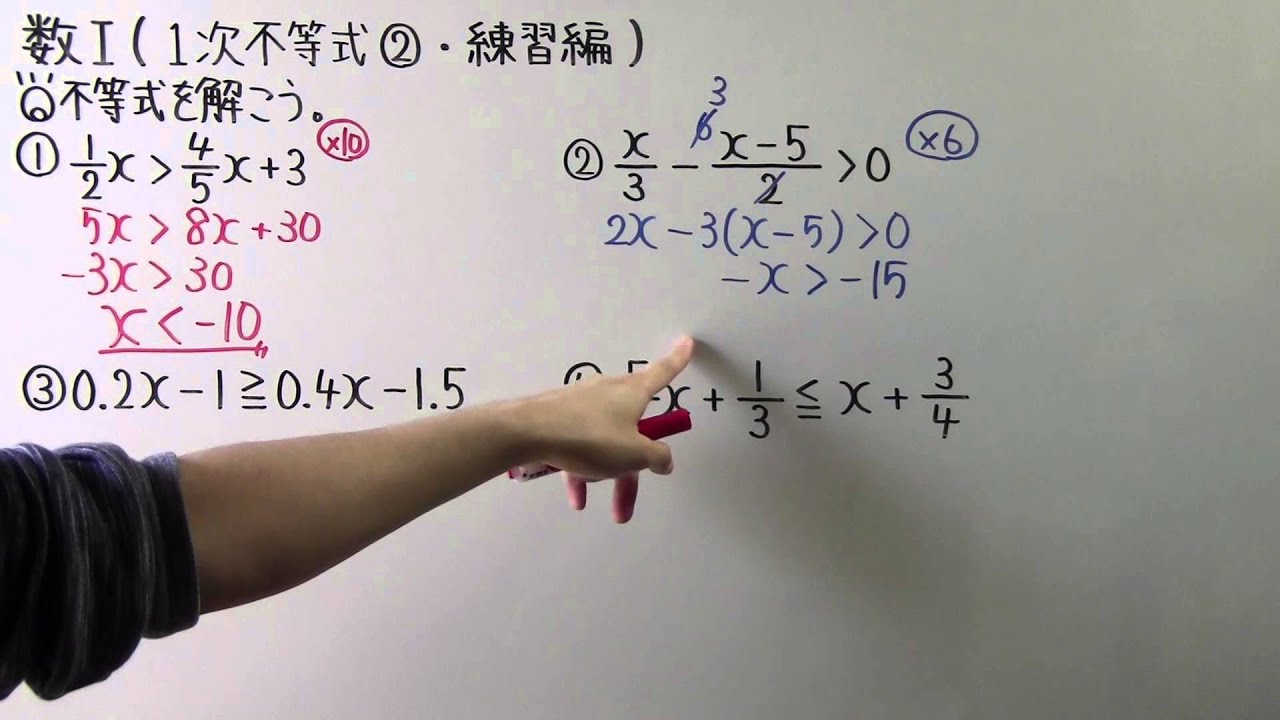
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎不等式を解こう。
①$\displaystyle \frac{1}{2}x \gt \displaystyle \frac{4}{5}x+3$
②$\displaystyle \frac{x}{3}-\displaystyle \frac{x-5}{2} \gt 0$
③$0.2x-1 \geqq 0.4x -1.5$
④$\displaystyle \frac{5}{6}x+\displaystyle \frac{1}{3} \leqq x+\displaystyle \frac{3}{4}$
この動画を見る
◎不等式を解こう。
①$\displaystyle \frac{1}{2}x \gt \displaystyle \frac{4}{5}x+3$
②$\displaystyle \frac{x}{3}-\displaystyle \frac{x-5}{2} \gt 0$
③$0.2x-1 \geqq 0.4x -1.5$
④$\displaystyle \frac{5}{6}x+\displaystyle \frac{1}{3} \leqq x+\displaystyle \frac{3}{4}$
【高校数学】数Ⅰ-17 1次不等式①(基本編)
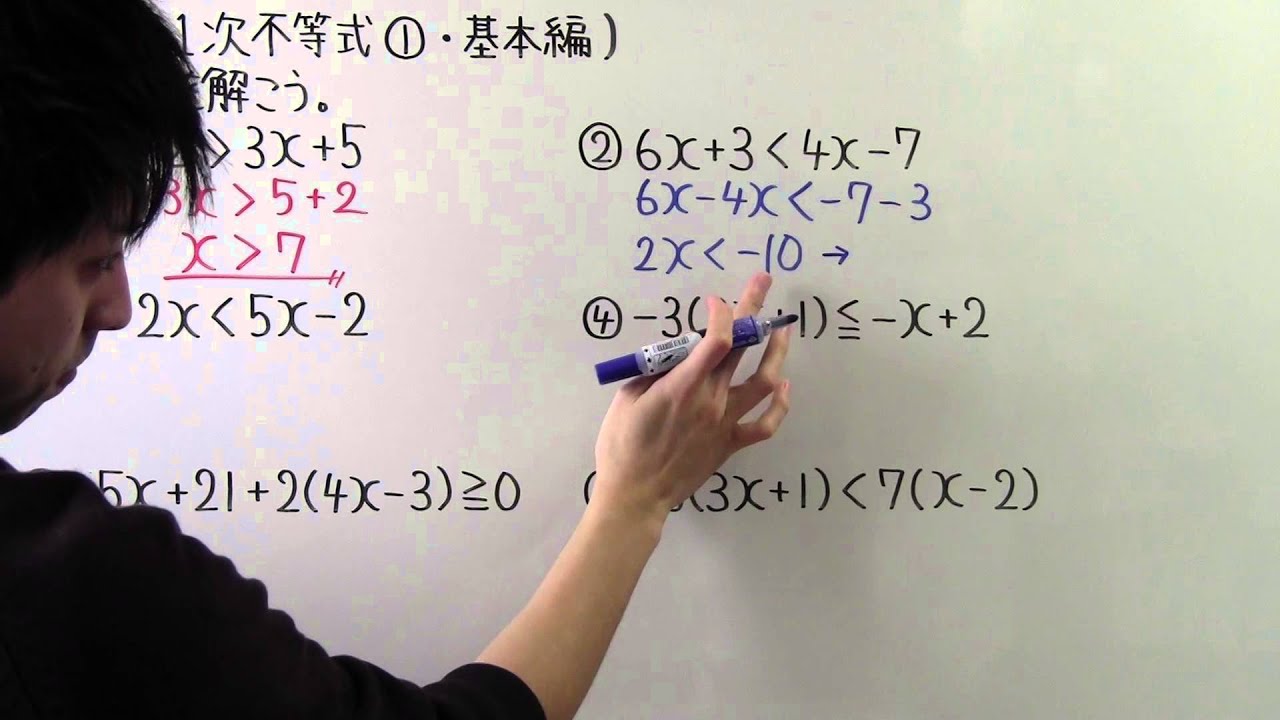
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎不等式を解こう。
①$4x-2\gt3x+5$
②$6x+3\lt4x-7$
③$7+2x\lt5x-2$
④$-3(2x+1)\leqq-x+2$
⑤$-5x+21+2(4x-3)\geqq0$
⑥$-3(3x+1)\lt7(x-2)$
この動画を見る
◎不等式を解こう。
①$4x-2\gt3x+5$
②$6x+3\lt4x-7$
③$7+2x\lt5x-2$
④$-3(2x+1)\leqq-x+2$
⑤$-5x+21+2(4x-3)\geqq0$
⑥$-3(3x+1)\lt7(x-2)$
【高校数学】数Ⅰ-16 √(ルート)シリーズ④(二重根号編)
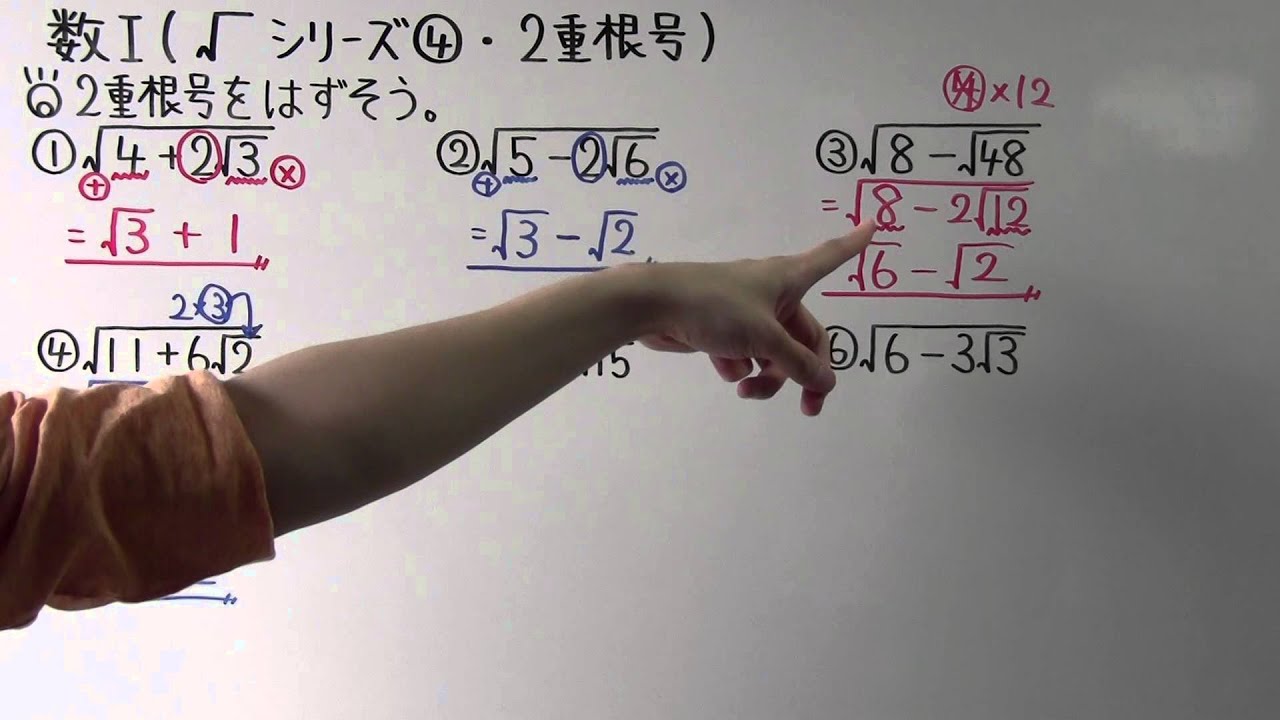
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎2重根号を外そう。
①$\sqrt{ 4+2\sqrt{ 3 } }$
②$\sqrt{ 5-2\sqrt{ 6 } }$
③$\sqrt{ 8-\sqrt{ 48 } }$
④$\sqrt{ 11+6\sqrt{ 2 } }$
⑤$\sqrt{ 4+\sqrt{ 15 } }$
⑥$\sqrt{ 6-3\sqrt{ 3 } }$
この動画を見る
◎2重根号を外そう。
①$\sqrt{ 4+2\sqrt{ 3 } }$
②$\sqrt{ 5-2\sqrt{ 6 } }$
③$\sqrt{ 8-\sqrt{ 48 } }$
④$\sqrt{ 11+6\sqrt{ 2 } }$
⑤$\sqrt{ 4+\sqrt{ 15 } }$
⑥$\sqrt{ 6-3\sqrt{ 3 } }$
【高校数学】数Ⅰ-15 √(ルート)シリーズ③(応用編)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎$\displaystyle \frac{1}{2-\sqrt{ 3 }}$の整数部分を$a$、小数部分を$b$とする。
①$a,b$の値は?
②$a+4b+2b^2+2$の値は?
②次の各場合について、$\sqrt{ x^2+6+9 }$を$x$の整式で表そう。
③$x \geqq -3$
④$x \lt -3$
この動画を見る
◎$\displaystyle \frac{1}{2-\sqrt{ 3 }}$の整数部分を$a$、小数部分を$b$とする。
①$a,b$の値は?
②$a+4b+2b^2+2$の値は?
②次の各場合について、$\sqrt{ x^2+6+9 }$を$x$の整式で表そう。
③$x \geqq -3$
④$x \lt -3$
