２次関数
２次関数
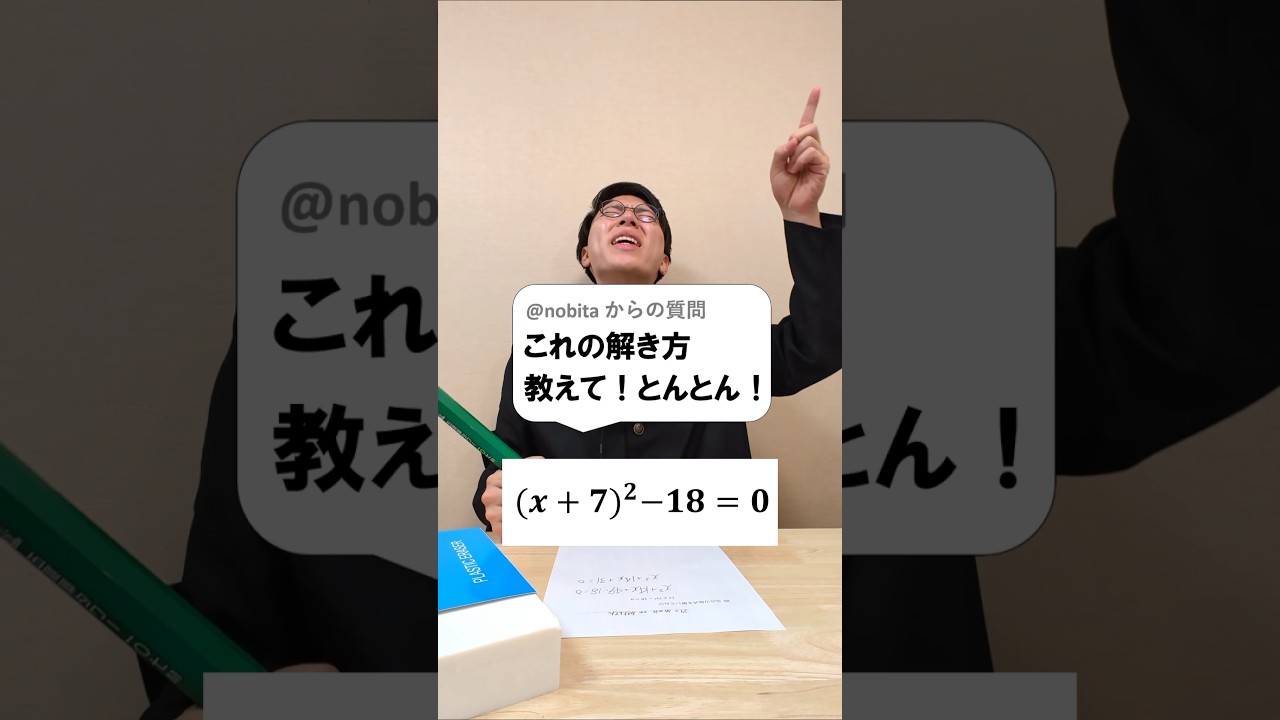
【数Ⅰ】【2次関数】不等式 x²+9x+18＜0 を満たすすべてのxが不等式 x²-4ax+3a＜0 を満たすような定数a の値の範囲を求めよ。
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
不等式 x²+9x+18＜0 を満たすすべてのxが不等式 x²-4ax+3a＜0 を満たすような定数a の値の範囲を求めよ。
この動画を見る
不等式 x²+9x+18＜0 を満たすすべてのxが不等式 x²-4ax+3a＜0 を満たすような定数a の値の範囲を求めよ。
【数Ⅰ】【2次関数】aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
この動画を見る
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
【数Ⅰ】【2次関数】(1) y=|x²+2x|のグラフを描け。(2) |x²+2x|=k の実数解の個数を求めよ。
【数Ⅰ】【2次関数】グラフを利用して、次の不等式を解け。(1) |x+1|＜2x (2) |x²-4| ＞-3x
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
グラフを利用して、次の不等式を解け。
(1) |x+1|＜2x
(2) |x²-4| ＞-3x
この動画を見る
グラフを利用して、次の不等式を解け。
(1) |x+1|＜2x
(2) |x²-4| ＞-3x
【数Ⅰ】【2次関数】x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
この動画を見る
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
【数Ⅰ】【2次関数】x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
この動画を見る
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
【数Ⅰ】【2次関数】次の条件を満たすような定数a の値の範囲を求めよ。(1) 二次方程式 2x²-3x+a=0 の1つの解が 0＜x＜1 の範囲にあり、他の解が 0＜x＜1 の範囲にある。他1問
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0＜x＜1 の範囲にあり、他の解が 0＜x＜1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1＜x＜0 の範囲にあり、他の解が 2＜x＜3 の範囲にある。ただし a＞0 とする。
この動画を見る
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0＜x＜1 の範囲にあり、他の解が 0＜x＜1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1＜x＜0 の範囲にあり、他の解が 2＜x＜3 の範囲にある。ただし a＞0 とする。
【数Ⅰ】【2次関数】a＜b＜c のとき(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0の2つの解のうち１つは a＜x＜b の範囲にありもう1つは b＜x＜c の範囲にあることを示せ
【数Ⅰ】【2次関数】放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
この動画を見る
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
【数Ⅰ】【2次関数】放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
この動画を見る
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
【数Ⅰ】【2次関数】次の関数に最大値・最小値があればそれを求めよ。(1) y=-2x⁴+4x²+3(2) y=(x²-2x)²+4(x²-2x)-1
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
この動画を見る
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
福田の数学〜早稲田大学2025人間科学部第2問〜絶対値の付いた関数の最小
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学516〜2次方程式が自然数解を持つ条件
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2-2ax+b=0$
$x^2-2bx+c=0$
$x^2-2cx+a=0$
がすべて自然数解をもつ。
このような自然数の組$(a,b,c)$を
すべて求めて下さい。
この動画を見る
$x^2-2ax+b=0$
$x^2-2bx+c=0$
$x^2-2cx+a=0$
がすべて自然数解をもつ。
このような自然数の組$(a,b,c)$を
すべて求めて下さい。
2次関数（放物線）折ることできる？
何を折っているでしょう？
福田の数学〜慶應義塾大学薬学部2025第1問(1)〜絶対不等式と2次関数の最大最小
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(1)$a$を実数とする。
$x$の$2$次関数$f(x)＝x^2-ax+a+2$は、
すべての実数$x$に対して$f(x)\geqq 0$を満たす。
(i)$a$の値の範囲は$\boxed{ア}$である。
(ii)$-2\leqq x\leqq 3$において、$f(x)$の最大値を$m$,
最大値を$M$とおく。
$m$が最大となるのは$a=\boxed{イ}$のときであり、
このとき$m=\boxed{ウ},M=\boxed{エ}$である。
$2025$年慶應義塾大学薬学部過去問題
【中学数学】2次関数の問題～2024年度北海道公立高校入試大問3～【高校受験】
単元：
#数学(中学生)#中３数学#数Ⅰ#２次関数#2次関数#2次関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
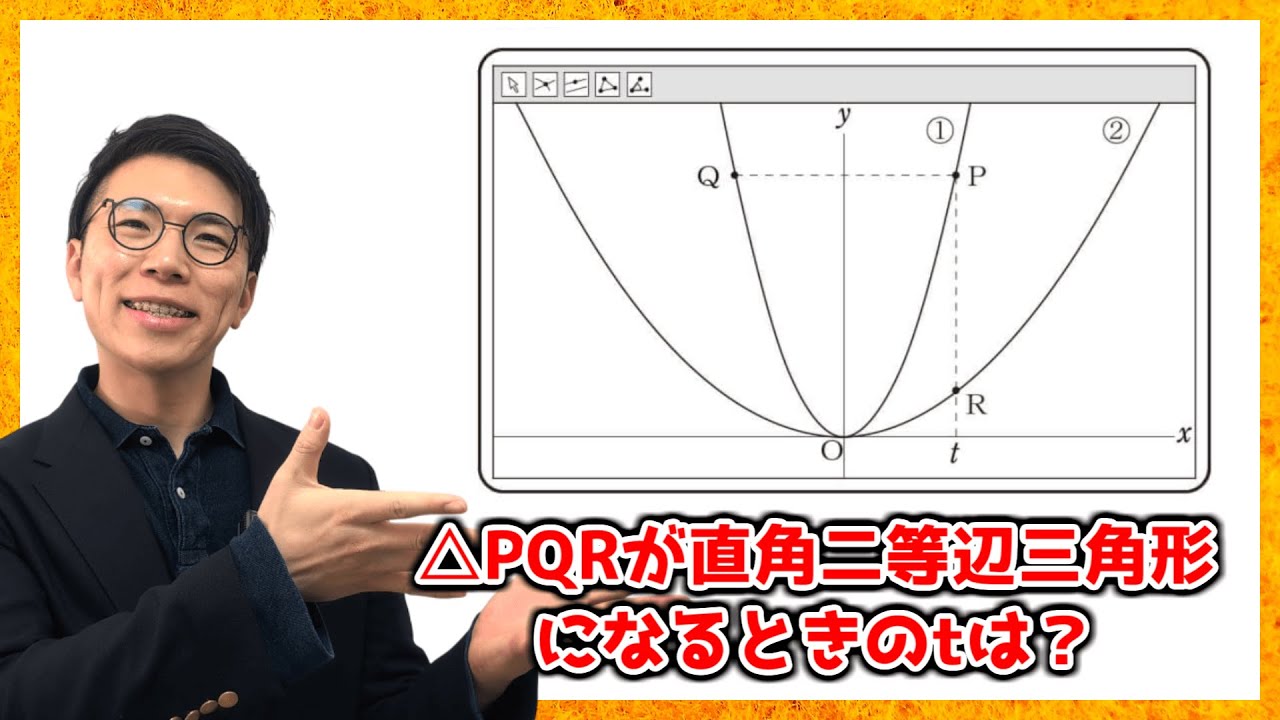
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①，$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$＞0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ？△PQRが直角に等辺三角形に見えるときがあるよ？」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
この動画を見る
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①，$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$＞0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ？△PQRが直角に等辺三角形に見えるときがあるよ？」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
２つの二次方程式 2025立教新座
単元：
#２次関数#2次方程式と2次不等式
指導講師：
数学を数楽に
問題文全文(内容文)：
2つの2次方程式 \begin{eqnarray}
x^2 -kx-10 = 0
\end{eqnarray}
\begin{eqnarray}
x^2+5x+2k=0
\end{eqnarray}
が共通解を1つだけ持つ。この共通解と定数kを求めよ。ただしk≠-5
この動画を見る
2つの2次方程式 \begin{eqnarray}
x^2 -kx-10 = 0
\end{eqnarray}
\begin{eqnarray}
x^2+5x+2k=0
\end{eqnarray}
が共通解を1つだけ持つ。この共通解と定数kを求めよ。ただしk≠-5
【数Ⅰ】【2次関数】2次関数 条件付きの解 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすように、定数mの値の範囲を定めよ。
(1) ２次関数 y=x²+mx+1において、yの値が常に正である。
(2) 放物線 y=x²-2mx+3m-2がy＜0の部分を通らない。
(3) 関数 y=mx²+4x+m-3において、yの値が常に負である。
２次関数 y=x²-mx+m+3のグラフの頂点が第１象限にあるとき、定数mの値の範囲を求めよ。
この動画を見る
次の条件を満たすように、定数mの値の範囲を定めよ。
(1) ２次関数 y=x²+mx+1において、yの値が常に正である。
(2) 放物線 y=x²-2mx+3m-2がy＜0の部分を通らない。
(3) 関数 y=mx²+4x+m-3において、yの値が常に負である。
２次関数 y=x²-mx+m+3のグラフの頂点が第１象限にあるとき、定数mの値の範囲を求めよ。
【数Ⅰ】【2次関数】2次関数 解の個数、連立 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
mは定数とする。放物線 y=x²+(m+3)x+3m+4とx軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数mの値の範囲を求めよ。
(1) x²-mx+1＞0 (2) -x²+mx+2m≦0
次の連立不等式を満たす整数xの値を全て求めよ。
(1) 2x²-x-3＜0 (2) x²+2x＞1
3x²-10x+3＜0 x²-x≦6
この動画を見る
mは定数とする。放物線 y=x²+(m+3)x+3m+4とx軸の共有点の個数を調べよ。
次の2次不等式の解がすべての実数であるとき、定数mの値の範囲を求めよ。
(1) x²-mx+1＞0 (2) -x²+mx+2m≦0
次の連立不等式を満たす整数xの値を全て求めよ。
(1) 2x²-x-3＜0 (2) x²+2x＞1
3x²-10x+3＜0 x²-x≦6
【数Ⅰ】【2次関数】2次関数の解の範囲 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の2次方程式が実数解をもつように、実数ｍの値の範囲を定めよ。
(1) x²+2mx+3=0 (2) x²+mx+m=0
２次方程式 x²-2mx-4m=0 が次の条件を満たすように、定数mの値の範囲を定めよ。
(1) 異なる２つの実数解をもつ (2) 実数解をもたない
次の条件を満たすように、実数mの値の範囲を定めよ。
(1) ２次関数 y=x²-2mx+2m+3 のグラフがｘ軸と共有点をもつ。
(2) ２次関数 y=x²+2mx-m+2 のグラフがｘ軸と共有点をもたない。
この動画を見る
次の2次方程式が実数解をもつように、実数ｍの値の範囲を定めよ。
(1) x²+2mx+3=0 (2) x²+mx+m=0
２次方程式 x²-2mx-4m=0 が次の条件を満たすように、定数mの値の範囲を定めよ。
(1) 異なる２つの実数解をもつ (2) 実数解をもたない
次の条件を満たすように、実数mの値の範囲を定めよ。
(1) ２次関数 y=x²-2mx+2m+3 のグラフがｘ軸と共有点をもつ。
(2) ２次関数 y=x²+2mx-m+2 のグラフがｘ軸と共有点をもたない。
【数Ⅰ】【2次関数】2次関数の点の通過 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たす放物線の方程式を求めよ。
(1) ３点(-4,0),(-2,0),(0,-4)を通る。
(2) 点(2,0)でｘ軸に接し、点(-2,12)を通る。
a,b,cの値を入力すると、関数 y=ax²+bx+c のグラフが表示されるコンピュータソフトがある。
あるa,b,cの値を入力すると、グラフは図のように表示された。
(1) a, b, c, b²-4ac, a+b+c の符号をいえ。
(2) このa,bの値を変えずに、cの値だけを変化させたとき、変わらないものを次の中からすべて選べ。
また、変わらない理由を説明せよ。
① グラフとｘ軸の共有点の個数
② グラフの頂点のｘ座標の符号
③ グラフの頂点のｙ座標の符号
この動画を見る
次の条件を満たす放物線の方程式を求めよ。
(1) ３点(-4,0),(-2,0),(0,-4)を通る。
(2) 点(2,0)でｘ軸に接し、点(-2,12)を通る。
a,b,cの値を入力すると、関数 y=ax²+bx+c のグラフが表示されるコンピュータソフトがある。
あるa,b,cの値を入力すると、グラフは図のように表示された。
(1) a, b, c, b²-4ac, a+b+c の符号をいえ。
(2) このa,bの値を変えずに、cの値だけを変化させたとき、変わらないものを次の中からすべて選べ。
また、変わらない理由を説明せよ。
① グラフとｘ軸の共有点の個数
② グラフの頂点のｘ座標の符号
③ グラフの頂点のｙ座標の符号
【数Ⅰ】【2次関数】2次関数のグラフ応用 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の2次関数のグラフがｘ軸から切り取る線分の長さを求めよ。
(1) y=x²-2x-8 (2) y=x²+6x+7
2次関数 y=x²-4x+2m のグラフとｘ軸の共有点の個数は，定数 m の値によってどのように変わるか。
この動画を見る
次の2次関数のグラフがｘ軸から切り取る線分の長さを求めよ。
(1) y=x²-2x-8 (2) y=x²+6x+7
2次関数 y=x²-4x+2m のグラフとｘ軸の共有点の個数は，定数 m の値によってどのように変わるか。
【数Ⅰ】【2次関数】文字を含む2次方程式 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
aを定数とするとき，次の方程式を解け。
(1) a²x + 1 = a(x + 1)
(2) ax² + (a² - 1)x - a = 0
２つの２次方程式 x² + (m + 3)x + 8 = 0, x² + 5x + 4m = 0 が共通な実数解をもつように
定数ｍの値を定め, その共通な解を求めよ。
この動画を見る
aを定数とするとき，次の方程式を解け。
(1) a²x + 1 = a(x + 1)
(2) ax² + (a² - 1)x - a = 0
２つの２次方程式 x² + (m + 3)x + 8 = 0, x² + 5x + 4m = 0 が共通な実数解をもつように
定数ｍの値を定め, その共通な解を求めよ。
【数Ⅰ】【2次関数】2次関数の決定 ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 y=-3x²+x-1を平行移動した曲線で，頂点が点(-2,3)である。
(2) 放物線 y=x²-3xを平行移動した曲線で，2点 (2,1),(4,5)を通る。
2つの放物線y=x²-3x, y=1/2x²+ax+bの頂点が一致するように,定数a,bの値を定めよ。
(1) 放物線y=x²-3x十4を平行移動した曲線で，点(2, 4)を通り，頂点が直線y=2x+1上にある放物線の方程式を求めよ。
(2) 放物線y=-2x²＋5xを平行移動した曲線で，点(1, -3)を通り，頂点が放物線y＝x²十4上にある放物線の方程式を求めよ。
この動画を見る
次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 y=-3x²+x-1を平行移動した曲線で，頂点が点(-2,3)である。
(2) 放物線 y=x²-3xを平行移動した曲線で，2点 (2,1),(4,5)を通る。
2つの放物線y=x²-3x, y=1/2x²+ax+bの頂点が一致するように,定数a,bの値を定めよ。
(1) 放物線y=x²-3x十4を平行移動した曲線で，点(2, 4)を通り，頂点が直線y=2x+1上にある放物線の方程式を求めよ。
(2) 放物線y=-2x²＋5xを平行移動した曲線で，点(1, -3)を通り，頂点が放物線y＝x²十4上にある放物線の方程式を求めよ。
【数Ⅰ】【2次関数】2次関数の最大と最小条件式付き ※問題文は概要欄
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) 2x+y=1のとき，x²＋y²の最小値を求めよ。
(2) x+2y+3=0のとき，xyの最大値を求めよ。
x≧0, y≧0, x+y=4のとき，xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。
この動画を見る
(1) 2x+y=1のとき，x²＋y²の最小値を求めよ。
(2) x+2y+3=0のとき，xyの最大値を求めよ。
x≧0, y≧0, x+y=4のとき，xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。
福田のおもしろ数学381〜三角形に内接する長方形と円の面積和の最大値
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
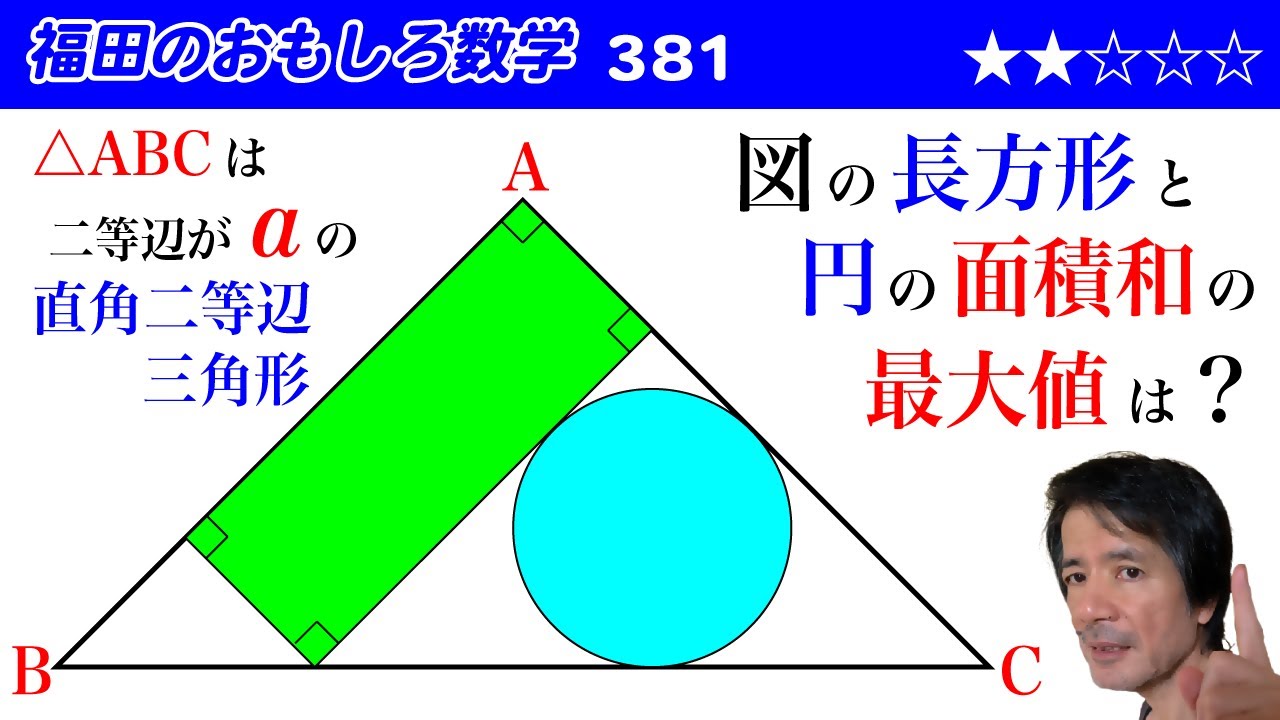
$\triangle$$ABC$は二等辺が$a$の直角二等辺三角形である。また、図のように
三角形の内部に長方形と円を配置する。
図の長方形と円の面積和の最大値は？
この動画を見る
$\triangle$$ABC$は二等辺が$a$の直角二等辺三角形である。また、図のように
三角形の内部に長方形と円を配置する。
図の長方形と円の面積和の最大値は？
2次方程式のこれ解ける？
単元：
#数学(中学生)#中３数学#２次方程式#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。（灘高校 2024）
この動画を見る
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。（灘高校 2024）
高２から東大に挑戦！二次方程式と対数の融合問題！基本がぎゅっと詰まってます【東京大学】【数学 入試問題】
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
2次方程式 x^2-2xloga_b+logb_a=0 が異なる実数解α,βをもち、0<α<1<β となるものとする。このときa,b,1の大きさの順序はどのようなものになるか？
この動画を見る
2次方程式 x^2-2xloga_b+logb_a=0 が異なる実数解α,βをもち、0<α<1<β となるものとする。このときa,b,1の大きさの順序はどのようなものになるか？
2次方程式の解を四捨五入！？あまり見かけない問題。解ける？ #Shorts #ずんだもん #勉強 #数学
単元：
#数Ⅰ#数A#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
m,nを正の整数とする。xについての2次方程式 12x^2-mx+n=0 の2つの実数解を小数第2位で四捨五入して0.3および0.7を得た。m,nを求めよ。
この動画を見る
m,nを正の整数とする。xについての2次方程式 12x^2-mx+n=0 の2つの実数解を小数第2位で四捨五入して0.3および0.7を得た。m,nを求めよ。