 2次関数とグラフ
2次関数とグラフ
 2次関数とグラフ
2次関数とグラフ
【数Ⅰ】【2次関数】不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。
この動画を見る
不等式 x²+9x+18<0 を満たすすべてのxが不等式 x²-4ax+3a<0 を満たすような定数a の値の範囲を求めよ。
【数Ⅰ】【2次関数】aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
この動画を見る
aは正の定数とする。y=|x²-2x|(0≦x≦a)の最大値を求めよ。
【数Ⅰ】【2次関数】(1) y=|x²+2x|のグラフを描け。(2) |x²+2x|=k の実数解の個数を求めよ。

【数Ⅰ】【2次関数】グラフを利用して、次の不等式を解け。(1) |x+1|<2x (2) |x²-4| >-3x

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
この動画を見る
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
【数Ⅰ】【2次関数】x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
この動画を見る
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
【数Ⅰ】【2次関数】x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
この動画を見る
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
【数Ⅰ】【2次関数】次の条件を満たすような定数a の値の範囲を求めよ。(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。他1問

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1<x<0 の範囲にあり、他の解が 2<x<3 の範囲にある。ただし a>0 とする。
この動画を見る
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1<x<0 の範囲にあり、他の解が 2<x<3 の範囲にある。ただし a>0 とする。
【数Ⅰ】【2次関数】a<b<c のとき(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0の2つの解のうち1つは a<x<b の範囲にありもう1つは b<x<c の範囲にあることを示せ

【数Ⅰ】【2次関数】放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
この動画を見る
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
【数Ⅰ】【2次関数】放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
この動画を見る
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
【数Ⅰ】【2次関数】次の関数に最大値・最小値があればそれを求めよ。(1) y=-2x⁴+4x²+3(2) y=(x²-2x)²+4(x²-2x)-1

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
この動画を見る
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
福田の数学〜早稲田大学2025人間科学部第2問〜絶対値の付いた関数の最小

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{2}$
$a\lt b \lt c$を満たす実数の定数に対して、
すべての実数を定義域とする$x$の関数
$f(x)=\vert x-a \vert + \vert x-b \vert + \vert x-c \vert $を定める。
このとき、$5x+4f(x)$の最小値は
$\boxed{ク}a + \boxed{ケ}b + \boxed{コ}c$である。
また、$f(x)$の最小値が$20$で、
$f(c)=28$かつ$f(10)=31$を満たす$a$の値は
$\boxed{サ}$と$\boxed{シ}$である。
ただし、$\boxed{サ} \lt \boxed{シ}$とする。
$2025$年早稲田大学人間科学部過去問題
【中学数学】2次関数の問題~2024年度北海道公立高校入試大問3~【高校受験】
単元:
#数学(中学生)#中3数学#数Ⅰ#2次関数#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
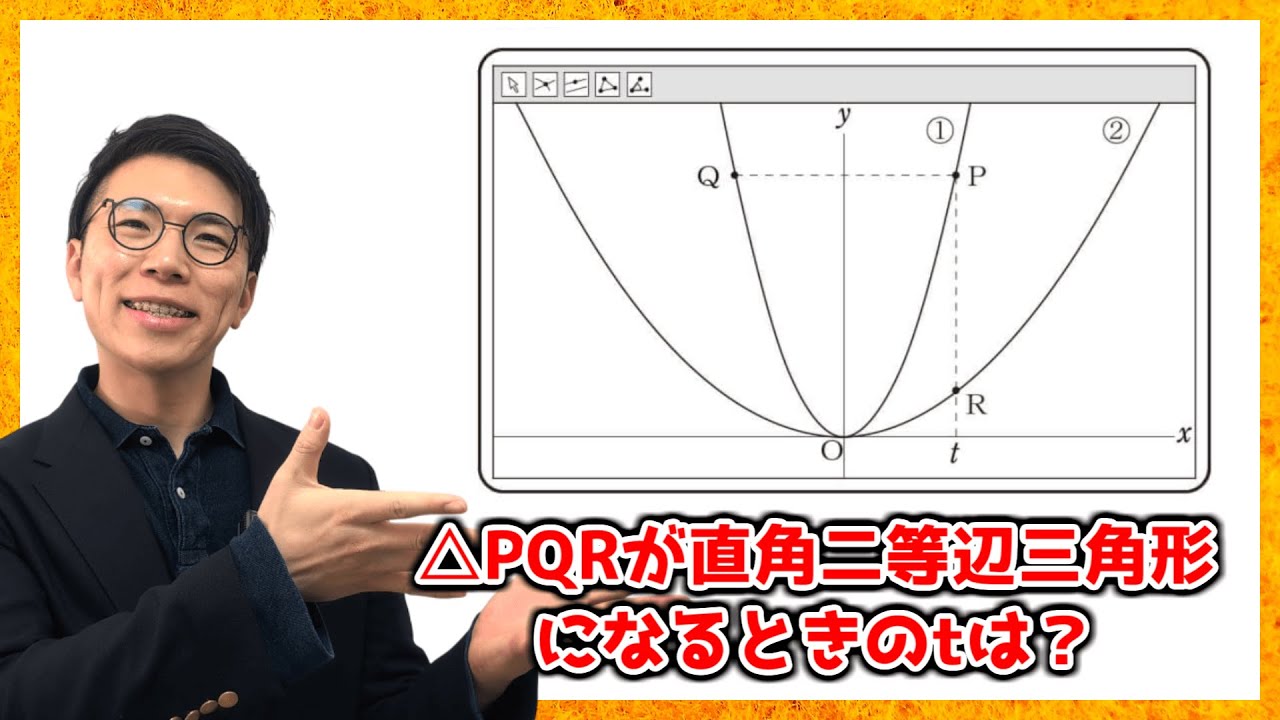
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①,$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$>0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ?△PQRが直角に等辺三角形に見えるときがあるよ?」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
この動画を見る
ユキさんたちのクラスでは、数学の授業で関数のグラフについてコンピュータを使って学習しています。次の問いに答えなさい。
問1 先生が提示した画面1には、関数$y=x^{ 2 }$のグラフと、このグラフ上の2点A、Bを通る直線が表示されています。点Aの$x$座標は3、点Bの$x$座標は-2です。点Oは原点とします。
ユキさんは、画面1を見て、2点A、Bを通る直線の式を求めたいと考え、求め方について、次のような見通しを立てています。
ユキさんの見通し
2点A、Bを通る直線の式を求めるには、2点A、Bの座標がわかれば良い。
次の(1)、(2)に答えなさい。
(1)点Aの$y$座標を求めなさい。
(2)ユキさんの見通しを用いて、2点A、Bを通る直線の式を求めなさい。
問2 △PQRが直角二等辺三角形になる時の$t$の値を求めなさい。
先生が提示した画面2には2つの関数$y=2x^{ 2 }$・・・①,$y=\frac{1}{2}x^{ 2 }$・・・②のグラフが表示されています。①のグラフ上に点Pがあり、点Pの$x$座標は$t$です。点Qは、点Pと$y$軸について対称な点です。また、点Rは、点Pを通り、$y$軸に平行な直線と②のグラフとの交点です。点Oは原点とし、$t$>0とします。
ユキさんたちは、点Pを①のグラフ上で動かすことで、△PQRがどのように変化するかについて、話し合っています。
ユキさん「点Pを動かすと、点Qと点Rも同時に動くね。」
ルイさん「このとき、△PQRはいつでも直角三角形になるね。」
ユキさん「・・・あれ?△PQRが直角に等辺三角形に見えるときがあるよ?」
ルイさん「本当に直角二等辺三角形になるときがあるのかな。」
ユキさん「じゃあ、△PQRが直角二等辺三角形になるときの点Pの座標を求めてみようか。」
ルイさん「点Pの座標を求めるには、$t$の値がわかればいいね。」
△PQRが直角二等辺三角形になるときの$t$の値を求めなさい。
福田のおもしろ数学381〜三角形に内接する長方形と円の面積和の最大値
単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
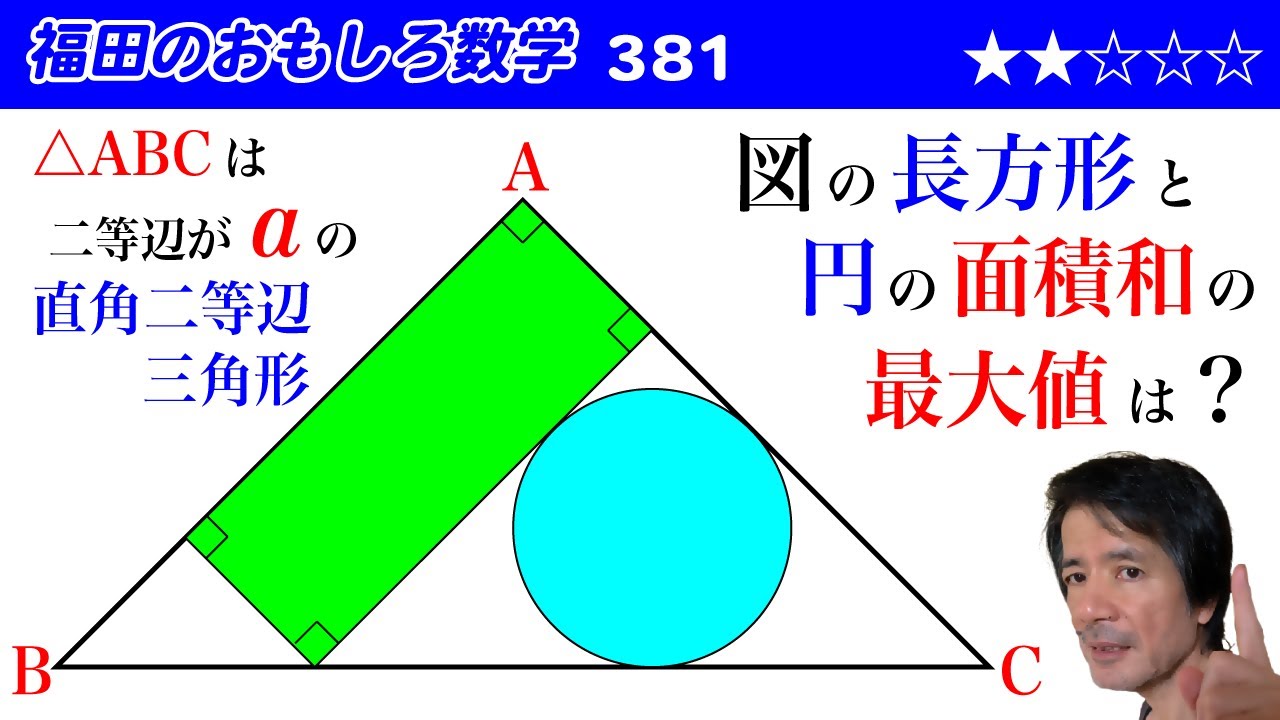
$\triangle$$ABC$は二等辺が$a$の直角二等辺三角形である。また、図のように
三角形の内部に長方形と円を配置する。
図の長方形と円の面積和の最大値は?
この動画を見る
$\triangle$$ABC$は二等辺が$a$の直角二等辺三角形である。また、図のように
三角形の内部に長方形と円を配置する。
図の長方形と円の面積和の最大値は?
【数Ⅰ】【2次関数】2次関数の文章題3 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$AB=6\sqrt{3}、CA=9、∠C=90°$の三角形$ABC$がある。
点$P$は頂点$C$から$A$まで辺$CA$上を毎秒3の速さで進む。
点$Q$は$P$と同時に頂点$B$を出発し、頂点$C$まで辺$BC$上を毎秒$\sqrt{3}$の速さで進む。
この$P,Q$間の距離の最小値を求めよ。
この動画を見る
$AB=6\sqrt{3}、CA=9、∠C=90°$の三角形$ABC$がある。
点$P$は頂点$C$から$A$まで辺$CA$上を毎秒3の速さで進む。
点$Q$は$P$と同時に頂点$B$を出発し、頂点$C$まで辺$BC$上を毎秒$\sqrt{3}$の速さで進む。
この$P,Q$間の距離の最小値を求めよ。
【数Ⅰ】【2次関数】2次関数の文章題2 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
点$P(t,t^2)$は放物線$y=x^2$上の点で、2点$A(-1,1)、B(4,16)$の間にある。このとき、三角形$APB$の面積の最大値を求めよ。
この動画を見る
点$P(t,t^2)$は放物線$y=x^2$上の点で、2点$A(-1,1)、B(4,16)$の間にある。このとき、三角形$APB$の面積の最大値を求めよ。
【数Ⅰ】【2次関数】2次関数の文章題1 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
周囲の長さが24cmである長方形について、次の問いに答えよ。
(1) この長方形の面積の最大値を求めよ。また、そのとき、長方形はどのような形か。
(2) この長方形の対角線を1辺とする正方形の面積の最小値を求めよ。
この動画を見る
周囲の長さが24cmである長方形について、次の問いに答えよ。
(1) この長方形の面積の最大値を求めよ。また、そのとき、長方形はどのような形か。
(2) この長方形の対角線を1辺とする正方形の面積の最小値を求めよ。
【数Ⅰ】【2次関数】2次関数の最大最小場合分け11 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$f(x)=-x^2+2x+2(a\leqq x\leqq a+1)$の最大値を$M(a)$、最小値を$m(a)$とする。
(1)$M(a)$を求め、$b=M(a)$のグラフをかけ
(2)$m(a)$を求め、$b=m(a)$のグラフをかけ
この動画を見る
関数$f(x)=-x^2+2x+2(a\leqq x\leqq a+1)$の最大値を$M(a)$、最小値を$m(a)$とする。
(1)$M(a)$を求め、$b=M(a)$のグラフをかけ
(2)$m(a)$を求め、$b=m(a)$のグラフをかけ
【数Ⅰ】【2次関数】2次関数の最大最小場合分け10 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a$は定数とする。関数$y=x^2-2x+1(a\leqq x\leqq a+1)$について
(1) 最小値を求めよ
(2) 最大値を求めよ
この動画を見る
$a$は定数とする。関数$y=x^2-2x+1(a\leqq x\leqq a+1)$について
(1) 最小値を求めよ
(2) 最大値を求めよ
【数Ⅰ】【2次関数】2次関数の最大最小場合分け9 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$y=x^2-2x+m$の値が$0\leqq x\leqq 3$の範囲で常に負となるように、定数$m$の値の範囲を定めよ
この動画を見る
関数$y=x^2-2x+m$の値が$0\leqq x\leqq 3$の範囲で常に負となるように、定数$m$の値の範囲を定めよ
【数Ⅰ】【2次関数】2次関数の最大最小場合分け8 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a\gt 0$とする。関数$y=ax^2+2ax+b(-2\leqq x\leqq 1)$の最大値が6、最小値が3であるように、定数$a,b$の値を定めよ。
この動画を見る
$a\gt 0$とする。関数$y=ax^2+2ax+b(-2\leqq x\leqq 1)$の最大値が6、最小値が3であるように、定数$a,b$の値を定めよ。
【数Ⅰ】【2次関数】2次関数の最大最小場合分け7 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$y=x^2-2ax-a(0\leqq x\leqq 2)$の最小値が$-2$であるように、定数$a$の値を定めよ。
この動画を見る
関数$y=x^2-2ax-a(0\leqq x\leqq 2)$の最小値が$-2$であるように、定数$a$の値を定めよ。
【数Ⅰ】【2次関数】2次関数の最大最小場合分け6 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a\lt 0$とする。関数$y=-x^2+2ax+3a(0\leqq x\leqq 1)$の最小値が$-11$であるように、定数$a$の値を定めよ。
この動画を見る
$a\lt 0$とする。関数$y=-x^2+2ax+3a(0\leqq x\leqq 1)$の最小値が$-11$であるように、定数$a$の値を定めよ。
【数Ⅰ】【2次関数】2次関数の最大最小場合分け5 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$k$は定数とする。2次関数$y=x^2+2kx+k$の最小値を$m$とする。
(1) $m$は$k$の関数である。$m$を$k$の式で表せ。
(2) $k$の関数$m$の最大値とそのときの$k$の値を求めよ。
この動画を見る
$k$は定数とする。2次関数$y=x^2+2kx+k$の最小値を$m$とする。
(1) $m$は$k$の関数である。$m$を$k$の式で表せ。
(2) $k$の関数$m$の最大値とそのときの$k$の値を求めよ。
【数Ⅰ】【2次関数】2次関数の最大最小場合分け4 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a$を定数とする。
2次関数$y=-x^2+2ax(0\leqq x\leqq 1)$の最大値を$M(a)$とするとき、次の問いに答えよ。
(1) $M(a)$を求めよ
(2) $b=M(a)$のグラフをかけ。
この動画を見る
$a$を定数とする。
2次関数$y=-x^2+2ax(0\leqq x\leqq 1)$の最大値を$M(a)$とするとき、次の問いに答えよ。
(1) $M(a)$を求めよ
(2) $b=M(a)$のグラフをかけ。
【数Ⅰ】【2次関数】2次関数の対称移動3 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線y=2x²-4x+1を、直線y=-2に関して対称移動して得られる放物線の方程式を求めよ。
この動画を見る
放物線y=2x²-4x+1を、直線y=-2に関して対称移動して得られる放物線の方程式を求めよ。
【数Ⅰ】【2次関数】2次関数の対称移動2 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある放物線を、x軸方向にー1、y軸方向にー3だけ平行移動し、さらにx軸に関して対称移動をしたら、放物線y=x²-2x+2に移った。もとの放物線の方程式を求めよ。
この動画を見る
ある放物線を、x軸方向にー1、y軸方向にー3だけ平行移動し、さらにx軸に関して対称移動をしたら、放物線y=x²-2x+2に移った。もとの放物線の方程式を求めよ。
【数Ⅰ】【2次関数】2次関数の対称移動1 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の直線、放物線を、x軸、y軸、原点に関して、それぞれ対称移動して得られる直線、放物線の方程式を求めよ。
(1)y=-x+1
(2)y=2x²+x
(3)y=-x²-x-6
この動画を見る
次の直線、放物線を、x軸、y軸、原点に関して、それぞれ対称移動して得られる直線、放物線の方程式を求めよ。
(1)y=-x+1
(2)y=2x²+x
(3)y=-x²-x-6
【数Ⅰ】【2次関数】2次関数の平行移動4 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線$y=x^2-4x+3$を、次の方向に平行移動して原点を通るようにした放物線の方程式を求めよ。
(1)y軸方向
(2)x軸方向
この動画を見る
放物線$y=x^2-4x+3$を、次の方向に平行移動して原点を通るようにした放物線の方程式を求めよ。
(1)y軸方向
(2)x軸方向
【数Ⅰ】【2次関数】2次関数の平行移動3 ※問題文は概要欄

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の放物線をx軸方向に1、y軸方向に-2だけ平行移動して得られる放物線の方程式を求めよ。
(1)$y=-x^2$
(2)$y=2x^2+4x$
(3)$y=3x^2+x-4$
この動画を見る
次の放物線をx軸方向に1、y軸方向に-2だけ平行移動して得られる放物線の方程式を求めよ。
(1)$y=-x^2$
(2)$y=2x^2+4x$
(3)$y=3x^2+x-4$
