2次方程式と2次不等式
2次方程式と2次不等式
よく間違える二次関数の変域
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$-1\leqq x^2\leqq 2のとき、x^2の範囲をもとめよ$
この動画を見る
$-1\leqq x^2\leqq 2のとき、x^2の範囲をもとめよ$
2次方程式の応用 （高校数学）
単元：
#２次関数#2次方程式と2次不等式#2次関数とグラフ
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式 $(x-l) (x-2) -(x-k) =0$ の解を $α,β(α<β)$ とするとき、$α,β,l,2, k$ を小さい順に並べよ
この動画を見る
2次方程式 $(x-l) (x-2) -(x-k) =0$ の解を $α,β(α<β)$ とするとき、$α,β,l,2, k$ を小さい順に並べよ
2次方程式の応用 （高校数学）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式$(x-1)(x-2)-(x-k)=0の解を\mathit{α ,β}(\mathit{α}<\mathit{β})とするとき
\mathit{α,β},1,2,kを小さい順に並べよ。(ただし、1<\mathit{k}<2$)
この動画を見る
2次方程式$(x-1)(x-2)-(x-k)=0の解を\mathit{α ,β}(\mathit{α}<\mathit{β})とするとき
\mathit{α,β},1,2,kを小さい順に並べよ。(ただし、1<\mathit{k}<2$)
福田の数学〜中央大学2024経済学部第1問(1)〜絶対値の付いた2次不等式の解
連立方程式 2通りで解説！！ コメント欄に訂正あり。
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の連立方程式を解け
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy=2 \\
yz=6 \\
zx=3
\end{array}
\right.
\end{eqnarray}$
福田のおもしろ数学189〜xyzの関係式からzの最大最小を決定する
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x, \, y, \, z$ は実数で
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z = 1 \\
x^2 + y^2 + z^2 = 3
\end{array}
\right.
\end{eqnarray}$
のとき、$z$ の最大値と最小値、そのときの $x, \, y$ を求めよ。
この動画を見る
$x, \, y, \, z$ は実数で
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z = 1 \\
x^2 + y^2 + z^2 = 3
\end{array}
\right.
\end{eqnarray}$
のとき、$z$ の最大値と最小値、そのときの $x, \, y$ を求めよ。
【数学受験組の実力チェック】三平方の定理と二次方程式の解の公式を証明せよ【東大・早稲田・国立志望】
単元：
#数学(中学生)#中３数学#２次方程式#数Ⅰ#２次関数#三平方の定理#2次方程式と2次不等式#数学(高校生)
指導講師：
Morite2 English Channel
問題文全文(内容文)：
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう！
この動画を見る
数学系YouTuberの鈴木貫太郎先生が「三平方の定理」と「二次方程式の解の公式」を証明します。
考え方を学んで、復習の参考にしましょう！
福田の数学〜名古屋大学2024年文系第2問〜放物線と直線の関係
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ $t$を0でない実数として、$x$の関数$y$=$-x^2$+$tx$+$t$ のグラフを$C$とする。
(1)$C$上において$y$座標が最大となる点Pの座標を求めよ。
(2)Pと点O(0,0)を通る直線を$l$とする。$l$と$C$がP以外の共有点Qを持つために$t$が満たすべき条件を求めよ。また、そのとき、点Qの座標を求めよ。
(3)$t$は(2)の条件を満たすとする。A(-1,-2)として、$X$=$\displaystyle\frac{1}{4}t^2$+$t$ とおくとき、AP$^2$－AQ$^2$を$X$で表せ。また、AP<AQとなるために$t$が満たすべき条件を求めよ。
この動画を見る
$\Large\boxed{2}$ $t$を0でない実数として、$x$の関数$y$=$-x^2$+$tx$+$t$ のグラフを$C$とする。
(1)$C$上において$y$座標が最大となる点Pの座標を求めよ。
(2)Pと点O(0,0)を通る直線を$l$とする。$l$と$C$がP以外の共有点Qを持つために$t$が満たすべき条件を求めよ。また、そのとき、点Qの座標を求めよ。
(3)$t$は(2)の条件を満たすとする。A(-1,-2)として、$X$=$\displaystyle\frac{1}{4}t^2$+$t$ とおくとき、AP$^2$－AQ$^2$を$X$で表せ。また、AP<AQとなるために$t$が満たすべき条件を求めよ。
２次不等式はこの手順通りに考えれば解けちゃう!? #数学 #高校数学 #不等式
【高校数学】２次不等式はこれでマスター！この手順通りに考えれば解けちゃう【数学のコツ】
複雑な2次方程式。あれ使え。桐光学園
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$2(x-1)^2-4\sqrt3(x-1)+1=0$
2024桐光学園高等学校
この動画を見る
方程式を解け
$2(x-1)^2-4\sqrt3(x-1)+1=0$
2024桐光学園高等学校
一手間加えるだけで美味しい方程式
【その手があったか…！】：因数分解への応用（その5）～中学からの二次方程式
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2次方程式の解の公式を用いて
$ px^2+(2p-1)x-(4p-1)$を因数分解せよ.
ただし,$ p\neq 0$とする.
この動画を見る
2次方程式の解の公式を用いて
$ px^2+(2p-1)x-(4p-1)$を因数分解せよ.
ただし,$ p\neq 0$とする.
2次方程式 3通りで解説！！ 2024日比谷高校
単元：
#数Ⅰ#大学入試過去問(数学)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$(x-1)^2-4(x-2)^2=0$
2024日比谷高等学校
この動画を見る
方程式を解け
$(x-1)^2-4(x-2)^2=0$
2024日比谷高等学校
福田のおもしろ数学085〜不等式を満たす自然数の組合せ
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a$＜$b$＜$c$を満たす正の整数の組($a$,$b$,$c$)であって、
$a^2$－$20005a$＞$b^2$－$20005b$＞$c^2$－$20005c$
が成り立つものはいくつあるか。
この動画を見る
$a$＜$b$＜$c$を満たす正の整数の組($a$,$b$,$c$)であって、
$a^2$－$20005a$＞$b^2$－$20005b$＞$c^2$－$20005c$
が成り立つものはいくつあるか。
意外と間違える！？二次方程式 2024京都府
単元：
#数Ⅰ#大学入試過去問(数学)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$8x^2=22x$
2024京都府
この動画を見る
方程式を解け
$8x^2=22x$
2024京都府
知っていれば一瞬！！2次方程式と解と式の関係 2024早稲田実業
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$3x^2-4x-2=0$の2つの解をa,bとする。
$(3a^2-4a+2)(6b^2-8b)=?$
2024早稲田実業学校
この動画を見る
$3x^2-4x-2=0$の2つの解をa,bとする。
$(3a^2-4a+2)(6b^2-8b)=?$
2024早稲田実業学校
二次方程式の解が１つ 灘高校2024
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
xの二次方程式
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値をすべて求めよ
灘高等学校2024
この動画を見る
xの二次方程式
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値をすべて求めよ
灘高等学校2024
ルートを含む二次方程式の計算 2024早稲田本庄最初の一問
単元：
#数Ⅰ#数と式#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$(\sqrt 5 + \sqrt 3 )x^2+2 \sqrt 3x - \sqrt 5+ \sqrt 3= 0$を解け
2024早稲田大学 本庄高等学院
この動画を見る
$(\sqrt 5 + \sqrt 3 )x^2+2 \sqrt 3x - \sqrt 5+ \sqrt 3= 0$を解け
2024早稲田大学 本庄高等学院
二次方程式の解と確率 2024立教新座
単元：
#数Ⅰ#数A#２次関数#場合の数と確率#2次方程式と2次不等式#確率#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
さいころを3回続けて投げるとき、1回目、2回目、3回目に出た目の数をそれぞれa,b,cとする。
2次方程式$ax^2+bx+c=0$について2つの解が-2、-3となる確率を求めよ
2024立教新座高等学校
この動画を見る
さいころを3回続けて投げるとき、1回目、2回目、3回目に出た目の数をそれぞれa,b,cとする。
2次方程式$ax^2+bx+c=0$について2つの解が-2、-3となる確率を求めよ
2024立教新座高等学校
2024年の2次方程式
ちょっと変わった2次方程式
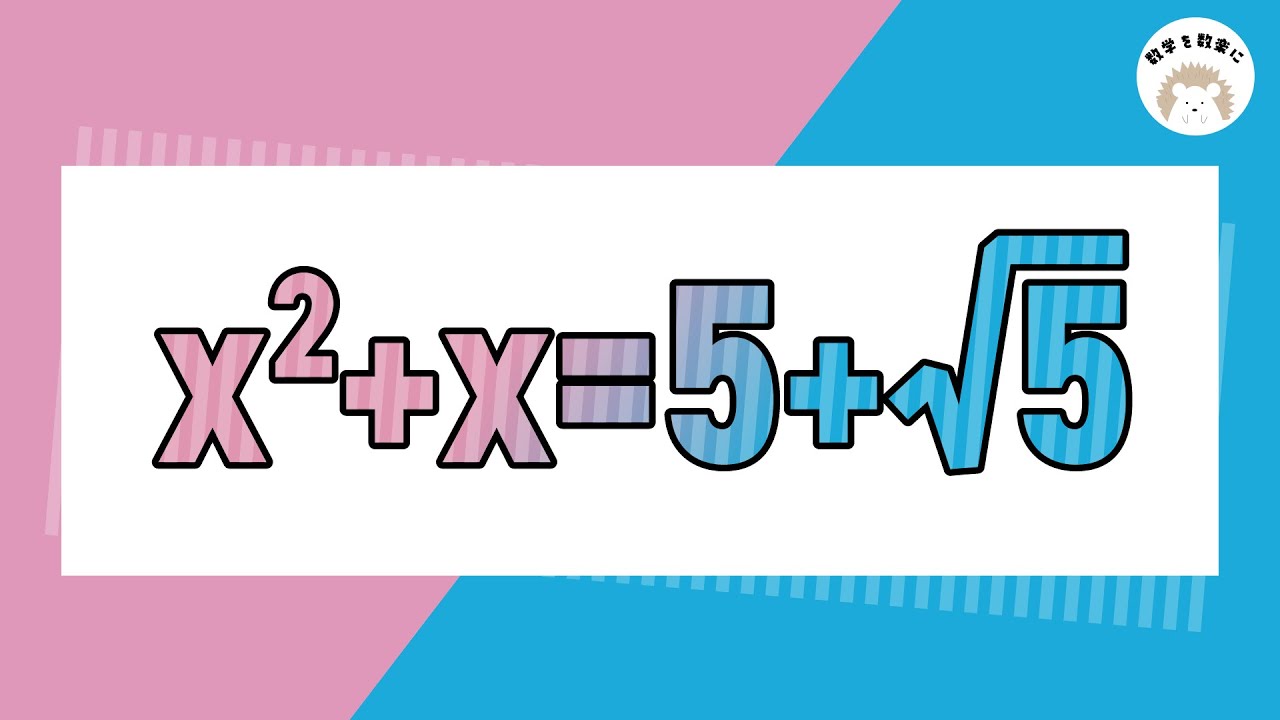
君はどうやって解く？ 3通りで解説 二次方程式の計算 八王子東
二次方程式の解が２つの整数 戸山
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
xの2次方程式$x^2+ax-8=0$の2つの解がともに整数であるとき、aの値をすべて求めよ。
戸山高等学校
この動画を見る
xの2次方程式$x^2+ax-8=0$の2つの解がともに整数であるとき、aの値をすべて求めよ。
戸山高等学校
４次関数の最小値
4次方程式
数学どうにかしたい人へ
単元：
#数Ⅰ#数A#数Ⅱ#数と式#２次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#一次不等式（不等式・絶対値のある方程式・不等式）#集合と命題（集合・命題と条件・背理法）#2次方程式と2次不等式#2次関数とグラフ#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#データの分析#整数の性質#場合の数#確率#三角形の辺の比（内分・外分・二等分線）#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和（等差・等比・階差・Σ）#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数（分数関数・無理関数・逆関数と合成関数）#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化（グラフ・最大最小・方程式・不等式）#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体（オイラーの法則）#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
福田の数学〜虚数係数の2次方程式の解き方〜明治大学2023年全学部統一ⅠⅡＡＢ第1問(2)〜
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$
(2)$k$を実数とする。$x$についての方程式
$x^2$-(4-3$i$)$x$+(4-$ki$)=0
を満たす実数$x$があるとき、$k$=$\boxed{\ \ キ\ \ }$である。このとき、上の等式を満たす$x$の値は2つあり、$\boxed{\ \ ク\ \ }$と$\boxed{\ \ ケ\ \ }$-$\boxed{\ \ コ\ \ }$$i$ である。ただし、$i$を虚数単位とする。
この動画を見る
$\Large{\boxed{1}}$
(2)$k$を実数とする。$x$についての方程式
$x^2$-(4-3$i$)$x$+(4-$ki$)=0
を満たす実数$x$があるとき、$k$=$\boxed{\ \ キ\ \ }$である。このとき、上の等式を満たす$x$の値は2つあり、$\boxed{\ \ ク\ \ }$と$\boxed{\ \ ケ\ \ }$-$\boxed{\ \ コ\ \ }$$i$ である。ただし、$i$を虚数単位とする。
引くばか 二次方程式の応用 昭和学院秀英
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式$2x^2-5x+c=0$の2つの解の比が2:3である。
定数cの値を求めよ。
昭和学院秀英高等学校
この動画を見る
2次方程式$2x^2-5x+c=0$の2つの解の比が2:3である。
定数cの値を求めよ。
昭和学院秀英高等学校
いきなり展開したら負け！東邦大附属東邦
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式を解け
$(100 - x)(101 -x) = 104-x$
東邦大学付属東邦高等学校
この動画を見る
2次方程式を解け
$(100 - x)(101 -x) = 104-x$
東邦大学付属東邦高等学校