 三角比(三角比・拡張・相互関係・単位円)
三角比(三角比・拡張・相互関係・単位円)
 三角比(三角比・拡張・相互関係・単位円)
三角比(三角比・拡張・相互関係・単位円)
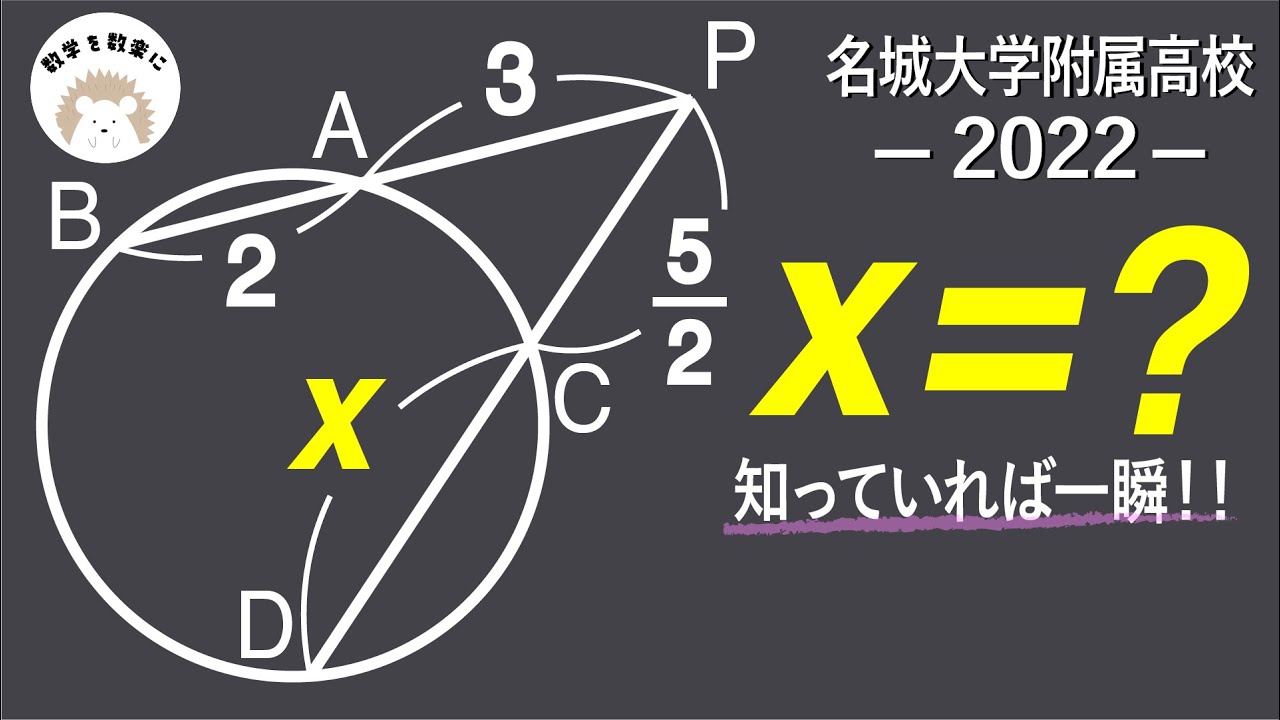
知ってれば一瞬!! 名城大学附属2022入試問題解説31問目
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
*図は動画内参照
2022名城大学附属高等学校
この動画を見る
x=?
*図は動画内参照
2022名城大学附属高等学校
円周角 中央大杉並 推薦 2022入試問題解説27問目

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle MBN = ?$
*図は動画内参照
2022中央大学杉並高等学校
この動画を見る
$\angle MBN = ?$
*図は動画内参照
2022中央大学杉並高等学校
cosで合成 2通りで解説!

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2}cosθ+\frac{\sqrt 3}{2} sinθ$を
$▢cos(θ - ○)$の形に直せ
この動画を見る
$\frac{1}{2}cosθ+\frac{\sqrt 3}{2} sinθ$を
$▢cos(θ - ○)$の形に直せ
高校入試レベルだよ
sin sin sin sin sin sin sin sin sin sin sin sin
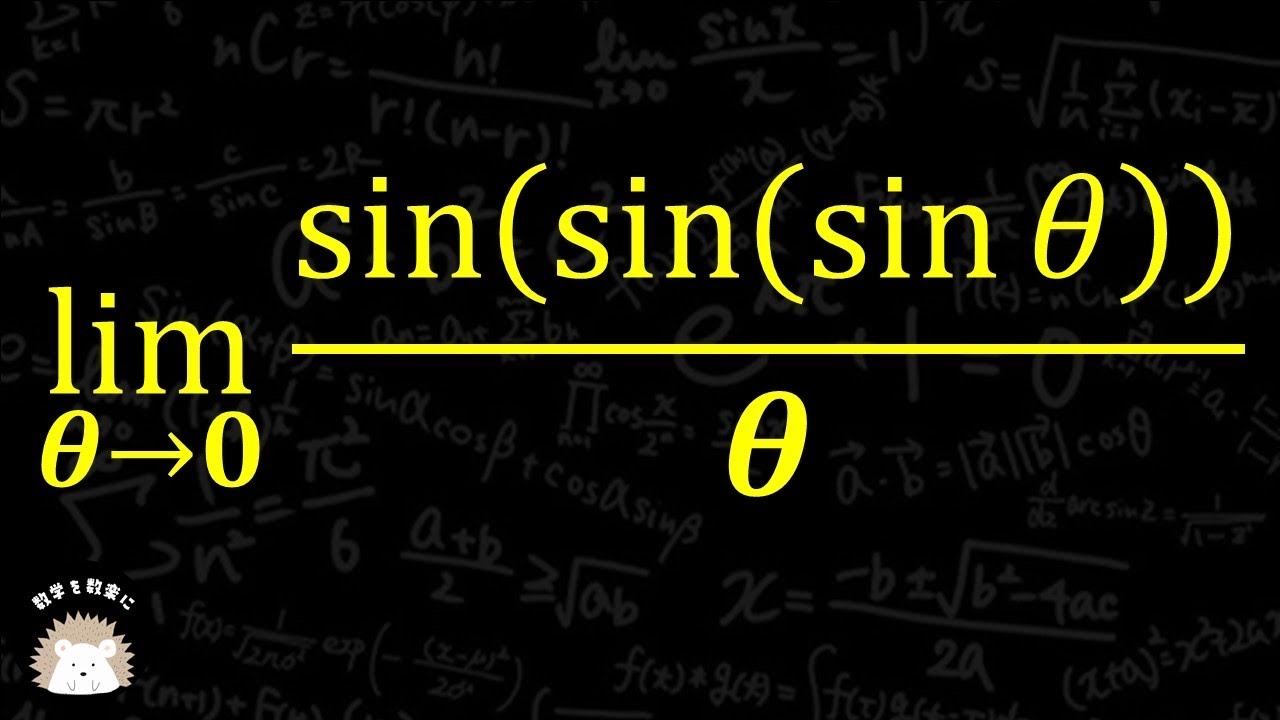
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\displaystyle \lim_{ θ \to 0 } \frac{sin(sin(sin θ))}{θ}
$
この動画を見る
$
\displaystyle \lim_{ θ \to 0 } \frac{sin(sin(sin θ))}{θ}
$
図形的イメージ
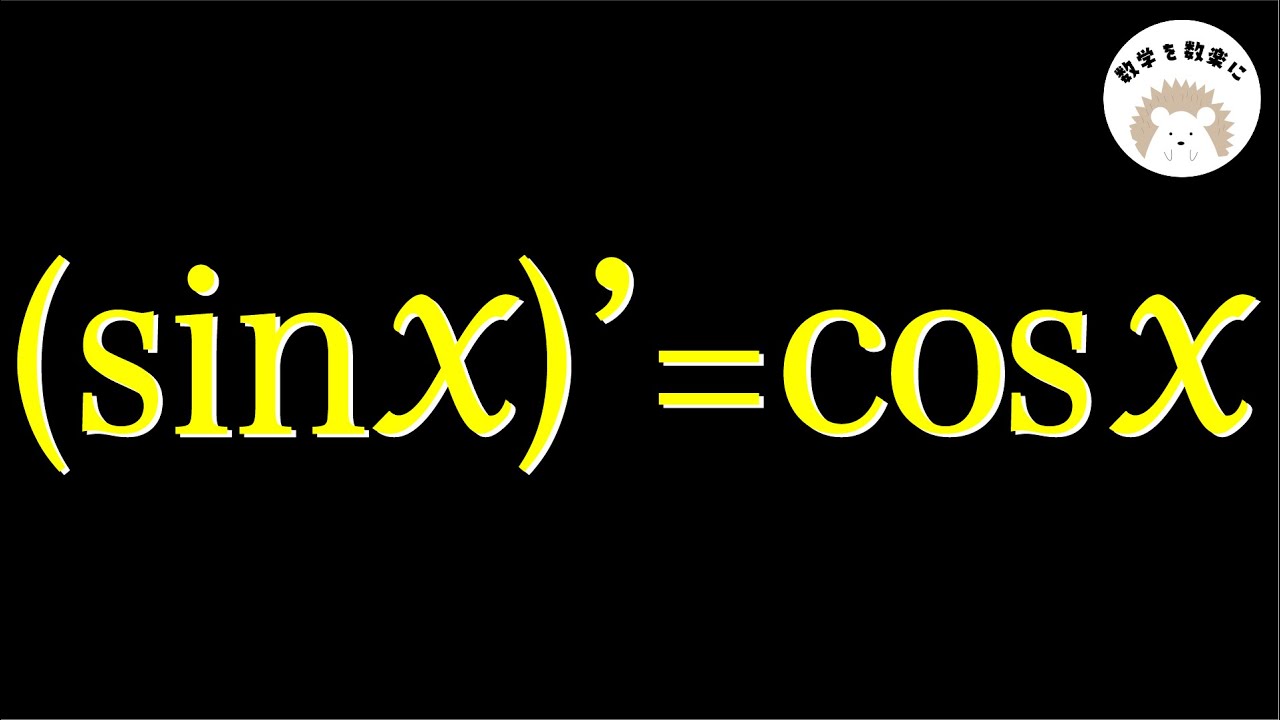
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(sinx)' = cosx
この動画を見る
(sinx)' = cosx
福田の共通テスト解答速報〜2022年共通テスト数学IA問題1[2]。三角比を用いた測量の問題。

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第1問\ [2] 太郎さんは花子さんは、キャンプ場のガイドブックにある地図を見ながら、
後のように話している。
太郎:キャンプ場の地点Aから山頂Bを見上げる角度はどれくらいかな。
花子:地図アプリを使って、地点Aと山頂Bを含む断面図を調べたら、
図1(※動画参照)のようになったよ。点Cは、山頂Bから地点Aを通る水平面に下ろした
垂線とその水平面との交点のことだよ。
太郎:図1の角度\thetaは、AC,BCの長さを定規で測って、
三角比の表を用いて調べたら16°だったよ。
花子:本当に16°なの?図1の鉛直方向の縮尺と水平方向の縮尺は等しい
のかな?
図1の$\theta$はちょうど16°であったとする。しかし、図1の縮尺は、水平方向が$\frac{1}{100000}$
であるのに対して鉛直方向は$\frac{1}{25000}$であった。
実際にキャンプ場の地点Aから山頂Bを見上げる角である$\angle BAC$を考えると、
$\tan\angle BACは\boxed{\ \ コ\ \ }.\boxed{\ \ サシス\ \ }$である。
したがって、$\angle BAC$の大きさは$\boxed{セ}$、ただし、目の高さは無視して考えるものとする。
$\boxed{セ}$の解答群
⓪3°より大きく4°より小さい ①ちょうど4°である ②4°より大きく5°より小さい
③ちょうど16°である ④48°より大きく49°より小さい ⑤ちょうど49°である
⑥49°より大きく50°より小さい ⑦63°より大きく64°より小さい ⑧ちょうど64°である
⑨64°より大きく65°より小さい
2022共通テスト数学過去問
この動画を見る
第1問\ [2] 太郎さんは花子さんは、キャンプ場のガイドブックにある地図を見ながら、
後のように話している。
太郎:キャンプ場の地点Aから山頂Bを見上げる角度はどれくらいかな。
花子:地図アプリを使って、地点Aと山頂Bを含む断面図を調べたら、
図1(※動画参照)のようになったよ。点Cは、山頂Bから地点Aを通る水平面に下ろした
垂線とその水平面との交点のことだよ。
太郎:図1の角度\thetaは、AC,BCの長さを定規で測って、
三角比の表を用いて調べたら16°だったよ。
花子:本当に16°なの?図1の鉛直方向の縮尺と水平方向の縮尺は等しい
のかな?
図1の$\theta$はちょうど16°であったとする。しかし、図1の縮尺は、水平方向が$\frac{1}{100000}$
であるのに対して鉛直方向は$\frac{1}{25000}$であった。
実際にキャンプ場の地点Aから山頂Bを見上げる角である$\angle BAC$を考えると、
$\tan\angle BACは\boxed{\ \ コ\ \ }.\boxed{\ \ サシス\ \ }$である。
したがって、$\angle BAC$の大きさは$\boxed{セ}$、ただし、目の高さは無視して考えるものとする。
$\boxed{セ}$の解答群
⓪3°より大きく4°より小さい ①ちょうど4°である ②4°より大きく5°より小さい
③ちょうど16°である ④48°より大きく49°より小さい ⑤ちょうど49°である
⑥49°より大きく50°より小さい ⑦63°より大きく64°より小さい ⑧ちょうど64°である
⑨64°より大きく65°より小さい
2022共通テスト数学過去問
全米をsin撼させた問題です。
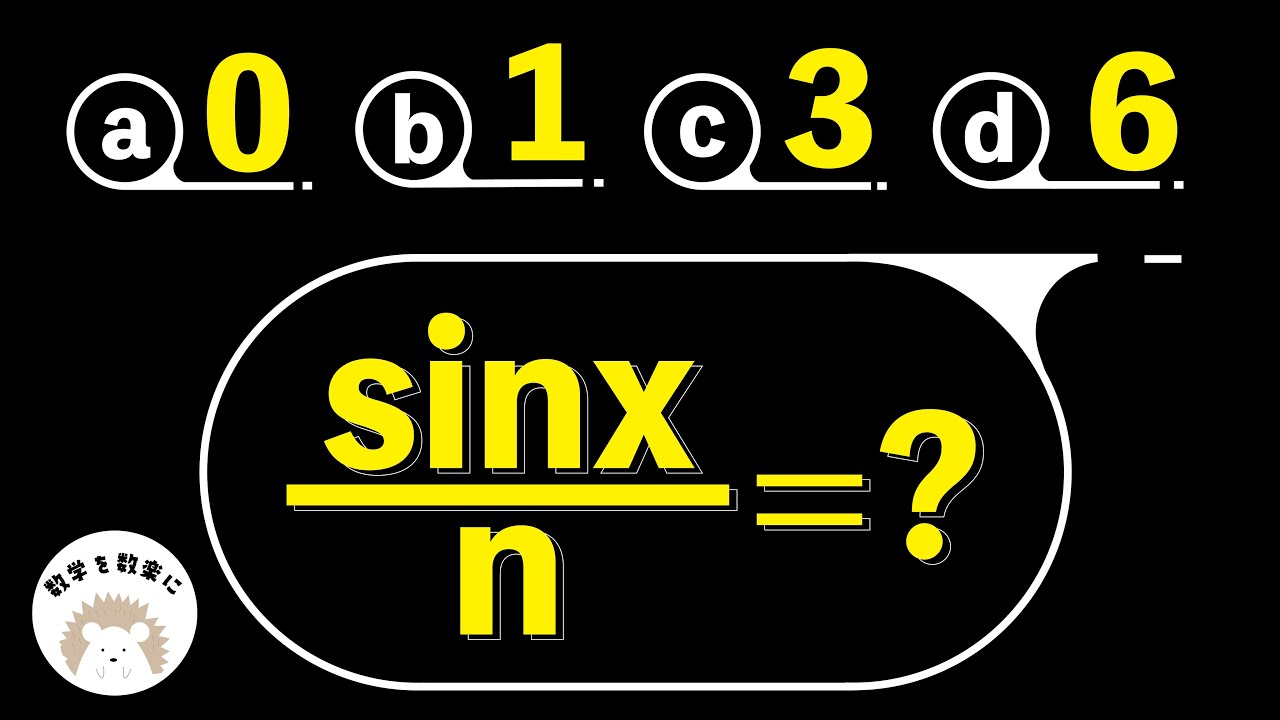
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{sinx}{n} = ?$
(a) 0
(b) 1
(c) 3
(d) 6
この動画を見る
$\frac{sinx}{n} = ?$
(a) 0
(b) 1
(c) 3
(d) 6
福田の共通テスト直前演習〜2021年共通テスト数学IA問題1[2]。三角比に関する問題。

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$[2]右の図のように、$\triangle ABC$の外側に辺AB,BC,CAをそれぞれ1辺とする
正方形ADEB,BFGC,CHIAをかき、2点EとF、GとH、IとDをそれぞれ
線分で結んだ図形を考える。以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, \angle BCA=C$ とする。
(1)$b=6, c=5, \cos A=\frac{3}{5}$のとき、$\sin A=\frac{\boxed{セ}}{\boxed{ソ}}$であり、
$\triangle ABC$の面積は$\boxed{タチ}$、$\triangle AID$の面積は$\boxed{ツテ}$である。
(2)正方形BFGC,CHIA,ADEBの面積をそれぞれS_1,S_2,S_3とする。
このとき、$S_1-S_2-S_3$ は
・$0° \lt A \lt 90°$のとき$\boxed{ト}$ ・$A=90°$のとき$\boxed{ナ}$
・$90° \lt A \lt 180°$のとき$\boxed{ニ}$
$\boxed{ト}~\boxed{ニ}$の解答群
⓪0である ①正の値である ②負の値である ③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{ヌ}$である。
$\boxed{ヌ}$の解答群
⓪$a \lt b \lt c$ならば$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば$T_1 \lt T_2 \lt T_3$
②Aが鈍角ならば$T_1 \lt T_2$ かつ$T_1 \lt T_3$
③$a,b,c$の値に関係なく、$T_1 = T_2 = T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さいもの
を求める。$0° \lt A \lt 90°$のとき、$ID \boxed{ネ} BC$であり、
$(\triangle AID$の外接円の半径)$\boxed{ノ}(\triangle ABCの外接円の半径)$
であるから、外接円の半径が最も小さい三角形は
$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{ハ}$である。
$0° \lt A \lt B \lt 90° \lt C$のとき、$\boxed{ヒ}$である。
$\boxed{ネ}、\boxed{ノ}$の解答群
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{ハ}、\boxed{ヒ}$の解答群
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト数学過去問
この動画を見る
${\Large\boxed{1}}$[2]右の図のように、$\triangle ABC$の外側に辺AB,BC,CAをそれぞれ1辺とする
正方形ADEB,BFGC,CHIAをかき、2点EとF、GとH、IとDをそれぞれ
線分で結んだ図形を考える。以下において
$BC=a, CA=b, AB=c$
$\angle CAB=A, \angle ABC=B, \angle BCA=C$ とする。
(1)$b=6, c=5, \cos A=\frac{3}{5}$のとき、$\sin A=\frac{\boxed{セ}}{\boxed{ソ}}$であり、
$\triangle ABC$の面積は$\boxed{タチ}$、$\triangle AID$の面積は$\boxed{ツテ}$である。
(2)正方形BFGC,CHIA,ADEBの面積をそれぞれS_1,S_2,S_3とする。
このとき、$S_1-S_2-S_3$ は
・$0° \lt A \lt 90°$のとき$\boxed{ト}$ ・$A=90°$のとき$\boxed{ナ}$
・$90° \lt A \lt 180°$のとき$\boxed{ニ}$
$\boxed{ト}~\boxed{ニ}$の解答群
⓪0である ①正の値である ②負の値である ③正の値も負の値もとる
(3)$\triangle AID,\triangle BEF,\triangle CGH$の面積をそれぞれ$T_1,T_2,T_3$とする。
このとき、$\boxed{ヌ}$である。
$\boxed{ヌ}$の解答群
⓪$a \lt b \lt c$ならば$T_1 \gt T_2 \gt T_3$
①$a \lt b \lt c$ならば$T_1 \lt T_2 \lt T_3$
②Aが鈍角ならば$T_1 \lt T_2$ かつ$T_1 \lt T_3$
③$a,b,c$の値に関係なく、$T_1 = T_2 = T_3$
(4)$\triangle ABC,\triangle AID,\triangle BEF,\triangle CGH$のうち、外接円の半径が最も小さいもの
を求める。$0° \lt A \lt 90°$のとき、$ID \boxed{ネ} BC$であり、
$(\triangle AID$の外接円の半径)$\boxed{ノ}(\triangle ABCの外接円の半径)$
であるから、外接円の半径が最も小さい三角形は
$0° \lt A \lt B \lt C \lt 90°$のとき、$\boxed{ハ}$である。
$0° \lt A \lt B \lt 90° \lt C$のとき、$\boxed{ヒ}$である。
$\boxed{ネ}、\boxed{ノ}$の解答群
⓪$\lt$ ①$=$ ②$\gt$
$\boxed{ハ}、\boxed{ヒ}$の解答群
⓪$\triangle ABC$ ①$\triangle AID$ ②$\triangle BEF$ ③$\triangle CGH$
2021共通テスト数学過去問
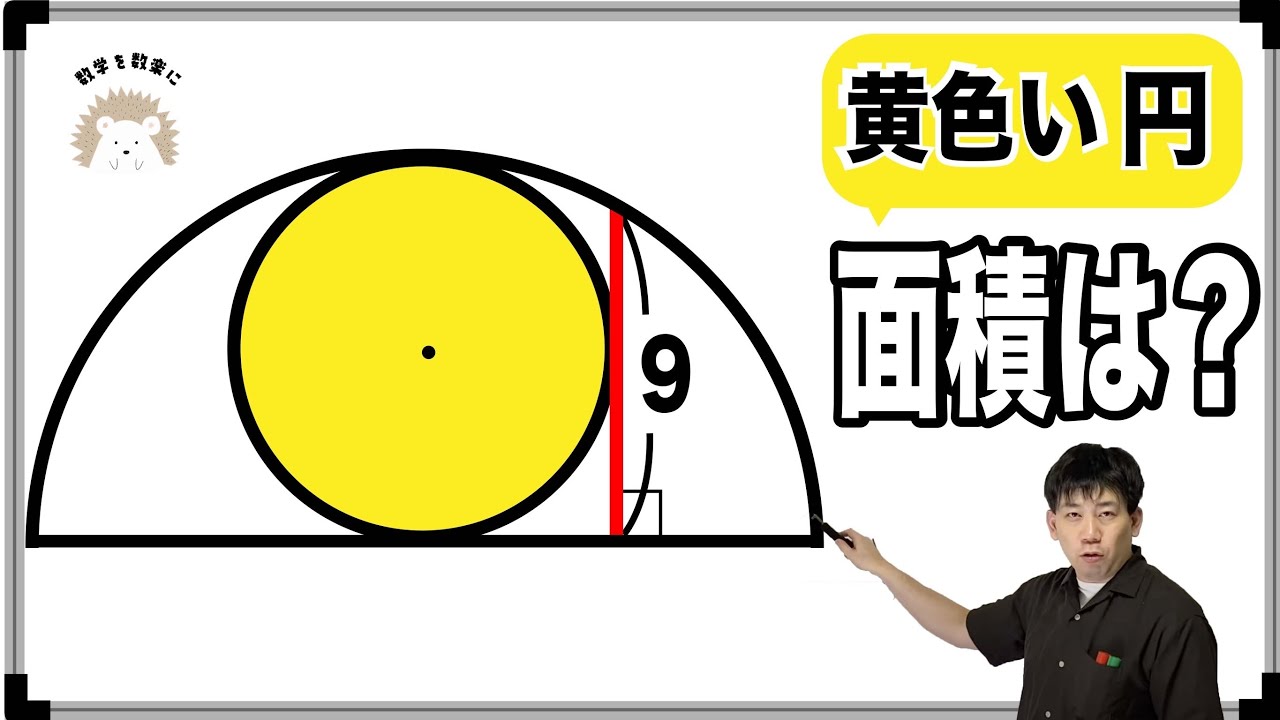
半円と円
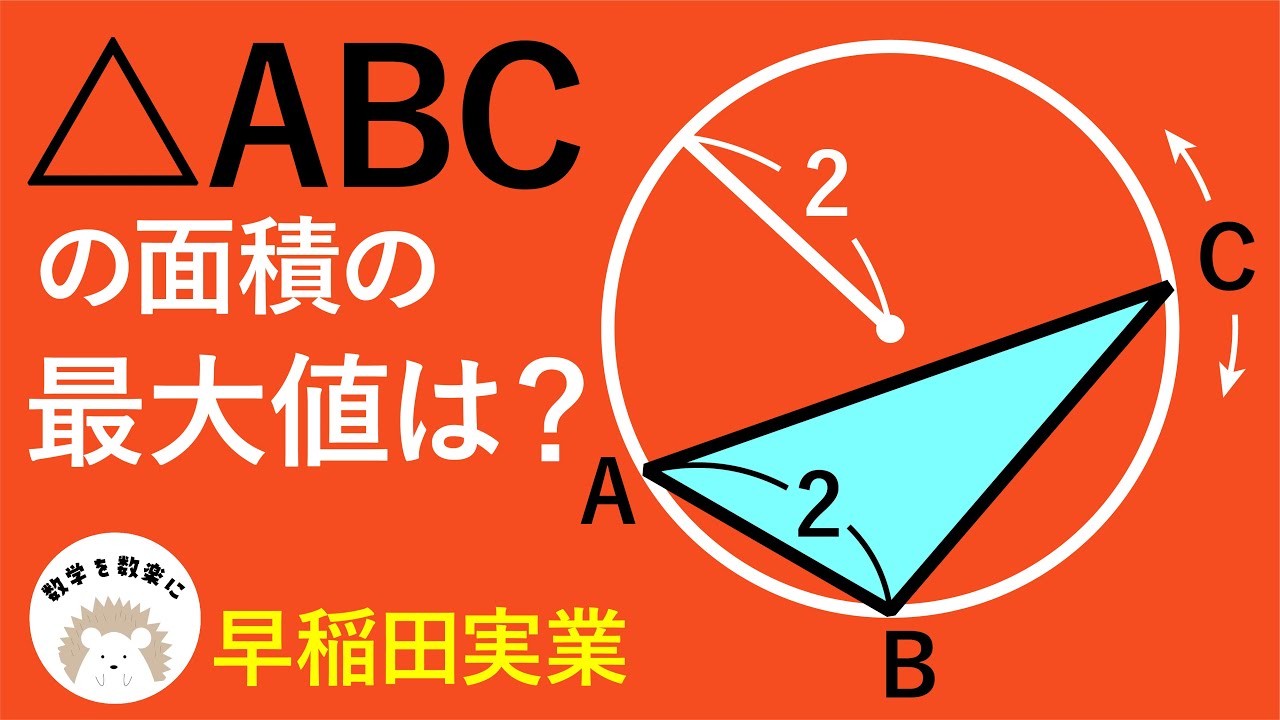
三角形の面積の最大値 早稲田実業
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCの面積の最大値=?
*図は動画内参照
早稲田実業学校
この動画を見る
△ABCの面積の最大値=?
*図は動画内参照
早稲田実業学校
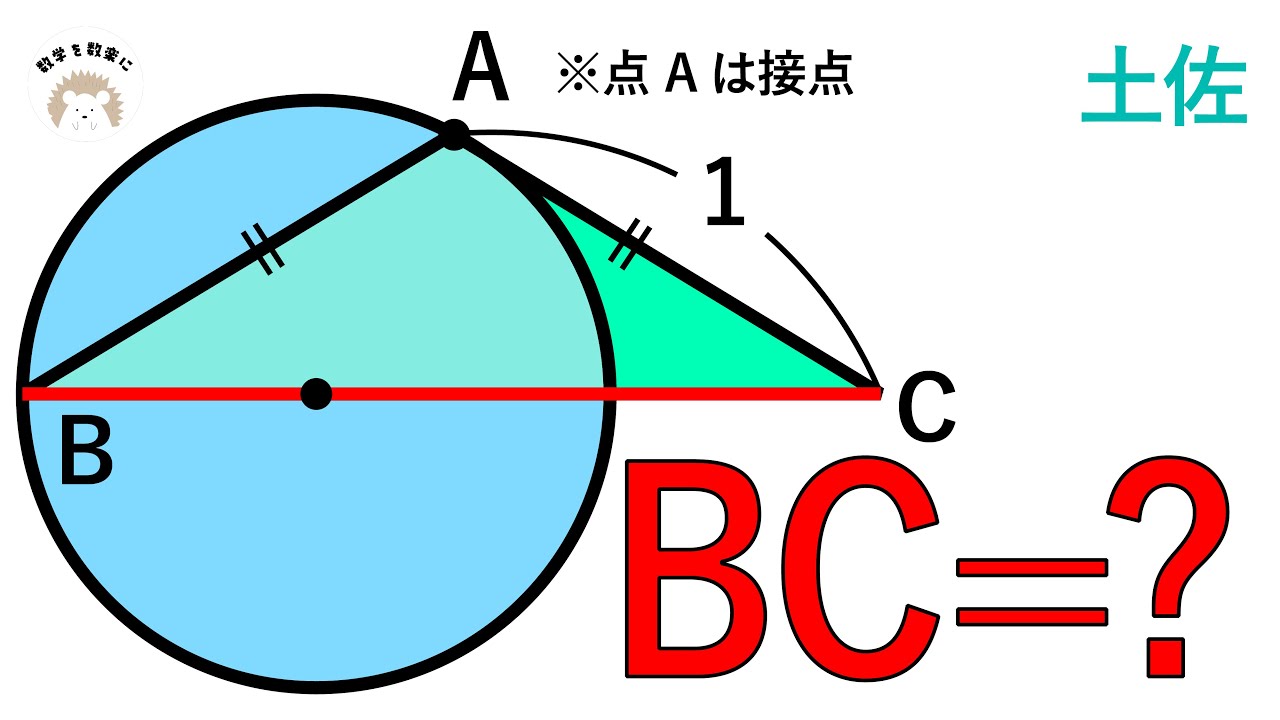
円と二等辺三角形 土佐高校
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BC=?
*図は動画内参照
土佐高等学校(改)
この動画を見る
BC=?
*図は動画内参照
土佐高等学校(改)
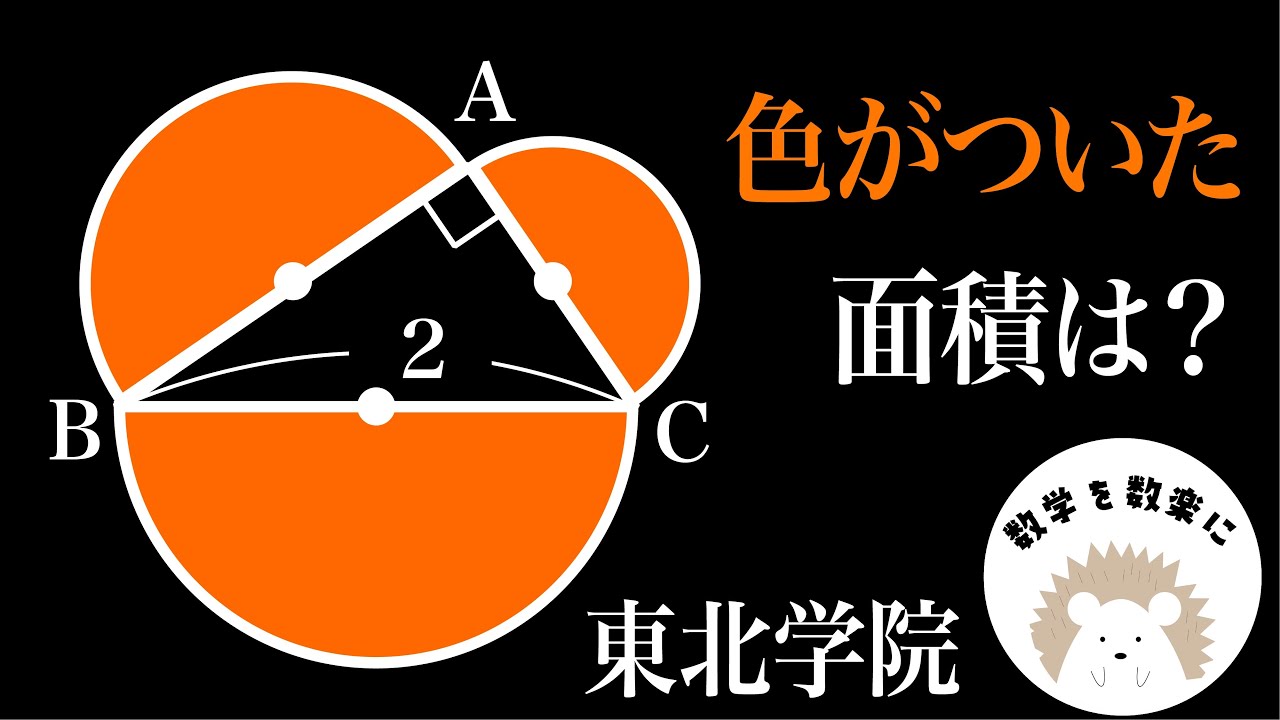
3つの半円の面積の和 東北学院
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
3つの半円の面積の和=?
*図は動画内参照
東北学院高等学校
この動画を見る
3つの半円の面積の和=?
*図は動画内参照
東北学院高等学校
これ便利すぎ

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\sin 330^{ \circ }=-\displaystyle \frac{1}{2}$
面白い有名角の覚え方紹介動画です
この動画を見る
$\sin 330^{ \circ }=-\displaystyle \frac{1}{2}$
面白い有名角の覚え方紹介動画です
【数Ⅰ】三角比総まとめ【三角比の基本をざっくりと振り返ろう】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
三角比の基本に関して解説していきます.
この動画を見る
三角比の基本に関して解説していきます.
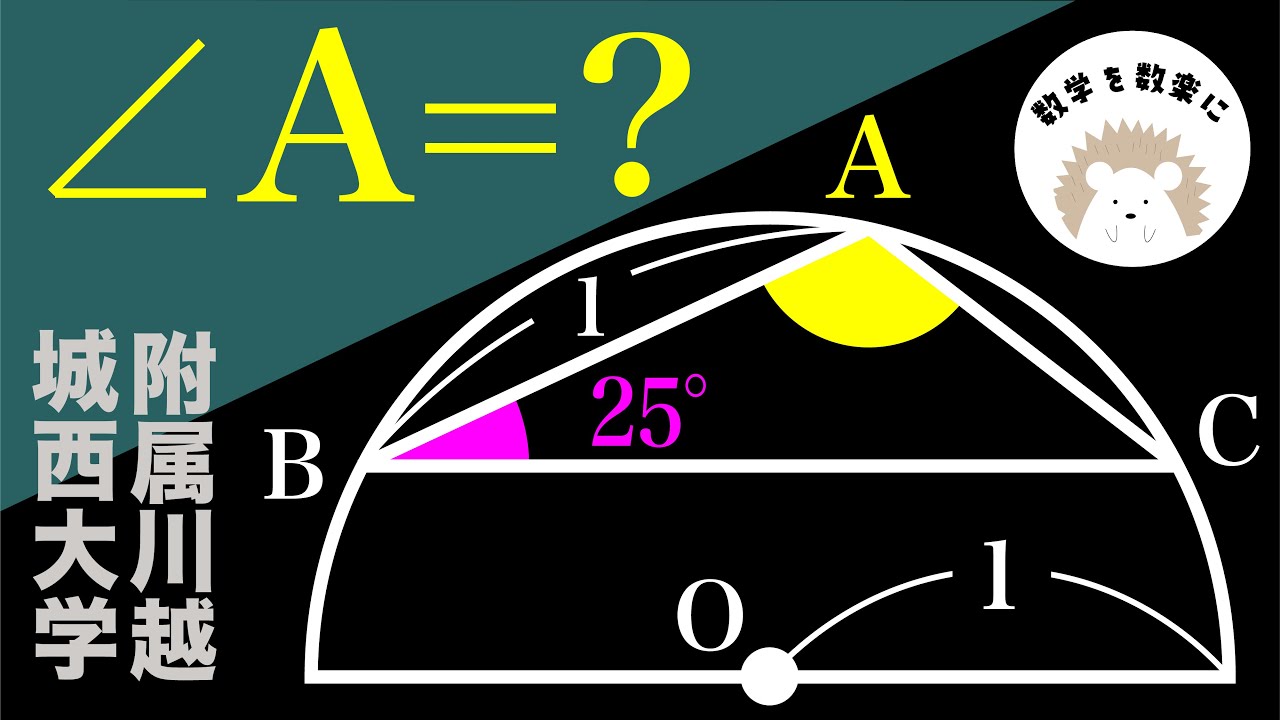
気がつけば一瞬でとろける。
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle A=?$
*図は動画内参照
城西大学付属川越高等学校
この動画を見る
$\angle A=?$
*図は動画内参照
城西大学付属川越高等学校
三角比この覚え方はどうでしょうか?

【高校数学】有名角の面白い覚え方~数学の先生は怒らないでね~【数学Ⅰ】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
有名角の面白い覚え方紹介動画です
この動画を見る
有名角の面白い覚え方紹介動画です
円の折り返し

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=?
*図は動画内参照
関西大倉高等学校
この動画を見る
斜線部の面積=?
*図は動画内参照
関西大倉高等学校
【数Ⅰ】有名角の値 三角比と方程式・不等式【覚えることを最小限に】

【数Ⅰ】三角比の相互関係【sinθからcosθを求める方法】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
三角比の相互関係sinθからcosθを求める方法に関して解説していきます.
この動画を見る
三角比の相互関係sinθからcosθを求める方法に関して解説していきます.
【数Ⅰ】三角比の導入から拡張まで【単位円ってどこから出てきたん?】

福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(1)〜楕円と複素数平面

単元:
#平面上の曲線#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#2次曲線#複素数平面#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
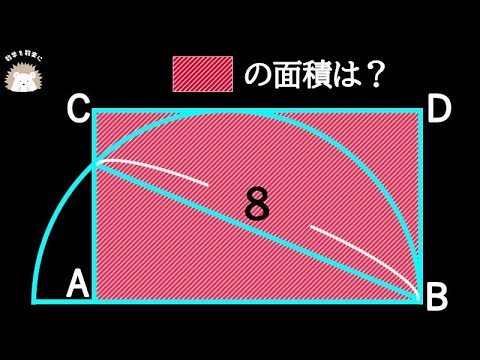
長方形と半円 3通りで解説しました
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
福田のわかった数学〜高校1年生058〜図形の計量(8)正四面体の外接球の半径

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(9)
1辺の長さがaである正四面体の各頂点を通る外接球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(9)
1辺の長さがaである正四面体の各頂点を通る外接球の半径を求めよ。
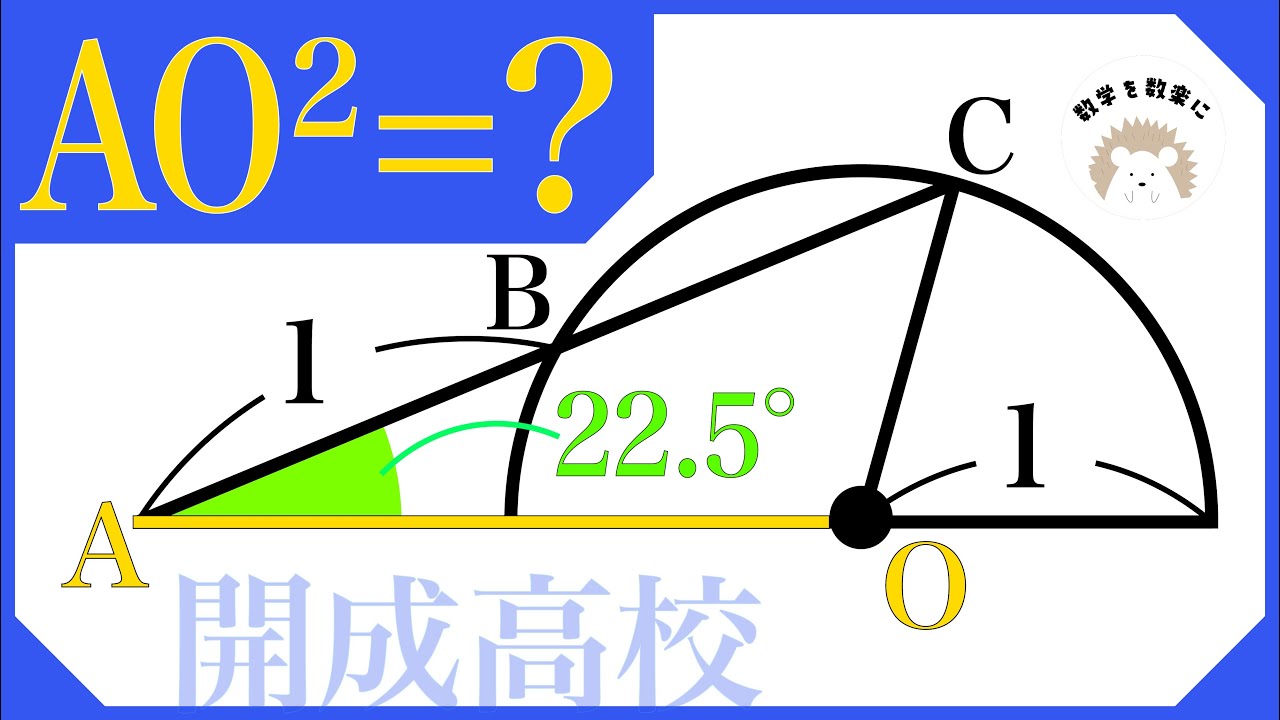
22.5°
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AO^2 =?$
*図は動画内参照
開成高等学校
この動画を見る
$AO^2 =?$
*図は動画内参照
開成高等学校
参りました。。。気付けば一瞬でした
福田のわかった数学〜高校1年生054〜図形の計量(5)四面体の体積(1)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(5)
四面体ABCDについて、
$AB=8,\ BC=4,\ CD=5,\ DA=8,\ BD=6,\ AC=8$
のとき体積を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(5)
四面体ABCDについて、
$AB=8,\ BC=4,\ CD=5,\ DA=8,\ BD=6,\ AC=8$
のとき体積を求めよ。
筑駒だけど気付けば一瞬!!

単元:
#算数(中学受験)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの三角形の面積の和=?
*図は動画内参照
筑波大学附属駒場中学校
この動画を見る
2つの三角形の面積の和=?
*図は動画内参照
筑波大学附属駒場中学校
福田のわかった数学〜高校1年生053〜図形の計量(4)三角形の成立条件と最大角

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(4)
三辺の長さが$x^2+x+1, -2x-1, x^2+2x$である三角形の最大角を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(4)
三辺の長さが$x^2+x+1, -2x-1, x^2+2x$である三角形の最大角を求めよ。
