 図形と計量
図形と計量
 図形と計量
図形と計量
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
tan7. 5°の華麗な求め方

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{eqnarray}
\frac{1}{\tan\frac{\pi}{24}}の値
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
\frac{1}{\tan\frac{\pi}{24}}の値
\end{eqnarray}
$
福田の数学〜中学生でも解ける大学入試問題〜明治大学2023年全学部統一ⅠⅡAB第1問(5)〜共通弦の長さ
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
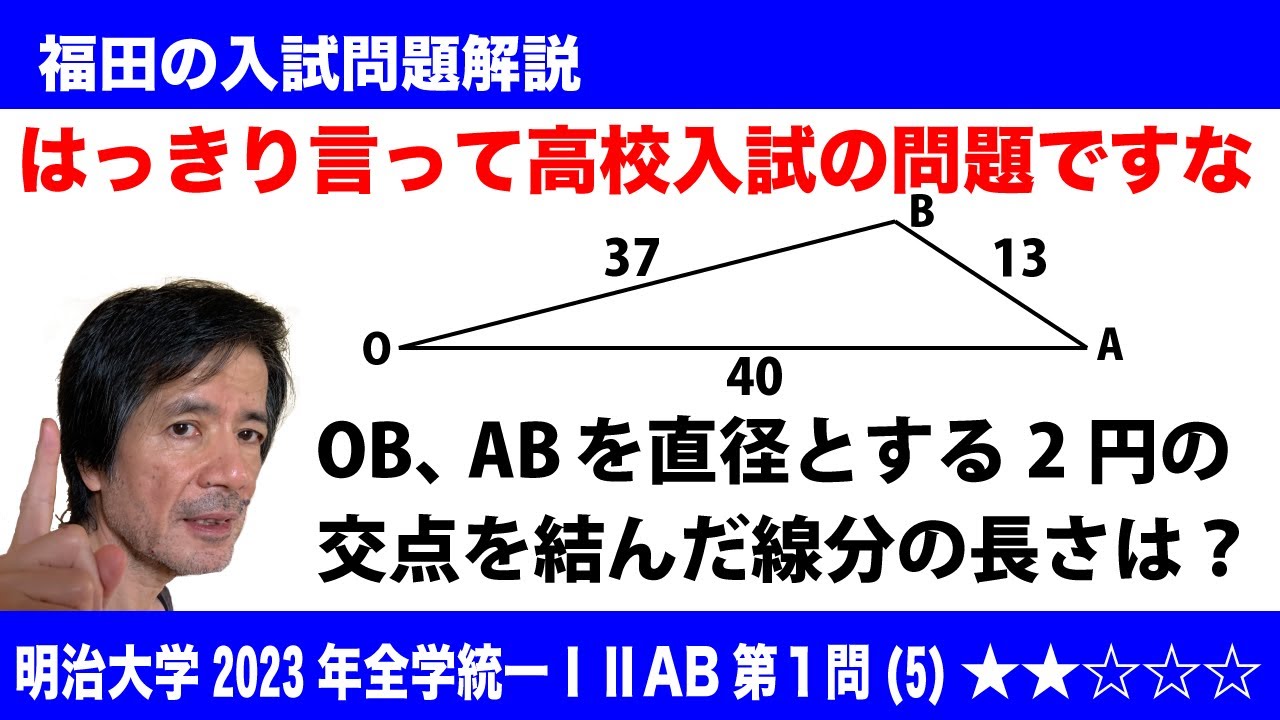
(5)原点をOとする座標平面上に点Aと点Bがある。点Aの座標は(40,0)であり、
点BはOB=37, AB=13 を満たす。この座標平面上でOBを直径とする円を$C_1$とし、ABを直径とする円を$C_2$とする。このとき、$C_1$と$C_2$の交点を結ぶ線分の長さは$\boxed{\ \ タチ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$
(5)原点をOとする座標平面上に点Aと点Bがある。点Aの座標は(40,0)であり、
点BはOB=37, AB=13 を満たす。この座標平面上でOBを直径とする円を$C_1$とし、ABを直径とする円を$C_2$とする。このとき、$C_1$と$C_2$の交点を結ぶ線分の長さは$\boxed{\ \ タチ\ \ }$である。
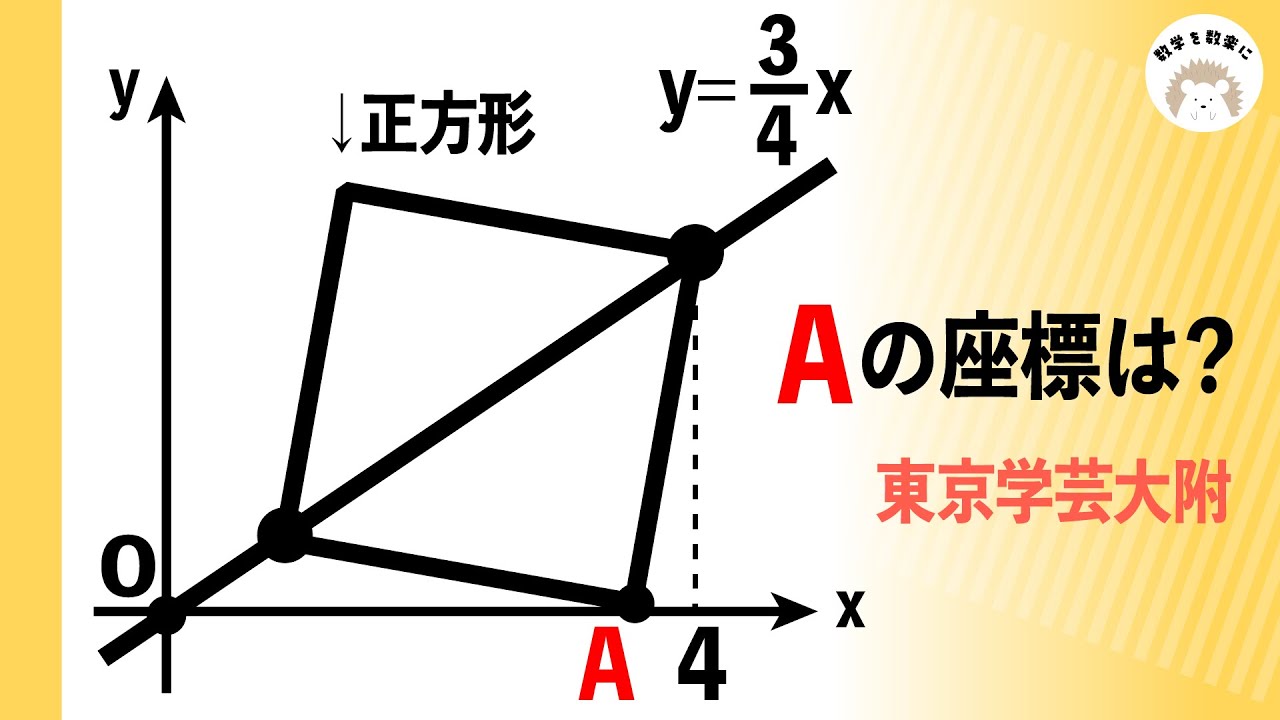
ここに補助線!! 関数だけど図形で解く!!東京学芸大学附属
【数Ⅰ】図形と計量:三角比への応用:3つのsinの比から角度を求める!

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,次の等式が成り立つとき,この三角形の最も大きい角の大きさを求めよ。
$\sin A:\sin B:\sin C=7:5:3$
この動画を見る
$△ABC$において,次の等式が成り立つとき,この三角形の最も大きい角の大きさを求めよ。
$\sin A:\sin B:\sin C=7:5:3$
【数Ⅰ】図形と計量:三角比への応用:「角の二等分線」の長さの求め方!
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
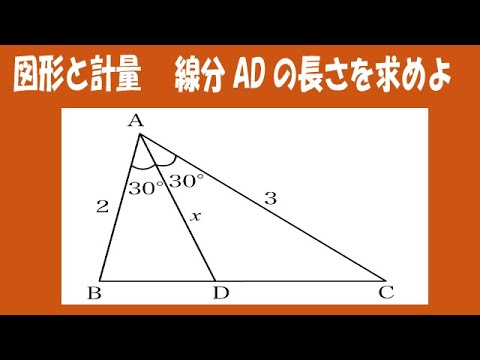
$△ABC$において,$AB=2,AC=3,A=60°$とし,$∠A$の二等分線と辺$BC$の交点を$D$とする。線分$AD$の長さを求めよ。
この動画を見る
$△ABC$において,$AB=2,AC=3,A=60°$とし,$∠A$の二等分線と辺$BC$の交点を$D$とする。線分$AD$の長さを求めよ。
こういう問題で差がつくのだ。円 高知県
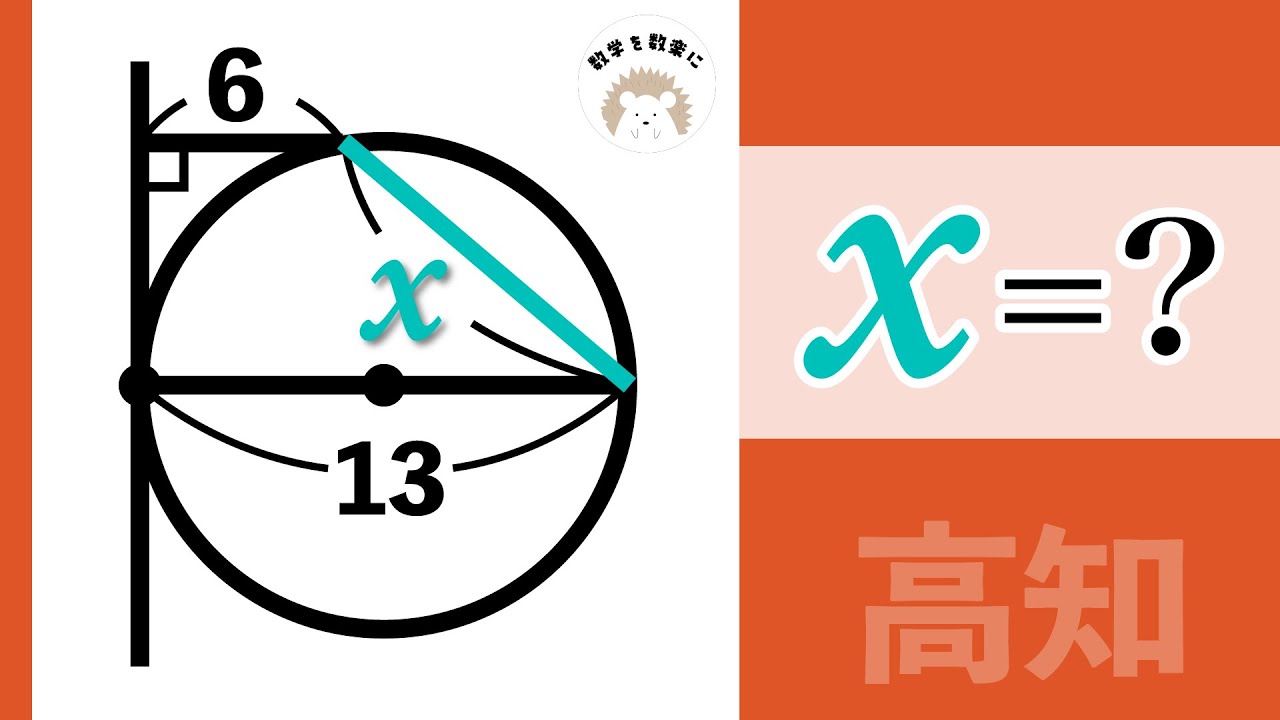
円周角の定理のなぜ?

福田の数学〜早稲田大学2023年商学部第1問(2)〜三角形の内接円の半径と不定方程式

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$m,n$は自然数。半径1の円に内接する$\triangle {ABC}$が
$\sin {\angle A}=\require{physics}\flatfrac{m}{17}$、$\sin {\angle B}=\require{physics}\flatfrac{n}{17}$、
$\sin^2\angle C=\sin^2\angle A+\sin^2\angle B$
を満たすとき、$\triangle {ABC}$の内接円の半径は?
2023早稲田大学商学部過去問
この動画を見る
$m,n$は自然数。半径1の円に内接する$\triangle {ABC}$が
$\sin {\angle A}=\require{physics}\flatfrac{m}{17}$、$\sin {\angle B}=\require{physics}\flatfrac{n}{17}$、
$\sin^2\angle C=\sin^2\angle A+\sin^2\angle B$
を満たすとき、$\triangle {ABC}$の内接円の半径は?
2023早稲田大学商学部過去問
有名問題
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
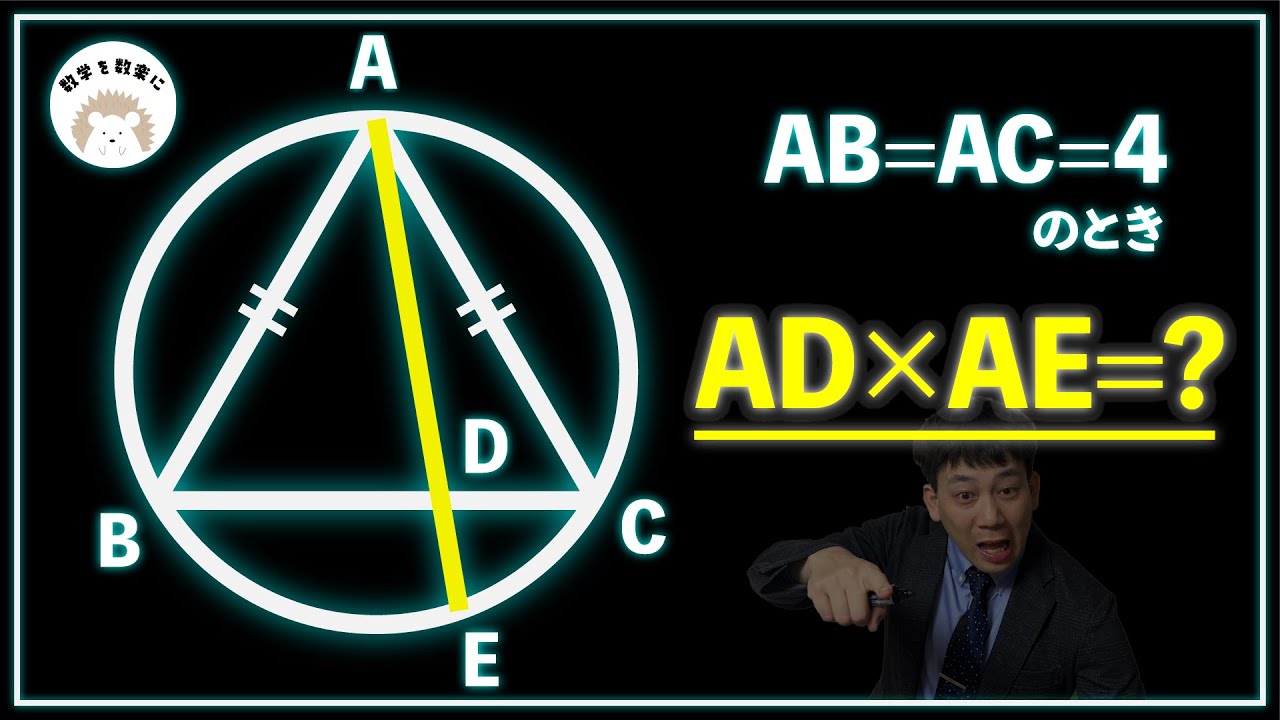
AB=AC=4のとき
AD×AE=?
*図は動画内参照
この動画を見る
AB=AC=4のとき
AD×AE=?
*図は動画内参照
【短時間でポイントチェック!!】内接円や外接円の三角形の面積〔現役講師解説、数学〕

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
※図は動画内参照
①Aは?
②CDは?
③四角形ABCDの面積は?
※図は動画内参照
①$\cos A$
②△ABCの面積$S$
③△ABCの内接円の半径$r$
この動画を見る
※図は動画内参照
①Aは?
②CDは?
③四角形ABCDの面積は?
※図は動画内参照
①$\cos A$
②△ABCの面積$S$
③△ABCの内接円の半径$r$
【短時間でポイントチェック!!】三角形の面積〔現役講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\sin$を使って求める三角形の面積
※図は動画内参照
①$\cos A$
②$\sin A$
③面積
この動画を見る
$\sin$を使って求める三角形の面積
※図は動画内参照
①$\cos A$
②$\sin A$
③面積
【テスト前に要点チェック!!】三角比まとめ(基礎・対称性・正弦定理・余弦定理)〔現役講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
三角比の基礎についてまとめました
基礎・対称性・正弦定理・余弦定理
この動画を見る
数学1A
三角比の基礎についてまとめました
基礎・対称性・正弦定理・余弦定理
気付けば一瞬!!tanθ=❓
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
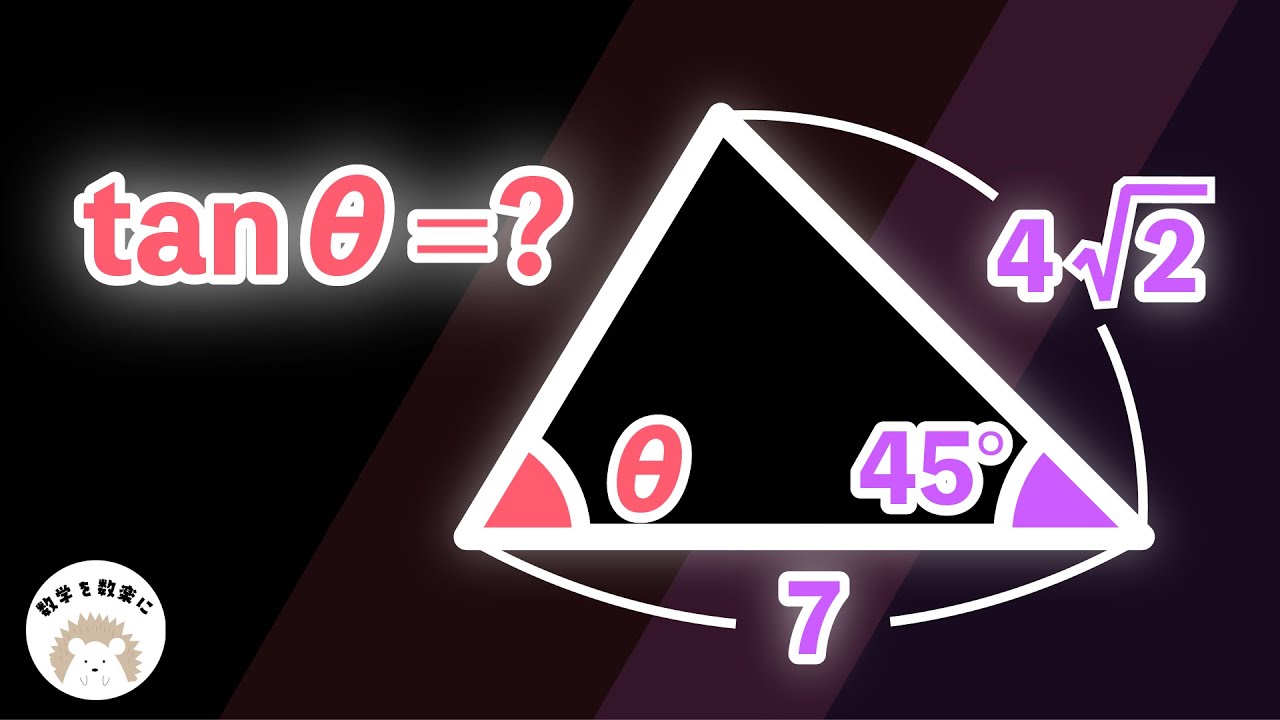
tanθ=?
*図は動画内参照
この動画を見る
tanθ=?
*図は動画内参照
【短時間でマスター!!】正弦定理・余弦定理を解説!〔現役講師解説、数学〕

面積比の利用 灘高校
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
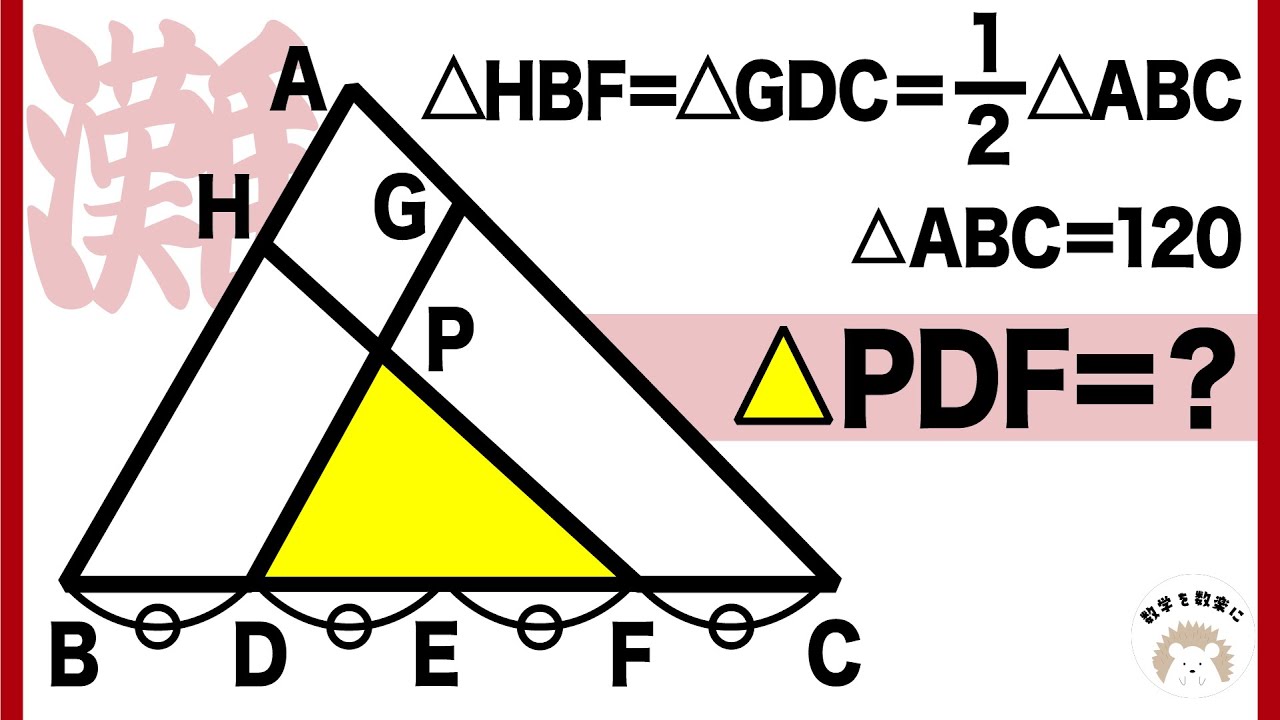
$△HBF=△GDC=\frac{1}{2}△ABC$
$△ABC=120$
$△PDF=?$
*図は動画内参照
この動画を見る
$△HBF=△GDC=\frac{1}{2}△ABC$
$△ABC=120$
$△PDF=?$
*図は動画内参照
解き方いろいろ 面積比 筑波大附属 訂正はコメント欄に
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
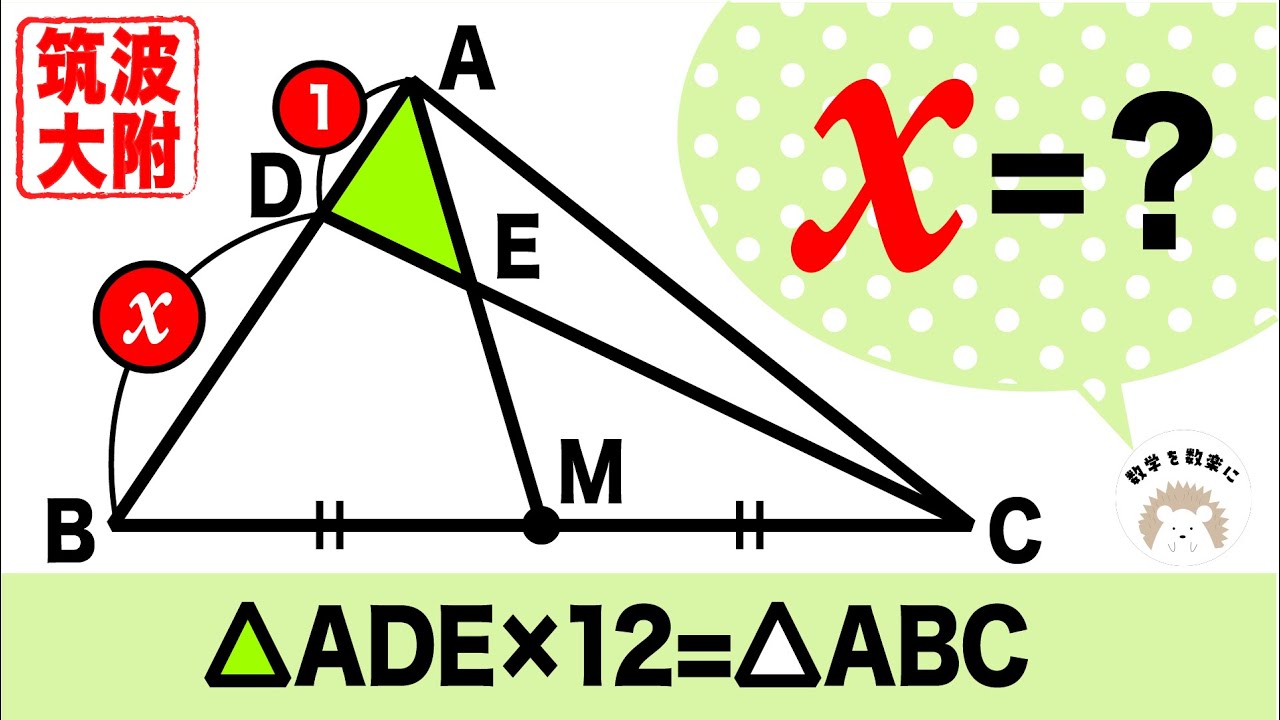
$△ADE×12=△ABC$
$x=?$
筑波大学付属高等学校
この動画を見る
$△ADE×12=△ABC$
$x=?$
筑波大学付属高等学校
【短時間でマスター!!】入試、模試や定期テストでとてもよく出る三角比の対称式を解説!(sin,cos,tanの求め方)〔現役講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
三角比の対称式
$0^{ \circ } \leqq \theta \leqq 180^{ \circ } ,\sin \theta + \cos \theta = \frac {2}{3}$
①$\sin \theta \cos \theta$
②$\sin^3 \theta + \cos^3 \theta$
この動画を見る
数学1A
三角比の対称式
$0^{ \circ } \leqq \theta \leqq 180^{ \circ } ,\sin \theta + \cos \theta = \frac {2}{3}$
①$\sin \theta \cos \theta$
②$\sin^3 \theta + \cos^3 \theta$
なかなかの難問 江戸川学園取手

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
3辺の長さが$a , 2a , a^2$の直角三角形がある。
この三角形の面積を求めよ。
(1 < a < 2)
江戸川学園取手高等学校
この動画を見る
3辺の長さが$a , 2a , a^2$の直角三角形がある。
この三角形の面積を求めよ。
(1 < a < 2)
江戸川学園取手高等学校
【短時間でマスター!!】90°-θの三角比を解説!(sin,cos,tanの求め方)〔現役講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
$90^{ \circ } - \theta $の三角比
$45^{ \circ } $以下の三角比で表せ。
①$\sin 67^{ \circ }$
②$\cos 89^{ \circ }$
③$\tan 50^{ \circ }$
この動画を見る
数学1A
$90^{ \circ } - \theta $の三角比
$45^{ \circ } $以下の三角比で表せ。
①$\sin 67^{ \circ }$
②$\cos 89^{ \circ }$
③$\tan 50^{ \circ }$
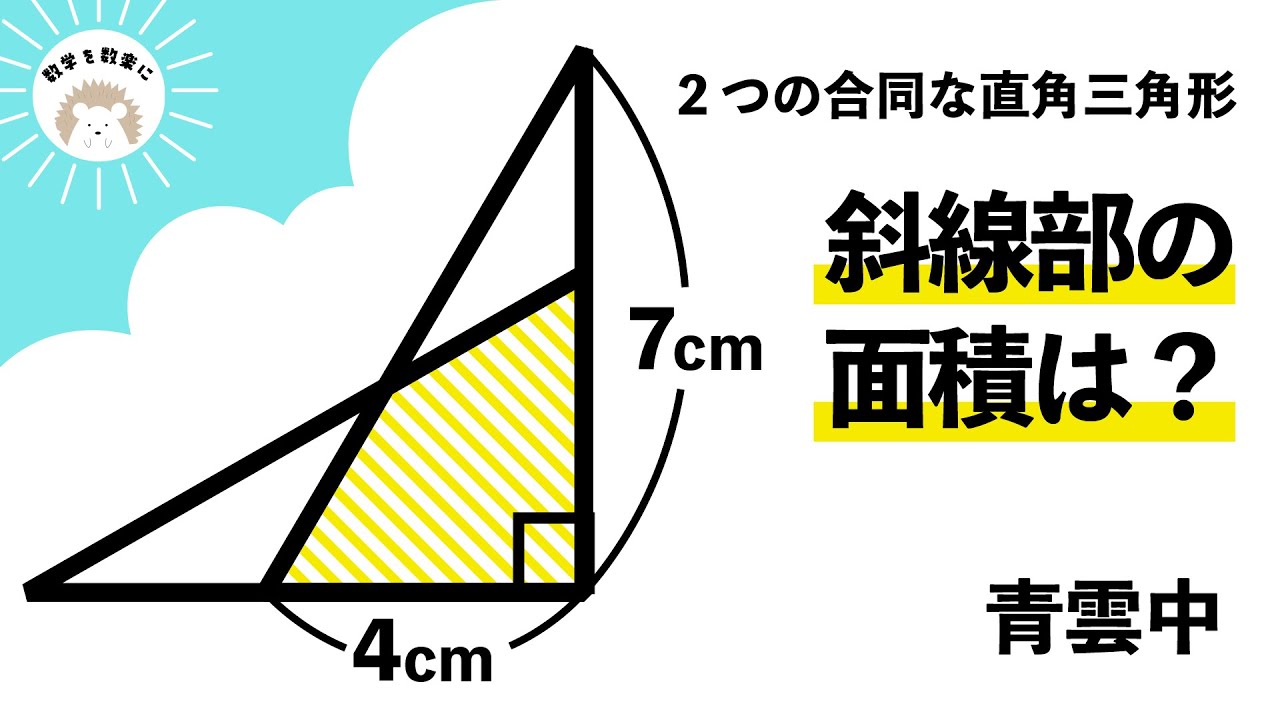
2つの合同な直角三角形 斜線部の面積=❓ 青雲中
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△BDA $\equiv$ △CFA
四角形EFDAの面積は?
*図は動画内参照
青雲中学校
この動画を見る
△BDA $\equiv$ △CFA
四角形EFDAの面積は?
*図は動画内参照
青雲中学校
【短時間でマスター!!】三角比の相互関係を解説!(sin,cos,tanの求め方)〔現役講師解説、数学〕

単元:
#中3数学#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
三角比の相互関係を解説します。
$\sin,\cos,\tan$の求め方
$0^{\circ}\leqq\theta\leqq180^{\circ}$
$\sin\theta=\frac{1}{3}$のとき$\cos\theta,\tan\theta$は?
この動画を見る
数学1A
三角比の相互関係を解説します。
$\sin,\cos,\tan$の求め方
$0^{\circ}\leqq\theta\leqq180^{\circ}$
$\sin\theta=\frac{1}{3}$のとき$\cos\theta,\tan\theta$は?
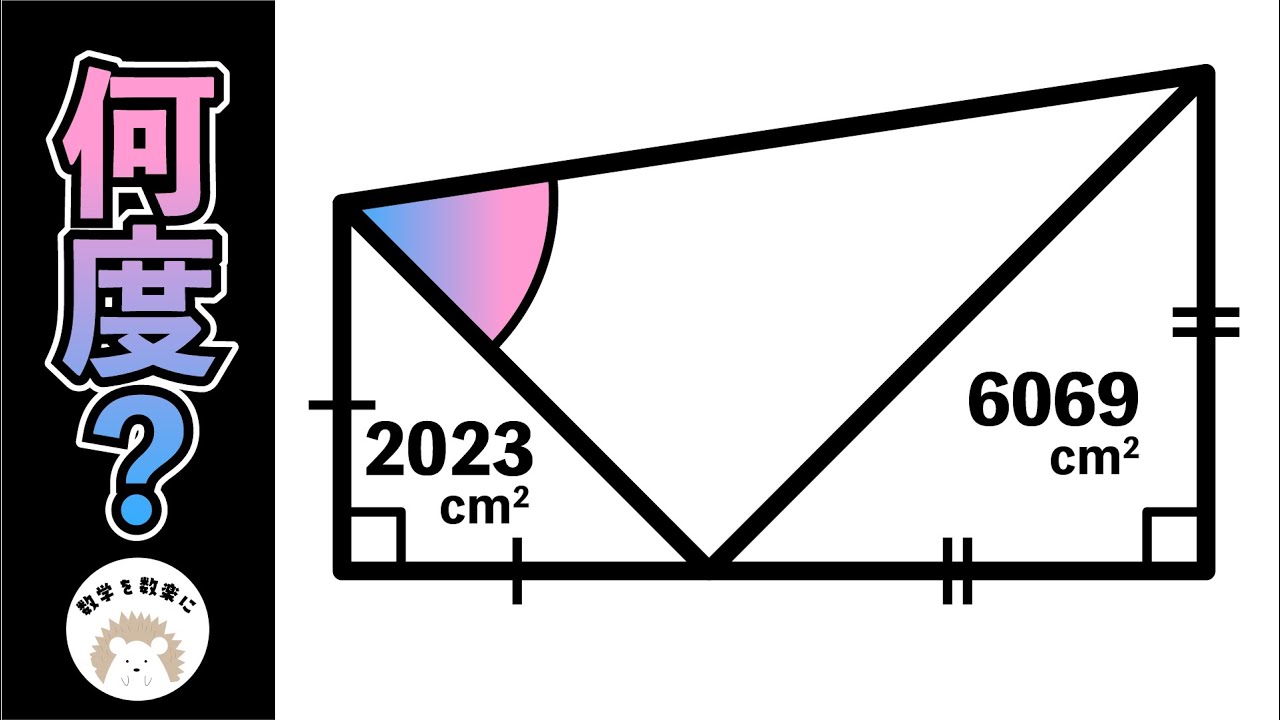
面積と角度
【短時間でマスター!!】三角比を解説!(sin,cos,tanの求め方)〔現役講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
三角比の基礎について解説します。
この動画を見る
数学1A
三角比の基礎について解説します。
sinとcosの関係

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
sinとcosの関係
*図は動画内参照
この動画を見る
sinとcosの関係
*図は動画内参照
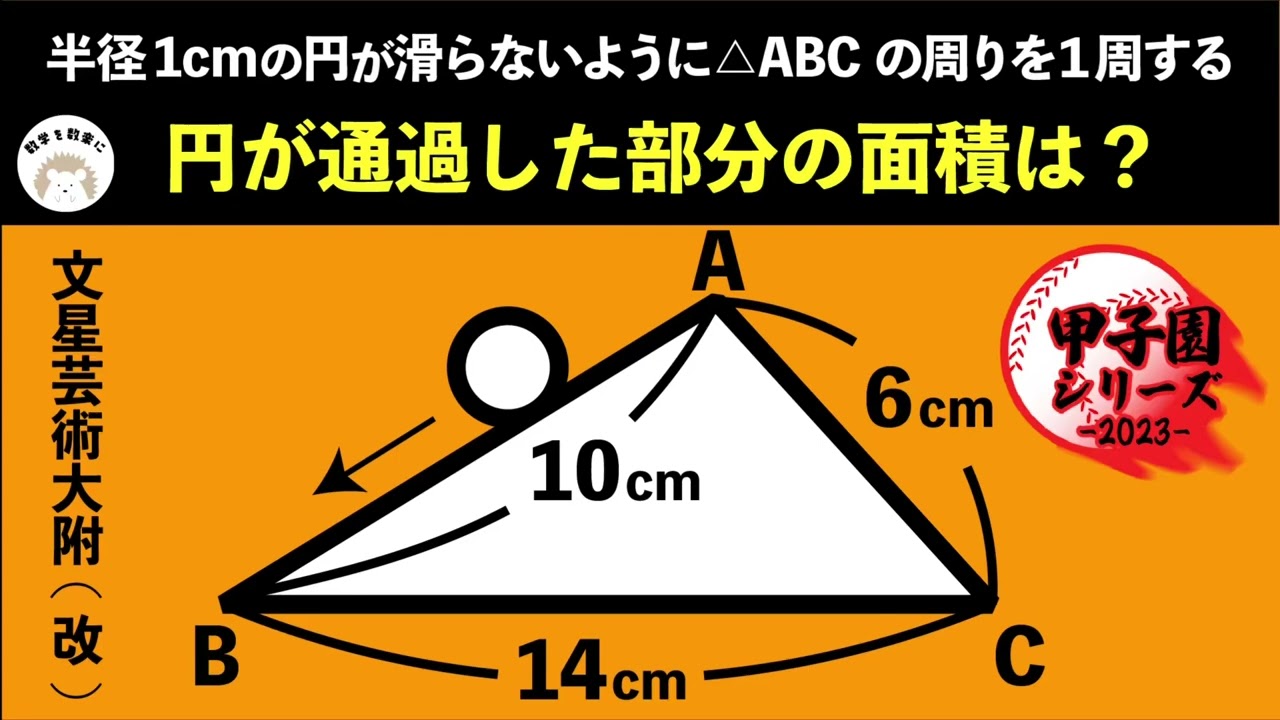
円が通過した面積は?文星芸術大附属(栃木県)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径1cmの円が滑らないように△ABCの周りを1周する
円が通過した部分の面積は?
*図は動画内参照
文星芸術大学附属高等学校(改)
この動画を見る
半径1cmの円が滑らないように△ABCの周りを1周する
円が通過した部分の面積は?
*図は動画内参照
文星芸術大学附属高等学校(改)
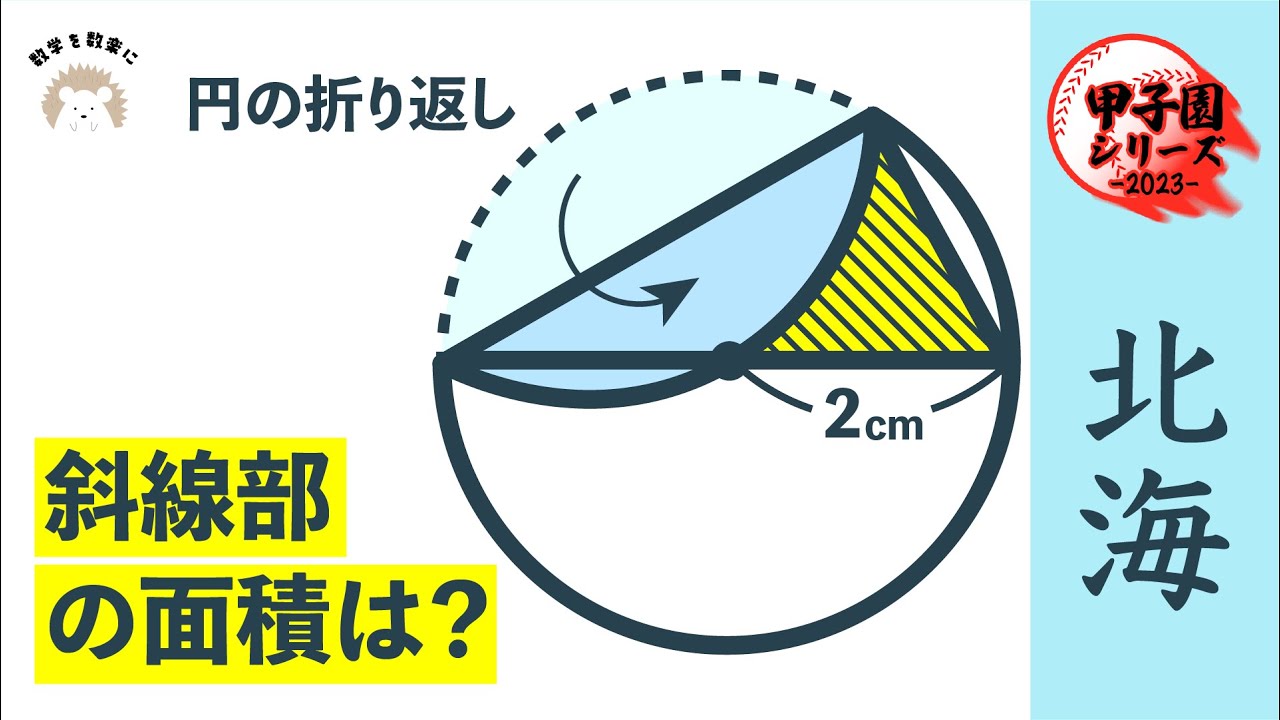
円の折り返し 北海 (南北海道)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の折り返し
斜線部の面積は?
*図は動画内参照
(南北海道)
この動画を見る
円の折り返し
斜線部の面積は?
*図は動画内参照
(南北海道)
円周角 2通りで解説 智辯学園 (奈良)
サラッと解説してますが、実際解くときは結構試行錯誤してます。円と角の二等分 土浦日大(茨城県)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
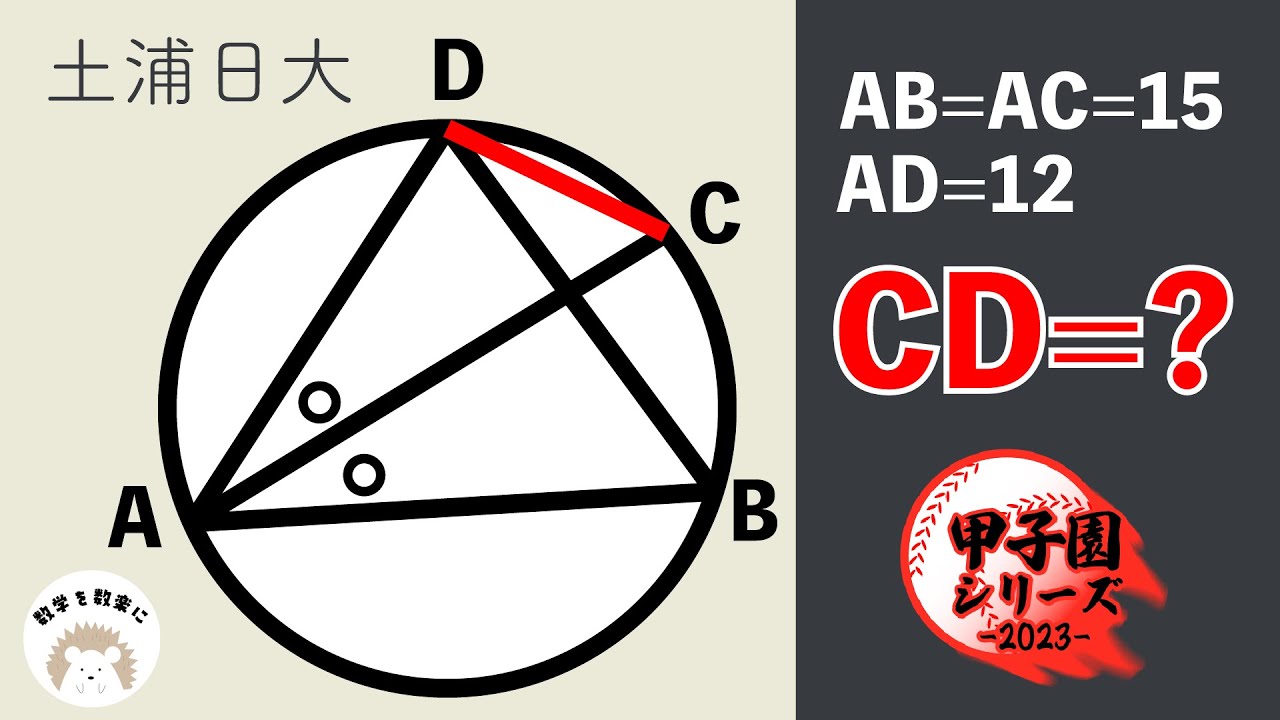
$AB=AC=15$
$AD=12$
$CD=?$
*図は動画内参照
土浦日本大学高等学校
この動画を見る
$AB=AC=15$
$AD=12$
$CD=?$
*図は動画内参照
土浦日本大学高等学校
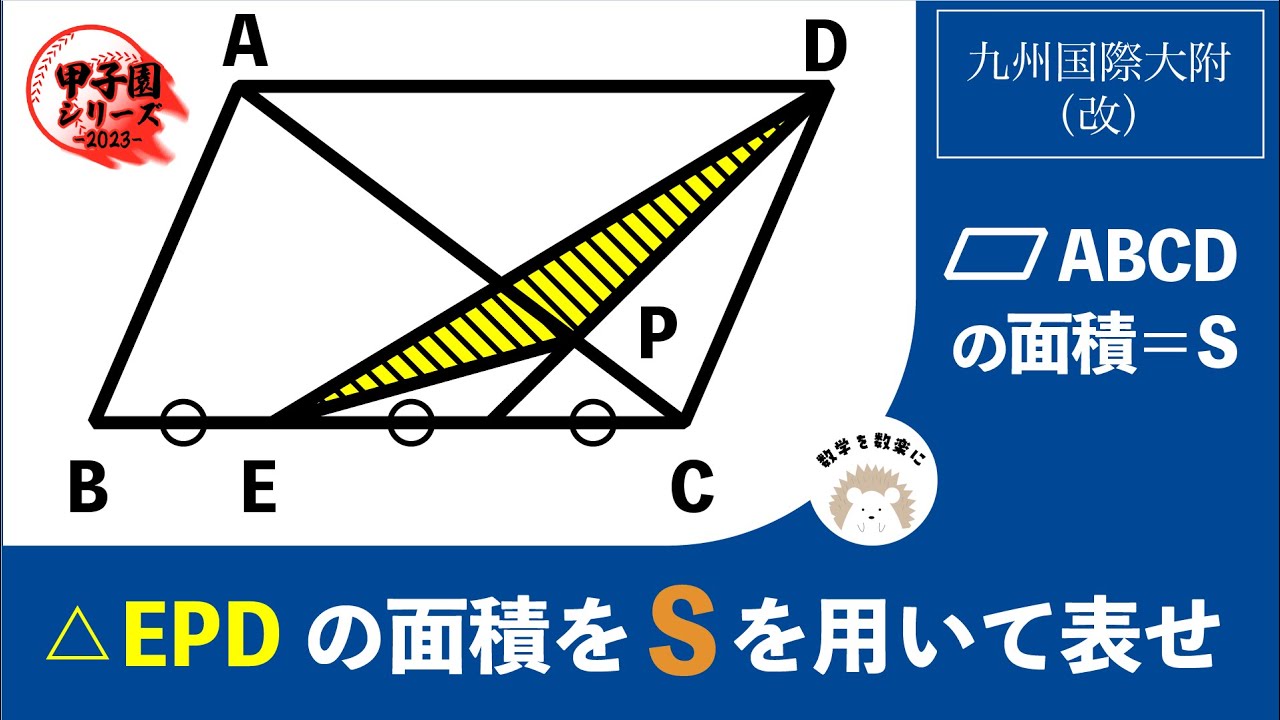
面積比 九州国際大附属 (福岡県)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
▱ABCDの面積=S
△EPDの面積をSを用いて表せ
*図は動画内参照
九州国際大学付属高等学校(改)
この動画を見る
▱ABCDの面積=S
△EPDの面積をSを用いて表せ
*図は動画内参照
九州国際大学付属高等学校(改)
