 図形と計量
図形と計量
 図形と計量
図形と計量
図形と計量 円に内接する四角形の面積【烈's study!がていねいに解説】
単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
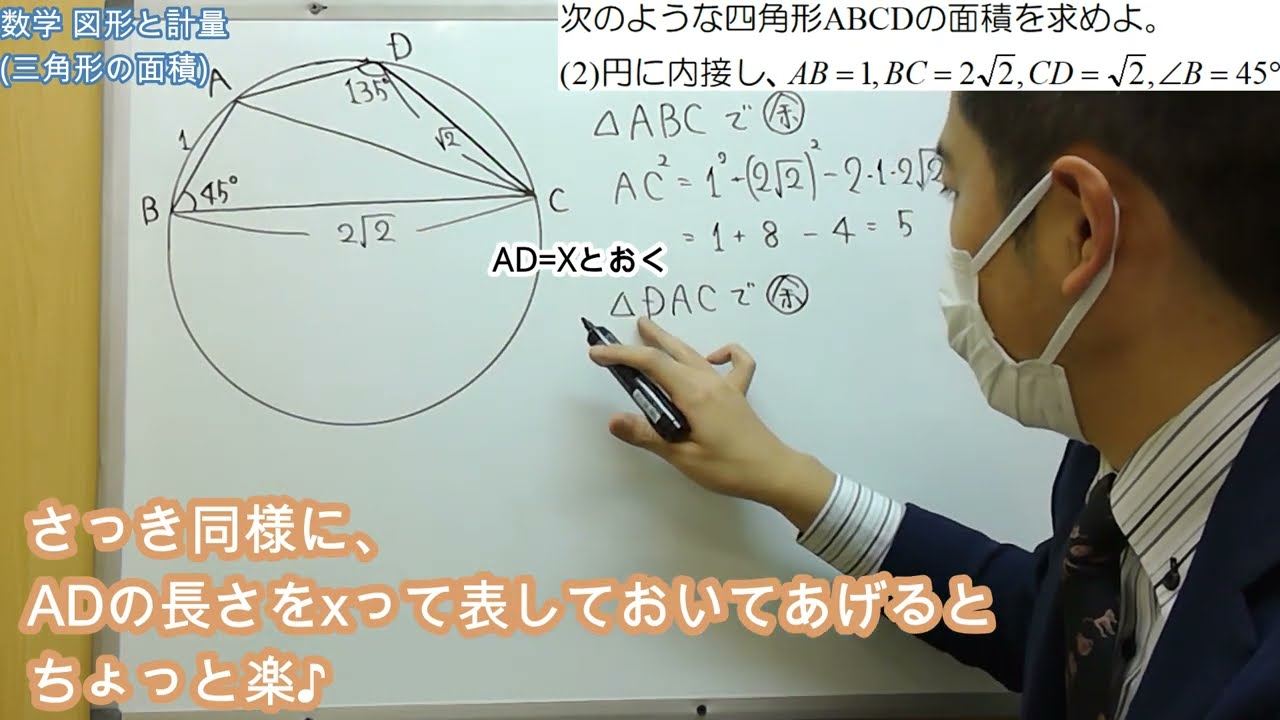
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
図形と計量 四角形の面積【烈's study!がていねいに解説】

単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
中学数学で三角比の相互関係を導く~あーずかいに数学教えてみた~

図形と計量 三角形の面積 二等分線の利用【烈's study!がていねいに解説】
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
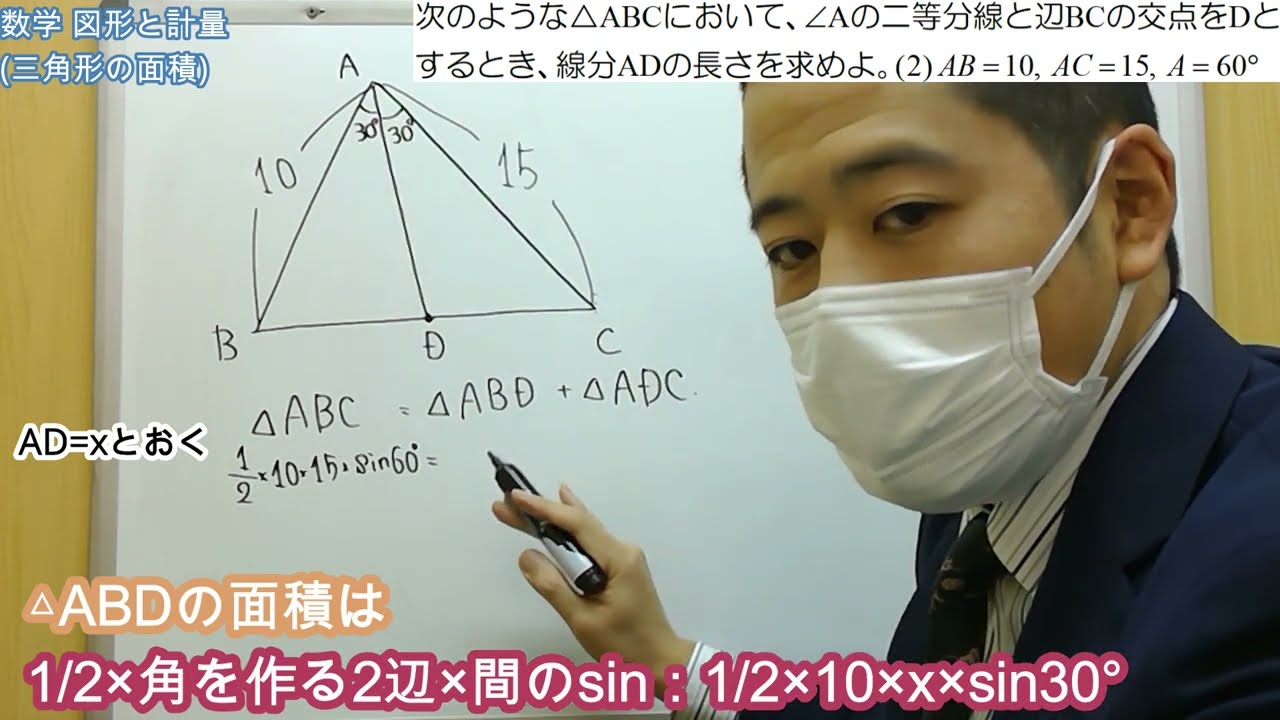
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
この動画を見る
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
図形と計量 平行四辺形の面積を求める【烈's study!がていねいに解説】

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような平行四辺形ABCDの面積を求めよ。
(1)$AB=3、BC=5、\angle ABC=60°$
(2)$AB=4、AD=6、\angle ABC=135°$
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)$AB=3、BC=5、\angle ABC=60°$
(2)$AB=4、AD=6、\angle ABC=135°$
図形と計量 正弦定理と余弦定理の応用、図形を利用して有名角以外を求める【烈's study!がていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
図を利用して、$\sin105°$と$\cos105°$の値を求めよ。
この動画を見る
図を利用して、$\sin105°$と$\cos105°$の値を求めよ。
図形と計量 正弦定理と余弦定理の応用、測量の考え方【烈's study!がていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、$AB=400m、BC=100\sqrt3 m,\angle QAB=30°,\angle PBA=\angle QBC=75°,\angle PCB=45°$であった。P、Q間の距離を求めよ。
この動画を見る
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、$AB=400m、BC=100\sqrt3 m,\angle QAB=30°,\angle PBA=\angle QBC=75°,\angle PCB=45°$であった。P、Q間の距離を求めよ。
福田の数学〜慶應義塾大学2023年薬学部第1問(4)〜球面上の3点が作る三角形

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#円と方程式#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)座標空間に球面S:$(x-3)^2$+$(y+2)^2$+$(z-1)^2$=36 がある。球面Sが平面y=2 と交わってできる円をCとおく。
(i)円Cの中心の座標は$\boxed{\ \ ク\ \ }$であり、半径は$\boxed{\ \ ケ\ \ }$である。
(ii)円Cと平面x=3の交点をA,Bとし、AとB以外の球面S上の任意の点をPとする。三角形PABにおいて、辺PBを4:3に内分する点をD、線分ADを5:3に内分する点をMとし、直線PMと辺ABとの交点をEとする。このとき、AEの長さは$\boxed{\ \ コ\ \ }$である。ただし、Bのz座標はAのz座標よりも大きいとする。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (4)座標空間に球面S:$(x-3)^2$+$(y+2)^2$+$(z-1)^2$=36 がある。球面Sが平面y=2 と交わってできる円をCとおく。
(i)円Cの中心の座標は$\boxed{\ \ ク\ \ }$であり、半径は$\boxed{\ \ ケ\ \ }$である。
(ii)円Cと平面x=3の交点をA,Bとし、AとB以外の球面S上の任意の点をPとする。三角形PABにおいて、辺PBを4:3に内分する点をD、線分ADを5:3に内分する点をMとし、直線PMと辺ABとの交点をEとする。このとき、AEの長さは$\boxed{\ \ コ\ \ }$である。ただし、Bのz座標はAのz座標よりも大きいとする。
2023慶應義塾大学薬学部過去問
図形問題にみえて実は〇〇問題 慶應義塾高校

単元:
#数Ⅰ#数A#図形と計量#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
nは3以上の整数とする。
正n角形の1つの内角をx°とするときxの値が整数となる正n角形は何個?
慶應義塾高等学校
この動画を見る
nは3以上の整数とする。
正n角形の1つの内角をx°とするときxの値が整数となる正n角形は何個?
慶應義塾高等学校
福田の数学〜京都大学2023年文系第3問〜半径1の円に内接する正五角形の一辺の長さの計量

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$(1)$\cos 2\theta$と$\cos 3\theta$を$\cos\theta$の式として表せ。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいな否かを理由をつけて判定せよ。
2023京都大学文系過去問
この動画を見る
$\Large\boxed{3}$(1)$\cos 2\theta$と$\cos 3\theta$を$\cos\theta$の式として表せ。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいな否かを理由をつけて判定せよ。
2023京都大学文系過去問
都立西 図形の証明 積が等しい 2023
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
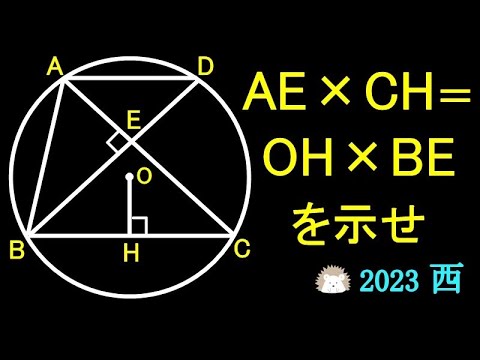
$AE \times CH = OH \times BE$を示せ
*図は動画内参照
2023西高等学校
この動画を見る
$AE \times CH = OH \times BE$を示せ
*図は動画内参照
2023西高等学校
福田の数学〜東京大学2023年文系第4問〜四面体の体積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
豪華すぎる生徒達 面積=❓
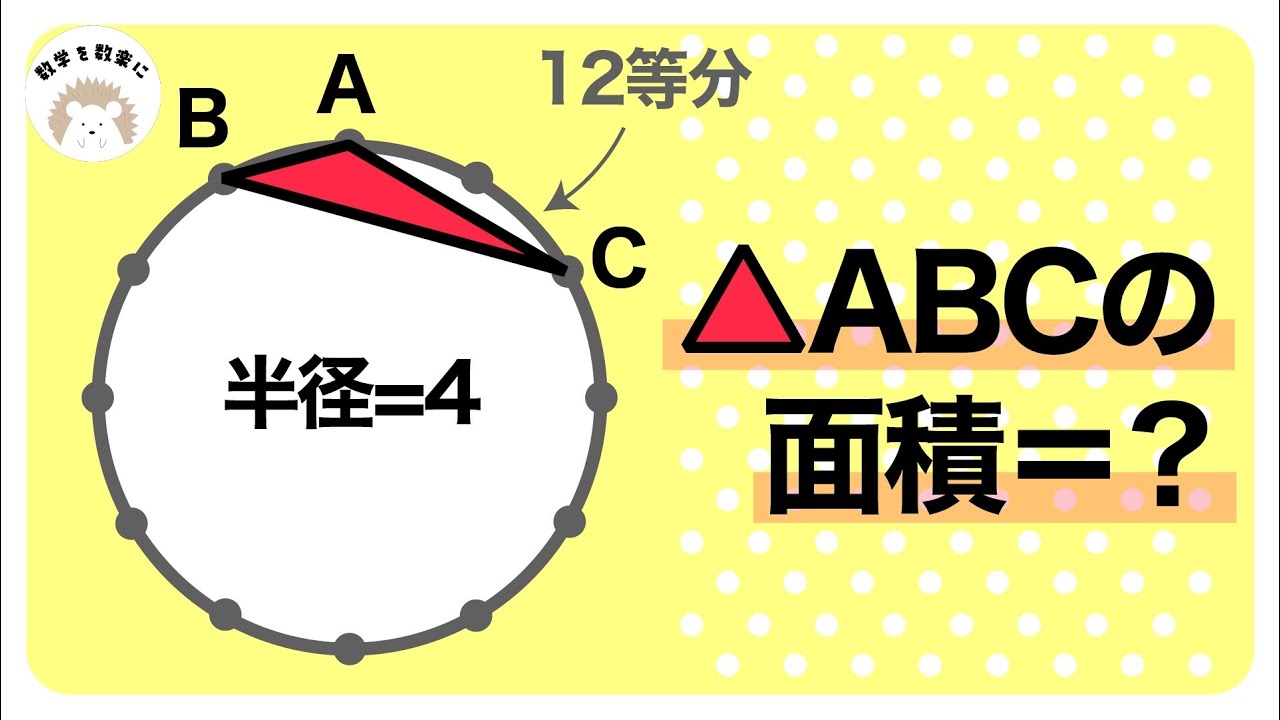
誰も解けなかった入試問題 2023高校入試数学解説70問目 円の難問 千葉県
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
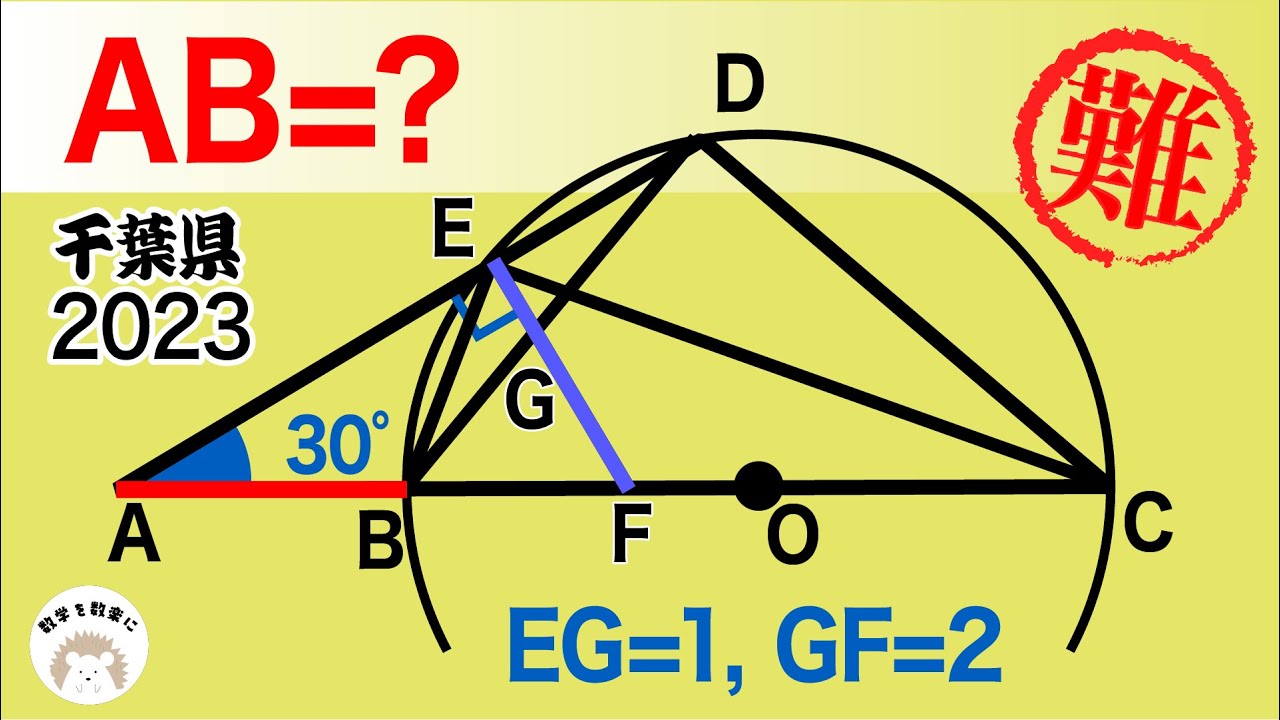
EG=1,GF=2
AB=?
*図は動画内参照
2023千葉県
この動画を見る
EG=1,GF=2
AB=?
*図は動画内参照
2023千葉県
福田の1.5倍速演習〜合格する重要問題084〜東北大学2018年度理系第4問〜三角形の内接円と外接円の半径の関係

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#三角比(三角比・拡張・相互関係・単位円)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 三角形ABCの内接円の半径をr, 外接円の半径をRとし、h=$\frac{r}{R}$とする。
また、$\angle$A=2α, $\angle$B=2β, $\angle$C=2γ とおく。
(1)h=4$\sin\alpha\sin\beta\sin\gamma$となることを示せ。
(2)三角形ABCが直角三角形のときh≦$\sqrt 2-1$が成り立つことを示せ。
また、等号が成り立つのはどのような場合か。
(3)一般の三角形ABCに対してh≦$\frac{1}{2}$が成り立つことを示せ。また等号が成り立つのはどのような場合か。
2018東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 三角形ABCの内接円の半径をr, 外接円の半径をRとし、h=$\frac{r}{R}$とする。
また、$\angle$A=2α, $\angle$B=2β, $\angle$C=2γ とおく。
(1)h=4$\sin\alpha\sin\beta\sin\gamma$となることを示せ。
(2)三角形ABCが直角三角形のときh≦$\sqrt 2-1$が成り立つことを示せ。
また、等号が成り立つのはどのような場合か。
(3)一般の三角形ABCに対してh≦$\frac{1}{2}$が成り立つことを示せ。また等号が成り立つのはどのような場合か。
2018東北大学理系過去問
2023高校入試数学解説57問目 群馬県前期ラストの問題
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
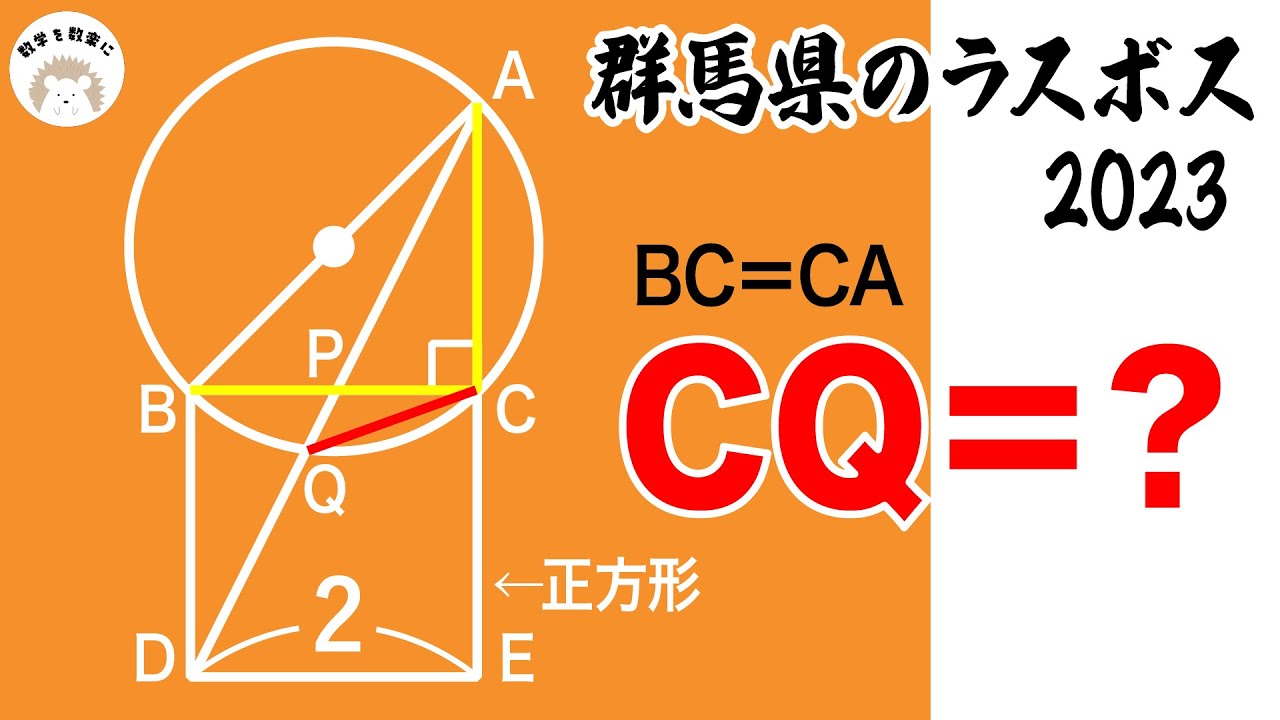
BC=CA
(1)$\angle AQC = ?$
(2)$△ABP∽△CQP$を示せ
(3)CQ=?
*図は動画内参照
2023群馬県 最後の問題
この動画を見る
BC=CA
(1)$\angle AQC = ?$
(2)$△ABP∽△CQP$を示せ
(3)CQ=?
*図は動画内参照
2023群馬県 最後の問題
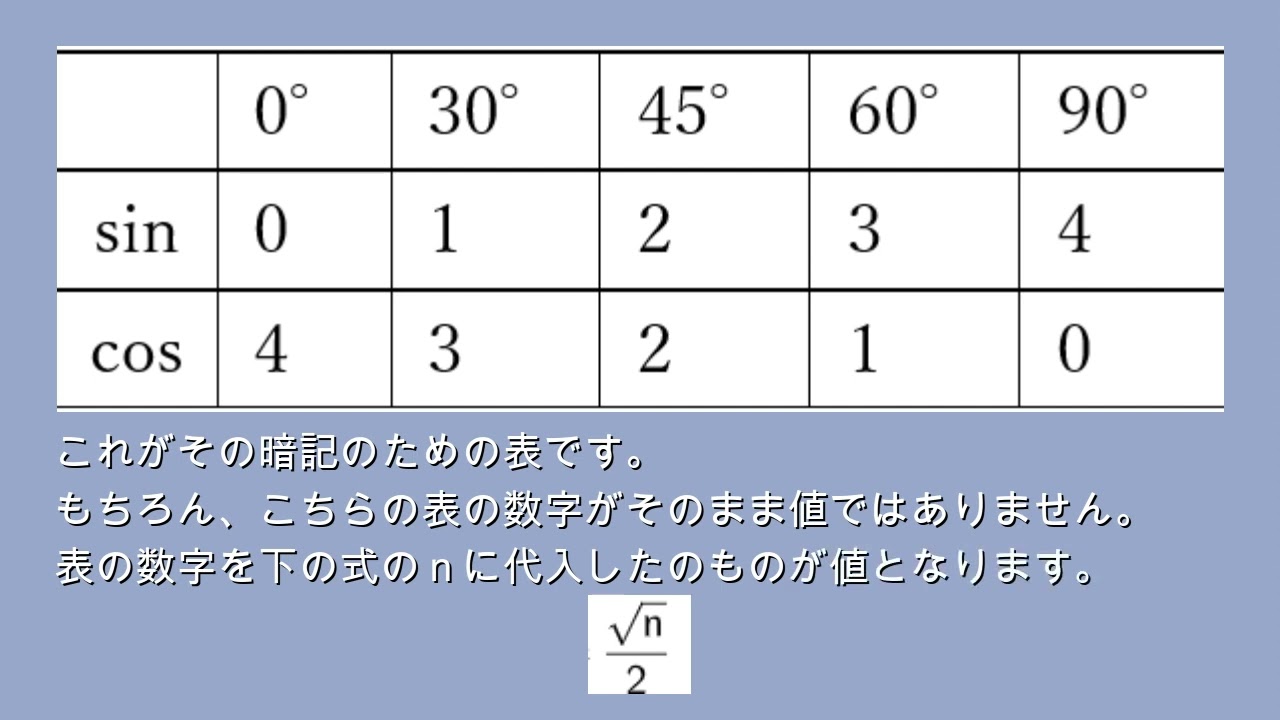
【数Ⅰ】文系にオススメ!三角比暗記法
2023高校入試数学解説50問目 手強い面積比 神奈川県 別解求む
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
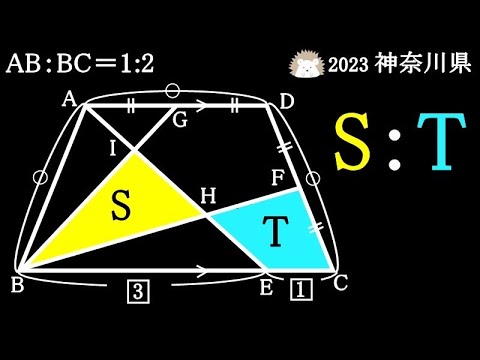
AB:BC=1:2
△IBH:四角形HECF=?
*図は動画内参照
2023神奈川県
この動画を見る
AB:BC=1:2
△IBH:四角形HECF=?
*図は動画内参照
2023神奈川県
2023高校入試数学解説48問目 見えないものを見ようとして桐朋

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
A,F,E,Dは同一円周上にあることを示せ
*図は動画内参照
2023 桐朋高等学校
この動画を見る
A,F,E,Dは同一円周上にあることを示せ
*図は動画内参照
2023 桐朋高等学校
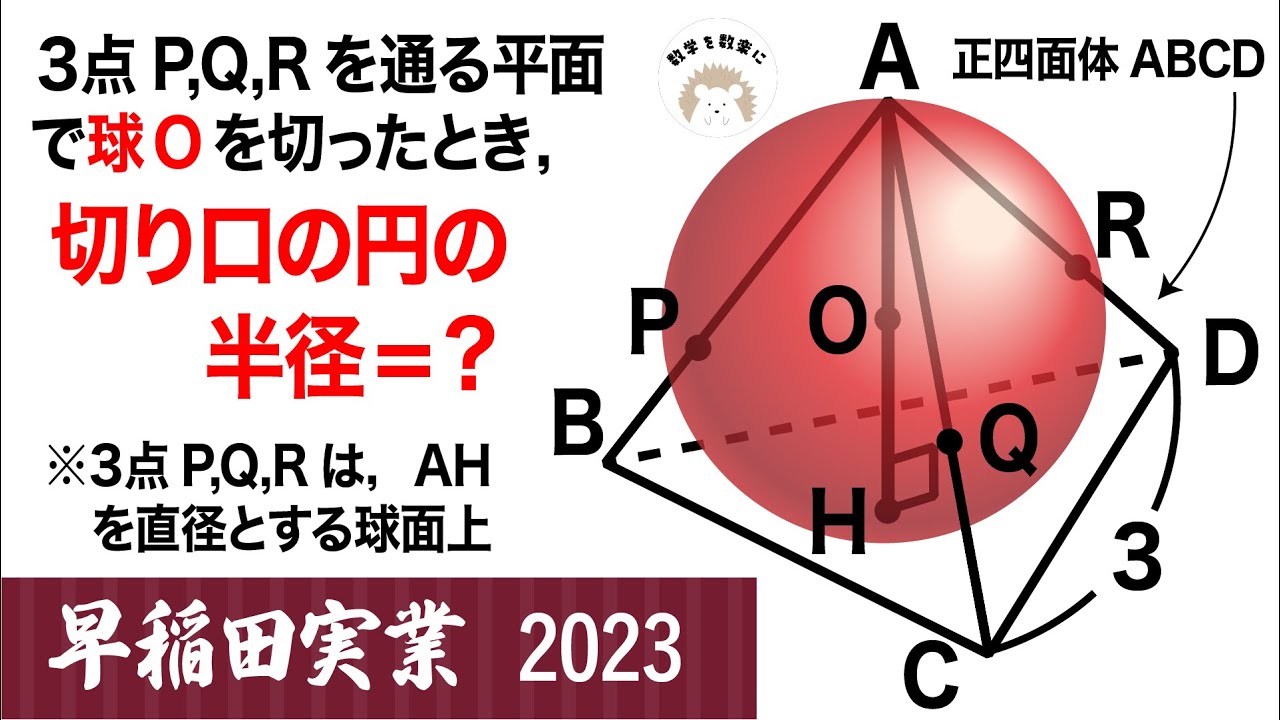
2023高校入試解説40問目 球の切り口 早稲田実業(改)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3点P,Q,Rを通る平面で球Oを切ったとき、切り口の円の半径=?
*3点P,Q,Rは、AHを直径とする球面上
*図は動画内参照
2023早稲田実業学校
この動画を見る
3点P,Q,Rを通る平面で球Oを切ったとき、切り口の円の半径=?
*3点P,Q,Rは、AHを直径とする球面上
*図は動画内参照
2023早稲田実業学校
2023高校入試解説32問目 3辺の長さがわかれば面積求まる 桃山学院

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
2023桃山学院高等学校
この動画を見る
△ABC=?
*図は動画内参照
2023桃山学院高等学校
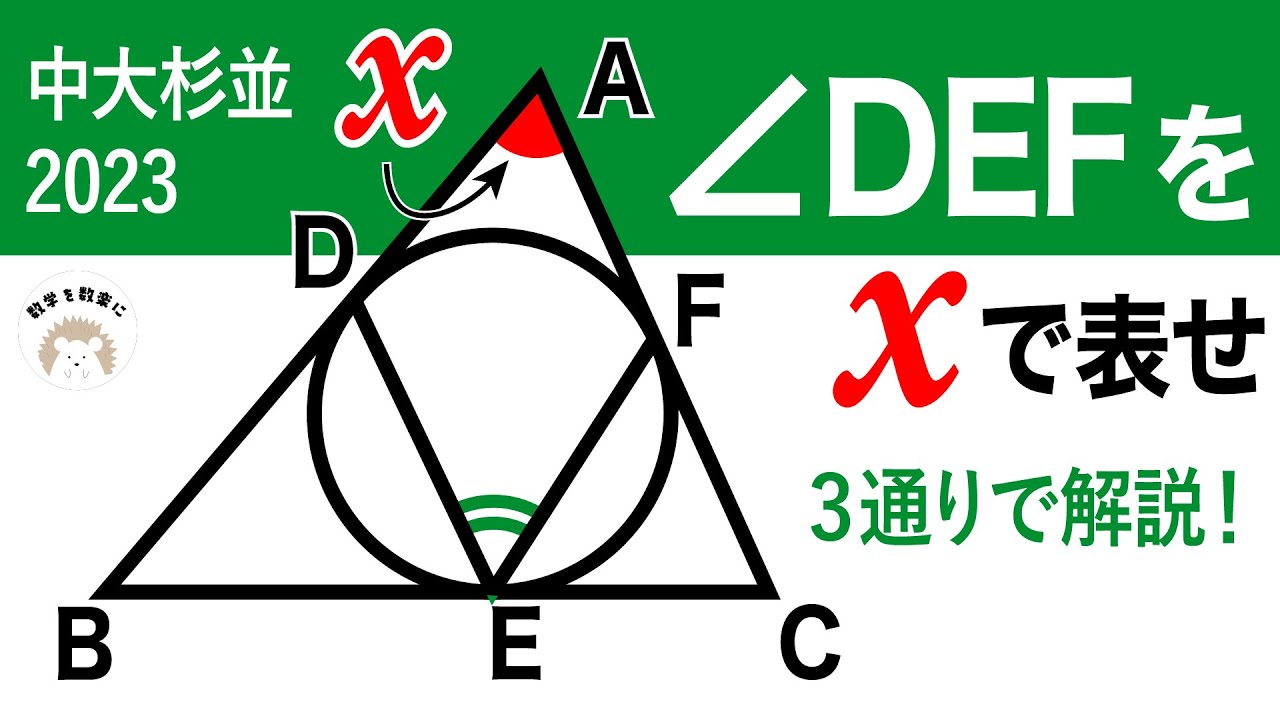
2023高校入試解説35問目 円と角度 中大杉並
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle DEF$をxで表せ
*図は動画内参照
2023中央大学杉並高等学校
この動画を見る
$\angle DEF$をxで表せ
*図は動画内参照
2023中央大学杉並高等学校
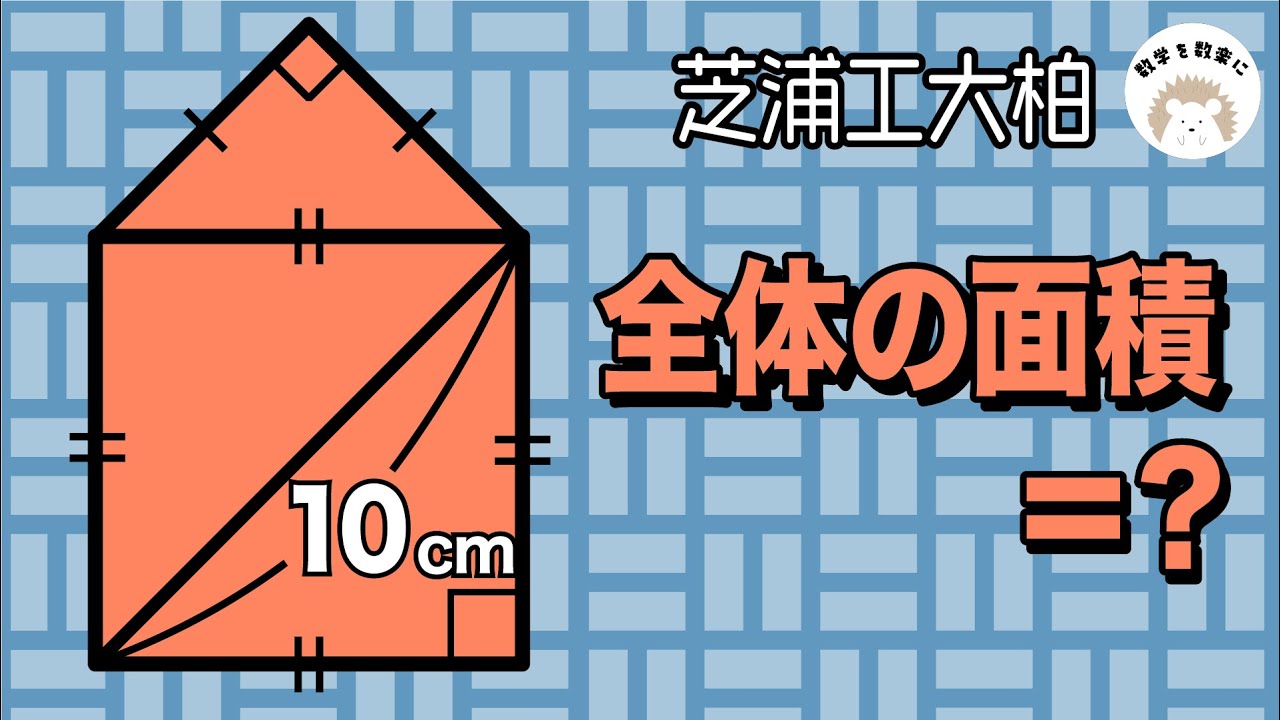
全体の面積を求めよ

五角形の面積=❓ 芝浦工大柏 〇〇先生登場!!
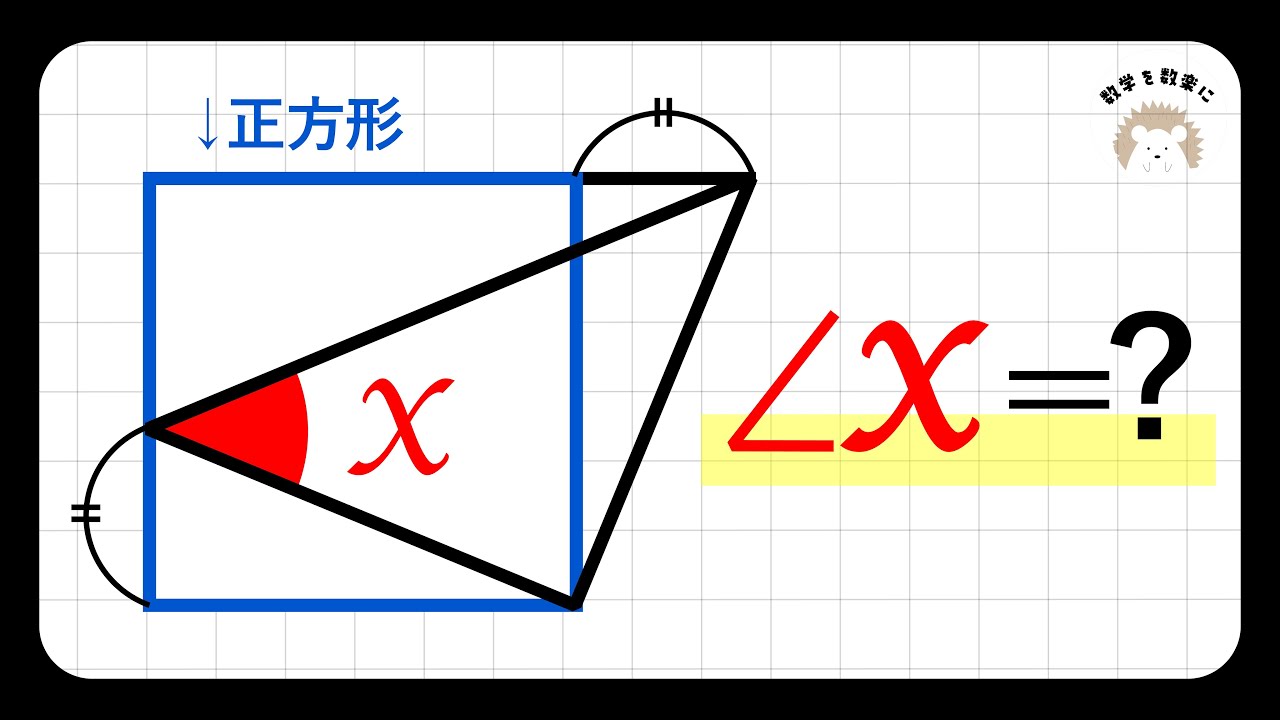
正方形と角度
【短時間でマスター!!】内接円や外接円と三角形に関する面積の求め方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
内接円や外接円と三角形に関する面積の求め方を解説します。
この動画を見る
数学1A
内接円や外接円と三角形に関する面積の求め方を解説します。
福田の1.5倍速演習〜合格する重要問題093〜中央大学2020年度理工学部第5問〜円周上の点と三角形五角形の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#微分法と積分法#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa >0,b >0, a +b<$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0<a<$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。
2020中央大学理工学部過去問
この動画を見る
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa >0,b >0, a +b<$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0<a<$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。
2020中央大学理工学部過去問
おうぎ形の面積 数学YouTuberが今流行りの数学YouTuberについて語る

【短時間でマスター!!】三角形の面積の求め方を解説!〔現役塾講師解説、数学〕

2023共通テスト 正弦定理で解く!?こんな解き方もあり?

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の半径=5
$sin\angle ACB = $
*図は動画内参照
2023共通テスト数ⅠA
この動画を見る
円の半径=5
$sin\angle ACB = $
*図は動画内参照
2023共通テスト数ⅠA
