 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
円の折り返し 北海 (南北海道)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
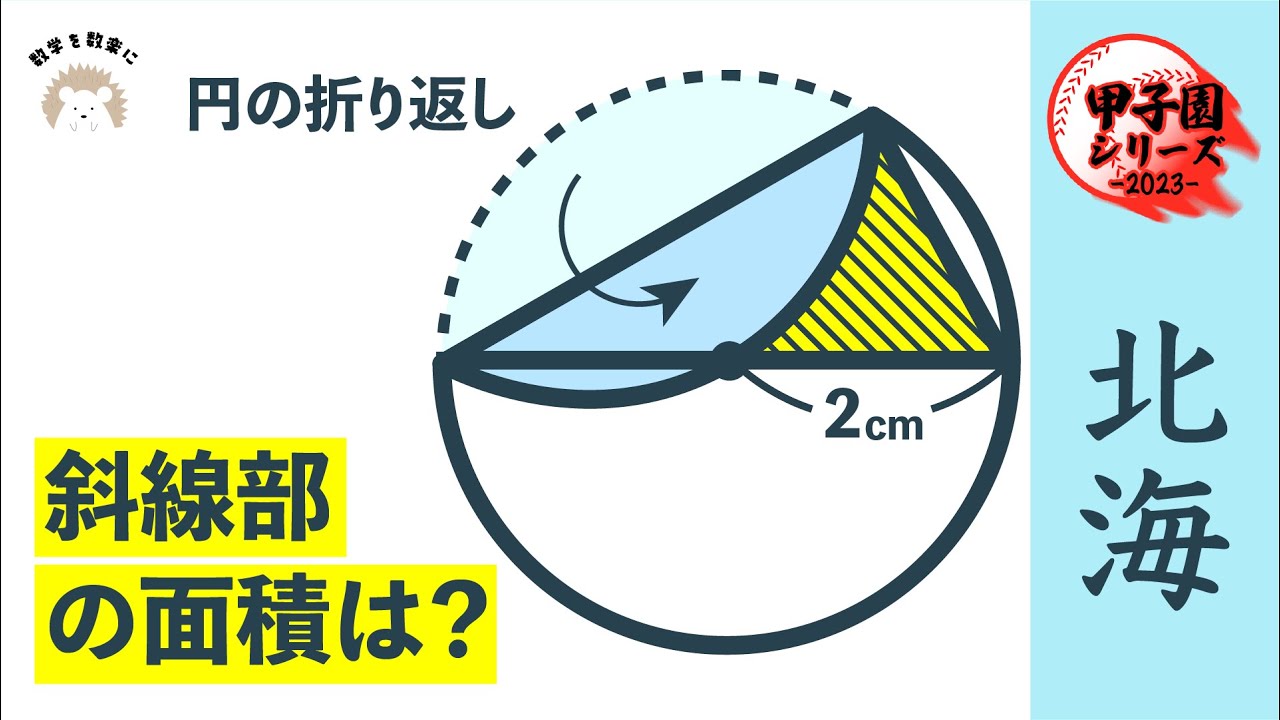
円の折り返し
斜線部の面積は?
*図は動画内参照
(南北海道)
この動画を見る
円の折り返し
斜線部の面積は?
*図は動画内参照
(南北海道)
因数分解 大垣日大 (岐阜)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x+y)(x+y+2)-8$
大垣日本大学高等学校
この動画を見る
因数分解せよ
$(x+y)(x+y+2)-8$
大垣日本大学高等学校
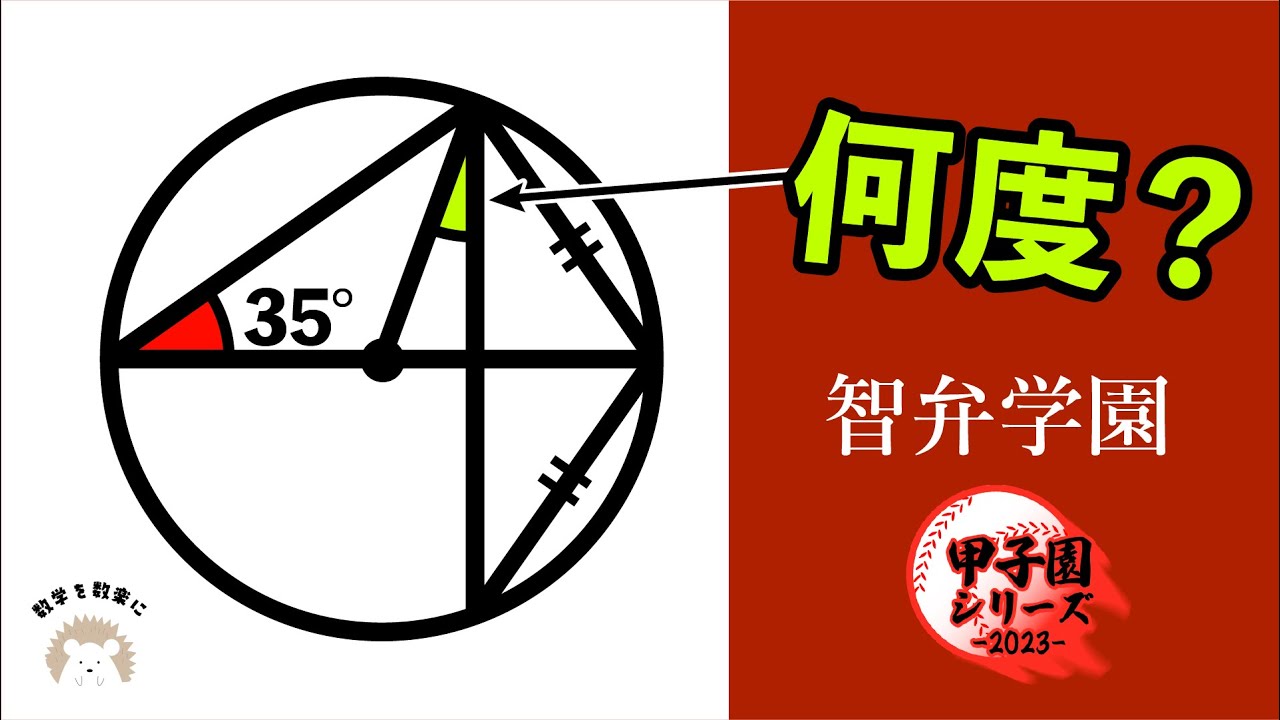
円周角 2通りで解説 智辯学園 (奈良)
中学生はよく間違えます。ルートを外せ!仙台育英(宮城県)

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{17-a}$の値が整数となる自然数aは何個?
仙台育英学園高等学校
この動画を見る
$\sqrt{17-a}$の値が整数となる自然数aは何個?
仙台育英学園高等学校
3乗根が綺麗になっちゃった

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a≧\frac{1}{8}$
$\sqrt[3]{a+\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}+\sqrt[3]{a-\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}$
の値を求めよ.
この動画を見る
$a≧\frac{1}{8}$
$\sqrt[3]{a+\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}+\sqrt[3]{a-\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}$
の値を求めよ.
3通りで解説!分母の有理化どうする? 高知中央 (高知)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 6 + \frac{18}{\sqrt 6}$
高知中央高等学校
この動画を見る
$\sqrt 6 + \frac{18}{\sqrt 6}$
高知中央高等学校
サラッと解説してますが、実際解くときは結構試行錯誤してます。円と角の二等分 土浦日大(茨城県)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
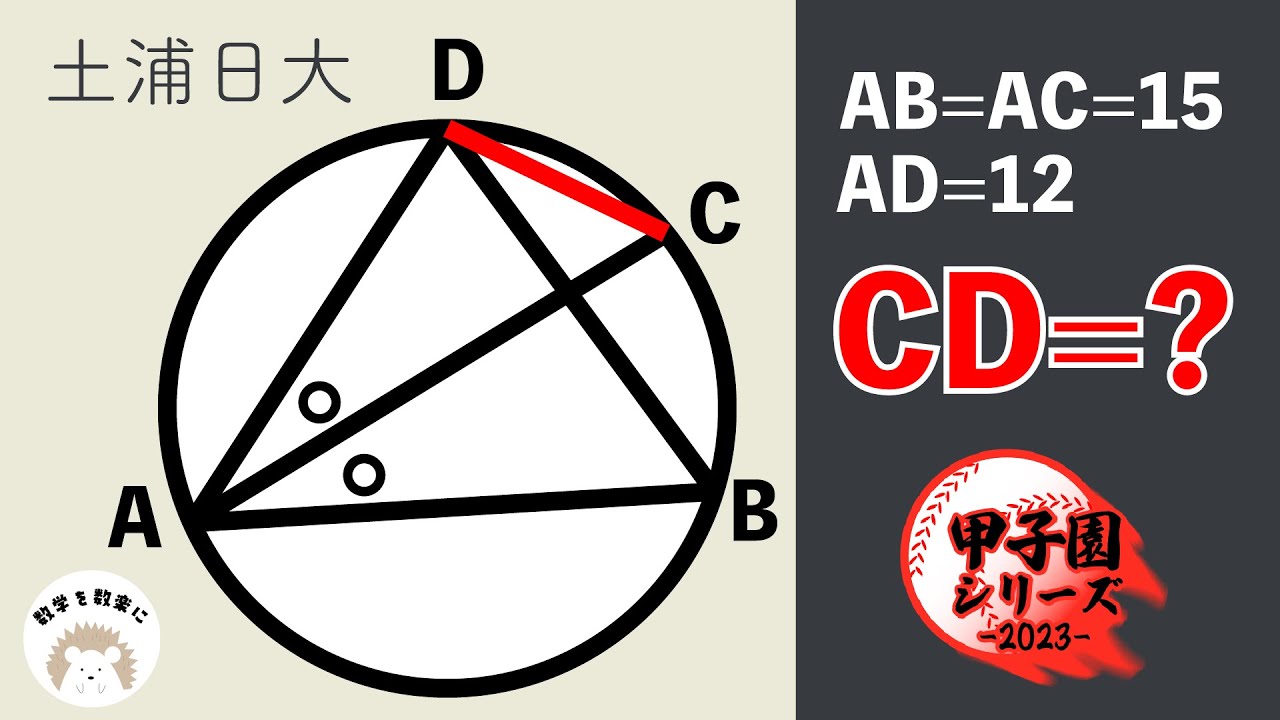
$AB=AC=15$
$AD=12$
$CD=?$
*図は動画内参照
土浦日本大学高等学校
この動画を見る
$AB=AC=15$
$AD=12$
$CD=?$
*図は動画内参照
土浦日本大学高等学校
面積比 九州国際大附属 (福岡県)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
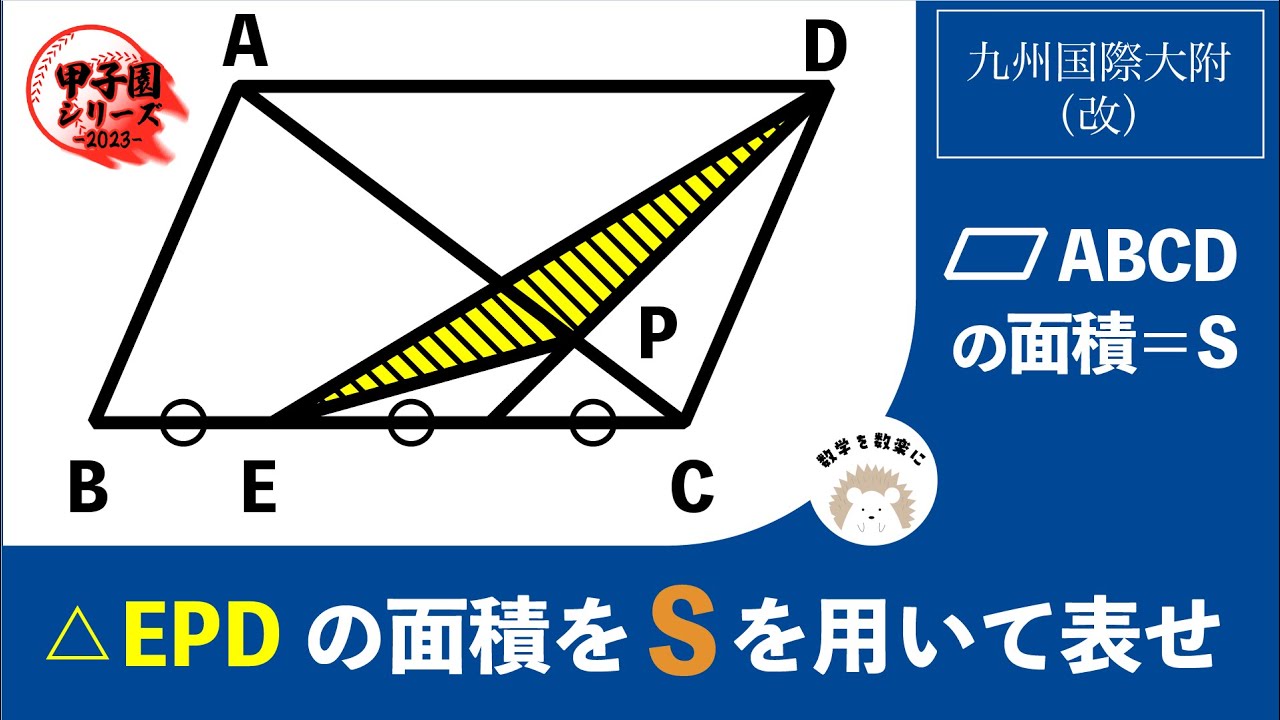
▱ABCDの面積=S
△EPDの面積をSを用いて表せ
*図は動画内参照
九州国際大学付属高等学校(改)
この動画を見る
▱ABCDの面積=S
△EPDの面積をSを用いて表せ
*図は動画内参照
九州国際大学付属高等学校(改)
福田の数学〜浜松医科大学2023年医学部第4問〜三角形と整数問題

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#整数の性質#三角形の辺の比(内分・外分・二等分線)#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $\triangle$ABCにおいて、BC=3, AC=$b$, AB=$c$, $\angle$ACB=$\theta$とする。$b$と$c$を素数とするとき、以下の問いに答えよ。
(1)$b$=3,$c$=5 のとき、$\cos\theta$の値を求めよ。
(2)$\cos\theta$<0 のとき、$c$=$b$+2 が成り立つことを示せ。
(3)$-\displaystyle\frac{5}{8}$<$\cos\theta$<$-\displaystyle\frac{7}{12}$ のとき、$b$と$c$の値の組をすべて求めよ。
この動画を見る
$\Large\boxed{4}$ $\triangle$ABCにおいて、BC=3, AC=$b$, AB=$c$, $\angle$ACB=$\theta$とする。$b$と$c$を素数とするとき、以下の問いに答えよ。
(1)$b$=3,$c$=5 のとき、$\cos\theta$の値を求めよ。
(2)$\cos\theta$<0 のとき、$c$=$b$+2 が成り立つことを示せ。
(3)$-\displaystyle\frac{5}{8}$<$\cos\theta$<$-\displaystyle\frac{7}{12}$ のとき、$b$と$c$の値の組をすべて求めよ。
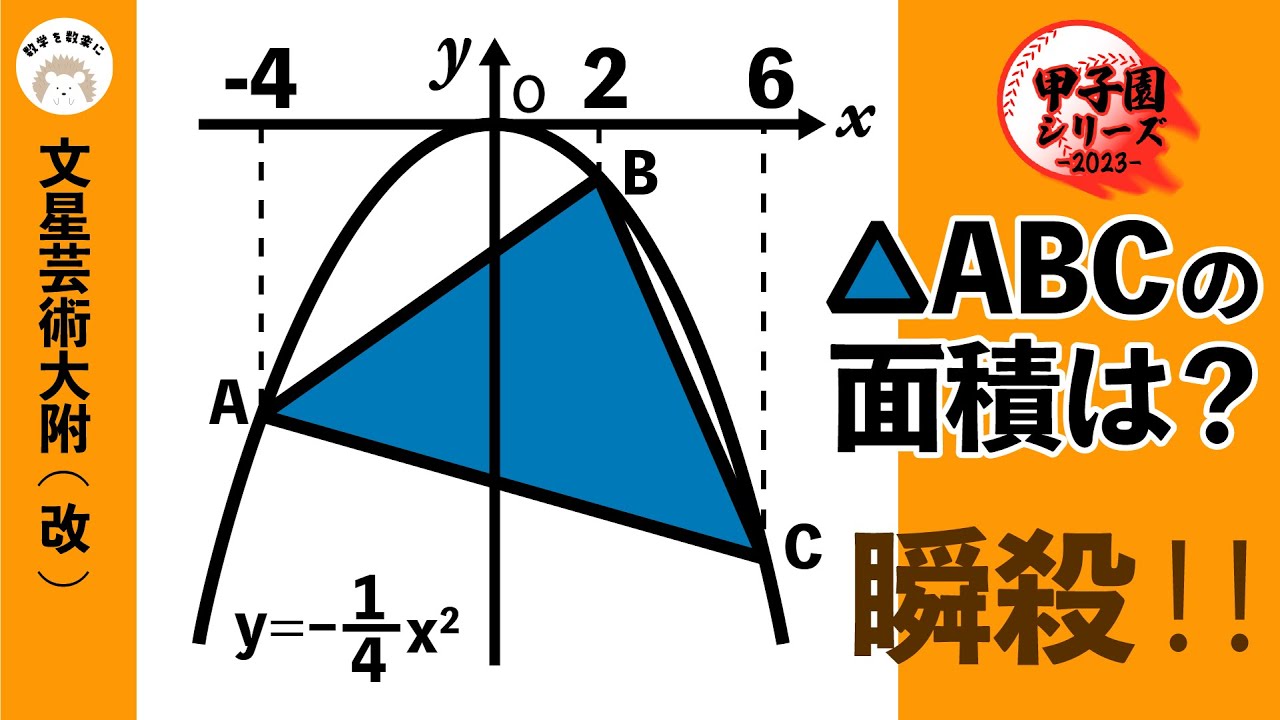
座標平面上の三角形の面積 文星芸術大附(改)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABCの面積は?
*図は動画内参照
文星芸術大学附属高等学校(改)
この動画を見る
△ABCの面積は?
*図は動画内参照
文星芸術大学附属高等学校(改)
和と差の積不要

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
和と差の積不要
分母を有理化せよ。
$\frac{3+\sqrt 3}{\sqrt 3 + 1}$
この動画を見る
和と差の積不要
分母を有理化せよ。
$\frac{3+\sqrt 3}{\sqrt 3 + 1}$
連立二元二次方程式
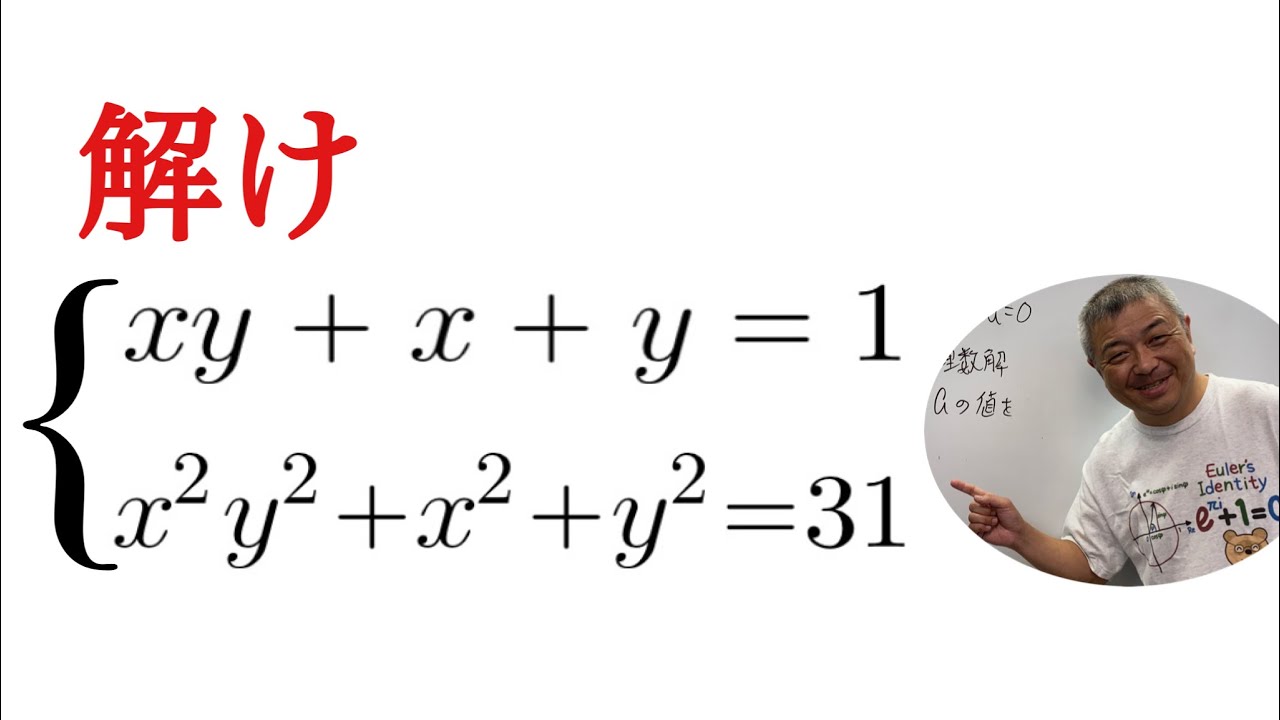
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
解け
\begin{eqnarray}
\left\{
\begin{array}{l}
xy + x + y = 1 \\
x^2y^2 + x^2 + y^2 = 31
\end{array}
\right.
\end{eqnarray}
この動画を見る
解け
\begin{eqnarray}
\left\{
\begin{array}{l}
xy + x + y = 1 \\
x^2y^2 + x^2 + y^2 = 31
\end{array}
\right.
\end{eqnarray}
因数分解は試してなんぼ。立命館宇治(京都)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2-4ab-3a+4b^2+6b$
立命館宇治高等学校
この動画を見る
因数分解せよ
$a^2-4ab-3a+4b^2+6b$
立命館宇治高等学校
2次関数 グラフと2次不等式4【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次関数$y=x^2+mx+2$が次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)この2次関数のグラフと$x$軸の正の部分が異なる2点で交わる。
(2)この2次関数のグラフと$x$軸の$x\lt -1$の部分が異なる2点で交わる。
放物線$y=x^2+2(m-1)x+5-m^2$が$x$軸の正の部分と負の部分のそれぞれと交わるように、定数$m$の値の範囲を定めよ。
2次方程式$x^2+2mx+2m+3=0$が次のような実数解をもつように、定数$m$の値の範囲を定めよ。
(1)異なる2つの負の解
(2)-4より大きい異なる2つの解
この動画を見る
2次関数$y=x^2+mx+2$が次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)この2次関数のグラフと$x$軸の正の部分が異なる2点で交わる。
(2)この2次関数のグラフと$x$軸の$x\lt -1$の部分が異なる2点で交わる。
放物線$y=x^2+2(m-1)x+5-m^2$が$x$軸の正の部分と負の部分のそれぞれと交わるように、定数$m$の値の範囲を定めよ。
2次方程式$x^2+2mx+2m+3=0$が次のような実数解をもつように、定数$m$の値の範囲を定めよ。
(1)異なる2つの負の解
(2)-4より大きい異なる2つの解
平均は足して2で割るもの。? 近江(滋賀)

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A組、B組の2クラスでテストを行った。
35人クラスのA組の平均点がa点
40人クラスのB組の平均点がb点
2クラス全体の平均点をa,bで表せ。
近江高等学校
この動画を見る
A組、B組の2クラスでテストを行った。
35人クラスのA組の平均点がa点
40人クラスのB組の平均点がb点
2クラス全体の平均点をa,bで表せ。
近江高等学校
正負を答えよ 大垣日大(改)(岐阜)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a>0 , b<0 , |a| < |b|のとき式の正負答えよ
(1)$a+b$
(2)$b^2-a^2$
(3)$\sqrt a - \sqrt{-b}$
大垣日本大学高等学校
この動画を見る
a>0 , b<0 , |a| < |b|のとき式の正負答えよ
(1)$a+b$
(2)$b^2-a^2$
(3)$\sqrt a - \sqrt{-b}$
大垣日本大学高等学校
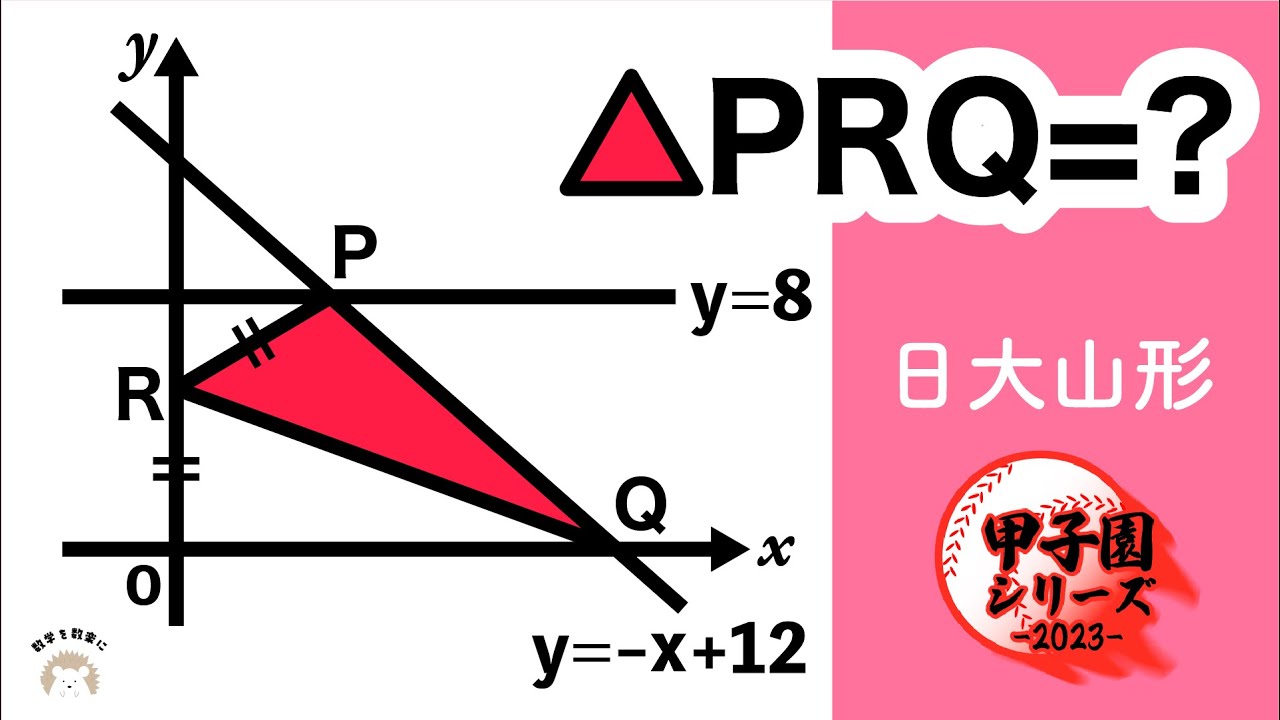
座標平面上の三角形 日大山形 (山形)
cosの和を求める

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の値
$
\cos{\frac{\pi}{7}}-\cos{\frac{2\pi}{7}}+\cos{\frac{3\pi}{7}}
$を求めよ.
この動画を見る
次の値
$
\cos{\frac{\pi}{7}}-\cos{\frac{2\pi}{7}}+\cos{\frac{3\pi}{7}}
$を求めよ.
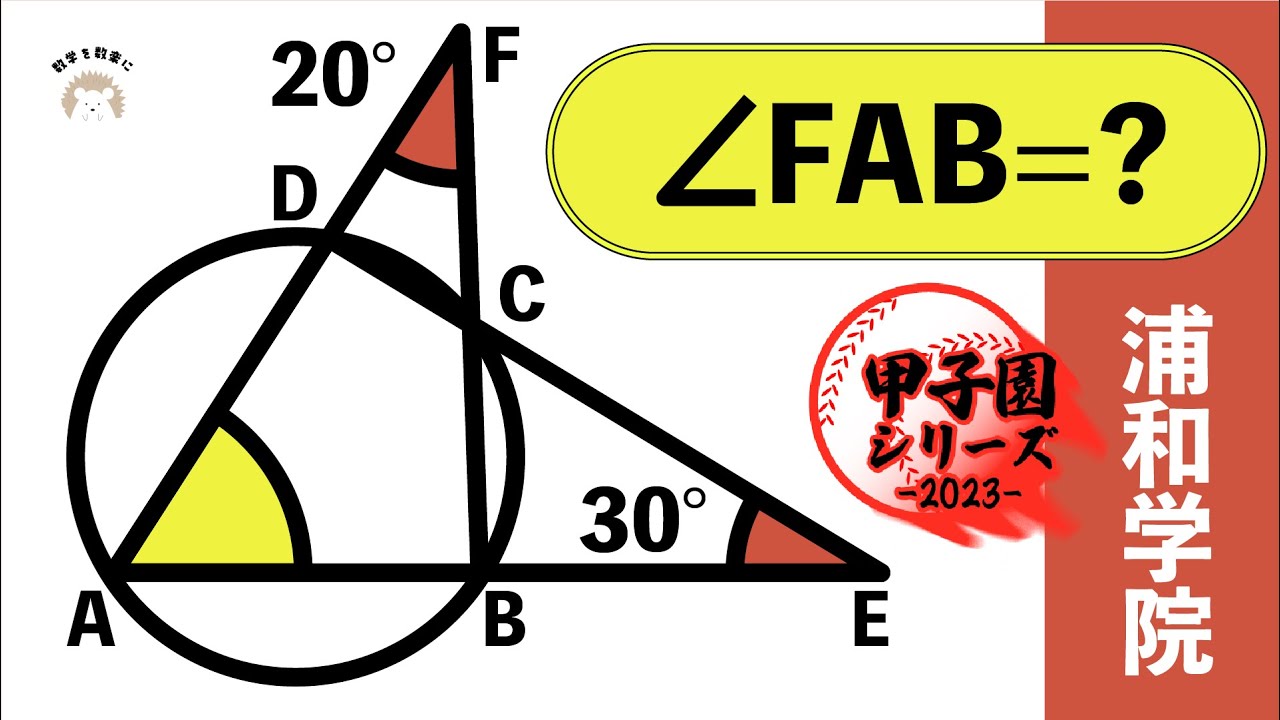
円とブーメランの角 浦和学院(埼玉)
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle FAB =?$
*図は動画内参照
浦和学院高等学校
この動画を見る
$\angle FAB =?$
*図は動画内参照
浦和学院高等学校
この球々はなんや?
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
絶対値のグラフの説明動画です
この動画を見る
絶対値のグラフの説明動画です
慣れたら暗算!?平方根の計算 土浦日大(茨城)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{\sqrt 5+ \sqrt 3}{2})^2(\frac{\sqrt 5 - \sqrt 3}{2})^2$
土浦日本大学高等学校
この動画を見る
$(\frac{\sqrt 5+ \sqrt 3}{2})^2(\frac{\sqrt 5 - \sqrt 3}{2})^2$
土浦日本大学高等学校
大学入試問題#608「絶対値・・・・」 横浜市立大学(2009) #定積分

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#三角関数#三角関数とグラフ#加法定理とその応用#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典:2009年横浜市立大学 入試問題
式の値 中学生の解き方 高校生の解き方
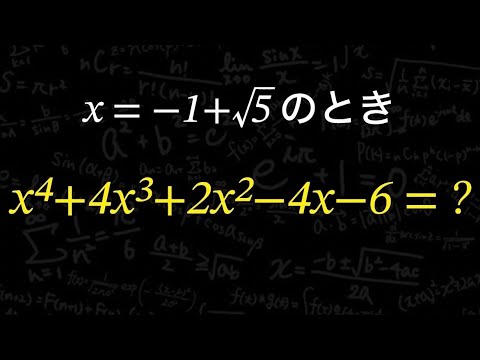
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=-1+\sqrt 5$のとき
$x^4+4x^3+2x^2-4x-6=?$
この動画を見る
$x=-1+\sqrt 5$のとき
$x^4+4x^3+2x^2-4x-6=?$
気付けば一瞬!!正方形と円

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△BODの面積は?
*図は動画内参照
この動画を見る
△BODの面積は?
*図は動画内参照
三角比の相互関係と符号の決め方について解説(数学Ⅰ)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$90^{ \circ } \lt \alpha \lt 180^{ \circ }$で$\sin\alpha=\displaystyle \frac{2}{5}$のとき、$\cos\alpha,\tan\alpha$の値を求めよ。
この動画を見る
$90^{ \circ } \lt \alpha \lt 180^{ \circ }$で$\sin\alpha=\displaystyle \frac{2}{5}$のとき、$\cos\alpha,\tan\alpha$の値を求めよ。
大学入試問題#606「見るからに落とせない気がする」 福島大学(2012) #方程式

単元:
#数Ⅰ#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x=\sqrt{ 2+\sqrt{ x^2-2 } }$を満たす実数$x$を求めよ
出典:2012年福島大学 入試問題
この動画を見る
$x=\sqrt{ 2+\sqrt{ x^2-2 } }$を満たす実数$x$を求めよ
出典:2012年福島大学 入試問題
福井大 漸化式と整数問題の融合

単元:
#数Ⅰ#整数の性質#約数・倍数・整数の割り算と余り・合同式#漸化式#数学(高校生)#福井大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2010福井大学過去問題
k,n自然数
$a_1=k$
$a_{n+1}=2a_n+1$
①$a_{n+4}-a_n$は15の倍数であることを示せ
②$a_{2010}$が15の倍数となる最小のk
この動画を見る
2010福井大学過去問題
k,n自然数
$a_1=k$
$a_{n+1}=2a_n+1$
①$a_{n+4}-a_n$は15の倍数であることを示せ
②$a_{2010}$が15の倍数となる最小のk
小学生向け問題
【短時間でマスター!!】連立2次不等式の書き方を解説!〔現役講師解説、数学〕

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + 3x + 2 > 0 \\
x^2 + 2x - 3 < 0
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + 3x + 2 > 0 \\
x^2 + 2x - 3 < 0
\end{array}
\right.
\end{eqnarray}$
【数学】2022年度 第2回 K塾記述高2模試 全問解説(ベクトルはおまけ)、※修正箇所:問1(1)(概要欄へ)

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#複素数と方程式#図形と計量#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#確率#図形と方程式#三角関数#複素数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度第2回全統記述高2模試全問解説動画です!
この動画を見る
2022年度第2回全統記述高2模試全問解説動画です!
