 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
神奈川県教員採用試験(2021)「解き方は何種類かありそう」 #関数

単元:
#2次関数#その他
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{x^2}{9}+y^2=1$を満たす$x,y$に対し$x+3y^2$の最小値を求めよ
出典:2021年神奈川県教員採用試験
この動画を見る
$\displaystyle \frac{x^2}{9}+y^2=1$を満たす$x,y$に対し$x+3y^2$の最小値を求めよ
出典:2021年神奈川県教員採用試験
素数問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
素数$(p,q)$の組をすべて求めよ.
$-p^3+4p^2+7p-1=q^2$
この動画を見る
素数$(p,q)$の組をすべて求めよ.
$-p^3+4p^2+7p-1=q^2$
2023高校入試解説10問目 二次方程式2023 日大習志野

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
この動画を見る
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
図で理解する2次方程式の解の公式~ほーみんに数学教えてみた~

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図で理解する2次方程式の解の公式~ほーみんに数学教えてみた~
この動画を見る
図で理解する2次方程式の解の公式~ほーみんに数学教えてみた~
大学入試問題#426「基本的な計算問題」 Instagram #三角関数
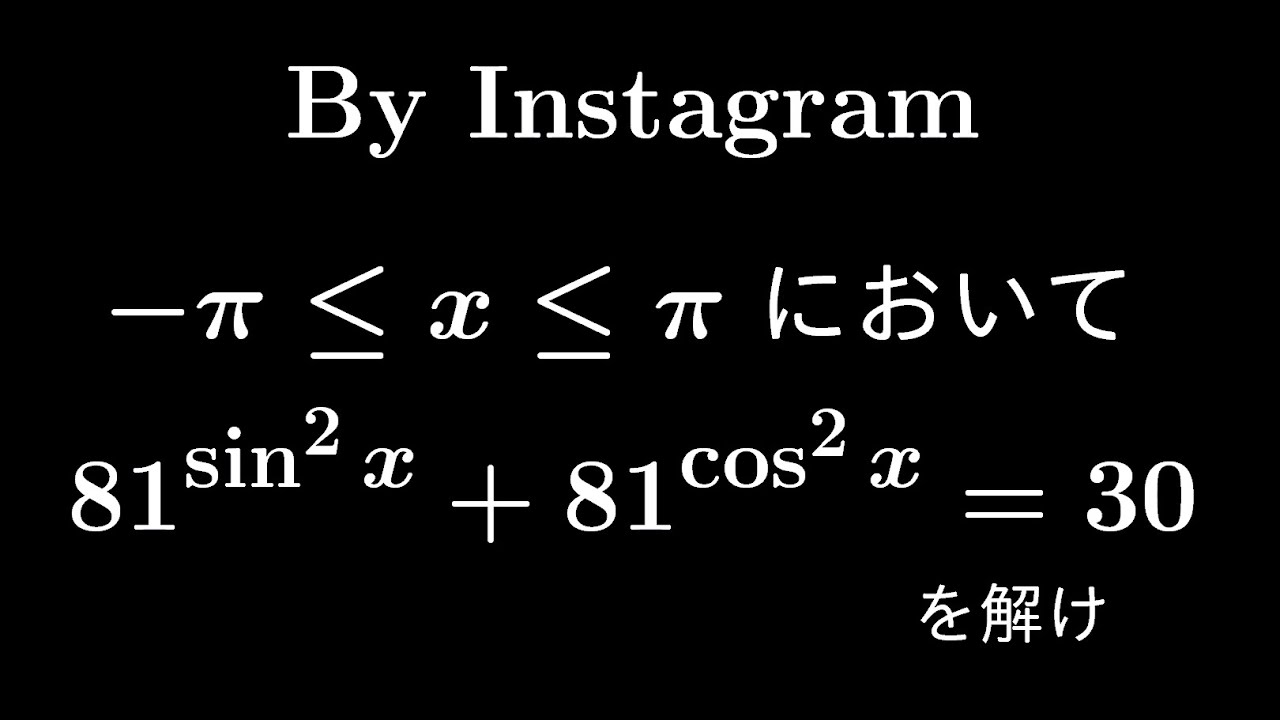
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$-\pi \leqq x \lt \pi$とする。
$81^{\sin^2x}+81^{\cos^2x}=30$
この動画を見る
$-\pi \leqq x \lt \pi$とする。
$81^{\sin^2x}+81^{\cos^2x}=30$
整数問題

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$32n^2$で割り切れることを示せ.
この動画を見る
nを自然数とする.
$(4n-1)^{2n+1}+(4n+1)^{2n-1}$は$32n^2$で割り切れることを示せ.
2023高校入試解説9問目 和と差の積は二乗の差 日大習志野

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(1+\sqrt 2)(1+\sqrt 8)(1-\frac{1}{\sqrt 2})(1-\frac{1}{\sqrt 8})$
2023日本大学習志野高等学校
この動画を見る
$(1+\sqrt 2)(1+\sqrt 8)(1-\frac{1}{\sqrt 2})(1-\frac{1}{\sqrt 8})$
2023日本大学習志野高等学校
二次関数の難問!大事な考え方【神戸大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a$を実数とし,$f(x)=-x^2-2x+2,g(x)=-x^2+ax+a$とする。以下の問いに答えよ。
(1)すべての実数$s,t$に対して$f(x)≧g(t)$が成り立つような,$a$の値の範囲を求めよ。
(2)$0≦x≦1を満たすすべての$x$に対して,$f(x)≧g(x)が成り立つような$a$の範囲を求めよ。
神戸大過去問
この動画を見る
$a$を実数とし,$f(x)=-x^2-2x+2,g(x)=-x^2+ax+a$とする。以下の問いに答えよ。
(1)すべての実数$s,t$に対して$f(x)≧g(t)$が成り立つような,$a$の値の範囲を求めよ。
(2)$0≦x≦1を満たすすべての$x$に対して,$f(x)≧g(x)が成り立つような$a$の範囲を求めよ。
神戸大過去問
共通テストだけど中学生も解ける!!
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
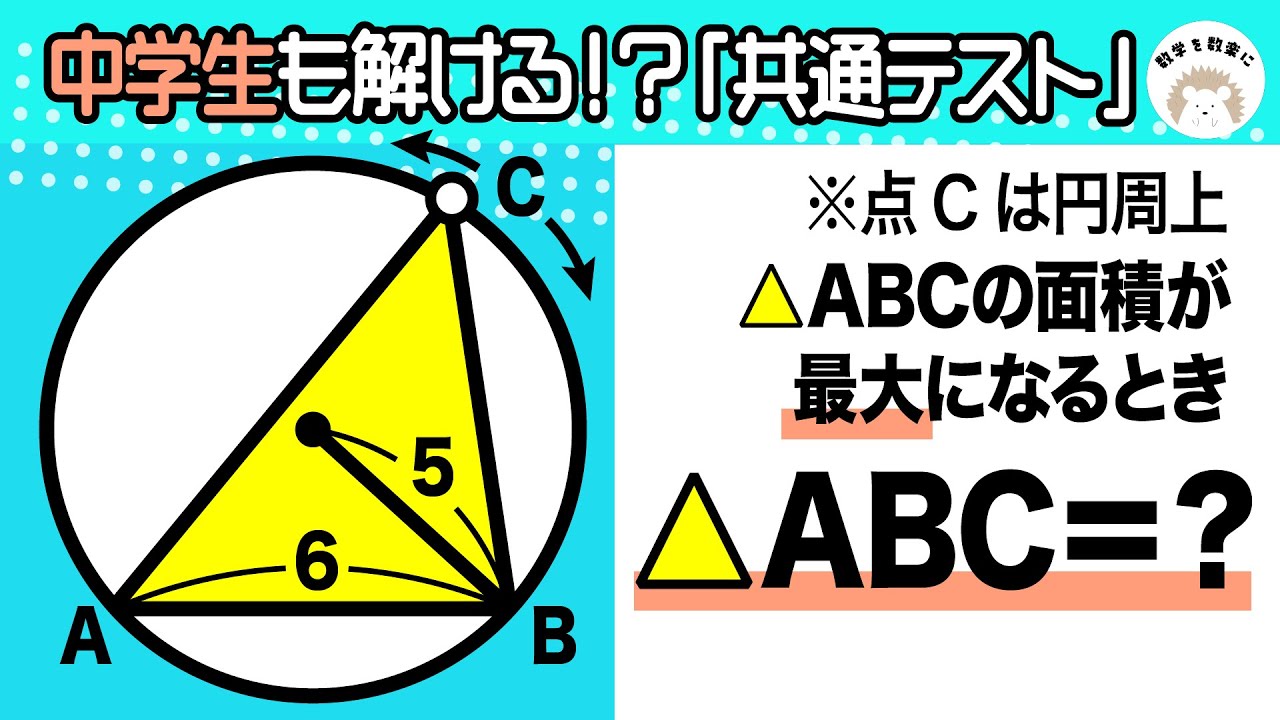
△ABCの面積が最大になるとき△ABC=?
*点Cは円周上
*図は動画内参照
2023共通テスト数ⅠA
この動画を見る
△ABCの面積が最大になるとき△ABC=?
*点Cは円周上
*図は動画内参照
2023共通テスト数ⅠA
福田の数学〜2023年共通テスト速報〜数学IA第2問データの分析と2次関数

単元:
#数Ⅰ#2次関数#データの分析#2次関数とグラフ#データの分析#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第2問
[1]太郎さんは総務省が公表している2020年の家計調査の結果を用いて、地域による食文化の違いについて考えている。家計調査における調査地点は、都道府県庁所在市および政令指定都市(都道府県庁所在市を除く)であり、合計52市である。家計調査の結果の中でも、スーパーマーケットなどで販売されている調理食品の「二人以上の世帯の1世帯当たり年間支出金額(以下、支出金額、単位は円)」を分析することにした。以下においては、52市の調理食品の支出金額をデータとして用いる。
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように(※動画参照)52市におけるかば焼きの支出金額のヒストグラムを作成した。
ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(1)図1から次のことが読み取れる。
・第1四分位数が含まれる階級は$\boxed{\boxed{\ \ ア\ \ }}$である。
・第3四分位数が含まれる階級は$\boxed{\boxed{\ \ イ\ \ }}$である。
・四分位範囲は$\boxed{\boxed{\ \ ウ\ \ }}$。
$\boxed{\boxed{\ \ ア\ \ }}$、$\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪1000以上1400未満 ①1400以上1800未満
②1800以上2200未満 ③2200以上2600未満
④2600以上3000未満 ⑤3000以上3400未満
⑥3400以上3800未満 ⑦3800以上4200未満
⑧4200以上4600未満 ⑨4600以上5000未満
$\boxed{\boxed{\ \ ウ\ \ }}$の解答群
⓪800より小さい
①800より大きく1600より小さい
②1600より大きく2400より小さい
③2400より大きく3200より小さい
④3200より大きく4000より小さい
⑤4000より大きい
(2)太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E(19市)と西側の地域W(33市)の二つに分けて考えることにした。
(i)地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図2,図3のように(※動画参照)それぞれ作成した。
かば焼きの支出金額について、図2と図3から読み取れることとして、次の⓪~③のうち、
正しいものは$\boxed{\boxed{\ \ エ\ \ }}$である。
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪地域Eにおいて、小さい方から5番目は2000以下である。
①地域Eと地域Wの範囲は等しい。
②中央値は、地域Eより地域Wの方が大きい。
③2600未満の市の割合は、地域Eより地域Wの方が大きい。
(ii)太郎さんは、地域Eと地域Wのデータの散らばりの度合いを数値でとらえようと思い、
それぞれの分散を考えることにした。地域Eにおけるかば焼きの支出金額の分散は、地域Eのそれぞれの市におけるかば焼きの支出金額の偏差の$\boxed{\boxed{\ \ オ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪2乗を合計した値
①絶対値を合計した値
②2乗を合計して地域Eのの市の数で割った値
③絶対値を合計して地域Eの市の数で割った値
④2乗を合計して地域Eの市の数で割った値の平方根のうち正のもの
⑤絶対値を合計して地域Eの市の数で割った値の平方根のうち正のもの
(3)太郎さんは、(2)で考えた地域Eにおける、やきとりの支出金額についても調べることにした。
ここでは地域Eにおいて、やきとりの支出金額が増加すれば、かば焼きの支出金額も増加する傾向があるのではないかと考え、まず図4(※動画参照)のように、地域Eにおける、やきとりとかば焼きの支出金額の散布図を作成した。そして、相関係数を計算するために、表1(※動画参照)のように平均値、分散、標準偏差および共分散を算出した。ただし、共分散は地域Eのそれぞれの市における、やきとりの支出金額の偏差とかば焼きの支出金額の偏差との積の平均値である。
表1を用いると、地域Eにおける、やきとりの支出金額とかば焼きの支出金額の相関係数は$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ カ\ \ }}$については、最も適当なものを、次の⓪~⑨のうちから一つ選べ。
⓪-0.62 ①-0.50②-0.37③-0.19
④-0.02⑤0.02⑥0.19⑦0.37
⑧0.50⑨0.62
[2]太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
二人は、図1(※動画参照)のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図を描き、ボールがリング入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
【仮定】
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点A(3.8, 3),右端を点B(4.2, 3)とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M(4, 3)を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離が0.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに点$P_0$(0, 3)にあるものとする。また、$P_0$,Mを通る、上に凸の放物線を$C_1$とし、Pは$C_1$上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Hとし、Hは、はじめに点$H_0$(0, 2)にあるものとする。また、$H_0$, Mを通る、上に凸の放物線を$C_2$とし、Hは$C_2$上を動くものとする。
・放物線$C_1$や$C_2$に対して、頂点のy座標を「シュートの高さ」とし、頂点のx座標を「ボールが最も高くなるときの地上の位置」とする。
(1)放物線$C_1$の方程式における$x^2$の係数をaとする。放物線$C_1$の方程式は
y=a$x^2$-$\boxed{\ \ キ\ \ }$ax+$\boxed{\ \ ク\ \ }$
と表すことができる。また、プロ選手の「シュートの高さ」は
-$\boxed{\ \ ケ\ \ }$a+$\boxed{\ \ コ\ \ }$
である。
放物線$C_2$の方程式における$x^2$の係数をpとする。放物線$C_2$の方程式は
y=p$\left\{x-\left(2-\frac{1}{8p}\right)\right\}^2-\frac{(16p-1)^2}{64p}+2$
と表すことができる。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、次の⓪~③のうち、正しいものは$\boxed{\boxed{\ \ サ\ \ }}$である。
$\boxed{\boxed{\ \ サ\ \ }}$の解答群
⓪プロ選手と花子さんの「ボールが最も高くなる時の地上の位置」は、常に一致する。
①プロ選手の「ボールが最も高くなるときの地上の位置」の方が、常にMのx座標に近い。
②花子選手の「ボールが最も高くなるときの地上の位置」の方が、常にMのx座標に近い。
③プロ選手の「ボールが最も高くなるときの地上の位置」の方がMのx座標に近いときもあれば、花子さんの「ボールが最も高くなるときの地上の位置」の方が、Mのx座標に近いときもある。
(2)二人は、ボールがリングすれすれを通る場合のプロ選手と花子さんの「シュートの高さ」について次のように話している。
太郎:例えば、プロ選手のボールがリングに当たらないようにするには、Pがリングの左端Aのどのくらい上を通れば良いのかな。
花子:Aの真上の点でPが通る点Dを、線分DMがAを中心とする半径0.1の円と接するようにとって考えてみたらどうかな。
太郎:なるほど。Pの軌道は上に凸の放物線で山なりだから、その場合、図2(※動画参照)のように、PはDを通った後で線分DMより上側を通るのでボールはリングに当たらないね。花子さんの場合も、HがこのDを通れば、ボールはリングに当たらないね。
花子:放物線$C_1$と$C_2$がDを通る場合でプロ選手と私の「シュートの高さ」を比べってみようよ。
図2のように、Mを通る直線lが、Aを中心とする半径0.1の円に直線ABの上側で接しているとする。また、Aを通り直線ABに垂直な直線を引き、lとの交点をDとする。このとき、AD=$\frac{\sqrt 3}{15}$である。
よって、放物線$C_1$がDを通るとき、$C_1$の方程式は
y=-$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セソ\ \ }}\left(x^2-\boxed{\ \ キ\ \ }x\right)+\boxed{\ \ ク\ \ }$
となる。
2023共通テスト過去問
この動画を見る
第2問
[1]太郎さんは総務省が公表している2020年の家計調査の結果を用いて、地域による食文化の違いについて考えている。家計調査における調査地点は、都道府県庁所在市および政令指定都市(都道府県庁所在市を除く)であり、合計52市である。家計調査の結果の中でも、スーパーマーケットなどで販売されている調理食品の「二人以上の世帯の1世帯当たり年間支出金額(以下、支出金額、単位は円)」を分析することにした。以下においては、52市の調理食品の支出金額をデータとして用いる。
太郎さんは調理食品として、最初にうなぎのかば焼き(以下、かば焼き)に着目し、図1のように(※動画参照)52市におけるかば焼きの支出金額のヒストグラムを作成した。
ただし、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
なお、以下の図や表については、総務省のWebページをもとに作成している。
(1)図1から次のことが読み取れる。
・第1四分位数が含まれる階級は$\boxed{\boxed{\ \ ア\ \ }}$である。
・第3四分位数が含まれる階級は$\boxed{\boxed{\ \ イ\ \ }}$である。
・四分位範囲は$\boxed{\boxed{\ \ ウ\ \ }}$。
$\boxed{\boxed{\ \ ア\ \ }}$、$\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪1000以上1400未満 ①1400以上1800未満
②1800以上2200未満 ③2200以上2600未満
④2600以上3000未満 ⑤3000以上3400未満
⑥3400以上3800未満 ⑦3800以上4200未満
⑧4200以上4600未満 ⑨4600以上5000未満
$\boxed{\boxed{\ \ ウ\ \ }}$の解答群
⓪800より小さい
①800より大きく1600より小さい
②1600より大きく2400より小さい
③2400より大きく3200より小さい
④3200より大きく4000より小さい
⑤4000より大きい
(2)太郎さんは、東西での地域による食文化の違いを調べるために、52市を東側の地域E(19市)と西側の地域W(33市)の二つに分けて考えることにした。
(i)地域Eと地域Wについて、かば焼きの支出金額の箱ひげ図を、図2,図3のように(※動画参照)それぞれ作成した。
かば焼きの支出金額について、図2と図3から読み取れることとして、次の⓪~③のうち、
正しいものは$\boxed{\boxed{\ \ エ\ \ }}$である。
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪地域Eにおいて、小さい方から5番目は2000以下である。
①地域Eと地域Wの範囲は等しい。
②中央値は、地域Eより地域Wの方が大きい。
③2600未満の市の割合は、地域Eより地域Wの方が大きい。
(ii)太郎さんは、地域Eと地域Wのデータの散らばりの度合いを数値でとらえようと思い、
それぞれの分散を考えることにした。地域Eにおけるかば焼きの支出金額の分散は、地域Eのそれぞれの市におけるかば焼きの支出金額の偏差の$\boxed{\boxed{\ \ オ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪2乗を合計した値
①絶対値を合計した値
②2乗を合計して地域Eのの市の数で割った値
③絶対値を合計して地域Eの市の数で割った値
④2乗を合計して地域Eの市の数で割った値の平方根のうち正のもの
⑤絶対値を合計して地域Eの市の数で割った値の平方根のうち正のもの
(3)太郎さんは、(2)で考えた地域Eにおける、やきとりの支出金額についても調べることにした。
ここでは地域Eにおいて、やきとりの支出金額が増加すれば、かば焼きの支出金額も増加する傾向があるのではないかと考え、まず図4(※動画参照)のように、地域Eにおける、やきとりとかば焼きの支出金額の散布図を作成した。そして、相関係数を計算するために、表1(※動画参照)のように平均値、分散、標準偏差および共分散を算出した。ただし、共分散は地域Eのそれぞれの市における、やきとりの支出金額の偏差とかば焼きの支出金額の偏差との積の平均値である。
表1を用いると、地域Eにおける、やきとりの支出金額とかば焼きの支出金額の相関係数は$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ カ\ \ }}$については、最も適当なものを、次の⓪~⑨のうちから一つ選べ。
⓪-0.62 ①-0.50②-0.37③-0.19
④-0.02⑤0.02⑥0.19⑦0.37
⑧0.50⑨0.62
[2]太郎さんと花子さんは、バスケットボールのプロ選手の中には、リングと同じ高さでシュートを打てる人がいることを知り、シュートを打つ高さによってボールの軌道がどう変わるかについて考えている。
二人は、図1(※動画参照)のように座標軸が定められた平面上に、プロ選手と花子さんがシュートを打つ様子を真横から見た図を描き、ボールがリング入った場合について、後の仮定を設定して考えることにした。長さの単位はメートルであるが、以下では省略する。
【仮定】
・平面上では、ボールを直径0.2の円とする。
・リングを真横から見たときの左端を点A(3.8, 3),右端を点B(4.2, 3)とし、リングの太さは無視する。
・ボールがリングや他のものに当たらずに上からリングを通り、かつ、ボールの中心がABの中点M(4, 3)を通る場合を考える。ただし、ボールがリングに当たるとは、ボールの中心とAまたはBとの距離が0.1以下になることとする。
・プロ選手がシュートを打つ場合のボールの中心を点Pとし、Pは、はじめに点$P_0$(0, 3)にあるものとする。また、$P_0$,Mを通る、上に凸の放物線を$C_1$とし、Pは$C_1$上を動くものとする。
・花子さんがシュートを打つ場合のボールの中心を点Hとし、Hは、はじめに点$H_0$(0, 2)にあるものとする。また、$H_0$, Mを通る、上に凸の放物線を$C_2$とし、Hは$C_2$上を動くものとする。
・放物線$C_1$や$C_2$に対して、頂点のy座標を「シュートの高さ」とし、頂点のx座標を「ボールが最も高くなるときの地上の位置」とする。
(1)放物線$C_1$の方程式における$x^2$の係数をaとする。放物線$C_1$の方程式は
y=a$x^2$-$\boxed{\ \ キ\ \ }$ax+$\boxed{\ \ ク\ \ }$
と表すことができる。また、プロ選手の「シュートの高さ」は
-$\boxed{\ \ ケ\ \ }$a+$\boxed{\ \ コ\ \ }$
である。
放物線$C_2$の方程式における$x^2$の係数をpとする。放物線$C_2$の方程式は
y=p$\left\{x-\left(2-\frac{1}{8p}\right)\right\}^2-\frac{(16p-1)^2}{64p}+2$
と表すことができる。
プロ選手と花子さんの「ボールが最も高くなるときの地上の位置」の比較の記述として、次の⓪~③のうち、正しいものは$\boxed{\boxed{\ \ サ\ \ }}$である。
$\boxed{\boxed{\ \ サ\ \ }}$の解答群
⓪プロ選手と花子さんの「ボールが最も高くなる時の地上の位置」は、常に一致する。
①プロ選手の「ボールが最も高くなるときの地上の位置」の方が、常にMのx座標に近い。
②花子選手の「ボールが最も高くなるときの地上の位置」の方が、常にMのx座標に近い。
③プロ選手の「ボールが最も高くなるときの地上の位置」の方がMのx座標に近いときもあれば、花子さんの「ボールが最も高くなるときの地上の位置」の方が、Mのx座標に近いときもある。
(2)二人は、ボールがリングすれすれを通る場合のプロ選手と花子さんの「シュートの高さ」について次のように話している。
太郎:例えば、プロ選手のボールがリングに当たらないようにするには、Pがリングの左端Aのどのくらい上を通れば良いのかな。
花子:Aの真上の点でPが通る点Dを、線分DMがAを中心とする半径0.1の円と接するようにとって考えてみたらどうかな。
太郎:なるほど。Pの軌道は上に凸の放物線で山なりだから、その場合、図2(※動画参照)のように、PはDを通った後で線分DMより上側を通るのでボールはリングに当たらないね。花子さんの場合も、HがこのDを通れば、ボールはリングに当たらないね。
花子:放物線$C_1$と$C_2$がDを通る場合でプロ選手と私の「シュートの高さ」を比べってみようよ。
図2のように、Mを通る直線lが、Aを中心とする半径0.1の円に直線ABの上側で接しているとする。また、Aを通り直線ABに垂直な直線を引き、lとの交点をDとする。このとき、AD=$\frac{\sqrt 3}{15}$である。
よって、放物線$C_1$がDを通るとき、$C_1$の方程式は
y=-$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セソ\ \ }}\left(x^2-\boxed{\ \ キ\ \ }x\right)+\boxed{\ \ ク\ \ }$
となる。
2023共通テスト過去問
中学入試だけど、二次方程式使って解いちゃった 灘中2023
単元:
#算数(中学受験)#数Ⅰ#2次関数#2次方程式と2次不等式#過去問解説(学校別)#平面図形#図形の移動#平面図形その他
指導講師:
数学を数楽に
問題文全文(内容文):
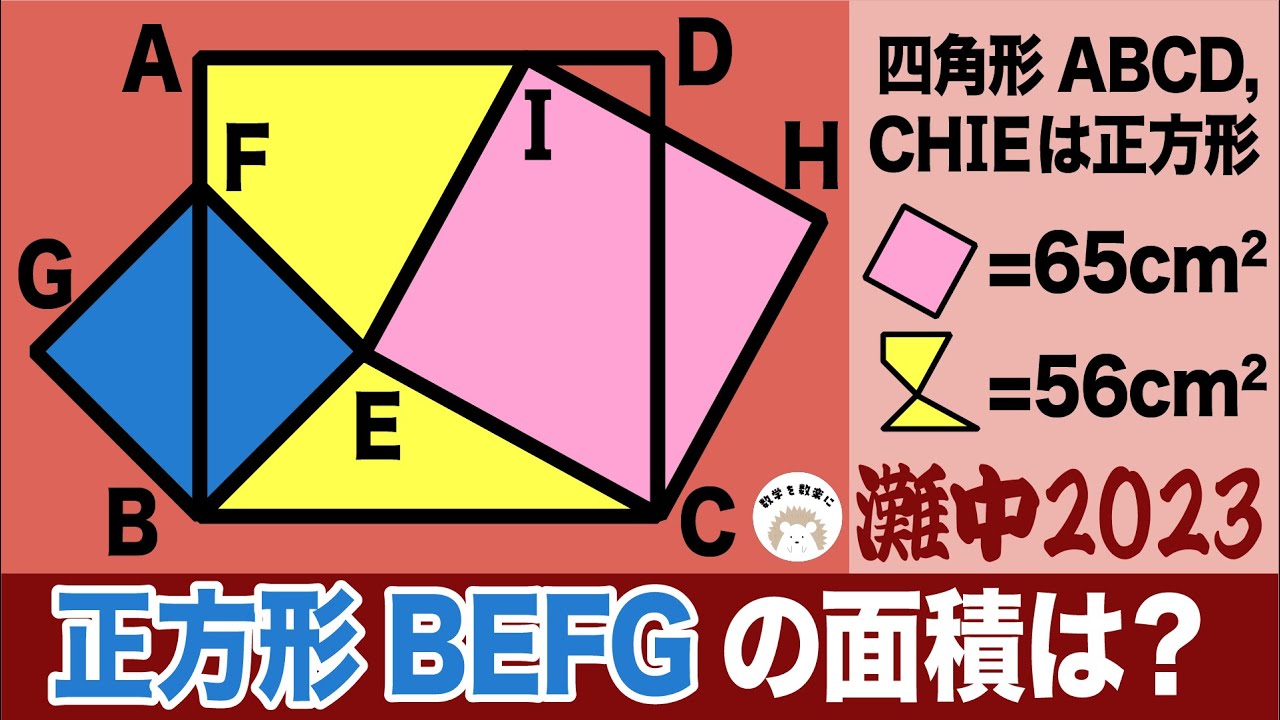
四角形ABCD、CHIEは正方形
正方形BEFGの面積=?
*図は動画内参照
2023灘中学校
この動画を見る
四角形ABCD、CHIEは正方形
正方形BEFGの面積=?
*図は動画内参照
2023灘中学校
福田の数学〜2023年共通テスト速報〜数学IA第1問不等式の解と図形の計量

単元:
#数Ⅰ#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第1問
[1]実数xについての不等式
|$x$+6| $\leqq$ 2
の解は
$\boxed{\ \ アイ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }$
である。
よって、実数$a,b,c,d$が
|(1-$\sqrt3$)($a-b$)($c-d$)+6| $\leqq$2
を満たしているとき、1-$\sqrt3$は負であることに注意すると、($a-b$)($c-d$)
の取り得る値の範囲は
$\boxed{\ \ オ\ \ }+\boxed{\ \ カ\ \ }\sqrt3 \leqq (a-b)(c-d) \leqq \boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3$
であることがわかる。
特に
$(a-b)(c-d)=\boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3 \cdots①$
であるとき、さらに
$(a-c)(b-d)=-3+\sqrt3 \cdots②$
が成り立つならば
$(a-d)(c-b)=\boxed{\ \ ケ\ \ }+\boxed{\ \ コ\ \ }\sqrt3 \cdots③$
であることが、等式①,②,③の左辺を展開して比較することによりわかる。
[2]
(1)点Oを中心とし、半径が5である円Oがある。この円周上に2点A,B
をAB=6となるようにとる。また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
(i)$\sin\angle ACB=\boxed{\boxed{\ \ サ\ \ }}$である。また、点Cを\angle ACBが鈍角となるようにとるとき、$\cos\angle ACB=\boxed{\boxed{\ \ シ\ \ }}$である。
(ii)点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直線ABに垂直な直線を引き、直線ABとの交点をDとするとき、
$\tan\angle OAD=\boxed{\boxed{\ \ ス\ \ }}$である。また、$\triangle ABC$の面積は$\boxed{\ \ セソ\ \ }$である。
$\boxed{\boxed{\ \ サ\ \ }}$ ~ $\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返し選んでもよい)
⓪$\displaystyle\frac{3}{5}$ ①$\displaystyle\frac{3}{4}$ ②$\displaystyle\frac{4}{5}$ ③ 1④$\displaystyle\frac{4}{3}$
⑤$-\displaystyle\frac{3}{5}$ ⑥$-\displaystyle\frac{3}{4}$ ⑦$-\displaystyle\frac{4}{5}$ ⑧ -1⑨$-\displaystyle\frac{4}{3}$
(2)半径が5である球Sがある。この球面上に3点P,Q,Rをとったとき、
これらの3点を通る平面α上でPQ=8, QR=5, RP=9であったとする。
球Sの球面上に点Tを三角錐TPQRの体積が最大となるようにとるとき、その体積を
求めよう。
まず、$\cos\angle QPR=\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}$である
ことから、$\triangle PQR$の面積は$\boxed{\ \ ツ\ \ }\sqrt{\boxed{\ \ テト\ \ }}$である。
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH,QH,RHの長さについて、$\boxed{\boxed{\ \ ナ\ \ }}$が成り立つ。
以上より、三角錐TPQRの体積は$\boxed{\ \ ニヌ\ \ }\left(\sqrt{\boxed{\ \ ネノ\ \ }}+\sqrt{\boxed{\ \ ハ\ \ }}\right)$である。
$\boxed{\boxed{\ \ ナ\ \ }}$の解答群
⓪PH<QH<RH ①PH<RH<QH
②QH<PH<RH ③QH<RH<PH
④RH<PH<QH ⑤RH<QH<PH
⑥PH=QH=RH
2023共通テスト過去問
この動画を見る
第1問
[1]実数xについての不等式
|$x$+6| $\leqq$ 2
の解は
$\boxed{\ \ アイ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }$
である。
よって、実数$a,b,c,d$が
|(1-$\sqrt3$)($a-b$)($c-d$)+6| $\leqq$2
を満たしているとき、1-$\sqrt3$は負であることに注意すると、($a-b$)($c-d$)
の取り得る値の範囲は
$\boxed{\ \ オ\ \ }+\boxed{\ \ カ\ \ }\sqrt3 \leqq (a-b)(c-d) \leqq \boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3$
であることがわかる。
特に
$(a-b)(c-d)=\boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3 \cdots①$
であるとき、さらに
$(a-c)(b-d)=-3+\sqrt3 \cdots②$
が成り立つならば
$(a-d)(c-b)=\boxed{\ \ ケ\ \ }+\boxed{\ \ コ\ \ }\sqrt3 \cdots③$
であることが、等式①,②,③の左辺を展開して比較することによりわかる。
[2]
(1)点Oを中心とし、半径が5である円Oがある。この円周上に2点A,B
をAB=6となるようにとる。また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
(i)$\sin\angle ACB=\boxed{\boxed{\ \ サ\ \ }}$である。また、点Cを\angle ACBが鈍角となるようにとるとき、$\cos\angle ACB=\boxed{\boxed{\ \ シ\ \ }}$である。
(ii)点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直線ABに垂直な直線を引き、直線ABとの交点をDとするとき、
$\tan\angle OAD=\boxed{\boxed{\ \ ス\ \ }}$である。また、$\triangle ABC$の面積は$\boxed{\ \ セソ\ \ }$である。
$\boxed{\boxed{\ \ サ\ \ }}$ ~ $\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返し選んでもよい)
⓪$\displaystyle\frac{3}{5}$ ①$\displaystyle\frac{3}{4}$ ②$\displaystyle\frac{4}{5}$ ③ 1④$\displaystyle\frac{4}{3}$
⑤$-\displaystyle\frac{3}{5}$ ⑥$-\displaystyle\frac{3}{4}$ ⑦$-\displaystyle\frac{4}{5}$ ⑧ -1⑨$-\displaystyle\frac{4}{3}$
(2)半径が5である球Sがある。この球面上に3点P,Q,Rをとったとき、
これらの3点を通る平面α上でPQ=8, QR=5, RP=9であったとする。
球Sの球面上に点Tを三角錐TPQRの体積が最大となるようにとるとき、その体積を
求めよう。
まず、$\cos\angle QPR=\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}$である
ことから、$\triangle PQR$の面積は$\boxed{\ \ ツ\ \ }\sqrt{\boxed{\ \ テト\ \ }}$である。
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH,QH,RHの長さについて、$\boxed{\boxed{\ \ ナ\ \ }}$が成り立つ。
以上より、三角錐TPQRの体積は$\boxed{\ \ ニヌ\ \ }\left(\sqrt{\boxed{\ \ ネノ\ \ }}+\sqrt{\boxed{\ \ ハ\ \ }}\right)$である。
$\boxed{\boxed{\ \ ナ\ \ }}$の解答群
⓪PH<QH<RH ①PH<RH<QH
②QH<PH<RH ③QH<RH<PH
④RH<PH<QH ⑤RH<QH<PH
⑥PH=QH=RH
2023共通テスト過去問
2023共通テスト数学 1A 第1問

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)#共通テスト
指導講師:
鈴木貫太郎
問題文全文(内容文):
第一問,
$\vert x+6 \vert \leqq 2$
$\Box \leqq x \leqq \Box$
$\vert (1-\sqrt3)(a-b)(c-d)+6 \vert 2$
$\Box \leqq (a-b)(c-d) \leqq \boxed{①}$
$(a-b)(c-d)=①$でさらに$(a-c)(b-d)=-3+\sqrt3 $なら $(a-d)(c-b)=\Box $
20232共通テスト過去問
この動画を見る
第一問,
$\vert x+6 \vert \leqq 2$
$\Box \leqq x \leqq \Box$
$\vert (1-\sqrt3)(a-b)(c-d)+6 \vert 2$
$\Box \leqq (a-b)(c-d) \leqq \boxed{①}$
$(a-b)(c-d)=①$でさらに$(a-c)(b-d)=-3+\sqrt3 $なら $(a-d)(c-b)=\Box $
20232共通テスト過去問
2023高校入試解説7問目 工夫して解け2次方程式 早稲田佐賀

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
この動画を見る
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
42を素因数分解の正答率 全国学力調査

大阪公立大 7の80乗の下5桁

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#大阪公立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 7^{80}$の下5桁を求めよ.
大阪公立大過去問
この動画を見る
$ 7^{80}$の下5桁を求めよ.
大阪公立大過去問
2023高校入試解説5問目 2次方程式の応用 西大和学園

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$x^2 -ax + 1 = 0$の2つの解の差が$\frac{3}{2}$のときa=?
(a>0)
2023西大和学園高等学校
この動画を見る
2次方程式$x^2 -ax + 1 = 0$の2つの解の差が$\frac{3}{2}$のときa=?
(a>0)
2023西大和学園高等学校
ハルハルさんの作成問題「たぶん名作だと思います。難易度は高め」 図形 三角比

単元:
#数Ⅰ#数Ⅱ#式と証明#図形と計量#三角比への応用(正弦・余弦・面積)#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
この動画を見る
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
学習院大 二次不等式

単元:
#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=x^2+2(a-5)x+a^2-11a+26$
$f(x)a$を満たす実数xが存在するようなaの範囲を求めよ.
学習院大過去問
この動画を見る
$ f(x)=x^2+2(a-5)x+a^2-11a+26$
$f(x)a$を満たす実数xが存在するようなaの範囲を求めよ.
学習院大過去問
整式の剰余 2通りの解法で 中京大

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 3x^{3n+2}をx^2+x+1$で割った余りを求めよ.
中京大過去問
この動画を見る
$ 3x^{3n+2}をx^2+x+1$で割った余りを求めよ.
中京大過去問
福田の1.5倍速演習〜合格する重要問題054〜大阪大学2017年度文系第1問〜放物線とx軸で囲まれた面積

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ $b,c$を実数、$q$を正の実数とする。放物線$P:y=-x^2+bx+c$の頂点の$y$座標が
$q$のとき、放物線$P$と$x$軸で囲まれた部分の面積$S$を$q$を用いて表せ。
2017大阪大学文系過去問
この動画を見る
$\Large{\boxed{1}}$ $b,c$を実数、$q$を正の実数とする。放物線$P:y=-x^2+bx+c$の頂点の$y$座標が
$q$のとき、放物線$P$と$x$軸で囲まれた部分の面積$S$を$q$を用いて表せ。
2017大阪大学文系過去問
中学生が解くには難しい 平方根の計算 青山学院

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\frac{1}{2}(a^2 - \frac{1}{a^2})$
$\sqrt{1+x^2}$をaを用いて表せ。(a>0)
青山学院高等部
この動画を見る
$x=\frac{1}{2}(a^2 - \frac{1}{a^2})$
$\sqrt{1+x^2}$をaを用いて表せ。(a>0)
青山学院高等部
【数検2級】数学検定2級2次:問題1

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#2次関数#2次関数とグラフ#数学検定#数学検定2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.(選択)
aを定数とします。2次関数$y=2x^3-4ax+1(0\leqq x \leqq 3)$について、次の問いに答えなさい。
(1)$a=2$のとき、yのとり得る値の範囲を求めなさい。
(2)$y$のとり得る値の範囲が$1\leqq y\leqq 25$であるとき、aの値を求めなさい。
この動画を見る
問題1.(選択)
aを定数とします。2次関数$y=2x^3-4ax+1(0\leqq x \leqq 3)$について、次の問いに答えなさい。
(1)$a=2$のとき、yのとり得る値の範囲を求めなさい。
(2)$y$のとり得る値の範囲が$1\leqq y\leqq 25$であるとき、aの値を求めなさい。
因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x(y^3-z^3)+y(z^3-x^3)+z(x^3-y^3)$
これを因数分解せよ.
創価大過去問
この動画を見る
$ x(y^3-z^3)+y(z^3-x^3)+z(x^3-y^3)$
これを因数分解せよ.
創価大過去問
補助線のセンスを磨け!2通りで解説

西暦"2023"を含む入試予想問題(その4)~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$N$の整数部分が$ N=\sqrt{2023+x}$とする.
整数$x$はいくつあるか.
この動画を見る
$N$の整数部分が$ N=\sqrt{2023+x}$とする.
整数$x$はいくつあるか.
灘高校 因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a(x+2y)+b(x+3y)=-x+y$となるa,bを求めよ.
$x^2+5xy+6y^2-x+y+k$は$k=\Box$のとき,$\Box$と1次式×1次式に因数分解できる.
これを解け.
灘高校過去問
この動画を見る
$ a(x+2y)+b(x+3y)=-x+y$となるa,bを求めよ.
$x^2+5xy+6y^2-x+y+k$は$k=\Box$のとき,$\Box$と1次式×1次式に因数分解できる.
これを解け.
灘高校過去問
福田の1.5倍速演習〜合格する重要問題049〜早稲田大学2019年度商学部第2問〜折れ線の長さの最小値問題

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#微分法と積分法#点と直線#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
この動画を見る
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
東京電機大 最大値・最小値

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#三角関数#三角関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yを実数とする.
$x^2+2y^2+4y=0$を満たすとき,$2x-y$の最大値・最小値を求めよ.
東京電機大過去問
この動画を見る
x,yを実数とする.
$x^2+2y^2+4y=0$を満たすとき,$2x-y$の最大値・最小値を求めよ.
東京電機大過去問
ルートを外せ!!2023 受験生は概要欄を見よ

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{2023n}$が整数となる最小の整数n=?
この動画を見る
$\sqrt{2023n}$が整数となる最小の整数n=?
