 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
格子点を通るということは?【山口大学】【数学 入試問題】
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
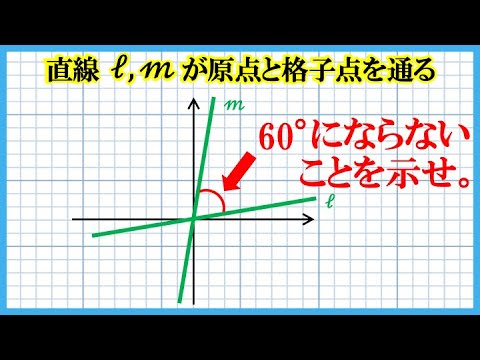
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
この動画を見る
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
【6分でマスター!!】単項式と多項式の次数の求め方を解説!(係数と定数項についても)〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
単項式と多項式の次数の求め方について解説します。
この動画を見る
数学1A
単項式と多項式の次数の求め方について解説します。
整数問題【一橋大学】【数学 入試問題】

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x$は0でない実数とする。$x-\dfrac{1}{x}$が0以外の整数ならば$x^2-\dfrac{1}{x^2}$は整数でないことを示せ。
一橋大過去問
この動画を見る
$x$は0でない実数とする。$x-\dfrac{1}{x}$が0以外の整数ならば$x^2-\dfrac{1}{x^2}$は整数でないことを示せ。
一橋大過去問
【数Ⅰ】2文字のたすき掛け【仕組みを理解して因数分解をしよう】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
(1) $ (2x+3)(3x+1)$を展開せよ.
(2) $ 6x^2+11x+3$ を因数分解せよ.
(3) $6x^2+2y^2+8xy+7x+y-3$を因数分解せよ.
この動画を見る
(1) $ (2x+3)(3x+1)$を展開せよ.
(2) $ 6x^2+11x+3$ を因数分解せよ.
(3) $6x^2+2y^2+8xy+7x+y-3$を因数分解せよ.
平方根と式の値

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y=4$ , $xy=2$ , $x-y>0$
$\frac{\sqrt x - \sqrt y }{\sqrt x + \sqrt y } =?$
県立広島女子大学
この動画を見る
$x+y=4$ , $xy=2$ , $x-y>0$
$\frac{\sqrt x - \sqrt y }{\sqrt x + \sqrt y } =?$
県立広島女子大学
二項定理を使ってあることに気付ける?【2017年一橋大学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#恒等式・等式・不等式の証明#数列#漸化式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
この動画を見る
$ P(0)=1,P(x+1)-P(x)=2x$を満たす整式$P(x)$を求めよ。
2017一橋大過去問
√と二乗
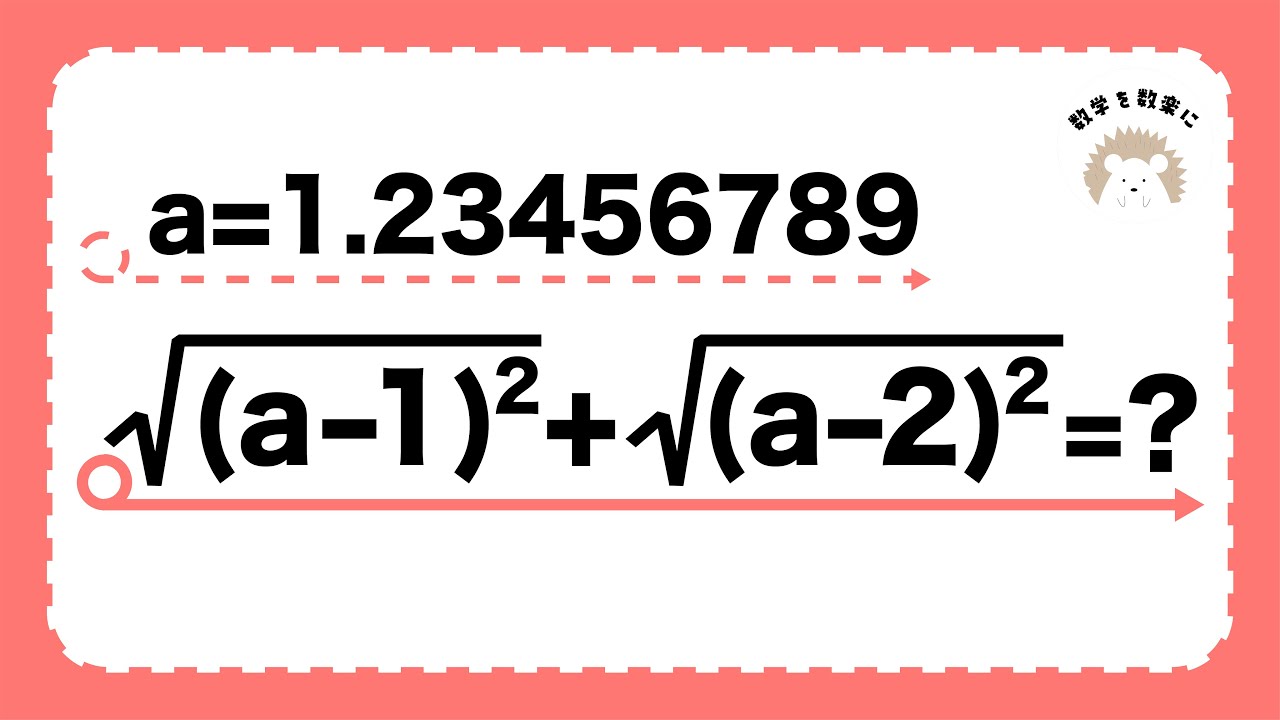
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a=1.23456789
$\sqrt{(a-1)^2} +\sqrt{(a-2)^2}=?$
この動画を見る
a=1.23456789
$\sqrt{(a-1)^2} +\sqrt{(a-2)^2}=?$
一文字削除からの判別式【2014年早稲田大学】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#式の計算(整式・展開・因数分解)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。
2014早稲田大過去問
この動画を見る
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。
2014早稲田大過去問
福田の数学〜一橋大学2022年文系第3問〜同値関係の証明と不等式の表す領域

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#一次不等式(不等式・絶対値のある方程式・不等式)#図形と方程式#恒等式・等式・不等式の証明#軌跡と領域#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の問いに答えよ。
(1)実数x,yについて、$「|x-y| \leqq x+y」$であることの必要十分条件は
「$x \geqq 0$かつ$y \geqq 0$ 」であることを示せ。
(2)次の不等式で定まるxy平面上の領域を図示せよ。
$|1+y-2x^2-y^2| \leqq 1-y-y^2$
2022一橋大学文系過去問
この動画を見る
次の問いに答えよ。
(1)実数x,yについて、$「|x-y| \leqq x+y」$であることの必要十分条件は
「$x \geqq 0$かつ$y \geqq 0$ 」であることを示せ。
(2)次の不等式で定まるxy平面上の領域を図示せよ。
$|1+y-2x^2-y^2| \leqq 1-y-y^2$
2022一橋大学文系過去問
対称式の良問【2008年早稲田大学】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$x$が$x^3+\dfrac{1}{x^3}=52$を満たすとき、$x^4+\dfrac{1}{x^4}$の値を求めよ。
2008早稲田大過去問
この動画を見る
実数$x$が$x^3+\dfrac{1}{x^3}=52$を満たすとき、$x^4+\dfrac{1}{x^4}$の値を求めよ。
2008早稲田大過去問
6乗−6乗 因数分解 京都産業大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^6-y^6$
京都産業大学
この動画を見る
因数分解せよ
$x^6-y^6$
京都産業大学
どっちがでかい?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$3^{\sqrt5}$ VS $5^{\sqrt3}$
この動画を見る
どちらが大きいか?
$3^{\sqrt5}$ VS $5^{\sqrt3}$
【次数が高くても焦るな】対称式 入試問題【2017年昭和大学】

単元:
#数Ⅰ#数Ⅱ#数と式#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a+b=1,a^2+b^2=3$のとき、$a^7+b^7$の値を求めよ。
2017昭和大過去問
この動画を見る
$a+b=1,a^2+b^2=3$のとき、$a^7+b^7$の値を求めよ。
2017昭和大過去問
因数分解(高校範囲)中学生も解けるやり方 高校生の解き方

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^4-4x^2+x+2$
北海道薬科大学
この動画を見る
因数分解せよ
$x^4-4x^2+x+2$
北海道薬科大学
福田の数学〜一橋大学2022年文系第2問〜平面上の三角形の面積の最大値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}\ 0 \leqq \theta \lt 2\pi$とする。
座標平面上の3点O(0,0), $P(\cos\theta,\sin\theta)$, $Q(1,3\sin2\theta)$
が三角形をなすとき、$\triangle OPQ$の面積の最大値を求めよ。
2022一橋大学文系過去問
この動画を見る
${\Large\boxed{2}}\ 0 \leqq \theta \lt 2\pi$とする。
座標平面上の3点O(0,0), $P(\cos\theta,\sin\theta)$, $Q(1,3\sin2\theta)$
が三角形をなすとき、$\triangle OPQ$の面積の最大値を求めよ。
2022一橋大学文系過去問
変な問題

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt{2\sqrt{4\sqrt{8\sqrt{16\sqrt{32\sqrt{\sqrt64・・・・・・・・}}}}}}$
これを解け.
この動画を見る
$ \sqrt{2\sqrt{4\sqrt{8\sqrt{16\sqrt{32\sqrt{\sqrt64・・・・・・・・}}}}}}$
これを解け.
【解けますよね?】対称式 入試問題【2013年横浜市大/改題】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a,b,c$を実数として、$A,B,C$を
$A=a+b+c$
$B=a^2+b^2+c^2$
$C=a^3+b^3+c^3$
とおく。この時$abc$を$A,B,C$を用いて表せ。
2013横浜市大改題過去問
この動画を見る
$a,b,c$を実数として、$A,B,C$を
$A=a+b+c$
$B=a^2+b^2+c^2$
$C=a^3+b^3+c^3$
とおく。この時$abc$を$A,B,C$を用いて表せ。
2013横浜市大改題過去問
【置き換え方を学ぶ!!】高校で出てくる展開(乗法の公式)と解き方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
展開(乗法の公式)と解き方について解説します。
$(2x-3y)^2$
$(3x+4y)(3x-4y)$
$(x-2)(x+3)$
$(a+b+c)^2$
$(3a+1)^2(3x-1)^2$
$(4x^2+y^2)(2x+y)(2x-y)$
この動画を見る
数学1A
展開(乗法の公式)と解き方について解説します。
$(2x-3y)^2$
$(3x+4y)(3x-4y)$
$(x-2)(x+3)$
$(a+b+c)^2$
$(3a+1)^2(3x-1)^2$
$(4x^2+y^2)(2x+y)(2x-y)$
中学生も解ける!?高校範囲の因数分解

中学生向け「どっちがでかい?」

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{10^{2021}+1}{10^{2022}+1}$ VS $ \dfrac{10^{2022}+1}{10^{2023}+1}$
どちらが大きいか?
この動画を見る
$ \dfrac{10^{2021}+1}{10^{2022}+1}$ VS $ \dfrac{10^{2022}+1}{10^{2023}+1}$
どちらが大きいか?
因数分解 東海大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x+y+1)(x+6y+1)+6y$
東海大学
この動画を見る
因数分解せよ
$(x+y+1)(x+6y+1)+6y$
東海大学
【#11】【因数分解100問】基礎から応用まで!(96)〜(100)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(96)$(x+y+z)(x+y-z)(x-y+z)(x-y-z)$
(97)$(a+b)(b+c)(c-a)(a-b+c)$
(98)$(c+ab)(d-ac+ab)$
(99)$3(c+d)(a+b+c)(a+b+d)$
(100)$(3a^2+b^2)(a^2+3b^2)$
この動画を見る
(96)$(x+y+z)(x+y-z)(x-y+z)(x-y-z)$
(97)$(a+b)(b+c)(c-a)(a-b+c)$
(98)$(c+ab)(d-ac+ab)$
(99)$3(c+d)(a+b+c)(a+b+d)$
(100)$(3a^2+b^2)(a^2+3b^2)$
【数学I/高1の予習】文字を含んだたすきがけの因数分解
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
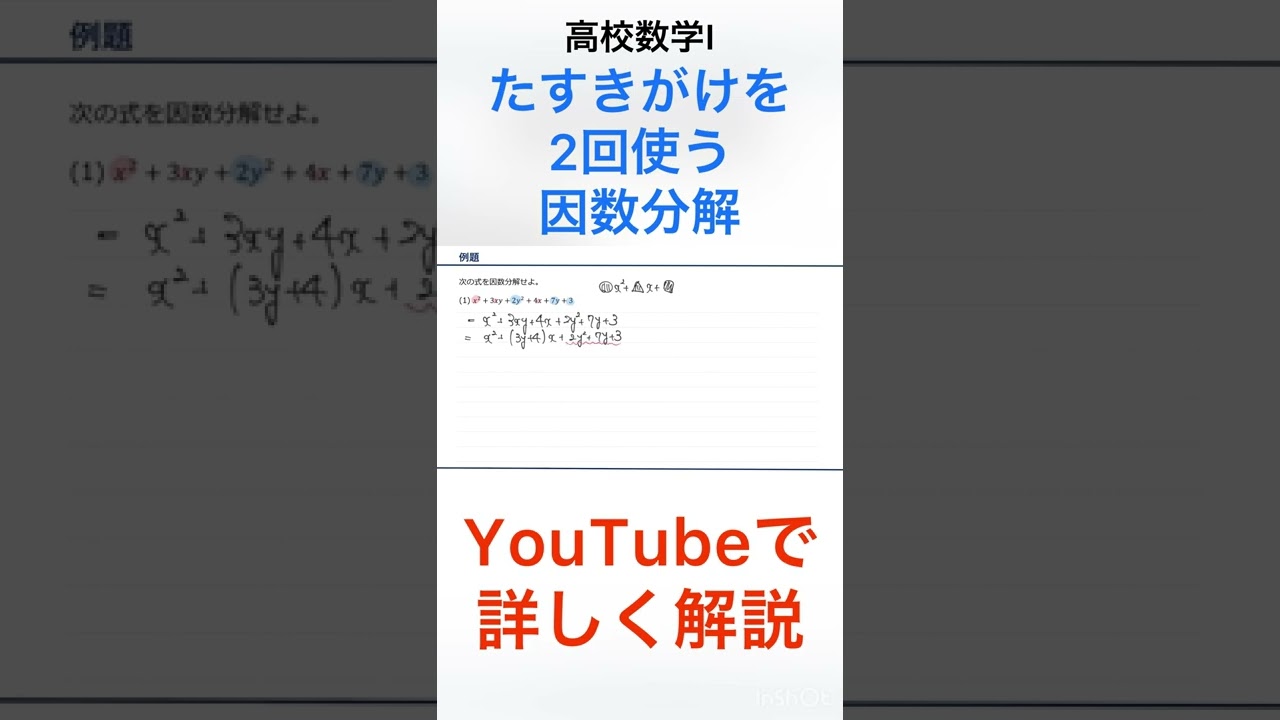
次の式を因数分解せよ
$x^2+3xy+2y^2+4x+7y+3$
この動画を見る
次の式を因数分解せよ
$x^2+3xy+2y^2+4x+7y+3$
【#10】【因数分解100問】基礎から応用まで!(91)〜(95)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(91)$(3x-8)(16x+9)$
(92)$(25x-16)(4x+5)$
(93)$3(a+b)(b+c)(c+a)$
(94)$24xyz$
(95)$(x+y+2)(x-y-2)(x+y-2)(x-y+2)$
この動画を見る
(91)$(3x-8)(16x+9)$
(92)$(25x-16)(4x+5)$
(93)$3(a+b)(b+c)(c+a)$
(94)$24xyz$
(95)$(x+y+2)(x-y-2)(x+y-2)(x-y+2)$
【#9】【因数分解100問】基礎から応用まで!(81)〜(90)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(81)$(x+1)(x^2+x+1)(x^2-x+1)$
(82)$(x+1)(x^2+1)(x^4+1)$
(83)$(a+b-1)(a-2b+c)$
(84)$(a-c)^3$
(85)$(x^2+2x-2)(x^2+2x-21)$
この動画を見る
(81)$(x+1)(x^2+x+1)(x^2-x+1)$
(82)$(x+1)(x^2+1)(x^4+1)$
(83)$(a+b-1)(a-2b+c)$
(84)$(a-c)^3$
(85)$(x^2+2x-2)(x^2+2x-21)$
すっきり、あっさり

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ z=1+\sqrt[5]{2}+\sqrt[5]{4}+\sqrt[5]{8}+\sqrt[5]{16}$である.
$ \left(1+\dfrac{1}{z}\right)^{50}$の値を求めよ.
この動画を見る
$ z=1+\sqrt[5]{2}+\sqrt[5]{4}+\sqrt[5]{8}+\sqrt[5]{16}$である.
$ \left(1+\dfrac{1}{z}\right)^{50}$の値を求めよ.
【#8】【因数分解100問】基礎から応用まで!(71)〜(80)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(76)$(2x-3y+1)(3x+2y-1)$
(77)$(3x-4y)^2$
(78)$(x-y-1)(x^2+y^2+1+xy+x-y)$
(79)$(x^2+4x+6)(x^2+8x+6)$
(80)$-3(2x-1)(x-3)(x+2)$
この動画を見る
(76)$(2x-3y+1)(3x+2y-1)$
(77)$(3x-4y)^2$
(78)$(x-y-1)(x^2+y^2+1+xy+x-y)$
(79)$(x^2+4x+6)(x^2+8x+6)$
(80)$-3(2x-1)(x-3)(x+2)$
!
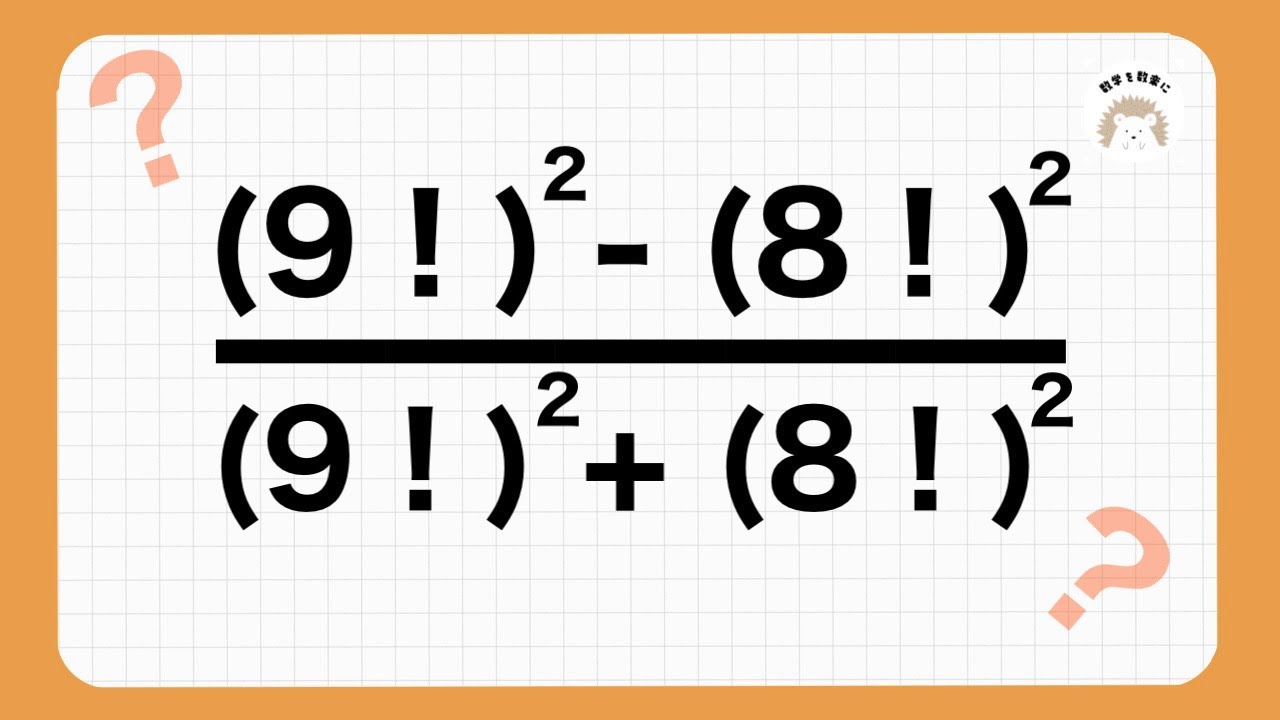
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(9!)^2 - (8!)^2} {(9!)^2 + (8!)^2} $
この動画を見る
$\frac{(9!)^2 - (8!)^2} {(9!)^2 + (8!)^2} $
【数学Ⅰ/高1の予習】たすきがけを使う因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を因数分解せよ
$6x^2+7x+2$
この動画を見る
次の式を因数分解せよ
$6x^2+7x+2$
【#7】【因数分解100問】基礎から応用まで!(61)〜(70)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(66)$a^3-b^3+6ab+8$
(67)$a^3-b^3-c^3-3abc$
(68)$x^3-8y^3+6xy+1$
(69)$a^5-a^2b^2(a-b)-b^5$
(70)$x(y^2-z^2)+y(z^2-x^2)+z(x^2-y^2)$
この動画を見る
(66)$a^3-b^3+6ab+8$
(67)$a^3-b^3-c^3-3abc$
(68)$x^3-8y^3+6xy+1$
(69)$a^5-a^2b^2(a-b)-b^5$
(70)$x(y^2-z^2)+y(z^2-x^2)+z(x^2-y^2)$
